基于风致响应计算的建筑玻璃幕墙应力检测方法
侯经文 孙登科


摘 要:基于风载荷作用,点支式建筑玻璃幕墙极易破损与脱落,对此需对其风致应力进行有效检测,以此文章提出了基于风致响应计算的建筑玻璃幕墙应力检测方法,以均风特性与脉动风特性为载体得知幕墙基本风压特性,基于风致响应计算与基本风压特性,获得建筑玻璃幕墙风振系数,以此得出风致应力,实现玻璃幕墙风致应力检测。并以Matlab仿真平台为载体,通过Linux操作系统测试了风致应力检测方法的实效性,结果表明,此方法检测时间短、效率高、准确率高,值得大力推广应用。
关键词:风致响应计算;建筑玻璃幕墙;应力检测
中图分类号:TU228 文献标识码:A 文章编号:1001-5922(2021)09-0120-04
Stress Detection Method of Building Glass Curtain Wall Based on Wind-induced Response Calculation
Hou Jingwen, Sun Dengke
(Shaanxi Polytechnic Institute, Xianyang 712000, China)
Abstract:Based on wind load, point-supported glass curtain wall is easy to break and fall off. For this, it needs to be effectively tested for wind-induced stress. In this paper, the wind-induced stress detection method based on wind-induced response calculation is proposed. The basic wind pressure characteristics of the curtain wall are obtained based on the uniform wind characteristics and the pulsating wind characteristics. Based on wind-induced response calculation and basic wind-pressure characteristics, the wind-induced vibration coefficient of the building glass curtain wall is obtained, and the wind-induced stress is obtained from this, and the wind-induced stress detection of the glass curtain wall is realized. With the Matlab simulation platform as the carrier, the effectiveness of wind induced stress detection method is tested by Linux operating system. The results show that the detection time is short, the efficiency is high, and the accuracy is high, so it is worth popularizing and applying.
Key words:wind-induced response calculation;building glass curtain wall;stress detection
0 引言
尽管当前风致建筑倒塌现象并未发生,但是受强风影响,建筑玻璃幕墙被损坏与脱落的现象屡见不鲜。陈怡然、马宁等学者基于FLU.ENT软件,并以湍流模型为载体进行了点支式建筑玻璃幕墙四周风场绕流仿真模拟,于不同风向角计算风载体型与风压系数,通过ANSYS软件建模,以数值模拟获取风载體型系数与风压具体时程,以实现建筑玻璃幕墙风致应力检测,但消耗时间过长,检测效率较低[1]。对此本文提出基于风致响应计算的建筑玻璃幕墙风致应力检测方法。
1 均风特性分析
1.1 风速剖面分析
均风速剖面为微气象学领域风速变化的关键方式,对数律与指数律比较常见[2]。
对数律主要表征大气底层强风风速轮廓线,效果良好,即:
其中,w(h1)代表大气底层内部高度h1位置的均风速;w1代表摩擦速度;k代表卡曼常数,一般选为0.4;h代表地面粗糙长度,单位为m;h1代表有效高度,单位为m,表达式即h1=h'-hc,h'代表离地高度,单位为m,hc代表零均位移,单位为m。
沿着高度不断变化,均风速可以通过指数函数加以表示,则:
其中,hd代表标准参考高度;wd代表标准参考高度位置的均风速;h'代表任何高度;w(h')代表任何高度位置的均风速;a代表地面粗糙度指数。
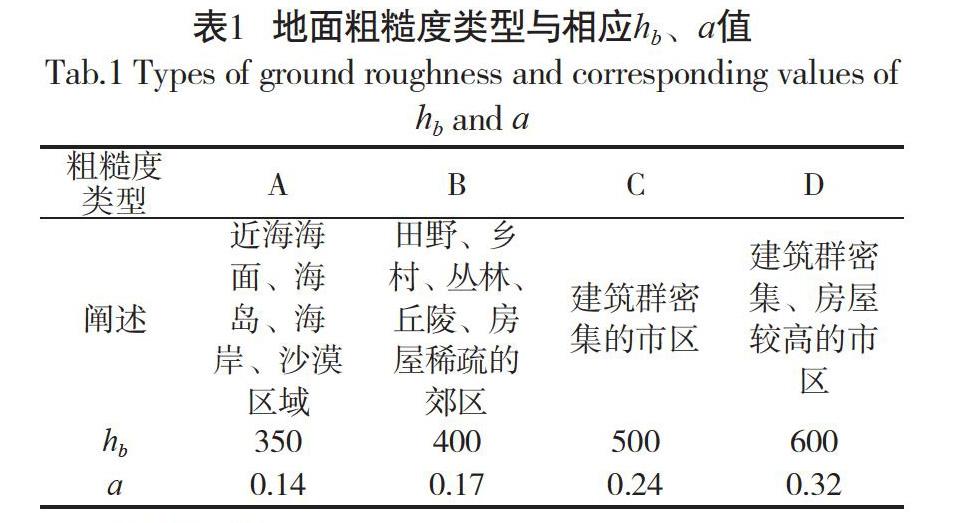
在工程实践中,由于指数律计算过于简单,并指数律与对数律存在差异并不显著,因此利用指数律加以计算分析。荷载规范明确指出4种不同类型粗糙度及其相应梯度风高度hb与对应指数a确定的风剖面。地面粗糙度类型与相应hb、a值具体如表1所示。
1.2 基础风速
基础风速就是基于标准要求,统计分析风速相关数据信息,所获最大均风速。载荷具体规定指出所谓标准要求即地面粗糙度B类,高度10m,重现期50年,风时距10min,概率分布函数类型属于极值Ⅰ型分布[3]。
一年作为一周期,以每年最大均风速为数理统计样本。就概率层面而言,间隔既定时间之后,会有大于年最大均风速的风速出现,即重现期。
重现期是t年基础风速,那么在任何年度,超越此风速一次性的概率是。所以不超出此基础风速的概率,即:
由此可知,重现期50年时,保证率为98%。而基础风压就是根据重现期所定义的。
通常来讲,研究对象并非存在异常现象的气候状态,即良态气候。良态气候选择极值Ⅰ型分布函数统计分析基础风速,即:
其中,α代表尺度参数;代表位置参数,可基于下式获取,即:
其中,i'代表数学期望;σi代表根方差,可通过数理统计获得。通过公式(4)转换,可以得出,即:
其中,代表基础风速,代表小于基础风速的概率,与重现期的关系,即:
根据重现期内含,代表大于基础风速的概率,1-代表小于等于此基础风速的概率。
在公式(6)中代入α与,便可得到,即:
其中,i1代表设计最大风速,即基础风速;γ代表保证系数,表达式即:
1.3 基础风压
实测记录为风速,而在实践中需通过风压进行计算分析,这就需要转变风速为风压[4]。基于流体定常设定,在任何流线的任何点的伯努利方程,即:
其中,N'代表单位面积静压力,单位为kN/m2;ρ代表空气密度,单位为t/m3;w'代表沿某流线的风速,单位为m/s;代表动压。
在风速为0的时候,G=N''即最大静压力;设定N=N''-N',那么即净压力,通过公式(10)获得,即:
通过公式(11),便可把基础风速(w0/i1)转变为基本风压N0,则:
2 脉动风特性分析
所谓湍流强度即大气湍流度最为简洁的相关参数,可以于3个正交方向瞬时风速风量独立明确,然而大气边界层纵向分量相对较大[5],因此以纵向脉动风湍流强度为例,即:
其中,I(h)代表h高度位置的湍流强度;σw'f (h)代表顺风向脉动风速根方差;w(h)代表高度h位置的均风速。
高度越高,脉动风速根方差越小,均风速越大,相关规范明确了I(h)表达式,即:
其中,I10代表高度为10m时的名义湍流度,相应的4种不同地貌取值即0.14、0.16、0.25、0.41。
基于脉动风速功率谱长期研究分析,相关专家提出了各种模式的多风速谱密度相应函数方程式,最为著名的便是达文波特风速谱[6],即:
其中,uDw' (u)表示功率谱;u表示风频率;w10表示标准均风速;k表示粗糙度系数。
3 风致应力响应计算方法
基于均风特性与脉动风特性分析,以获得点支式建筑玻璃幕墙四周风的具体特性,据此检测玻璃幕墙风致应力[7]。风致应力检测算法具体步骤即:
就多自由度体系的m个自由度结构,可以矩阵阐述运动微分表达式,即:
其中,Z表示质量矩阵;j''(t)表示结构节点加速度向量;G表示阻尼矩阵;j'(t)表示结构节点速度向量;R表示刚度矩阵;j(t)表示结构节点位移向量;Q表示荷载分布矩阵;p(t)表示多维节点脉动风向量。
设定为前n阶模态矩阵,基于振型分解模式展开位移,即:
通过瑞雷阻尼假设公式(17)与公式(18)相结合,振型对于高度、质量分布可直接满足正交性要求,运动方程可以选择振型广义坐标加以表征。
基于脉动风载荷,每次进行测量时,即使处于相同条件,振动过程都会存在一定差异,以上具备不明确性与非重现的风载荷,属于随机荷载,受随机荷载作用结构振动呈现为随机性振动。
假设Kffk表示脉动风抖振力互谱,则:
其中,表示随机脉动风检测时的功率谱矩阵。
假设表示抖振力互谱矩阵,则:
对应谱与载荷谱的关系基于随机振动理论,可通过传递函数加以描述,以获取位移移动功率谱Kqxqk(u),则:
假设表示功率谱矩阵形式,则:
其中,表示传递函数矩阵。
基于公式(18)把通过公式(22)计算获得的位移功率谱进行振型组合处理分析,以获取动力位移功率谱矩阵,即:
假设Kj(u)表示功率谱矩阵形式,则:
公式(23)与公式(24)包含所有振型交叉项。
假設表示动力位移根方差,基于谱密度积分获取,一般根方差所阐述的是均方幅值。假设jx表示第x点动力位移响应值,则:
假设Lfx表示第x点等效惯性力,一般都是通过脉动风引发,则:
其中,ny表示节点质量;vx表示x第阶频率; 表示第x阶振型。
基于公式(26)获得静力等效风荷载,即:
假设λy表示风荷载风振系数,则:
第y阶振型风载荷生成应力计算公式即:
就公式(29)实现点支式建筑玻璃幕墙风致应力检测。
4 仿真分析
以Matlab仿真平台为载体,基于Linux操作系统,测试风致应力检测算法的实效性。检测效率为主要指标,根据风致应力检测所消耗时间分析检测效率,测试结果具体如图1所示。
由图1可以看出,点支式建筑玻璃幕墙风致应力检测算法在进行风致应力检测的时候,于多次迭代中所耗费时间较少,可有效控制在4s以内,这主要是由于检测风致应力前,对均风特性与脉动风特性进行了深入分析,以此为风致应力检测奠定了有力基础,减少了检测时间,提升了检测效率。
风致应力检测算法的准确率测试结果具体如图2所示。
由图2可以看出,风致应力检测算法于多次迭代中整体准确率都保持在85%~95%之间,准确率非常高,这主要是由于风致应力检测算法基于风致响应计算以结构参振模态数为载体获取了幕墙风致应力,保障了较高检测准确率[8]。
5 结论
总而言之,在轻质高强材料广泛应用趋势下,建筑开始朝向于高、柔方向发展,导致结构频率下降,逐步与风频率相接近,使得一些建筑玻璃幕墙受强风载荷影响严重损坏,直接威胁社会公众安全。因此为保障人们的生命财产安全,对建筑玻璃幕墙进行风致应力检测具有重要意义。而目前玻璃幕墙风致应力检测算法效率与准确率不高现象突出,因此提出了基于风致响应计算的点支式建筑玻璃幕墙风致应力检测算法。并通过Matlab仿真平台,以及Linux操作系统测试了风致应力检测方法的实效性,结果表明,此方法检测时间短、效率高、准确率高。
参考文献
[1]杨明.高层建筑风荷载及风致响应研究[D].长沙:湖南大学,2013.
[2]刘冰.基于改进SFLA的高层建筑幕墙风振可靠性研究[D].邯郸:河北工程大学,2015.
[3]李万润,刘宇飞,方钊.考虑残余应力的高层钢框架梁柱节点焊缝风致疲劳评估[J].东南大学学报(自然科学版),2019,49(4):672-678.
[4]王腾飞,邹良浩,孙艳.高层住宅建筑风荷载特性及风致响应[J].土木工程与管理学报,2018,35(4):164-168+198.
[5]方钊,李爱群,李万润.高层钢框架支撑结构多尺度风致疲劳分析方法[J].东南大学学报(自然科学版),2017,47(1):137-141.
[6]郅伦海,余攀.基于卡尔曼滤波的高层建筑风荷载反演研究[J].武汉理工大学学报,2016,38(2):57-63+81.
[7]龚洁.点支式建筑玻璃幕墙风致应力检测算法仿真[J].计算机仿真,2019,36(11):356-359+395.
[8]冯畅达.超高层建筑风荷载和风致响应的吹气控制研究[D].黑龙江:哈尔滨工业大学,2014.

