基于ABAQUS的微细电火花超声振动主轴仿真研究∗
姚振扬 张家远 刘 明 张勤河
(1 中国航空工业集团公司北京长城计量测试技术研究所 动密封研究与工程技术中心 北京 100095)
(2 山东大学机械工程学院 山东大学高效洁净机械制造教育部重点试验室 机械工程国家级实验教学示范中心 济南 250061)
0 引言
电火花加工技术(Electrical discharge machining,EDM)是利用电极和工件放电产生的高温、高压来加工材料,广泛应用于航空航天、医疗器械等领域[1−3]。微细电火花技术(MicroEDM)是以电火花加工技术为基础发展的新型加工技术,利用微细工具电极和工件之间的微小脉冲放电去除多余的金属,常被用于微细轴、微细孔以及微细槽等三维结构的加工[4−6],但加工效率和加工精度较低。
超声振动辅助微细电火花加工技术是一种新型的微细电火花技术,将超声波加工技术与微细电火花加工技术进行优势互补,提升了工作介质的消电离能力,避免了非正常放电现象的发生,增加了加工过程中的有效放电次数,促进了电蚀产物的排出,加工效率和加工精度明显提高[7−10]。作为超声振动辅助微细电火花加工的核心部件,超声振动主轴设计的好坏直接决定了最终的加工效果,如果采用传统设计方式,会大幅提升研发周期和成本,往往还得不到最优的效果,因此,利用仿真软件对超声振动主轴进行研究具有重要的意义[11−14]。
已知设计的超声振动主轴模型如图1所示。超声振动主轴主要由后端盖、压电陶瓷、绝缘垫片、变幅杆、紧固螺栓、SK10 夹头和工具电极等组成。为确保超声振动主轴结构更加紧凑,减少谐振时连接面的阻抗,换能器长度取1/4 波长,直径为38 mm,长度为56 mm;第一级变幅杆直径分别为38 mm和25 mm,长度分别为4 mm 和109 mm,过渡圆弧半径为12.5 mm;第二级变幅杆直径为18 mm,长度为56 mm,过渡圆弧半径为3 mm。

图1 超声振动主轴的结构示意图Fig.1 Structure diagram of ultrasonic vibration spindle
1 超声振动主轴的模态分析
模态分析主要研究超声振动主轴在外部振动激励下的动态特性,从而分析激励过程中的动态响应。模态分析的过程其实就是基于线性系统运动微分方程来求解结构无阻尼自由振动问题,运动微分方程可以表示为
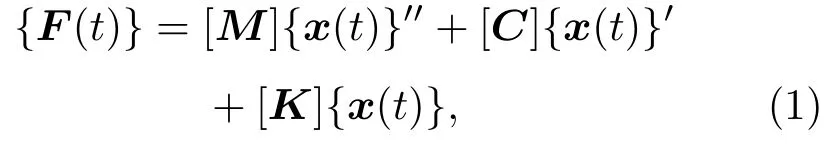
式(1)中,{F(t)}为外部激励的力向量;[M]为系统质量矩阵;{x(t)} 为位移响应向量;[C]为系统阻尼矩阵;[K]为系统刚度矩阵。
在有限元分析时,超声振动主轴为自由振动,此时运动微分方程简化为

引入简谐振动求解其统各阶模态的固有频率和振型,求解过程可以表示为

式(3)中,{x(t)}为位移响应向量;{g}为振幅列向量;ω为超声振动主轴固有频率。
将公式(3)代入公式(2)中,可得

求解公式(4),可得到其固有频率ω2和超声振动主轴自由振动下的各阶振型{g}。
基于以上模态分析的基本理论,对超声振动主轴模型开展模态分析。首先,运用SolidWorks 2016软件对其进行建模,将其转换成xt格式后导入ABAQUS 2016 中进行分析;其次,对其各部分的材料进行定义,后端盖采用铝合金材料,紧固螺栓采用40Cr 材料,绝缘垫片采用橡胶材料,压电陶瓷采用PZT-8 材料,超声波变幅杆采用钛合金材料,各部分材料物理参数如表1所示;再次,对其进行网格划分,选用正四面体结构均匀划分,划分后的网格如图2所示,共计划分37302个单元和59054个节点;最后,在节面处添加固定约束,开始模态分析的计算。

图2 超声振动主轴网格划分示意图Fig.2 Schematic diagram of grid generation for ultrasonic vibration spindle
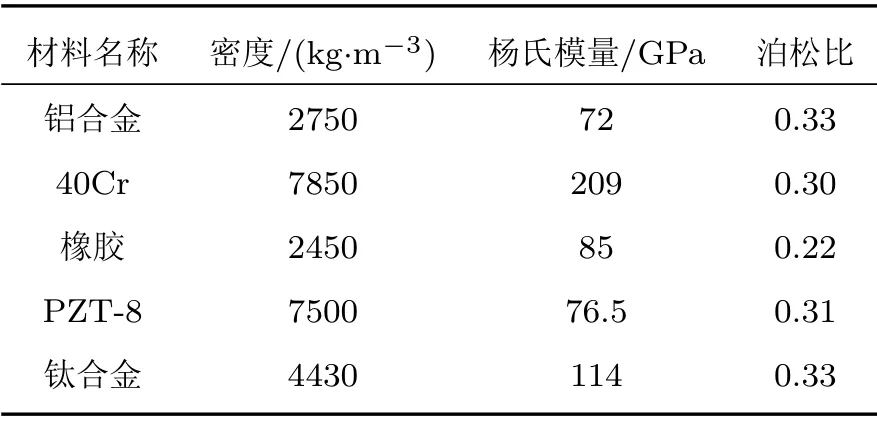
表1 各部分材料的物理参数Table 1 Physical parameters of the material
已知本文使用的超声振动主轴模型的理论谐振频率为27 kHz,因此,分别选取第19阶、第20阶、第21 阶、第22 阶和第23 阶等5 阶振型进行分析,超声振动主轴各阶振型的变形情况如图3所示,各阶的谐振频率如表2所示。由选取的5 个振型变形情况可知,第21 阶模态的变形比较均匀,其谐振频率与理论值误差仅为1.1%。

表2 超声振动主轴模态分析各阶固有频率Table 2 Modal analysis of ultrasonic vibration spindle

图3 超声振动主轴各阶模态Fig.3 Modes of ultrasonic vibration spindle
2 超声振动主轴的谐响应分析
谐响应分析主要为了得到最大响应位移和振幅放大系数等,通过分析周期载荷持续作用在线性结构系统时产生的持续周期响应,确定系统受到正弦载荷时的稳态响应,从而通过变化规律了解系统的工作性能。
系统在简谐载荷作用下的受迫振动方程为

式(5)中,[C]为阻尼矩阵;{F}为简谐载荷的幅值向量;θ为激振力的频率,单位Hz。其稳态响应可以表示为
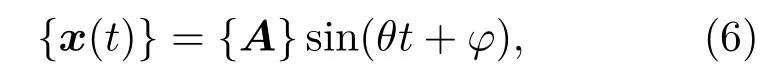
式(6)中,{A}为位移幅值向量,与系统固有频率ω、激振力频率θ和阻尼[C]有关;φ为位移响应滞后激振力的相位角,单位rad。
基于以上谐响应分析的基本理论,对超声振动主轴开展谐响应分析,为减少工作量,扫频范围为24~30 kHz,临界阻尼系数设置为0.01,在后端盖施加指向末端的1.6 MPa 压强,仿真结果如图4和图5所示。由图4可知,频率在26.727 kHz时端面振幅和相位角斜率最大,此时输出端与输入端最大比值为4.22,其理论变幅比为4.46,仿真值与理论值误差仅为5.38%;由图5可知,在频率26.727 kHz时,端面输出位移最大,最大值为6.761 µm,并且此时,节点处应力最大,因此,满足设计要求。

图4 超声振动主轴的频率响应Fig.4 Frequency response of ultrasonic vibration spindle

图5 超声振动主轴的位移云图和应力云图Fig.5 Displacement and stress nephogram of ultrasonic vibration spindle
3 超声振动主轴的实验测试
3.1 阻抗分析
将设计的超声振动主轴进行机械加工,加工后的超声振动主轴如图6所示。使用阻抗分析仪对超声振动主轴进行测试,阻抗分析仪测试结果如图7所示,导纳圆图无寄生圆,振动系统设计合理,振动性能稳定。谐振频率与理论值误差仅为0.34%,与仿真结果误差仅为0.37%,在误差允许范围内。

图6 加工后的超声振动主轴Fig.6 Ultrasonic vibration spindle after machining

图7 阻抗分析仪测试结果Fig.7 Test results of impedance analyzer
3.2 幅值测试
使用如图8所示的超声振幅测量仪对加工的超声振动主轴进行测试,仪测量结果如表3所示,振幅范围2~6 µm,最大振幅与仿真结果相差不大,满足设计要求。

图8 使用的超声振幅测量仪Fig.8 Ultrasonic amplitude measuring instrument
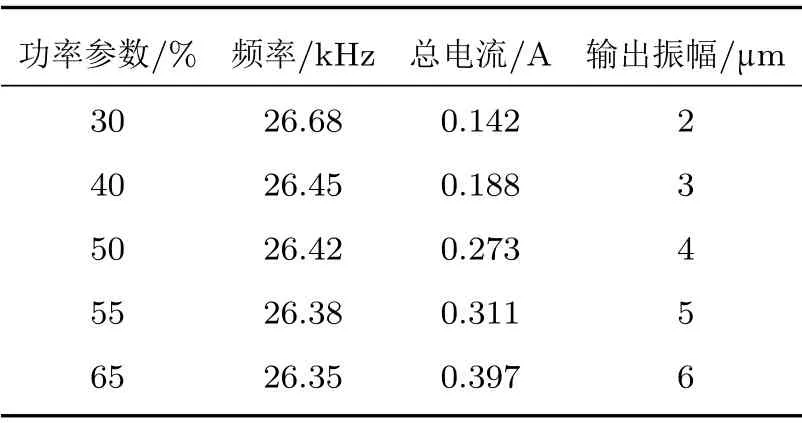
表3 超声振幅测量仪测量结果Table 3 Measurement results of ultrasonic amplitude meter
4 结论
本文对设计的微细电火花超声振动主轴进行了仿真研究。基于模态分析的基本理论,对超声振动主轴进行了模态分析,得到了各阶模态振型的变形情况和谐振频率,最终确定第21阶振型为所需振型。基于谐响应分析的基本理论,对超声振动主轴进行了谐响应分析,得到了各阶模态振型的振幅频率响应、相位频率响应、位移云图和应力云图。对加工出来的超声振动主轴进行阻抗分析和幅值测试,测试结果与仿真结果基本一致。

