压缩感知在宽带声学多普勒测速技术中的应用∗
刘舒宁 邓 锴 王长红
(1 中国科学院大学 北京 100049)
(2 中国科学院声学研究所 北京 100190)
(3 北京市海洋声学装备工程技术研究中心 北京 100190)
0 引言
宽带多普勒测速采用模拟方式处理宽带回波信号,在模拟域进行混频处理很难保证混频信号的绝对正交,因此会产生相频失真。若直接对回波信号以奈奎斯特速率采样将信号从模拟域转化到数字域处理,则对A/D要求高,在硬件上难以实现。一种解决方法是对宽带回波信号进行带通采样[1],由信号的中心频率与带宽决定采样频率。文献[2]指出,对于高频信号来说,要想获得较高的信号采样量化信噪比,带通采样频率宜尽可能选高一些。文献[3–4]也指出,对于高频宽带信号,带通采样的采样率以及采样后的数据量依然非常高,并提出了利用压缩感知理论对信号以低采样率进行采样、低数据量进行存储的方法。目前宽带信号处理存在的所需采样率高和数据存储空间大的问题,其根本原因在于传统采样的采样率是由信号的频率和带宽决定的。压缩感知(Compressed sensing,CS)[5−7]作为一种新的信号采样方式,可突破均匀采样的限制实现信息采样,即由信号中所含有用信息来决定其采样的数据量,从而减少需采样数据量,提高采样效率。压缩感知在水声领域常被应用于水声信号的压缩重构、水声信道估计等研究中[8−9]。
本文将压缩感知应用于声学多普勒测流测速,对利用压缩感知理论处理宽带回波信号的性能进行研究。利用点回波宽带测频模型[10]设计回波信号,对高采样率离散化后的回波信号数据进行压缩感知观测采样和重构,并比较回波信号在不同的稀疏基和观测矩阵下的信号重构精度,在此基础上选择合适的重构参数。利用复协方差法估计多普勒频移[11−15],分析压缩感知方式处理回波信号的频移偏差结果。另外,对带通采样与压缩感知两种回波信号处理方法进行对比,在相同噪声条件下分别利用两种方法对信号进行处理,对频移误差结果进行对比分析。仿真实验结果表明,在无噪声的理想条件下,利用压缩感知理论处理宽带多普勒测速的回波信号,相对频移偏差小于0.1%;在相同的噪声条件下,应用压缩感知方法处理后的回波信号能够获得与带通采样方法相当的测频性能,符合宽带声学多普勒测速的精度要求。
1 压缩感知基本原理
假设一维回波信号x ∈CN×1可以用一组基ΨT=[ψ1,ψ2,···,ψn,···,ψN]线性表示为

其中:α是N ×1 的系数向量,Ψ是N ×N矩阵,αn=〈x,ψn〉。
若向量α中的非零元素个数K ≪N,则信号α在基Ψ上是稀疏的。将稀疏信号x中的信息用一组观测向量ΦT=[φ1,φ2,···,φm,···,φM]进行观测得到观测值ym=〈x,φTm〉,即

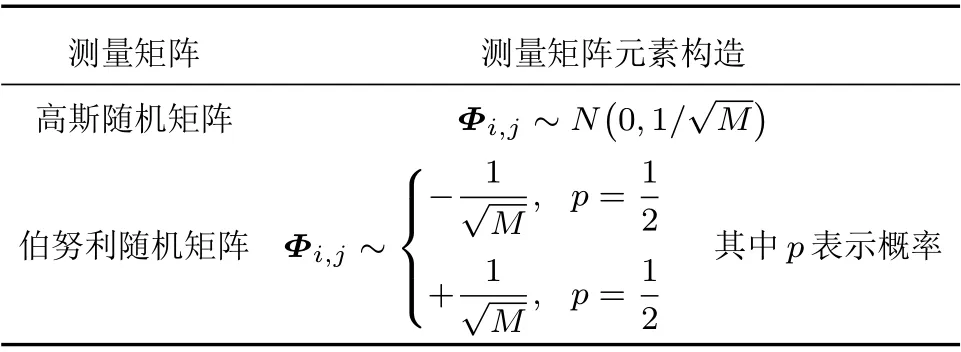
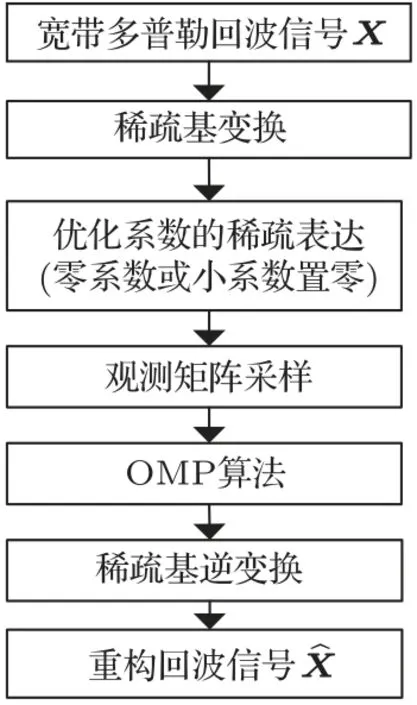
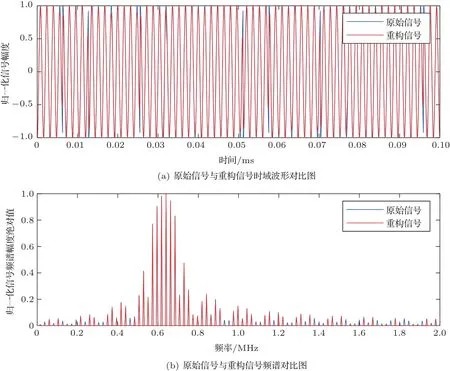
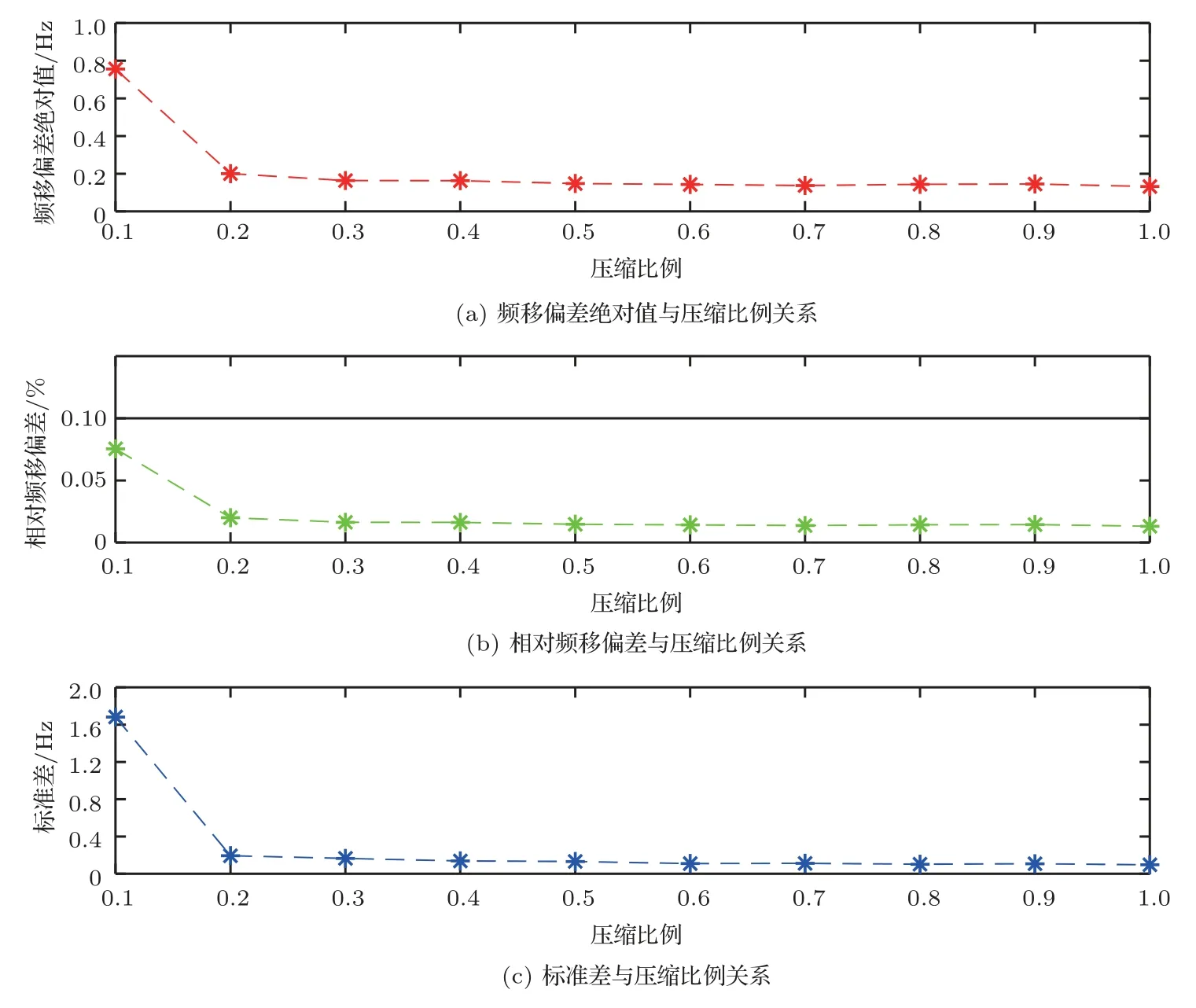
其中:原始信号x为N ×1 矩阵,观测值y为M ×1矩阵,Φ为M ×N的观测矩阵且M 结合式(1),得 其中:Θ=ΦΨ,Θ是M ×N矩阵。 由于M 利用观测值对信号进行重构本质是求解式(5)的l0范数最优化问题得到α,通过α恢复原始信号: 由于式(5)的求解是NP-hard 问题(在多项式时间内难以求解且无法验证该解是否可靠),研究表明,可将求解l0最小范数转化为求解l1最小范数,修改约束条件后重构问题转变为式(6)可求解的凸优化问题[17]: 由压缩感知基本原理可知,在宽带多普勒测速技术中应用压缩感知处理回波信号重点为回波信号的稀疏分解、测量矩阵的选择以及信号重构。 由式(1)可知,理想条件下,若系数向量α中的非零值的个数较少,则认为信号在基向量Ψ上是稀疏的。在实际应用中,若系数向量α中包含了少量大系数以及大量小系数,则通过适当的准则舍弃小系数(用0 替代),保留大系数来实现信号的稀疏表示,即在可接受的失真范围内找到信号的最简洁表示。 将宽带回波信号模型简化为[18] 其中,Y(t)是回波信号,X(t)是发射信号,σ(t)为信号从发射点至散射体和散射体至接收点的双程系统响应函数,暂不考虑散射体对回波信号的散射特性。 对回波信号进行离散化处理,令t=k1n,τ=k2m(假设m、n是和t、τ相关的离散时间变量),则,式(7)可以表示为 假设发射信号以及回波信号长度均为N,则离散化的卷积形式可以看作矩阵X和向量σ的乘积: 由式(9)可以看出,若将矩阵X看作某种稀疏基,则σ(n)是Y(n)在此稀疏基下的稀疏表示向量。本文选择常见的离散余弦变换基和离散傅里叶变换基作为稀疏基对回波信号进行稀疏分解,稀疏基矩阵元素构造如表1所示,并在仿真实验中对两种稀疏基下的稀疏分解性能进行对比。 表1 稀疏基表示Table 1 The structure of sparse bases 对信号进行稀疏表示后,在满足有限等距性质特性的前提下选择最优观测矩阵对回波信号进行观测得到重构回波信号所需的测量值。高斯随机矩阵和伯努利随机矩阵作为常用的测量矩阵,除易于构造外,最大优势在于与多数稀疏基(包含2.1 中介绍的离散傅里叶变换基和离散余弦变换基)都不相关[6],可以很好满足有限等距性质,所以本文选择高斯随机矩阵和伯努利随机矩阵作为观测矩阵,测量矩阵元素构造如表2所示,并比较不同测量矩阵下信号的重构效果。 表2 测量矩阵构造Table 2 The structure of measurement matrices 本文选择正交匹配追踪(Orthogonal matching pursuit,OMP)[19−20]算法作为重构算法对信号进行重构。OMP 算法的本质是以贪婪迭代思想在一定误差范围内寻找原始信号的最佳近似值来逼近和精确重构原始信号,方法是在每次循环迭代流程中从感知矩阵Θ中选择与观测值y最大程度相关的列向量并记录此列向量在感知矩阵Θ中的指向索引值,再从观测值y中减去相关部分后继续进行迭代流程,直至达到预先设定的迭代次数K或收敛后停止。算法流程如表3所示。 表3 OMP 算法流程Table 3 The algorithm flow of orthogonal matching pursuit 图1 回波信号的压缩感知与重构框图Fig.1 Block diagram of compressed sensing and reconstruction of echo signal 声学多普勒测速的基本原理[11−12]为:频率为f0的声波信号在水体中传播并经水中散射体反射后传播至换能器接收得到回波信号,处理计算得到回波信号频率为fr。根据多普勒频移原理,如果声源、散射体或水体间有相对速度,则f0与fr不相等,其差值fd为 其中:v为载体速度,c为声波在水中的传播速度,φ为载体运动方向与换能器发射波束声轴方向的夹角。 由式(10)可知,通过测量回波信号的多普勒频移可间接求出水流速度,目前在宽带声学多普勒测速中应用最广泛的频移测量处理算法是复协方差算法[11−15],其具有简单高效且实时性好的优点。多普勒频移测量精度决定速度测量的精度,因此对测速结果的误差分析可以简化为测频误差分析,回波信号的处理方法影响着频移测量的准确性。利用压缩感知理论处理回波信号并计算频移流程示意图如图2所示。 图2 压缩感知理论处理回波信号并计算频移流程示意图Fig.2 Schematic diagram of processing echo signal and calculating frequency shift by using compressed sensing theory 宽带声学多普勒测速设备发射信号一般采用伪随机编码序列调制后的余弦信号,本文首先在无噪声干扰情况下进行原理性验证实验,不考虑波束开角,基于复协方差法的点回波宽带测频模型设计宽带回波信号,假设得到无噪声干扰的理想原始回波信号为s(t)= cos(2π(f0+fd)t+ϕ(t)),其中参数设置为:采样频率fs= 20 MHz,中心频率f0= 624 kHz,编码序列[0,1,0,0,1,1,1],编码信号码元数L= 7,一次编码的发射脉冲宽度为896 µs,填充系数Q=4。假设回波信号中心频率f0对应的多普勒频移fd=1000 Hz。 为比较原始回波信号在不同稀疏基和观测矩阵下使用OMP 算法的信号重构效果,分别选择高斯随机矩阵和伯努利随机矩阵为观测矩阵,离散傅里叶变换基和离散余弦变换基作为变换基。信号重构质量的衡量标准为相关系数,表示为 其中,X为原始信号,为重构信号。 参数设置压缩比例为M/N(N为原始信号长度,M为观测后信号长度,M/N在[0,1]内取值),迭代次数设置K= 100。考虑到实验的随机性,对每次仿真过程重复100 次取平均值,仿真实验结果如图3所示。 图3 两种测量矩阵下原始回波信号与重构回波信号相关系数随压缩比例变化关系图Fig.3 Relationship diagram of correlation coefficient between original signal and reconstructed signal with compression ratio under two measurement matrices 从上述实验结果可以看出,使用离散傅里叶变换基的重构信号与原始信号相关性明显优于离散余弦变换基。为比较观测矩阵分别为高斯随机矩阵和伯努利随机矩阵时的重构效果,在不同变换基下分别使用两种观测矩阵对信号进行观测,由图3可知,在离散傅里叶变换基下,使用两种观测矩阵重构信号与原始信号的相关系数整体变化趋势为随着压缩比例的增加而增加,即信号的相关性随着压缩比例增加而提高。当压缩比例大于0.2时,相关系数变化趋于稳定并且两种观测矩阵下的相关系数差异不明显。压缩比例比较小时,使用高斯随机矩阵的信号相关系数略大于伯努利随机矩阵,随着压缩比例提高,使用两种观测矩阵下的信号相关系数相当且趋于稳定。因此,在下一步仿真实验中,选择离散傅里叶基作为变换基和高斯随机矩阵作为观测矩阵。 当压缩比例为0.4 时,选择高斯随机矩阵和离散傅里叶变换基,使用OMP 算法得到重构信号与原始信号时域和频域对比如图4所示。此时,重构回波信号与原始回波信号的相关系数大于0.98,重构回波信号与原始信号具有很好的相关性。 图4 原始回波信号与重构回波信号时域和频域对比图Fig.4 Comparison of original signal and reconstructed signal in time domain and frequency domain 为验证不同压缩比例下重构效果对频移计算的影响,利用复协方差法计算重构回波信号频移。按照2.4 节图2所示信号解调、低通滤波、实复变换、复自相关、频移求解过程对重构回波信号进行处理,考虑实验随机性,每个压缩比例下实验重复100 次,对计算结果取均值。多普勒频移偏差定义为∆f=(其中,为估计多普勒频移均值,fd为真实多普勒频移值);相对频移偏差定义为∆f/fd×100%;测量标准差定义为 对回波信号进行处理所得相对测频偏差和标准差与压缩比例关系如图5(a)所示,压缩比例大于0.2 时,频移偏差绝对值小于0.2 Hz,之后随压缩比例提高变化不大,此时对应图5(b)相对频移偏差小于0.02%。图5(c)显示实验标准差总体随压缩比例的上升而下降,且当压缩比例大于0.2 后变化不大。信号处理中残差产生的原因是利用OMP 算法对信号进行重构并不是对信号的精确重构,而是以贪婪迭代思想在一定误差范围内寻找原始信号的最佳近似值来逼近原始信号。结合图3相关系数与压缩比例关系可看出,重构误差对频移计算结果造成的影响处于较小范围内。 图5 频移偏差绝对值、相对频移偏差和标准差与压缩比例关系Fig.5 Relationship between absolute value of frequency shift deviation,relative frequency shift deviation and standard deviation and compression ratio 当回波信号含有噪声时,同样应用压缩感知理论对回波信号进行处理,并用OMP 算法对信号进行重构。并且为了对压缩感知与带通采样两种方法的回波信号处理效果进行比较,在同一段回波信号内加入与信号频带相同带宽的噪声后,分别用两种回波信号处理方法对回波信号进行处理。基于信号采样方式不同,在信号采样数据率相同的条件下,即使压缩感知压缩采样后的数据量与带通采样对回波信号采样后数据量一致,分别利用压缩感知方法和带通采样方法对不同信噪比条件下的回波信号进行处理。频移计算结果相对频移偏差与标准差如图6所示。 由图6看出,在0~30 dB不同信噪比条件下,基于压缩感知方法与带通采样方法处理宽带回波信号在频移计算结果上有相似的规律,随着信噪比提高,相对频移偏差与标准差逐渐降低,在达到一定信噪比后趋于稳定。整体来看,在低信噪比条件下,分别应用两种方法处理的回波信号相对频移偏差低于1%,应用压缩感知方法的相对频移偏差略小但差距不明显。在高信噪比条件下,分别应用两种方法处理的回波信号相对频移偏差低于0.1%,能够达到较好测频效果。综合图6误差分析,在相同的仿真条件下,分别应用压缩感知与带通采样两种方法对回波信号进行处理的频移计算结果无明显差异,两种方法下测频效果相当。 图6 不同信噪比条件下相对频移偏差与标准差Fig.6 Relative frequency shift deviation and standard deviation under different SNR conditions 综合以上实验分析,在不考虑波束开角、基于复协方差法的点回波宽带测频模型下,应用压缩感知方法处理无噪声理想回波信号的相对频移偏差小于0.1%,可达到较理想测频效果。对具有噪声干扰的0~30 dB 宽带多普勒回波信号,对比带通采样方法和压缩感知方法处理宽带回波信号的频移计算结果可知,应用两种方法处理回波信号的测频效果相当,满足宽带声学多普勒测速的精度要求。 本文将压缩感知重构信号理论应用于宽带多普勒测速的回波信号处理,对比分析了在不同变换基和测量矩阵下利用OMP 算法对回波信号的重构效果。在点回波测频模型下,基于复协方差法估计重构回波信号的频移。对比0~30 dB不同信噪比条件下,应用压缩感知方法和带通采样方法处理宽带多普勒回波信号的性能。仿真实验结果表明,应用压缩感知方法处理宽带多普勒测速的回波信号可得到比较理想的测频效果;在相同噪声条件下,应用压缩感方法处理后的回波信号能够获得与带通采样方法相当的测频效果,频移计算结果符合宽带声学多普勒测速的精度要求。压缩感知理论的应用有助于解决现有回波信号处理所需采样率高、采样数据量大和占用存储空间多的问题,可为宽带多普勒测速回波信号的数字化处理提供一种新的思路。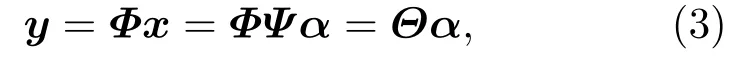
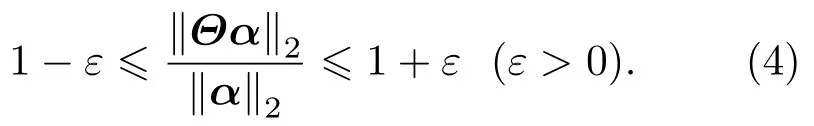
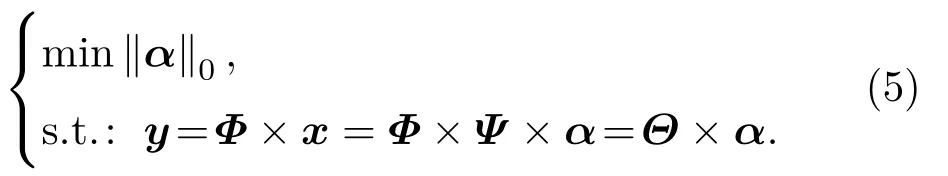
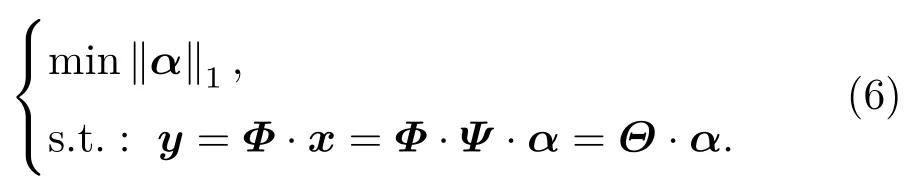
2 应用压缩感知处理宽带多普勒测速技术中的回波信号
2.1 回波信号的稀疏表达
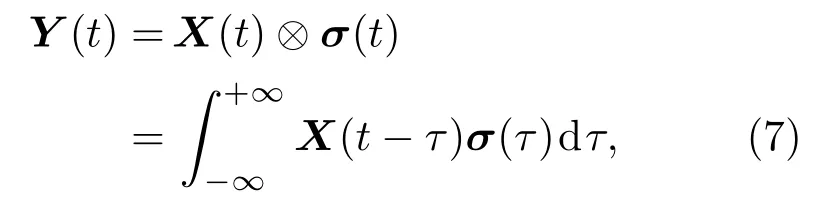



2.2 测量矩阵的选择
2.3 信号重构

2.4 适用性验证方法
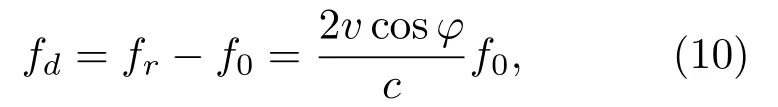

3 仿真实验及结果分析
3.1 回波信号设计
3.2 压缩感知重构回波信号仿真实验
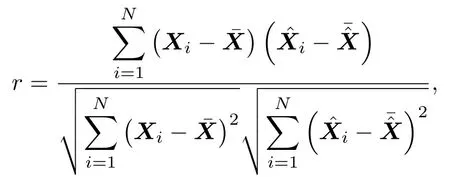

3.3 重构回波信号的频移计算


4 结论

