参数同步优化随机共振在牵引传动系统早期微弱故障诊断中的应用

尹进田， 唐 杰， 刘 丽， 刘新波， 彭志华， 李 辉

(邵阳学院 多电源地区电网运行与控制湖南省重点实验室， 湖南 邵阳 422000)

高铁的安全、质量问题，是广大人民群众非常关心的话题。快速、舒适与重载已成为高速列车的发展方向，安全是高速铁路快速发展的根本，一旦高速列车出现事故，将对生命财产造成巨大损失并产生严重的社会影响。这就要求对高速列车早期故障实行有效监测与诊断，防止故障的进一步扩大。然而早期故障的特征信号幅值和强度都很小、特征及其不明显，具有随机性和隐蔽性，易被系统扰动和噪声掩盖，要对其进行准确提取极具挑战。传统的微弱故障信号检测方法主要有自适应滤波法[1]、信号模型参数辨识法[2]、局部均值分解[3]，奇异值滤波[4]、提升多小波法[5]、独立分量分析[6]等。但是这些方法主要集中在设法抑制和消除噪声以提高信噪比。虽然这样的处理方法也表现出了较好的特性，但是在降低噪声的同时也削弱了特征信号，尤其是当噪声频率与特征信号频率接近或重合时，特征信号不可避免的受到了损害，从而极大影响了微弱信号的检测效果。

随机共振(stochastic resonance，SR) 是Benzi等[7]提出的一种利用噪声来使微弱特征信号得以增强的方法。与目前常用的通过滤波等方法滤除噪声的方法不同，它将噪声能量转移到微弱故障信号上，在降低噪声的同时使淹没在噪声中的微弱特征信号得到共振加强，从而实现强背景噪声下微弱特征信号的检测，因此近年来被用于微弱特征提取和故障诊断中。随机共振是指一个非线性双稳系统，仅在小周期信号或噪声作用下不足以使系统输出在两个稳态之间跳跃，而在噪声和小周期信号的共同作用下，系统输出频谱中，在信号的频率处出现一峰值，当噪声强度为某一适当值时输出频谱的峰值达到最大，这就是SR现象。由于受到绝热近似理论、本征值理论的限制[8]，传统的随机共振只适合信号的幅值、频率以及噪声强度都很小的小参数信号[9]。

高速列车系统发生故障时故障特征信号频率范围通常在几十到上千赫兹甚至更高，特征信号幅值和噪声强度也都远远超出传统随机共振的适用范围，此时经典随机共振理论无法使用，因此要实现对这类大参数信号的检测，需要采取措施将其变换成小参数信号。文献[10-11]采用移频和变尺度双重变换将大参数信号变换为小参数信号，从而实现了对大参数信号的检测；文献[12]采用二次采样随机共振解决上述问题；文献[13]采用调制随机共振实现随机共振理论在工程信号检测中的应用。传统的及当前已出现的随机共振方法基本为固定随机共振参数或只对单一参数进行优化[14-15]，并未考虑参数间的相互作用，影响了随机共振对微弱故障特征的提取。

本文提出一种基于状态转移算法的参数同步优化随机共振新方法用于诊断牵引传动系统早期微弱故障，该方法采用移频变尺度方法将大参数信号变换成小参数信号，通过状态转移算法对随机共振系统的参数进行同步优化，以最大信噪比为优化目标，可同时获取系统最优参数，从而有效削弱信号中的噪声和增强微弱特征，实现早期故障准确诊断，该方法检测误差低、精度高。通过对牵引电机早期故障诊断仿真和试验，验证了该方法的有效性和实用性。

1 背景原理

1.1 双稳系统随机共振

随机共振是指一定的非线性条件下，弱周期信号与噪声达成协同作用而使输出信号的信噪比增强的现象。随机共振模型一般包括3个基本要素：微弱的输入信号、噪声以及非线性系统。随机共振的经典模型有很多，其中应用最广泛的是双稳态系统，双稳态系统可以用Langevin方程来表示[16]

(1)

图1 双稳系统随机共振模型Fig.1 SR model of a bistable system

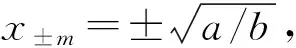
a=b=1时，SR仅适用于极低频的信号，一般要求周期驱动信号频率ω<<1，可通过变换拓展SR的适用频率。对于高频信号，可以通过选取适当的参数a将高频信号转化为低频信号来进行处理，通过选取适当的参数b可以适应强弱不同的输入信号。

图2 双稳势函数曲线图Fig.2 Bistable potential function curve

信噪比是定量描述经典随机共振最常用的测度指标，信噪比表达式为

(2)

式中:S(ω)为输入信号功率谱密度；ω代表信号频率；SN(ω)为输入信号频率周围噪声强度大小。

1.2 状态转移算法

状态转移算法(state transition algorithm, STA) 为基于状态空间转移思想的新型有效随机搜索算法，该算法是把优化问题的解作为状态，将在搜索空间进行搜索的过程视为状态转移过程的一种进化算法[17]。该算法由Zhou等提出，将旋转 (Rotation operator)、扩展(Expansion operator)、转移(Translation operator)和平移(Axesion operator)四种操作算子用于连续优化问题的求解，该算法全局搜索能力强、搜索精度高以及收敛速度快[18]。

STA可以表示为

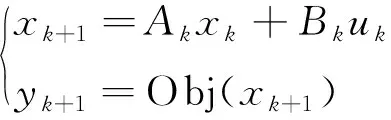
(3)

式中:xk和xk+1分别表示当前状态和转移后的状态，对应于优化问题的解；Ak和Bk为状态转移矩阵；uk为xk和历史状态的函数；Obj表示目标函数。

为求解连续优化问题，引入四个变换因子：

(1) 旋转算子

(4)

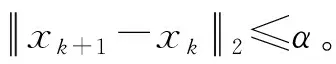
(2) 转移算子

(5)

其中，β是一个正数，称为转移因子。Rt∈R是[0,1]之间服从均匀分布的随机数。该算子使算法沿着xk到xk+1梯度正方向进行搜索，搜索步长最大为β。

(3) 扩展算子

xk+1=xk+γRexk

(6)

其中，γ是一个正数，称为扩展因子。Re∈Rn×n是一个随机诊断矩阵，矩阵中元素服从高斯分布。扩展算子能够在整个搜索空间进行全局搜索。

(4) 平移算子

xk+1=xk+δRaxk

(7)

其中，δ是一个正数，称为平移因子。Ra∈Rn×n是一个随机诊断矩阵，矩阵中元素服从高斯分布，且矩阵中只有一个随机位置上的元素不为零。

状态转移算法基本流程如图3所示。

图3中的SE为种群个体数，best为最优个体，α、β、γ、δ为四个因子，转移操作嵌入到扩展、旋转和平移3步操作中进行。

图3 状态转移算法流程图Fig.3 Flowchart of STA

2 状态转移自适应随机共振

根据绝热近似理论，随机共振理论成立的前提是要求输入信号的幅值大小、频率大小和噪声强度必须处在小参数范围内，即三者远远小于1。因此，在将信号输入双稳态随机共振之前，需要对输入信号进行调制、归一化、移频变尺度等方法处理，使之满足小参数的要求，本文使用移频变尺度方法实现信号预处理，即

对实测信号的频率进行线性压缩，然后按Langevin方程分析系统响应SR谱，得到微弱信号的频谱特征，最后按照设定的压缩尺度比还原实际测量数据。

为克服传统移频变尺度随机共振只对单一参数进行优化，忽略系统各参数间交互作用的缺陷，本文提出的基于状态转移自适应移频变尺度随机共振可实现对系统参数a、b的同步优化，其中状态转移算法以最大信噪比作为优化目标。

状态转移自适应随机共振方法流程图如图4所示，其分为以下几个步骤：(1) 数据采集，并对数据进行高通滤波；(2) 采用移频变尺度对采集数据进行处理，使之满足输入信号小参数要求；(3) 对状态转移算法的变量进行初始化，并建立信噪比最大目标函数；(4) 采用状态转移算法同步优化参数a和b；(5) 将最优a和b作为随机共振参数；(6) 通过随机共振检测到微弱故障特征；(7) 恢复微弱故障特征的频率和幅值；

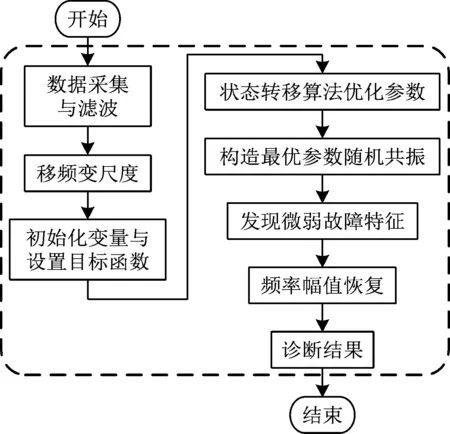
图4 状态转移自适应随机共振流程图Fig.4 Flowchart for STA-based adaptive SR

(8) 根据故障特征频率诊断所发生故障。

其中，移频变尺度具体流程如下：

(1) 让输入信号通过高通滤波器消除低频干扰；

(2) 将滤波后的输出信号与高频载波信号相乘，实质为信号的频谱沿频率轴线性频移，实现信号频谱向低频的一次搬移；

(3) 设置压缩比，得到符合随机共振要求的小参数信号。此时信号频率为

fout=(fin-fc)/R

(8)

式中：fout表示小参数信号频率；R表示压缩比；fin表示采集信号频率；fc表示高频载波信号频率。

3 案例研究

3.1 仿真案例

为验证方法的有效性，设输入信号为s(t)=0.01×cos(2×π×0.005×t)，在该信号中加入均值为0、强度为0.02的高斯白噪声，采样点数为8 000，采样频率为5 Hz。图5为输入信号原始时域波形及频谱分析，可看出图5(b)频谱中无法找出输入周期信号的频率。

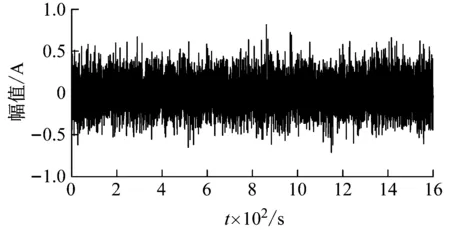
(a) 时域波形

(b) 频谱图5 输入信号时频域波形Fig.5 Input signal shown in time and frequency domains

将原始信号输入到经典随机共振系统中，其参数设置方法是a、b随机输入，或固定其中一个参数，在一定范围内寻优另外一个参数，以信噪比作为评价随机共振优劣的标准。图6为固定参数a=0.1，在范围[0，5]内取值参数b，结果显示当b=0.9440时, SNR=33.7 dB最大。

图7为固定参数b=1，在范围[0，5]内取值参数a，结果显示当a=0.067 0时，SNR=29.3 dB最大。

(a) 信噪比曲线

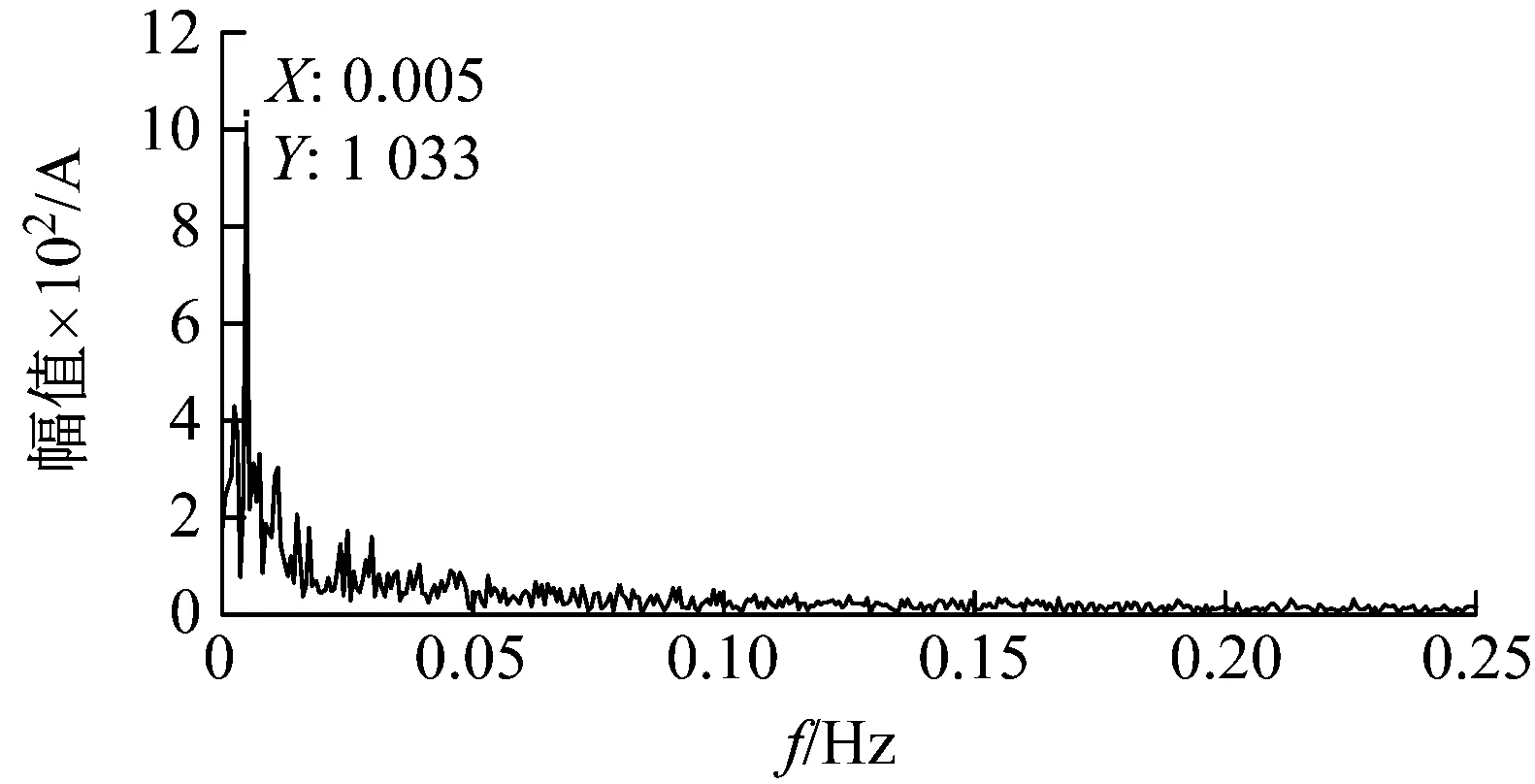
(b) 信噪比最大时的输出信号频谱图6 固定a取值b的随机共振分析结果Fig.6 SR analysis results: fixed a, variable b

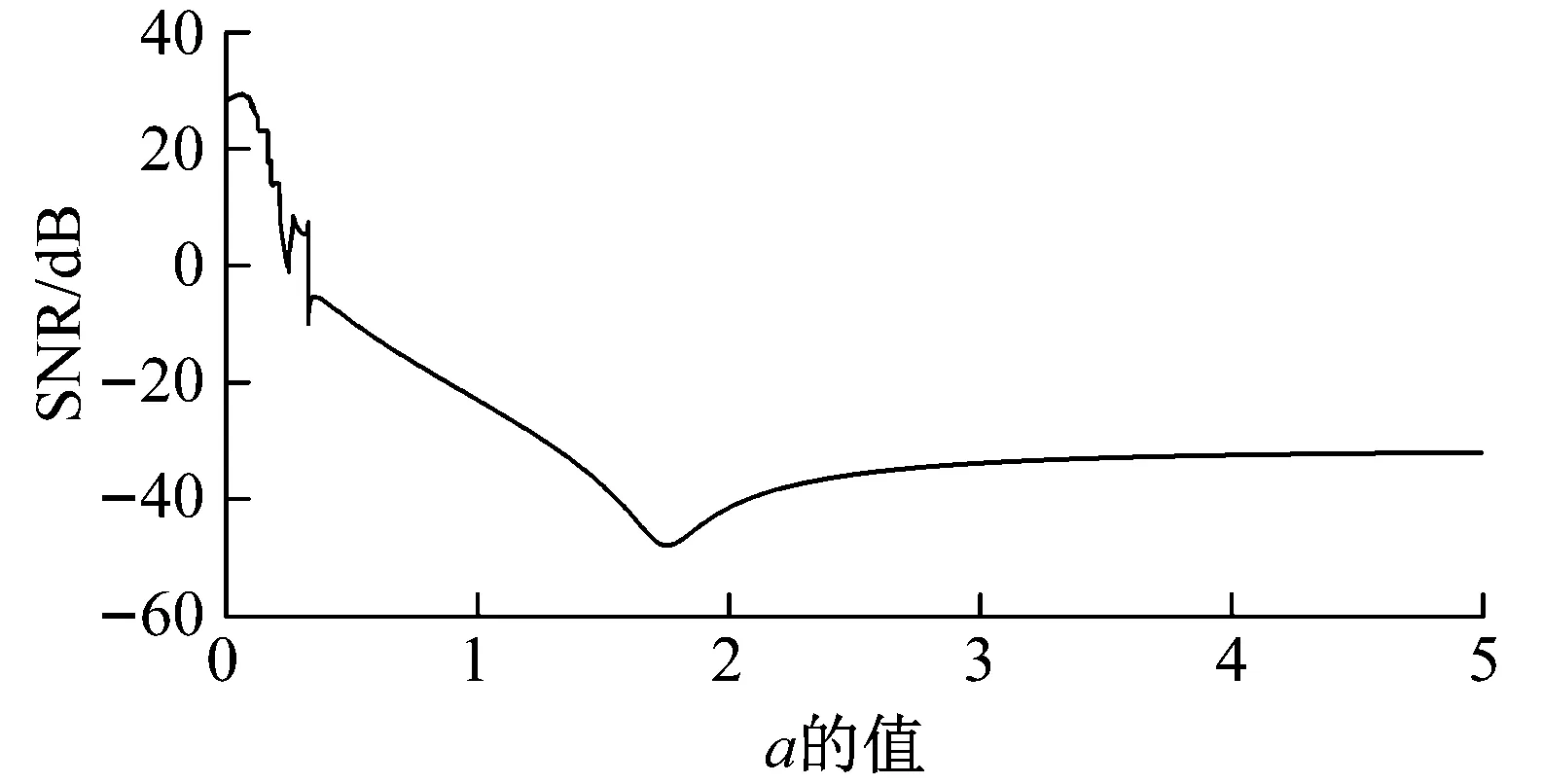
(a) 信噪比曲线

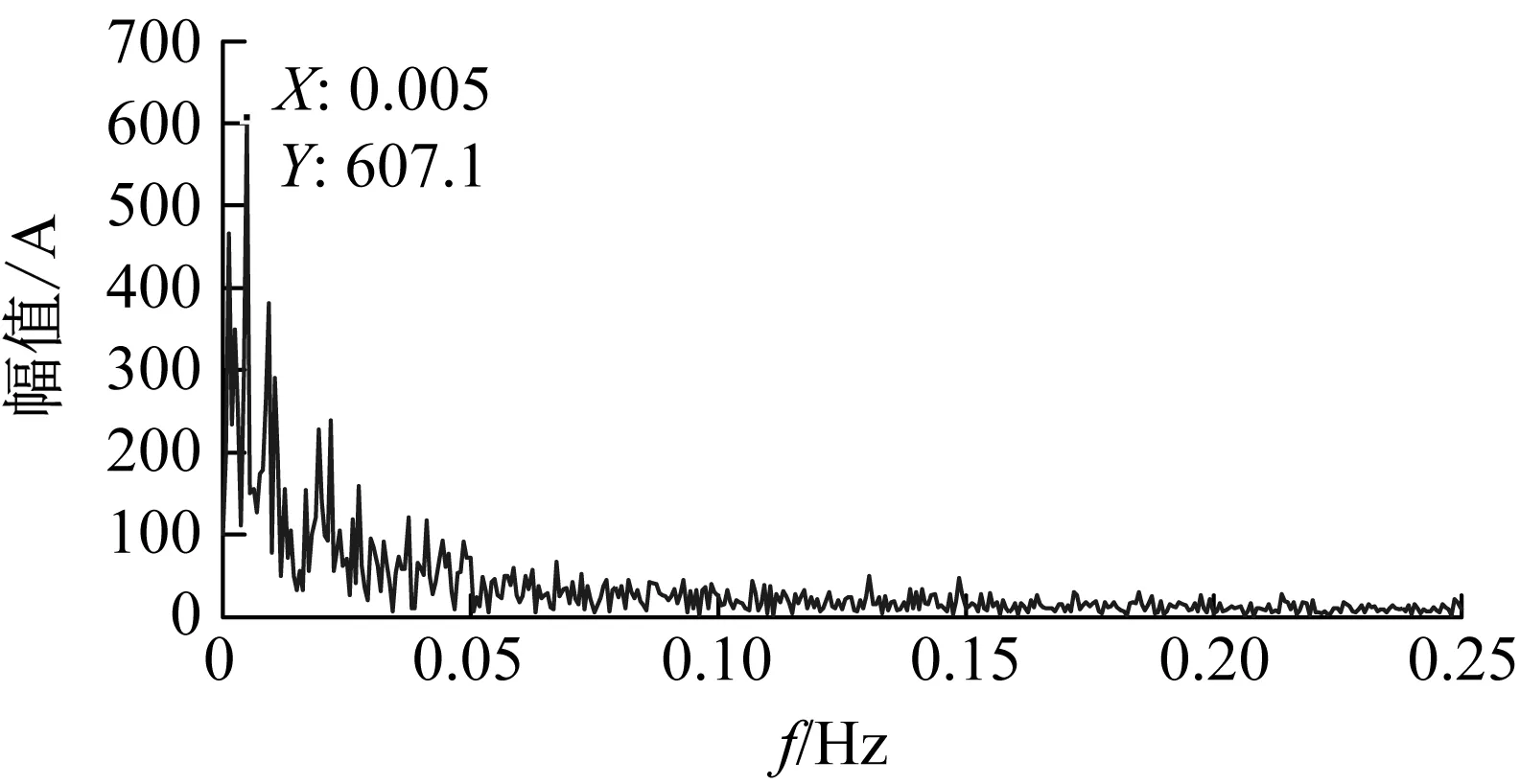
(b) 信噪比最大时的输出信号频谱图7 固定b取值a的随机共振分析结果Fig.7 SR analysis results: fixed b, variable a

采用状态转移随机共振方法来处理分析上述仿真信号，通过状态转移算法在[0，5]范围内同步寻优系统最佳参数。寻优结果a=0.229 8，b=4.143 6，此时输出信噪比SNR=39.8 dB，比传统分别固定a和b的方法分别提高了18.1%和35.8%，自适应随机共振处理后的时域信号及频谱如图8所示。比较图8与图6、图7发现，所提方法的随机共振输出效果更好，非常适合检测微弱故障。

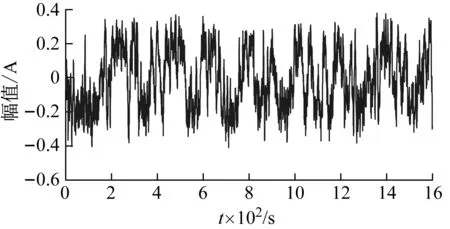
(a) 时域波形

(b) 频谱图8 状态转移随机共振分析结果Fig.8 Results of STA-based adaptive SR analysis

3.2 硬件在环故障注入平台案例

牵引电机常见故障有轴承故障、转子断条故障、定子绕组匝间短路故障、气隙偏心故障等，其中转子断条是牵引异步电机常见故障之一，约占电机总故障的8%。早期转子断条故障是指电机从正常到一根导条完全断裂的状态，在转子断条故障发生早期将其检测出来，对于避免严重故障发生实现机组的健康运行具有重要现实意义。

试验装置采用基于dSPACE的CRH2动车组牵引传动控制系统控制器在环实时故障半实物平台，如图9所示，包括实时仿真器、故障注入单元FIU、实物牵引传动控制单元TCU、实时数据采集与监控单元等。其中控制器为实物；dSPACE硬件包括DS1007CPU板、DS5203FPGA板、DS4004数字I/O板、DS2103多通道高精度的D/A板，用于搭建牵引异步电机及主电路并实现通讯。故障注入Benchmark由牵引变流器、牵引电机、传感器、牵引传动控制器TCU四个故障注入模块组成，采用信号调理的方式构建，文献[19-20]作了较详细的介绍，故障注入仿真平台可通过网站下载。故障注入单元实现了对牵引传动控制系统中牵引电机转子断条早期微弱故障注入，根据牵引电机转子断条故障的特点生成特定的故障信号，与故障注入点处的注入前正常信号进行信号调理，生成故障注入后的信号，即故障注入信号；再将该信号替换正常信号注入到故障注入点，从而实现牵引电机转子断条故障注入。

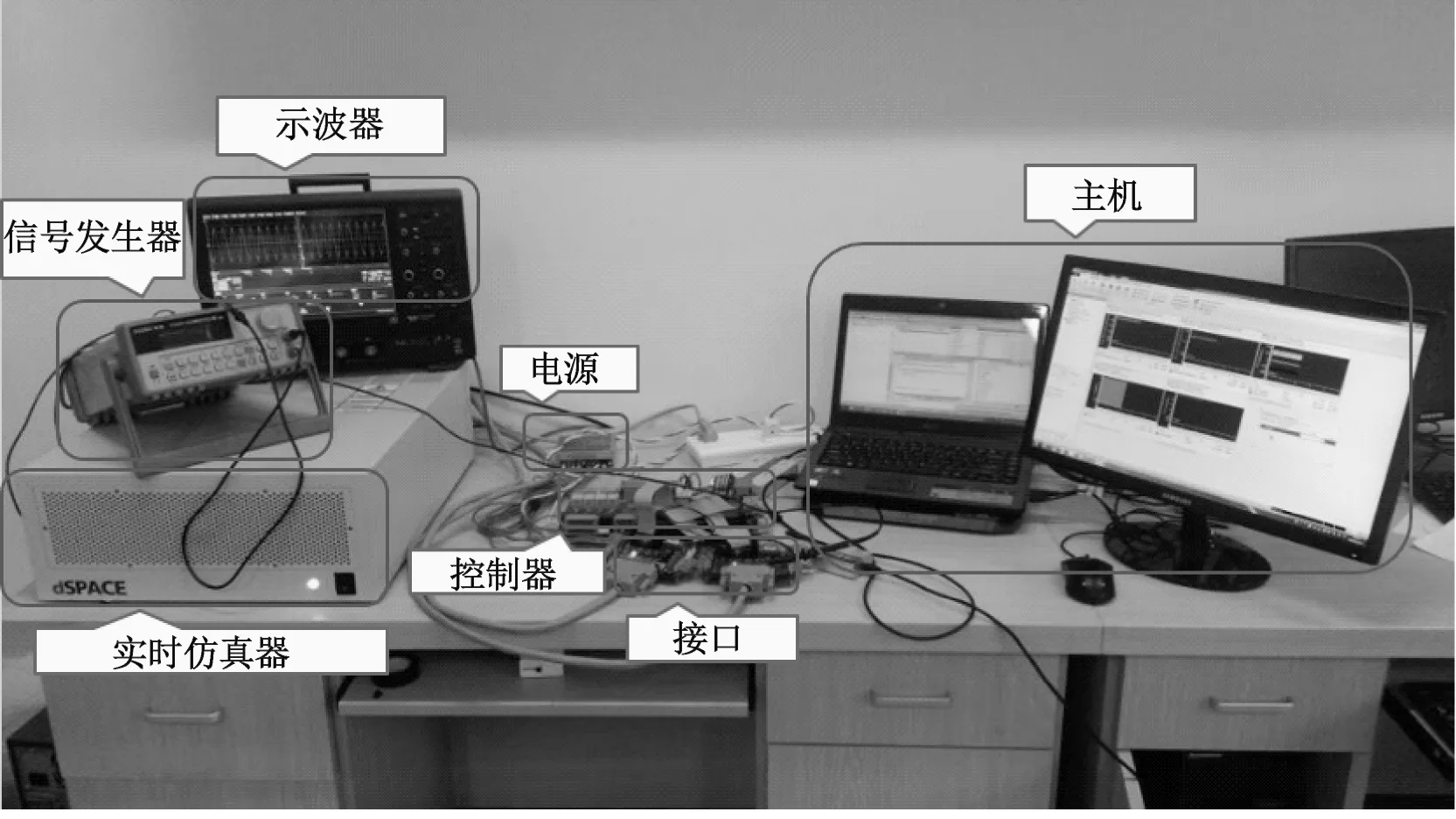
图9 CRH2型动车组牵引传动系统半实物平台Fig.9 Semi-physical platform of the CRH2 EMU traction drive system

CRH2动车组牵引传动控制系统主要参数如表1所示，平台稳定运行后的电机转速为3 860 r/min，列车时速为200 km/h；牵引电机负载转矩大小与列车运行速度及列车本身参数有关，稳定运行时为210.7 N·m；转子断条故障发生时，电机定子电流中会产生A2cos(2π(1-2s)ft+θ2)、A3cos(2π(1+2s)ft+θ3)的谐波电流，即转子断条故障特征频率计算公式：fD=(1±2s)f[21-22]，式中：fD为牵引电机转子断条故障特征频率；s为电机转差率，s=0.018；f为加载到电机定子三相绕组上的电压频率，f=131 Hz。计算得fD1=135.7 Hz和fD2=126.3 Hz，因为这两个频率总是成对出现的，因此检测到其中一个故障频率如fD1=135.7 Hz即可判定发生断条故障。

表1 系统仿真平台的电气参数Tab.1 Electrical parameters of the system simulation platform

考虑现场背景噪声的影响，在试验测得的电机定子电流信号基础上，添加高斯白噪声。由于理论故障特征频率为135.7 Hz，因此高通滤波器的通过频率设为135 Hz，载波频率与高通滤波器的通过频率一致，为135 Hz，采样频率100 000 Hz，频率压缩比为1 000。图10给出了转子断条早期微弱故障情况下定子A相电流原始信号的波形及频谱。由图可见时域信号中背景噪声强烈，淹没了转子断条故障的特征成分。频谱中，局部放大了135～200 Hz区域，在故障特征频率处也不能检测到明显的谱峰。考虑到实际牵引传动系统背景噪声更强烈，因此，时域信号和频谱中的背景噪声将完全掩盖转子断条故障特征，使得无法判断转子导条是否存在故障，造成漏诊或误诊。

采用传统移频变尺度随机共振对信号进行分析。图11(a)为固定参数a=1，自动寻优b的值，b的寻优范围为[0,10]，使得系统输出信噪比最大，通过寻优b=0.03，此时SNR=40.4 dB；图11 (b)为固定参数b=1，自动寻优a的值，a的寻优范围为[0,10]，使得系统输出信噪比最大，通过寻优a=4.52，此时SNR=45.2 dB。

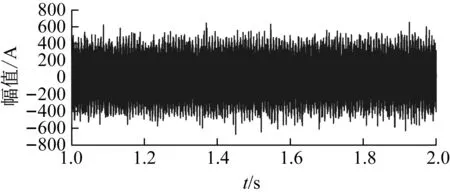
(a) 时域波形

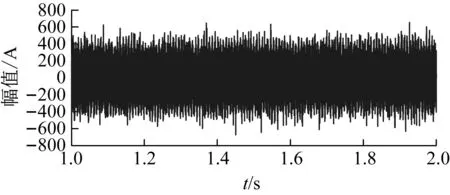
(b) 频谱图10 加入噪声的断条故障实际信号Fig.10 Actual signal of the broken rotor bar fault with added noise

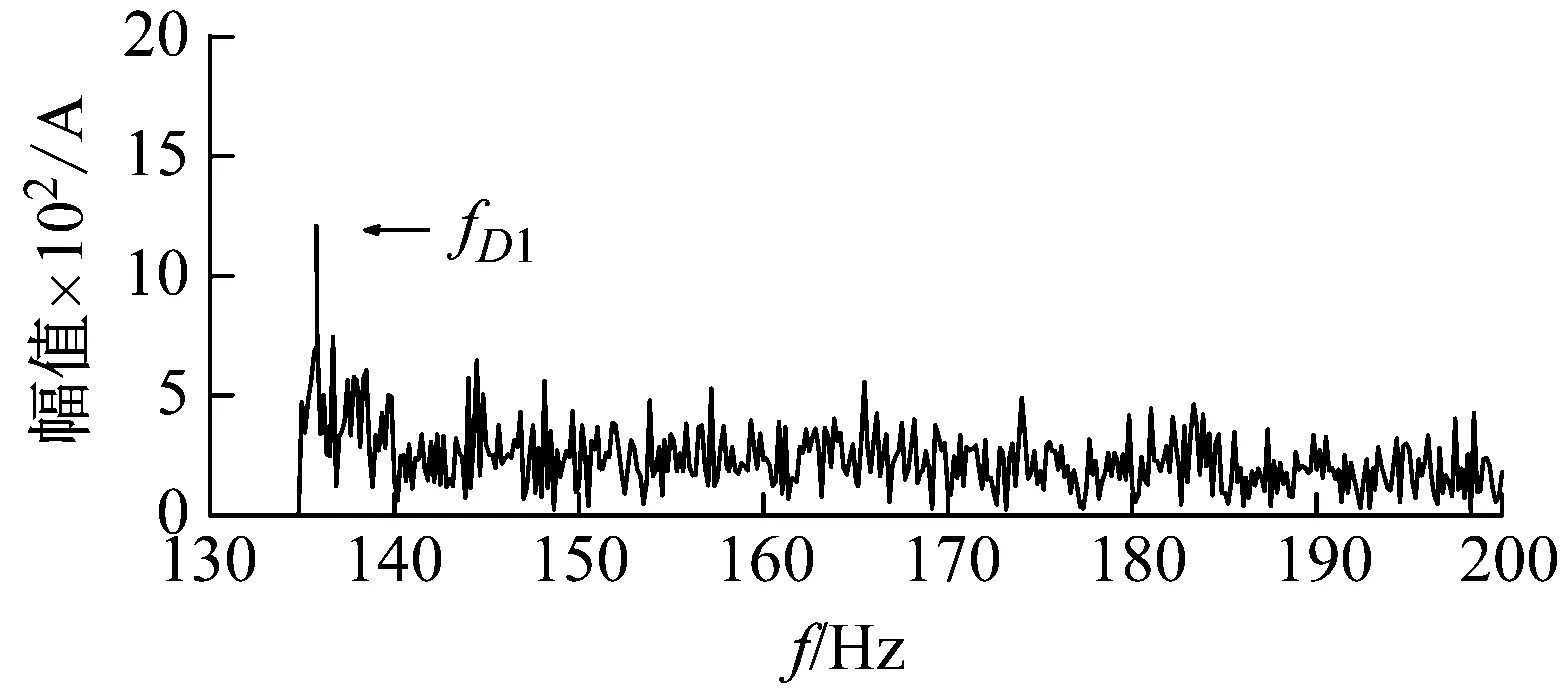
(a) 固定a优化b

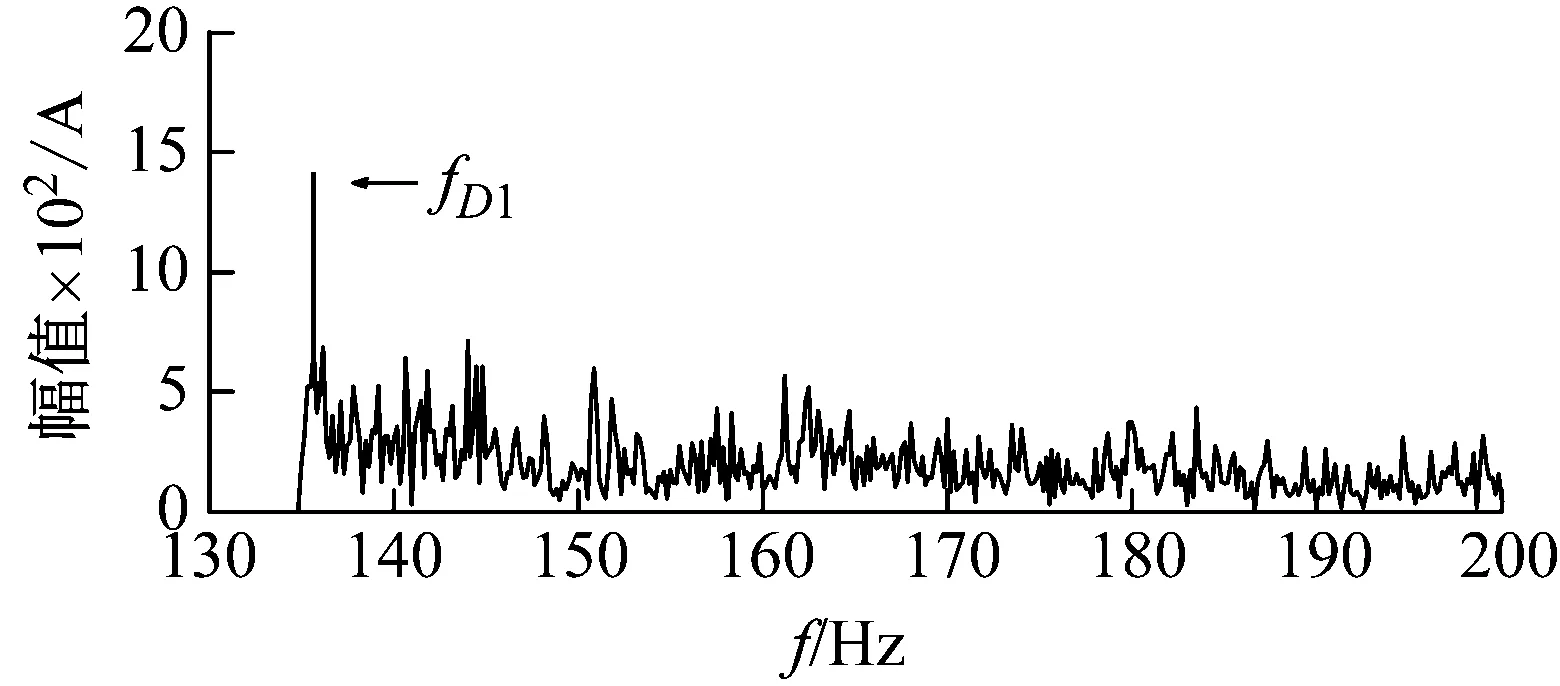
(b) 固定b优化a图11 传统随机共振分析结果Fig.11 Actual signal of the broken rotor bar fault with added noise

利用状态转移自适应随机共振对信号进行分析，设搜索力度为20，问题维数为2，两个待优化参数的范围为[0,30]，迭代次数为30，经过该随机共振后的输出波形如图12所示，此时a=1.575 4，b=21.230 3， SNR=51.7 dB。

对比图11(a)、11(b)与12(b)，发现状态转移算法具有更高的谱峰值，SNR值分别增加了28.0% 和14.4%。

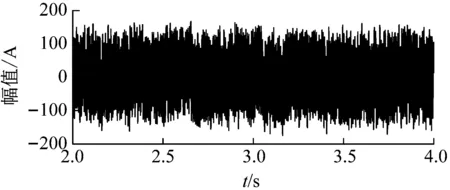
(a) 自适应随机共振输出时域波形

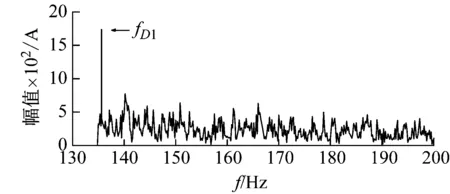
(b) 自适应随机共振输出频谱图12 状态转移自适应随机共振输出结果Fig.12 Results of STA adaptive SR analysis

3.3 与已有存在的方法比较

进一步阐明所提出的基于状态转移自适应随机共振方法对于微弱故障的诊断性能，在SNR输出结果、实测故障特征频率与理论公式计算故障特征频率(135.7 Hz)比较两方面同几种存在的方法，如遗传自适应随机共振、粒子群自适应随机共振以及差分自适应随机共振、SVD，小波等诊断效果进行对比，SNR输出结果及实测频率如表2所示。从中可以看出，对相同输入信号进行分析，状态转移自适应随机共振输出结果具有更高SNR，且实测故障特征频率与理论故障特征频率一致。说明状态转移自适应随机共振更适合类似牵引电机转子断条微弱特征信号的提取。

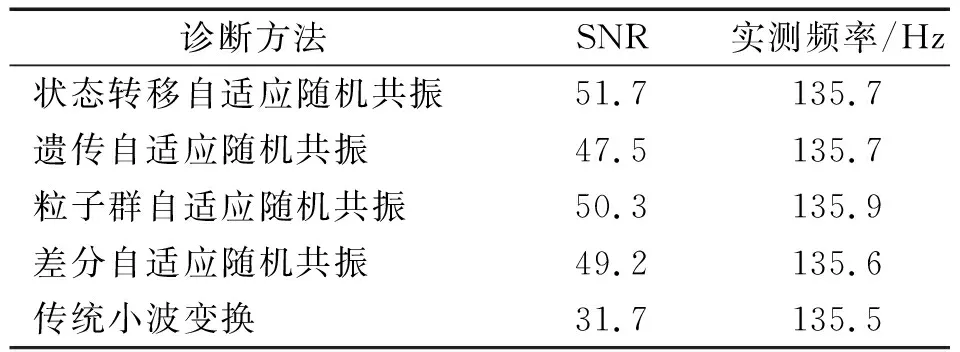
表2 几种存在的微弱故障诊断方法比较Tab.2 Comparisons between the proposed method and exiting methods

工程试验结果表明，对于牵引异步电机早期转子断条故障信号，传统随机共振方法的处理结果较原始频谱有一定改善。而本文提出的自适应随机共振方法充分利用状态转移算法的全局搜索特性，能考虑系统参数之间的交互作用，同时优化系统参数，因此提出的自适应随机共振方法在牵引异步电机转子断条早期故障诊断中获得了更好结果，并且该方法相比遗传自适应随机共振、粒子群自适应随机共振、差分自适应随机共振及传统小波变换更具优势。

4 结 论

本文提出一种状态转移参数同步优化随机共振方法用于解决高速列车系统早期微弱信号故障诊断。针对实际系统早期故障特征微弱且淹没在强噪声背景下的特点，首先利用移频变尺度对大参数信号进行预处理；其次利用状态转移算法全局搜索能力，以最大信噪比为优化目标，自适应选择和同步优化随机共振参数；最终实现微弱故障特征信号的最优提取。该方法在高速列车牵引传动控制系统硬件在环故障注入半实物平台上以牵引异步电机转子断条微弱故障为例进行了验证，试验结果表明所提方法与传统随机共振及其他已存在方法相比具有较明显的优势，验证了其在早期微弱故障诊断中的有效性。