钢弹簧隔振减震装置性能试验及其结构振动控制参数分析

付伟庆， 赵 鹏， 韩艳艳， 高云锋， 王 建

(1. 青岛理工大学 土木工程学院， 山东 青岛 266033；2. 蓝色经济区工程建设与安全协同创新中心(青岛理工大学)， 山东 青岛 266033；3. 隔而固(青岛)结构设计事务所有限公司， 山东 青岛 266108)

随着城市扩张和人群聚集，地下轨道网络密布，城市交通建设蓬勃发展，城市交通工具的运行势必会造成沿线建筑物的环境扰动[1-4]，因此城市交通干道附近的建筑结构不仅应满足抗震设计要求，还需满足环境振动控制要求。传统隔震结构较多使用橡胶支座、摩擦摆和黏滞阻尼器等装置，此类装置对竖向轨道交通和公路交通引起的高频竖向振动减振效果均不明显[5-7]。为了应对这种情况，钢弹簧隔振器已被广泛应用于地铁等城市交通轨道浮置板中，用以隔离地铁竖向扰动对周围环境的影响，其具有竖向抗压能力强，反应灵敏，性能参数稳定等特点[8-10]。近年来，由钢弹簧隔振器和阻尼筒组成的钢弹簧隔振减震装置(图1)被应用于地铁附近建筑结构设计中，其可对竖向环境振动和水平向地震动引起的结构振动进行控制，该装置已在北京远洋万和公馆别墅、青岛新机场、上海音乐厅等建筑的建设中得到应用[11-13]。

图1 钢弹簧隔振减震装置Fig.1 Steel spring vibration isolation device

由于被控对象体量和受城市交通扰动程度不同，隔振减震结构设计时各安装点的装置中的钢弹簧数量和阻尼筒的阻尼系数明显不同。在对钢弹簧隔振减震装置的实际工程应用中，由于未进行钢弹簧隔振减震装置对结构振动控制效果影响的系统参数分析，并缺乏对钢弹簧隔振减震装置的试验研究，设计过程中大多采用验算法满足设计要求，装置的性能参数取值为理论值，设计过程在安全性和实用性上存在不足，这些问题严重制约了该装置的工程推广应用[14-15]。另外，装置振动控制性能如果不足，将对建筑结构使用舒适性和抗震安全性产生不利影响。

本文首先通过压剪性能试验和阻尼耗能试验，对钢弹簧隔振减震装置中的钢弹簧和阻尼套筒分别进行了竖向和水平向试验检测和相关性能参数确定。接着针对采用钢弹簧隔振减震装置的Benchmark模型结构，进行了竖向环境激励输入和水平向罕遇地震波输入下的动力反应数值计算，分析不同装置参数对结构振动控制效果的系统影响，研究确定装置中隔振器和阻尼器有效参数的取值范围。研究成果可为钢弹簧隔振减震装置在结构振动控制设计应用提供参考和指导。

1 钢弹簧隔振减震装置性能试验

由于装置中的钢弹簧隔振器和阻尼筒分别属于位移相关型和速度相关型，二者有效工作条件存在差异。因此，对两构件分别进行装置性能试验，及双向性能参数分析。

1.1 隔振器压剪性能试验

通过压剪性能试验，获得钢弹簧隔振器竖向和水平向刚度参数值。

1.1.1 试验试件组成

为研究钢弹簧隔振器在压力作用下的水平向变形能力并确定钢弹簧隔振器的力学性能参数，对钢弹簧隔振器进行压剪性能试验，试验对象是由4个钢弹簧和上、下钢盖板组成的钢弹簧隔振器，如图2所示，其具体尺寸和力学性能理论值如表1所示。试验使用的四个钢弹簧隔振器，分别命名为1#、2#、3#、4#。

图2 钢弹簧隔振器试件Fig.2 SSVI

表1 钢弹簧隔振器试件参数Tab.1 Construction parameters of steel spring vibration isolator

1.1.2 试验装置工况

压剪性能试验由一台200 kN电液伺服作动器进行竖向加载，一台100 kN电液伺服作动器进行水平向加载，试验加载装置如图3所示。

图3 试验加载装置Fig.3 Test setup

为了确定钢弹簧隔振器在不同竖向荷载下的水平刚度，本次研究设定了十组试验工况，详细工况设定如表2所示，试验中选择位移控制的加载方式使隔振器下盖板水平往复位移。工况1～工况7为水平向剪切性能试验，位移限值固定，测试隔振器正常工作下的力学性能；工况8～工况10水平向压剪极限试验，加载至钢弹簧隔振器进入屈服阶段，测试隔振器的水平向剪切变形能力。

1.1.3 试验结果分析

试验对隔振器的竖向和水平向力学性能进行分析，重点对水平向屈服性态进行研究。

(1) 竖向弹性阶段

为获得钢弹簧隔振器的竖向刚度，对1#试件按2 mm/s速度施加竖向压力，测得竖向力和位移曲线如图4所示。竖向力与变形呈线性关系，经计算钢弹簧隔振器的竖向刚度实测值为4.018 kN/mm。

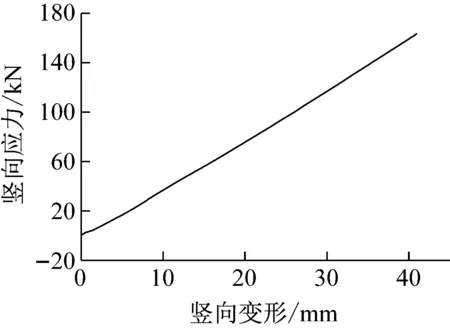
图4 竖向力-变形曲线Fig.4 Vertical pressure-deformation curve

(2) 水平向弹性阶段

为获取不同竖向压缩状态下钢弹簧隔振器的水平刚度，做出试验中第三次循环加载前40 mm形变的水平变形和剪切力曲线,如图5所示，然后进行线性拟合，计算三个隔振器在不同竖向压缩状态下的平均水平向刚度，不同压缩状态下，钢弹簧隔振器的水平刚度参数如表3所示。

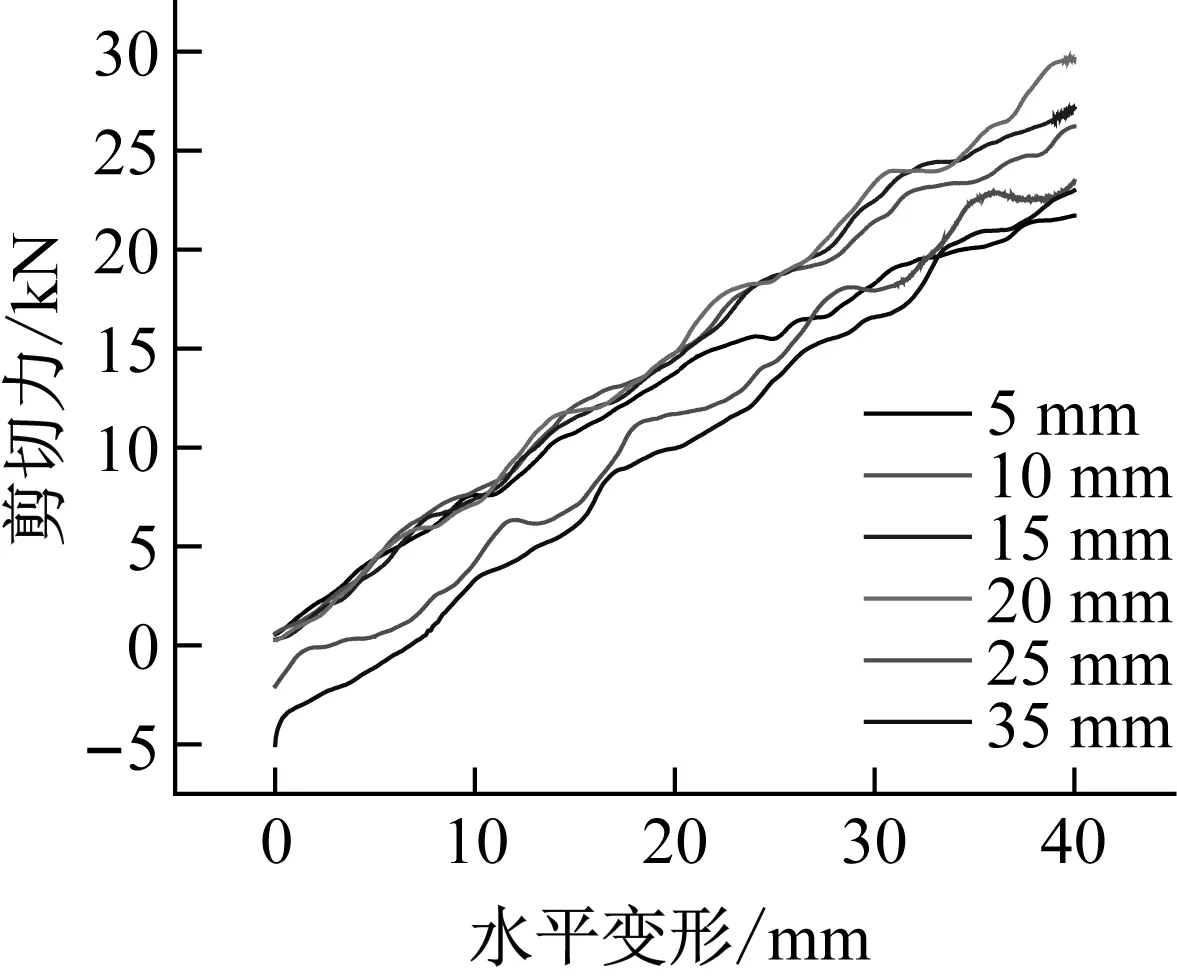
图5 剪切力-水平变形曲线Fig.5 Vertical pressure-horizontal stiffness curve

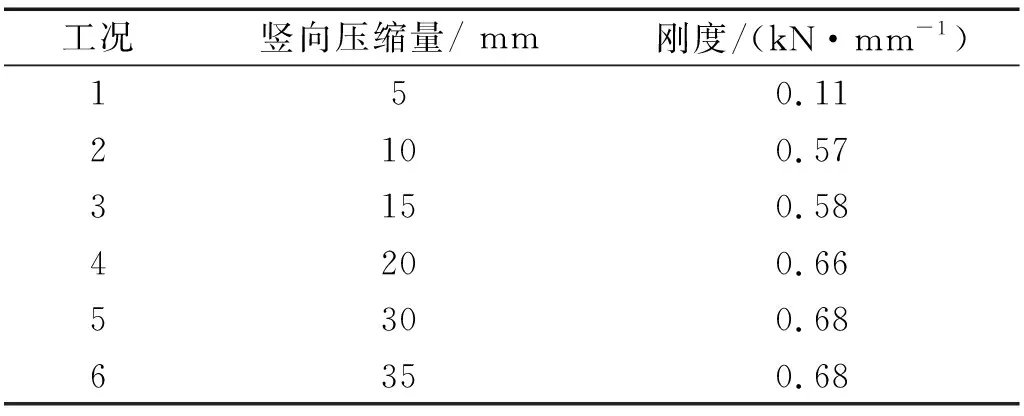
表3 钢弹簧隔振器的水平刚度参数Tab.3 Horizontal stiffness parameters of SSVI

(3) 水平向屈服破坏阶段

为研究钢弹簧隔振器的极限压剪性能，试验进行了压剪极限试验，测得四个试件力和位移的滞回曲线如图6所示，从图中看出，钢弹簧隔振器的水平向形变稳定限值为93.9 mm，屈服力为62.21 kN；试验中，当钢弹簧隔振器形变量的达到稳定限值后，试件中钢弹簧的边界条件改变，剪切力骤降，钢弹簧隔振器失稳，水平刚度迅速减小，屈服后的水平向变形很小即呈现脆性破坏，说明装置中的钢弹簧隔震器水平向不具备耗能能力。

1.2 阻尼器耗能性能试验

通过对阻尼筒两个方向频率、幅值控制下的循环加载试验，获得阻尼器双向滞回耗能曲线和阻尼系数参数值。

1.2.1试验试件

为研究阻尼筒在循环荷载作用下的耗能能力并确定阻尼筒的力学性能参数，对阻尼筒进行循环加载耗能试验，本次试验对象是由上盖板、桶装CRDS阻尼液和阻尼杆组成的油式阻尼筒，如图7所示，在荷载作用下，阻尼杆搅动黏滞阻力较大的阻尼液波动，波动过程中产生阻尼力，从而进行耗能。试件具体尺寸如表4所示。

图7 阻尼筒Fig.7 Damping tube

表4 试件尺寸参数Tab.4 Device parameters

1.2.2 试验装置及工况

由一台300 kN电液伺服作动器进行竖向阻尼试验，一台100 kN电液伺服作动器进行水平向阻尼试验，试验加载装置如图8所示。为了研究加载频率和加载幅值对阻尼筒性能的影响，设定不同加载幅值和加载频率的竖向阻尼试验工况以及水平向阻尼试验工况，详细试验工况如表5和表6所示。

表5 竖向阻尼试验工况Tab.5 Vertical damping test conditions

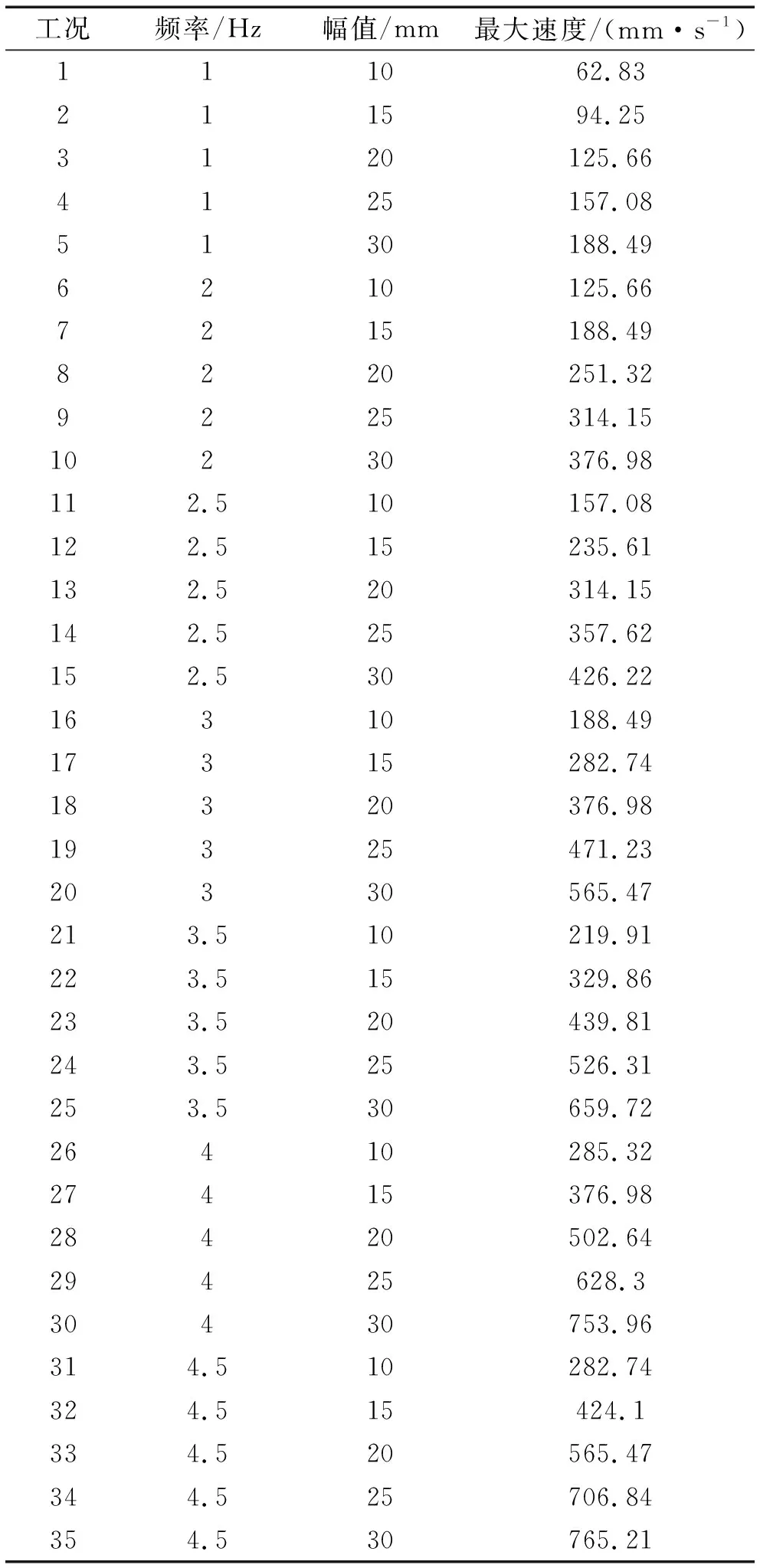
表6 水平向阻尼试验工况Tab.6 Horizontal damping test conditions

1.2.3 试验结果分析

(1) 滞回曲线分析

由于篇幅有限，以下绘制了竖向阻尼试验工况1的位移和力加载滞回曲线(图9)，以及阻尼力和加载位移的滞回曲线(图10)，从图中看出，竖向和水平向的位移和力滞回曲线饱满，阻尼筒表现出良好的耗能能力。从速度与力的滞回曲线形状看出，在数值模拟计算中可将阻尼筒定义为线性阻尼单元。

(2)参数分析

(1)

为分析加载频率和加载幅值对阻尼筒性能的影响，选取循环加载第三周期的试验数据，根据式(1)计算各工况下阻尼筒的阻尼系数。式中S是第三次加载循环力与位移滞回曲线的面积，C是阻尼筒的阻尼系

数，L是试验加载幅值，f是试验加载频率。

图11表现出阻尼筒的竖向阻尼系数与加载频率、加载幅值的关系，图11(a)表示当加载频率大于等于3 Hz时，阻尼筒的阻尼系数随着加载频率的增大而减小；图11(b)表示当试验加载幅值大于等于5 mm时，阻尼系数随着加载幅值的增大而减小。分析其原因，试验中阻尼杆通过与阻尼液的黏连带动阻尼液波动产生阻尼力，从而进行耗能。当加载频率增加到3 Hz以后，或加载幅值增加至5 mm以后，随着加载幅值和加载频率的增加，阻尼杆和阻尼液的黏连作用减弱，耗能能力降低，阻尼系数降低，滞回曲线面积减小。

图12为各工况试验试件的水平阻尼系数与频率、幅值的关系，从图中看出，当加载频率大于1 Hz或加载幅值大于等于10 mm，阻尼筒的阻尼系数随着加载频率和加载幅值的增大而减小。分析其原因，随着加载幅度和加载频率的增加，阻尼杆和阻尼液的黏连作用减弱，阻尼液波动减弱，阻尼系数降低。

2 Benchmark隔震结构模型与输入激励介绍

2.1 Benchmark计算模型

Benchmark模型(Spencer等)[16]，作为一个标准化计算模型，如图13所示，可以对不同控制方式的结构减震效果进行试验和数值计算。该计算模型结构总共20层，东西方向6跨，南北方向5跨，跨间距均为6.1 m。该结构地上20层，除首层5.5 m外，其它层均为4 m。

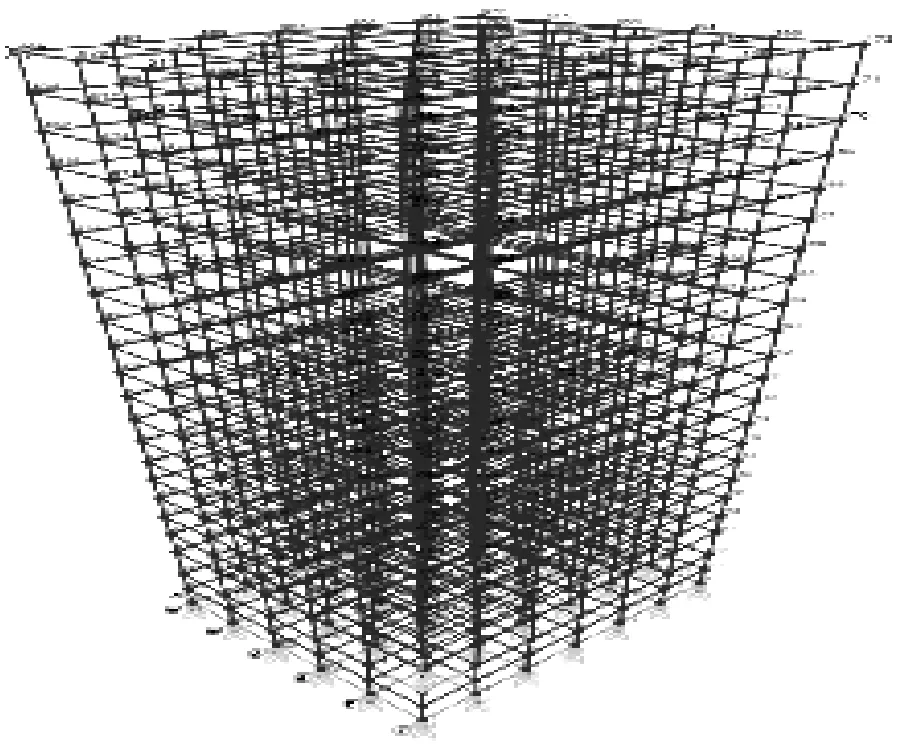
图13 结构模型Fig.13 Structure model

2.2 竖向环境激励输入

模型结构动力反应计算所使用的环境激励，是在北京某地块采集的振动信号C7、C8、C10、OZ1，北京地铁6号线隧道穿过该地块的西南角，地铁8号线及延长线位于地块北侧，振动信号时程曲线如图14所示。

将采集到的振动信号时程曲线转换成频谱曲线如图15所示，从图中看到，C10和OZ1测点信号主频在50～80 Hz，主要为地铁信号；C7和C8测点信号主频在10～20 Hz和50～80 Hz，为地铁和路面交通激励叠加信号。

2.3 水平向地震动输入

隔震体系水平抗震参数分析时，输入地震波选用8度和9度的El Centro波、Taft波、以及一条人工合成波，人工合成波水平向和竖向时程曲线如图16所示，地震动输入情况如表7所示。

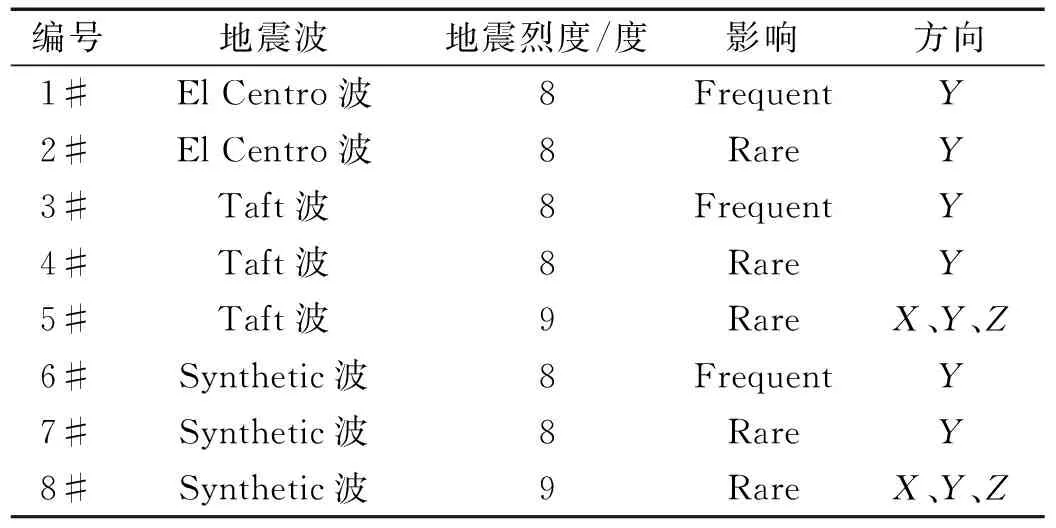
表7 地震输入工况Tab.7 Earthquake input conditions

针对采用钢弹簧隔振减震装置Benchmark隔震结构模型，分别输入竖向环境激励和水平向罕遇地震波，计算上部结构的加速度和位移响应，分析装置各性能参数对结构振动控制效果的影响。

3 竖向环境激励下装置参数对隔振效果影响

3.1 结构隔振计算方程

为了研究钢弹簧隔振器的隔振效果，对建筑结构与钢弹簧隔振器构成的隔振系统进行计算。定义列车传递到支撑基础结构的振幅与隔振目标建筑物的振幅之比Td为振动传递率，则有:

(2)

(3)

式中:D为隔振系统阻尼比；为激振频率与系统固有频率之比。由式(1)可以得出当η>时，Td<1。即外部激振频率f与隔振系统的自振频率fn的关系应先满足式(3)，钢弹簧隔振器才能产生隔振效果。

F=kvX

(4)

(5)

式中:F为上部结构的竖向荷载;kv为隔振体系的竖向总刚度;X为隔振系统中隔振器的竖向压缩量;g为重力加速度值。根据式(3)设定隔振系统的频率，再根据式(4)和式(5)确定钢弹簧隔振系统中隔振器的竖向压缩量X，进而确定钢弹簧隔振器所需的竖向刚度，然后根据试验得到钢弹簧隔振器的竖向刚度，选配钢弹簧隔振器型号。结构振动为线性动力反应，动力方程[17]为

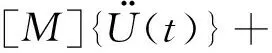
(6)

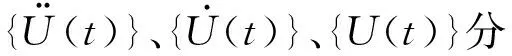
3.2 钢弹簧隔振减震装置竖向隔振效果参数分析

3.2.1 隔振器竖向参数设定

为研究钢弹簧隔振减震装置的刚度和阻尼对结构隔振效果的影响，根据隔振层设定参数计算，在Benchmark模型结构中柱底布置一定数量钢弹簧和一定规格的阻尼筒组成的隔振减震装置，计算其在C7、C8、C10、OZ1环境信号扰动下的振级响应。在刚度分析计算工况的设定中，设定隔震层阻尼比为0%，根据工程应用中刚度比常用取值范围为(2.23%～6.68%)，刚度分析工况如表8所示，其中，刚度比是隔振层总刚度与上部结构各层刚度平均值的比值。在阻尼分析计算工况的设定中，设定隔震层刚度比为4.45%，根据工程应用中阻尼比常用取值范围为(0～10%)，阻尼分析工况设定如表9所示。

表8 刚度分析工况设定Tab.8 Loading conditions of SSVI for stiffness

表9 阻尼分析工况设定Tab.9 Loading conditions of SSVI for damping

3.2.2 钢弹簧隔振减震装置竖向隔振效果分析

为研究隔振层刚度对隔振效果的影响，对隔振结构进行模态分析，水平向和竖向自振频率如表10所示。根据刚度参数分析计算结果，取结构每层中心点为结构层参考点，结构各层参考点振动加速度级反应如图17所示。由图可知，钢弹簧隔振减震装置的竖向隔振效果明显。随着隔振层刚度比的减小，各层结构的振动加速度级减小，隔振效果更好。根据(JGJ/T170—2009)《城市轨道交通引起建筑物振动与二次辐射噪声限值及其振动方法标准》的要求，城市轨道交通沿线建筑物昼间室内的振动加速度级限值为65 dB，在OZ1波激励下无控结构各层的振级都低于65 dB，环境振动隔振设计应根据结构所受到城市交通激励情况进行设计；在四种激励信号的影响下，框架结构各层振级应小于规范规定的65 dB，仅工况二计算结果满足要求，故建议钢弹簧隔振减震结构水平向刚度比小于1.67%。

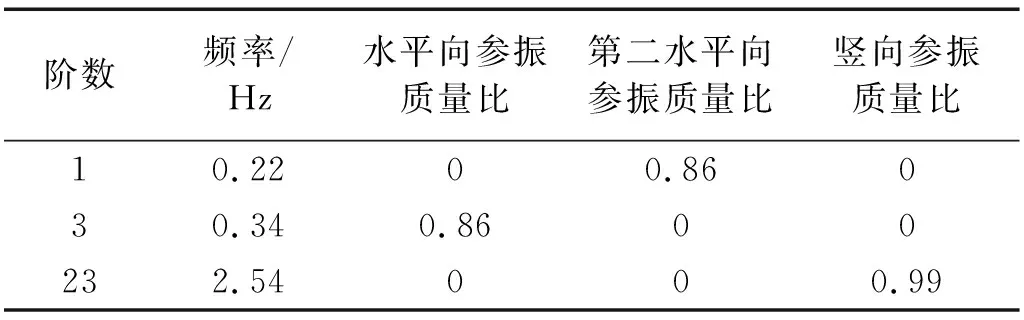
表10 模态分析Tab.10 Modal analysis

为了研究隔振层阻尼比对隔振效果的影响，根据阻尼参数分析工况的计算结果，结构各层参考点振动加速度级反应如图18所示。从图中可以看出，阻尼比对隔振效果影响很小，当隔振层阻尼比在0.02～0.12的范围内，随着钢弹簧隔振减震装置阻尼系数的增大振级反应减小，隔振效果更好。

4 水平罕遇地震下装置参数对减震效果影响

4.1 装置水平向参数设定

为研究隔振减震装置的刚度和阻尼对结构减震效果的影响，根据装置在工程中的常用范围，设定钢弹簧隔振器参数分析计算工况，表11为刚度分析工况设定，表12为阻尼分析工况设定。针对无控及配置不同钢弹簧装置参数的隔振结构，计算其在表7所示的八种地震影响下的动力响应。

表11 刚度分析工况设定Tab.11 Loading conditions in simulation for stiffness

表12 阻尼分析工况设定Tab.12 Loading conditions in simulation for damping

4.2 装置水平向减震效果参数分析

为了研究隔震层刚度比对减震效果的影响，根据刚度参数分析工况的计算结果，结构顶层加速度与隔震层位移响应峰值如图19所示。从图中可以看出，随着隔震层刚度比的增大，结构顶层加速度变大，隔震效果变差，变化主要发生在刚度比为1.7%～8.9%范围内；当刚度比在8.9%～26.7%时，结构顶层加速度峰值增速放缓；刚度比为26.7%时结构的响应基本与刚度比为8.9%时结构的响应持平。

为了研究隔震层阻尼比对减震效果的影响，根据阻尼参数分析工况的计算结果，结构顶层加速度以及隔震层位移响应峰值如图20所示。从图中可以看出，随着隔震层阻尼比的增大，结构的顶层加速度峰值变小，隔震层水平向变形减小。

为明确钢弹簧隔振减震装置在罕遇地震下的参数设计要求，根据参数分析工况的计算结果，分析上部结构层间位移与层高的比值，如图21所示，从图中可以看到，最大层间位移比随着刚度比的减小而减小，阻尼比对上部结构层间位移的影响相对较小，数据显示最大层间位移比会随着阻尼比增大而减小；GB50011—2010《建筑抗震设计规范》规定建筑结构层间位移比限值为1/50，在1#波影响下，配置钢弹簧隔振减震装置的上部结构的层间位移比都大于1/50；在2#波影响下，当隔震层刚度比为6.68%并且阻尼比为6%时，上部结构的层间位移比都小于1/50。由此可以给出抗震设计建议，当建筑抗震设计目标为罕遇九度地震时，不能使用钢弹簧隔振减震装置进行单独抗震设计，需与普通黏滞阻尼器协同进行减震控制工作；当结构抗震设计目标为八度地震时，建议结构的减震层刚度比小于6.68%，减震层阻尼比大于12%。

5 结 论

对钢弹簧隔振减震装置进行了双向性能检测试验，并对不同参数装置竖向环境激励和水平向罕遇地震结构振动控制效果进行了分析，研究得到以下结论：

(1) 装置中的钢弹簧隔振器参数稳定，灵敏度高。竖向力与变形成线性关系，水平向抗地震剪力能力强，具有较好的水平变形能力，但不具备耗能能力。钢弹簧隔振器的水平向剪切形变稳定限值为93.9 mm，屈服力为62.21 kN，钢弹簧隔振器受压剪失稳后，剪切力骤降，呈现脆性破坏。

(2) 装置中的阻尼筒在竖向和水平向都具有良好的耗能能力，由于阻尼杆和阻尼液的“黏连”能力有限，水平向阻尼系数都是随着加载频率和加载幅值的增加而减小，竖向阻尼系数随着加载幅值增大而减小，在加载频率达到3 Hz后竖向阻尼系数随着加载频率增大而减小。

(3) 在竖向环境振动激励下，钢弹簧隔振减震装置的隔振效果明显，结构各楼层的振级反应随着隔振层刚度比的减小而减小，隔振层阻尼比对隔振效果影响很小；在C7、C8、C10、OZ1激励信号的影响下，隔振层水平向刚度应小于1.67%，在仅考虑城市交通扰动时，无需设计带有阻尼筒的隔震装置。

(4) 在水平向罕遇地震影响下，不同刚度比区间下，减震装置的控制性能和变化规律是有差别；不同阻尼比区间下，减震装置的控制性能相差较小；当结构抗震设计目标为八度地震时，建议结构的减震层刚度比小于6.68%，减震层阻尼比大于12%。