厚度振动换能器降耦合结构优化与工程应用

2021-09-19 01:16李海森卞加聪

振动与冲击 2021年17期

赵慧，李海森，王艳，卞加聪，李科

(1.哈尔滨工程大学水声工程学院，哈尔滨 150001；2.上海船舶电子设备研究所，上海 201108)

压电振子的厚度振动模式是水声高频换能器的主要工作模式，在工程应用中，对压电圆片而言，横向方向的耦合作用总是存在的，不存在理想的厚度振动模式。若压电圆片的尺寸比例合适，横向耦合作用较弱，若尺寸比例不合适，横向耦合作用会很强。一方面，虽然耦合作用可以拓展换能器的工作带宽，但是却使压电振子表面的振动位移反相，降低了换能器的发射效率；另一方面耦合使得厚度振动频率附近出现多个难以区分的谐振峰，使得换能器的频率设计准确性降低。受耦合影响，某军用型号项目中的厚度振动换能器的生产质量不高，成品率低，单批次生产合格率约为50%～60%，急需开展降耦合技术研究，提升厚度振动换能器的声学性能和生产质量。

压电圆片的厚度振动模频率一般大于100 kHz以上，水声高频换能器主要利用厚度振动模工作。国内著名水声换能器专家莫喜平对高频宽带换能器技术方向的研究进展和发展做了详细论述[1-2]。目前对降耦合的相关研究论述却不多。理想压电圆片振子的厚度振动常用一维振动理论来近似处理[3]，而有限尺寸的压电圆片则必须考虑径向的耦合。早在1977年，Mori等[4]就提出了用表观弹性法来处理压电振子的耦合振动，林书玉等[5-6]利用解析法对压电圆片、压电圆环等振子的耦合振动引入等效弹性系数，推导了压电陶瓷振子多模耦合振动的等效电路及共振频率方程，李明轩等[7]还对高频厚度模换能器的应电压特性进行了分析，给出了不同负载情况下高频振荡特点。

国外，Guo等[8-10]先后用有限元法和数值分析法分析了压电振子的耦合振动模态，计算了横向耦合的纵向振动压电晶体的二阶理论。Kybartas等[11]采用有限元法分析了压电振子的横向与纵向不同比例时，各阶振动模态的机电耦合系数变化，以及不同压电材料对耦合模态机电耦合系数的影响。Jing等[12]研究了径向轴向耦合较强的圆柱体振动系统，当选择合适几何尺寸时，该振动系统能有效地辐射高功率超声。Lee等[13-15]研究了压电陶瓷圆盘径向振动的近场和远场声辐射特性，计算了具有自由边界的厚圆盘径向结构模态声辐射解析解，对压电圆片换能器径向模态产生的贝塞尔超声束进行了全面的分析和试验研究。国内外对耦合的分析大多是分析压电振子耦合特性，较少论述如何降耦合，以及减少耦合影响。本文以厚度振动压电圆片换能器为例，对降耦合开展研究，通过对理论计算、仿真分析和试验验证，获得降耦合的有效措施，为高质量厚度振动换能器的研制和生产提供技术指导。

1 厚度振动模态计算

1.1 振动频率理论计算

高频圆面活塞换能器的功能元件为压电陶瓷圆片。图1为一沿厚度方向极化的压电陶瓷圆片，直径为2a，厚度为2t，厚度方向为极化方向。

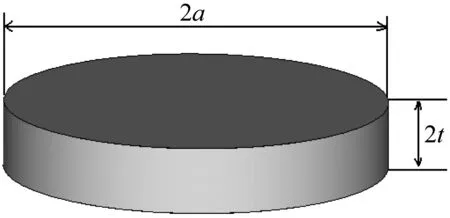
图1 压电陶瓷圆片Fig.1 Disk plates of piezoelectric ceramics

对于压电陶瓷圆片的轴对称自由振动，径向方向应力Tr与切向方向应力Tθ近似相等。

(1)

(2)

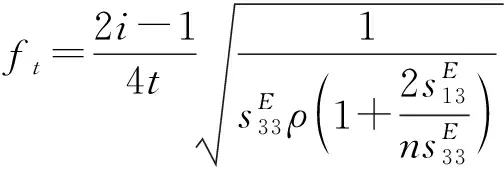
(3)

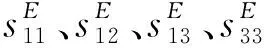
从式(1)中解出耦合系数n，代入式(2)、(3)即可求得径向高阶频率和厚度振动高阶频率。从计算公式看，考虑了耦合后，径向振动频率不仅跟材料参数、直径尺寸有关，还与厚度与直径的比有关，厚度振动频率也是同样。因此要进行降耦合研究，需要从材料、尺寸、结构形状等多方面综合考虑，才能取得满意效果。

以直径2a=60 mm、厚度2t=10 mm的PZT-4压电陶瓷圆片为例计算径向振动和厚度振动的谐振模态。将材料参数代入耦合系数方程中，解方程得出耦合系数的值为

n1=1.496，n2=-0.048

两个耦合系数的值分别对应着圆形振子的厚度振动和径向振动，计算结果如表1所示。

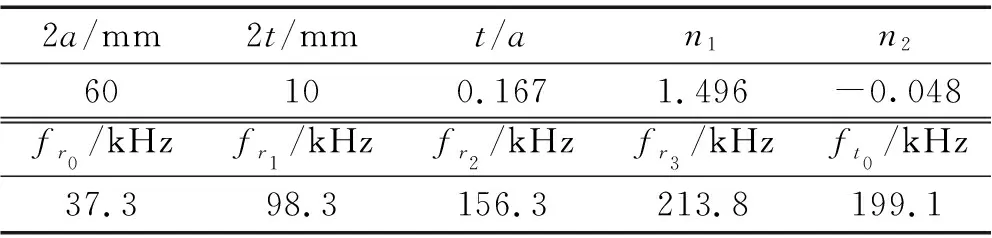
表1 振子厚度振动及径向振动的计算结果Tab.1 Theoretical results of radial vibration frequency and thickness vibration frequency

表1中的fr0、fr1、fr2、fr3分别表示径向振动的基频以及高次谐波振动频率，ft0为厚度振动基频。从计算结果可以看到，径向高阶频率与厚度振动频率相隔很近。在某军用型号工程中的一批换能器中，相隔较近的谐振频率使得换能器的电导值和动态电容值在工作频率点处存在较大的差别，要得到合格的换能器必须要从大量的换能器中挑选出相近的，致使该类换能器的生产质量和成品率大大下降。

1.2 振动模态仿真

有限元仿真软件计算压电陶瓷振子会得到很直接明了的结果，同时还能直观形象表示出换能器振子的振动形态。对上节中的同样尺寸与材料的压电振子，有限元的计算结果如表2所示。

表2 振子谐振频率仿真结果与理论计算结果对比Tab.2 Comparison of simulation results and theoretiacal calculation results

从表2中结果可以看出，径向低阶模谐振频率与仿真计算结果比较吻合，而径向高阶模的二阶和三阶的理论计算与仿真计算结果相差较大，还存在谐振频率与理论值没有对应关系的。

为了弄清厚度振动频率受到的耦合影响，需要对各谐振频率的振动模态进行辨认。

由于压电陶瓷圆片振子是轴对称模型，利用有限元软件仿真计算，建立二维轴对称模型即可。图2为压电圆片的各个谐振频率的振动模态图，圆片的极化方向为厚度方向，边界条件为自由边界。图2中(a)、(b)、(c)分别对应径向振动一阶、二阶和三阶谐振频率。(d)、(e)、(f)、(g)、(h)、(i)、(j)均为耦合振动模态，是在低于或接近厚度振动谐振频率范围内各谐振频率对应的模态振型图。单从模态振型图上很难准确判断各个谐振频率对应的振动模态，它们叠加了径向的高阶振动模态、厚度伸缩振动模态、厚度剪切振动模态、弯曲振动模态、扭转振动模态等。综合理论计算、模态振型图以及厚度伸缩振动特点分析，其中(i)振动模态最接近厚度振动模态，是以厚度振动模态为主的耦合振动模态。

图2 振动模态图Fig.2 Vibration mode diagram

厚度振动模态是水声高频换能器常用的振动模态，在分析厚度振动模态时，经典的一维理论计算模型要求横向尺寸远远大于纵向尺寸，本文采用的理论计算模型虽然没有此要求，但也忽略了厚度剪切振动模态、弯曲振动模态等，仅考虑了径向模态的耦合，计算得到径向的低阶模态与有限元结果较吻合，而高阶模态与实际接近的有限元仿真结果具有较大的偏差。由于厚度振动模态叠加了很多耦合模态，从理论模型上进行降耦合计算分析，变得非常困难。因此后续章节将采用有限元方法进行换能器参数的计算，以期使计算分析的结果具有指导性。

2 几何参数对振动模态频率的影响

压电材料的特性、压电元件的尺寸以及结构形状等均会对耦合的强弱产生影响。考虑工程上常以PZT4材料作为高频发射换能器主要功能元件，材料特性是固定的，本文不将其作为研究对象。本文主要分析压电元件的尺寸和结构形状对耦合的影响。

由于耦合的复杂性，压电元件的任意一个方向的尺寸均会产生谐振特性，叠在一起形成非常复杂的耦合模态。以压电圆片为例，当厚度尺寸小于径向尺寸时，压电圆片呈细长棒形状，有纯净的纵向振动；当压电圆片的厚度尺寸远大于径向尺寸时，在厚度振动频率附近，厚度振动模态为主要模态，径向及其他的耦合模态也会存在，但对厚度振动模态的影响较少，主要表现为厚度振动模态；当两个尺寸可比拟时，如2a/2t=1～10以内时，厚度振动模态受到耦合影响较为强烈。

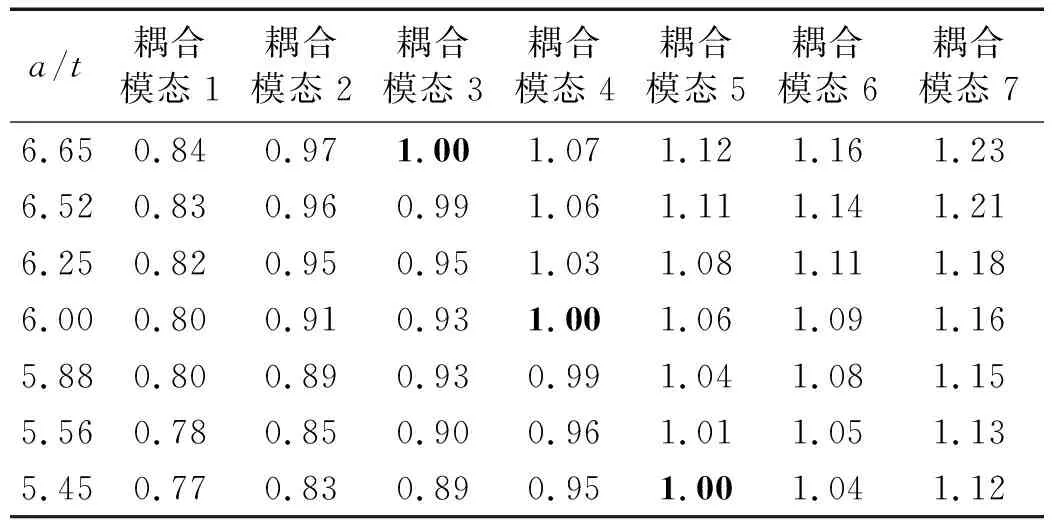
2.1 直径变化对厚度振动频率的影响

从振动模态图分析，可知在厚度振动频率处，受耦合影响最大的主要是径向的高阶模态，固定厚度2t，变化直径2a，研究当2a/2t在不同比值时，厚度振动频率的变化情况。

表3中的数值是在固定厚度t，改变直径a，仿真计算得到的谐振频率与厚度振动基频的比值。分析可得结论：① 随着a/t值的增加，厚度振动频率附近会出现越来越多的耦合谐振峰，并且各耦合谐振峰相隔越来越近，最终收敛于厚度谐振频率；② 当a/t<1.9时，无法得到厚度振动频率，径向耦合模态非常强，谐振频率均小于厚度振动频率；③ 当1.9≤a/t≤3.6时，厚度振动频率附近的耦合频率与厚度振动频率相隔10%以上，此时径向方向的耦合对厚度谐振频率耦合影响较少；④ 当3.6