空间敏感载荷用超精密驱动系统刚柔耦合振动分析

孙小庆， 杨斌堂， 柏 转， 忽 伟

(1.东华大学 机械工程学院，上海 201620； 2.上海交通大学 机械系统与振动国家重点实验室，上海 200240；3.上海航天控制技术研究所，上海 201109)

空间望远镜、激光通信卫星及其它光学仪器等敏感载荷在轨运行过程中对定位精度具有很高的要求[1]。采用电机丝杠的驱动系统方案尽管同样具备实现微纳米精度的能力，但其结构尺寸较大、附加质量过重及传动部件存在摩擦、磨损并需后期润滑维护等因素影响了其在航天领域的进一步应用[2]。面向未来深空探索的重任，以小型化、集成化设计理念为指导[3]，采用新型智能材料以“直接驱动”型式进行作动的方案是当前研究的一个热点[4]。

为此，本文提出了采用超磁致伸缩材料作动结合柔顺放大机构的超精密驱动系统方案。作为实现对智能材料作动器输出位移进行放大的核心部件，柔顺放大机构不仅承担着运动传递的功能，同样还需满足一定的放大功能。直观上，柔顺放大机构利用材料自身的弹性变形来实现对运动的传递[5]，其结构柔度越大，越有利于运动的传递和缩放。然而，负面影响则是在作动器驱动下产生大范围刚性运动过程中容易诱发柔性部件的弹性振动，从而影响驱动系统的精度。

对当前柔顺机构的弹性振动问题，研究主要集中在对典型的单悬臂梁进行刚柔耦合建模与分析，进而实现对弹性振动的抑制方面。陈特欢等[6]针对柔顺宏微操作器中悬臂的微纳振动问题进行了最优抑振轨迹的规划，实现了弹性振动幅值52.2%的减小。张清华等[7]则研究了利用闭环控制策略对平面柔顺并联机构运动过程中产生的弹性振动的抑制问题。张泉等[8]则详细研究了3-PRR柔性并联平台的刚柔耦合问题，并对柔性振动进行了主动控制研究。上述研究为具有较高作动带宽的柔顺机构所产生的弹性振动提供了可行的抑制策略，但是对以位移缩放为主要功能的柔顺多级放大机构及其在受限频带内的刚柔耦合问题的研究却尚未见诸报端，此外对放大机构柔性振动对刚体运动的具体影响程度也缺乏足够的分析与认知。考虑到当前研究刚柔耦合振动问题的手段大多以有限元分析软件，如ANSYS、ABAQUS等与ADAMS进行联合模拟[9-10]，故而较难从理论上对刚柔耦合产生的机理以及相关参数对柔性振动的影响程度进行充分的研究。

因此，针对空间敏感载荷的超精密定位问题，本文首先提出了一种基于智能材料作动器和柔顺放大机构的超精密驱动系统方案。随后，建立了柔顺放大机构的刚柔耦合动力学模型，通过数值仿真研究了柔顺放大机构在作动频带内的弹性振动问题。最后通过原型样机试验，证明了所提系统方案的可行性。该方案能为航天敏感载荷提供一种可行的、小型化、集成化的精密驱动型式。

1 超精密驱动系统方案设计

空间望远镜、激光通信卫星等敏感载荷在工作过程中需要满足特定的精度需求。考虑当前航天设备的小型化、集成化发展趋势，利用电机丝杠方式实现进动不仅结构尺寸较大、而且精度也因各传动环节的累积误差而受到限制。为此，本文提出了以智能材料作动器结合柔顺放大机构的超精密驱动系统方案，方案具体如图1所示。

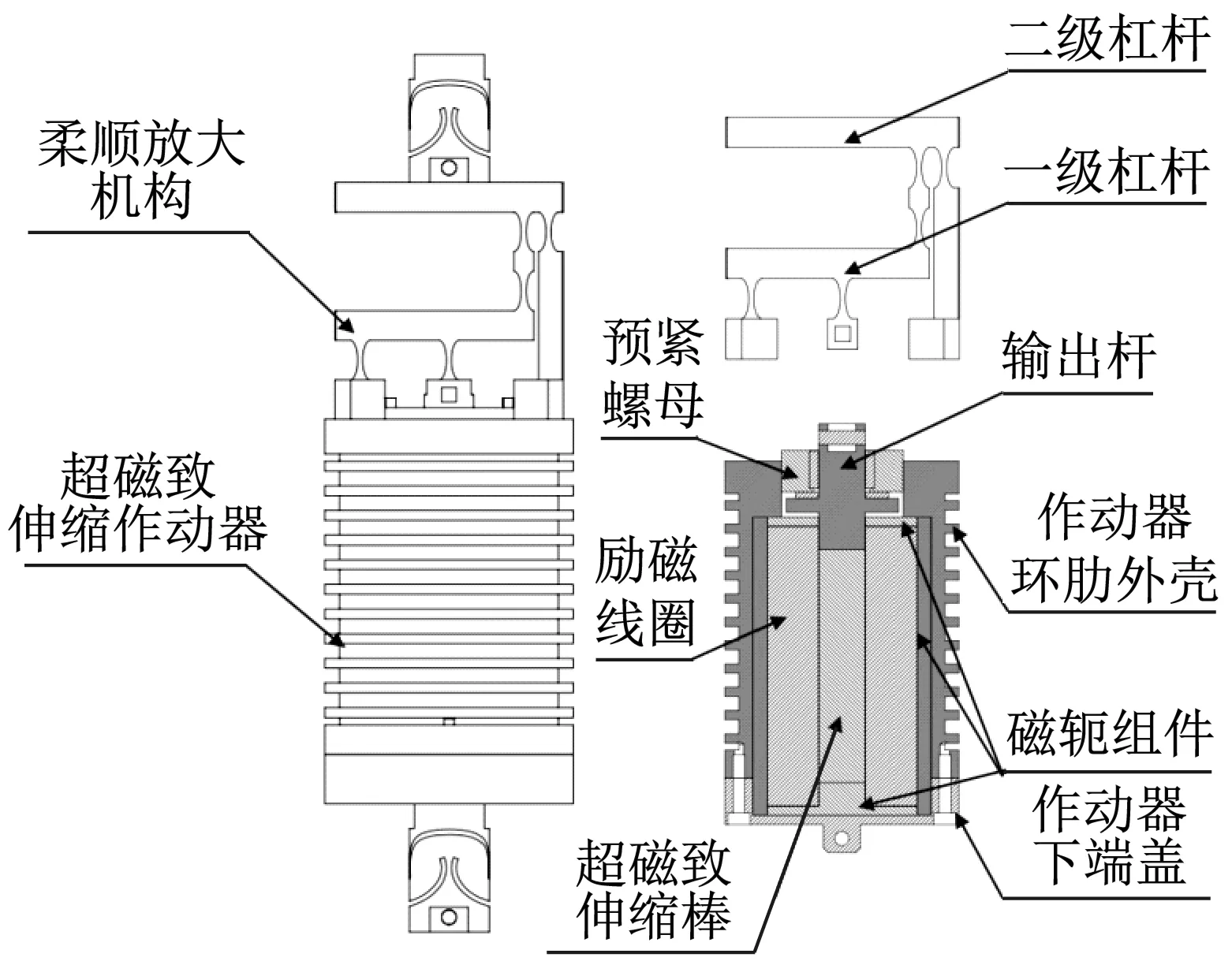
图1 超精密驱动系统Fig.1 Scheme of the ultra-precision driving system

鉴于空间敏感载荷的作动频率通常较低，而磁致伸缩材料相比智能压电材料而言具备更优异的低频特性[11]，且其无须高压驱动等机理都更适用于空间环境，故该方案将采用超磁致伸缩作动器来实现初级作动位移的输出。考虑利用柔顺放大机构来实现对作动器输出位移的放大，不仅满足了亚毫米输出行程的需求，同时还利用了其能有效减少构件数量及无摩擦磨损和传动间隙等优点[12]。超磁致伸缩作动器利用励磁线圈产生磁场，从而直接促使智能材料棒体发生形变，进而推动输出杆对外做功。输出杆进一步推动柔顺放大机构一级杠杆和二级杠杆，以实现最终位移的放大输出。整个过程涉及的主要零部件包括：超磁致伸缩棒、励磁线圈、磁轭组件、输出杆、预紧螺母、作动器环肋外壳、作动器下端盖以及柔顺放大机构。

该驱动系统可近似视为是“零传动”系统，屏蔽了传统机械部件所存在的摩擦、磨损及滞回等问题，从而能够使超磁致伸缩驱动器的高分辨率输出位移得以最大程度的保留。对柔顺放大机构而言，其通过线切割方式在整块材料上一体化加工而成，通过利用材料本身的弹性变形来实现运动的传递，能够有效避免实体铰链因间隙问题导致的传动误差，同时还有利于集成设计的实现[13]。然而，柔顺放大机构也存在因受外界驱动而发生弹性变形振动从而引发最终输出位移波动而降低输出精度的问题。因此，接下来建立柔顺放大机构的刚柔耦合动力学模型以研究其动力学特性、进而反向论证其结构设计参数。

2 柔顺放大机构刚柔耦合建模

基于上述分析，考虑柔顺放大机构为典型的刚柔耦合系统。两级柔顺杠杆做大范围刚体运动的同时，会诱发自身的小弹性变形运动，此两种运动相互耦合、互为影响。综合利用伪刚体模型法、假设模态法和Lagrange方程在垂直平面内建立柔顺放大机构的动力学模型，如图2所示。

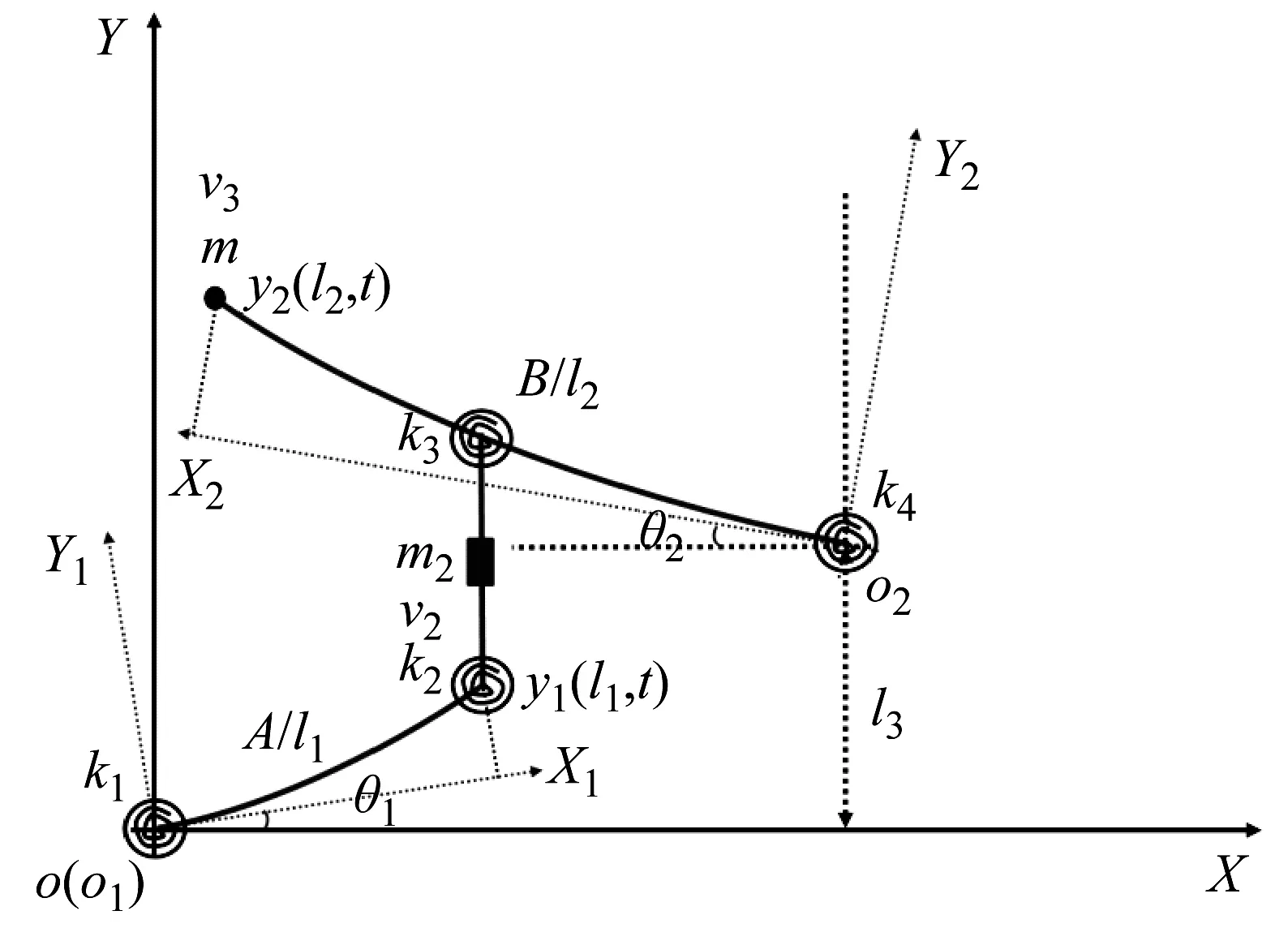
图2 柔顺放大机构刚柔耦合模型Fig.2 Rigid-flexible coupling model of compliant amplifier

两柔顺杠杆采用切线坐标法进行位移描述[14]，然后基于混合坐标建模理论推导其动能、势能。坐标系O-XY为惯性系，O1-X1Y1、O2-X2Y2分别为固定在两柔顺杠杆上的浮动坐标系。同时做如下假定：中间连杆较短，可视为刚性杆件，长为l3，其运动只发生在垂直方向上，等效质量为m2；两柔顺杠杆A、B长分别为l1和l2，密度分别为ρ1和ρ2，截面积分别为A1和A2，抗弯刚度分别为E1I1和E2I2；柔性铰链可等效为具有一定刚度的扭簧，刚度分别为k1,k2,k3,k4；两柔顺杆的大范围运动角位移分别为θ1和θ2，认为近似存在如下关系θ2=λθ1；两柔顺杆均采用Euler-Bernoulli梁假设，忽略两杆件的纵向变形和重力影响。

令(x1,y1)、(x2,y2)分别为A、B两杆上任一点在各自连体系中的坐标，可推导出在惯性系下的绝对坐标，对A杆有

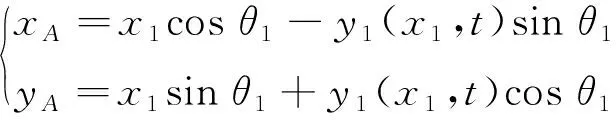
(1)

对B杆有

(2)

因此，对A杆上任一点坐标求导，得其速度向量为

(3)

对B杆上任一点的坐标求导，得其速度向量

(4)

因此，系统的动能可表示为

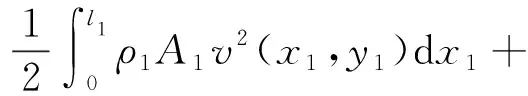
(5)

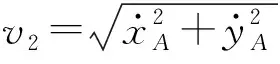
系统势能可推导为

(6)

式中，假定弹性变形相对柔顺杆件的长度而言较小[15]，则弹性变形在杆件末端的转角可计算为

(7)

作用于系统的虚功为

δW=τdθ1

(8)

式中:τ为超磁致伸缩作动器输出到柔顺放大机构上的扭矩；dθ1为刚性运动的虚角位移。

利用假设模态法，两柔顺杆在各自浮动坐标系上的横向位移可用模态坐标与模态函数的积表示，即

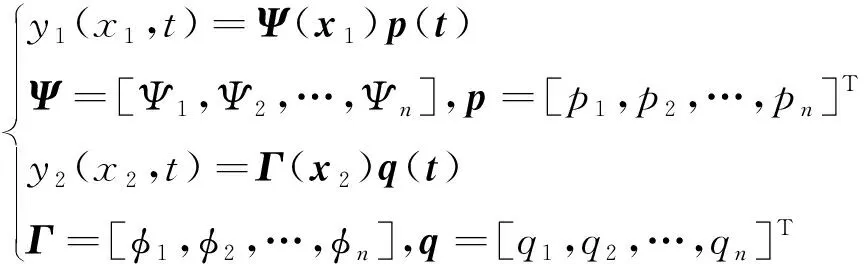
(9)

式中:Ψ∈1×n和Γ∈1×n均为n维的模态函数行向量；p∈n×1和q∈n×1均为n维模态坐标列向量；n为所选取的模态坐标个数。

联立上述方程，利用Lagrange方法推导系统的动力学模型，得到以矩阵形式表示的非线性动力学模型为

(10)

式中，广义质量矩阵、广义刚度矩阵和非线性耦合矩阵的各参量表达式经推导得到。进一步分析发现，该柔顺放大机构的动力学方程是典型的耦合非线性微分方程组，为了实现上述方程的求解，需要转换到状态空间，使其成为一阶微分方程组[16]，经变换后的方程组为

(11)

根据柔顺放大机构与超磁致伸缩作动器的实际装配情况，在研究中，两柔顺杆件可采用一端铰支，一端自由的梁作为假设模态。则两等效梁的振型函数可表示为[17]

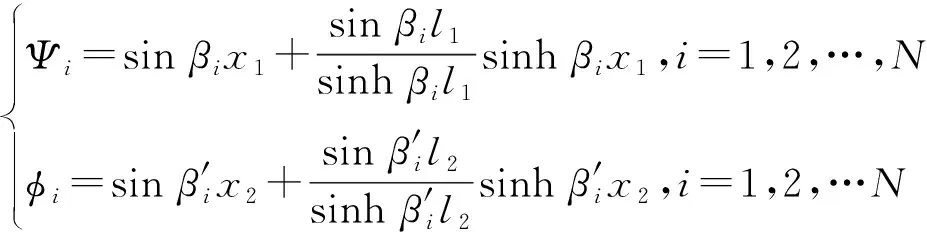
(12)

式中，与振型有关的参数可取

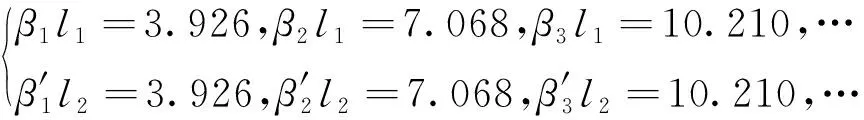
(13)

3 刚柔耦合振动特性仿真分析

根据上述推导的动力学模型进行柔顺放大机构的刚柔耦合仿真分析。由于整个柔顺放大机构采用相同的材料，同时两柔顺杆件的横截面积和密度也采用了相同的设计。对各柔性铰链，其结构参数也保持一致，因此具有相同的转动刚度。仿真研究中相关参数如表1所示。

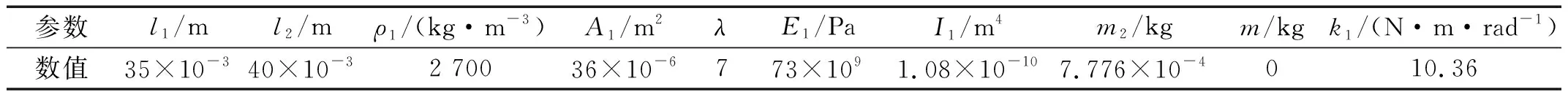
表1 仿真参数Tab.1 The simulation parameters

为便于研究柔顺放大机构在杠杆A受到作动器驱动作用下，柔顺放大机构整体的运动输出状况以及引起的输出杠杆B的弹性变形振动，可以选择施加单位驱动力矩进行数值计算，施加的力矩变化规律如下

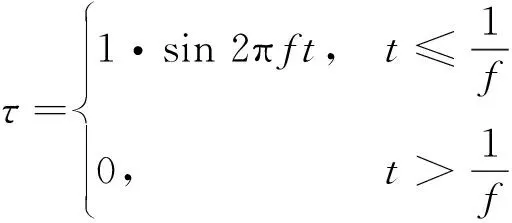
(14)

式中，f为驱动力矩频率。该公式表明，在运动开始的第一个周期时间内，杆件A受到一个周期的正弦力矩，一个周期后驱动力矩为零，之后系统自由振动。若两杆为刚性杆件，则此时两杆速度均为零，呈静止状态。但考虑两杆均为柔顺杆件，则在运动过程中存在弹性变形运动，当驱动力矩消失后，可以预见杆件的弹性振动将因系统的无阻尼状态而持续振动下去。

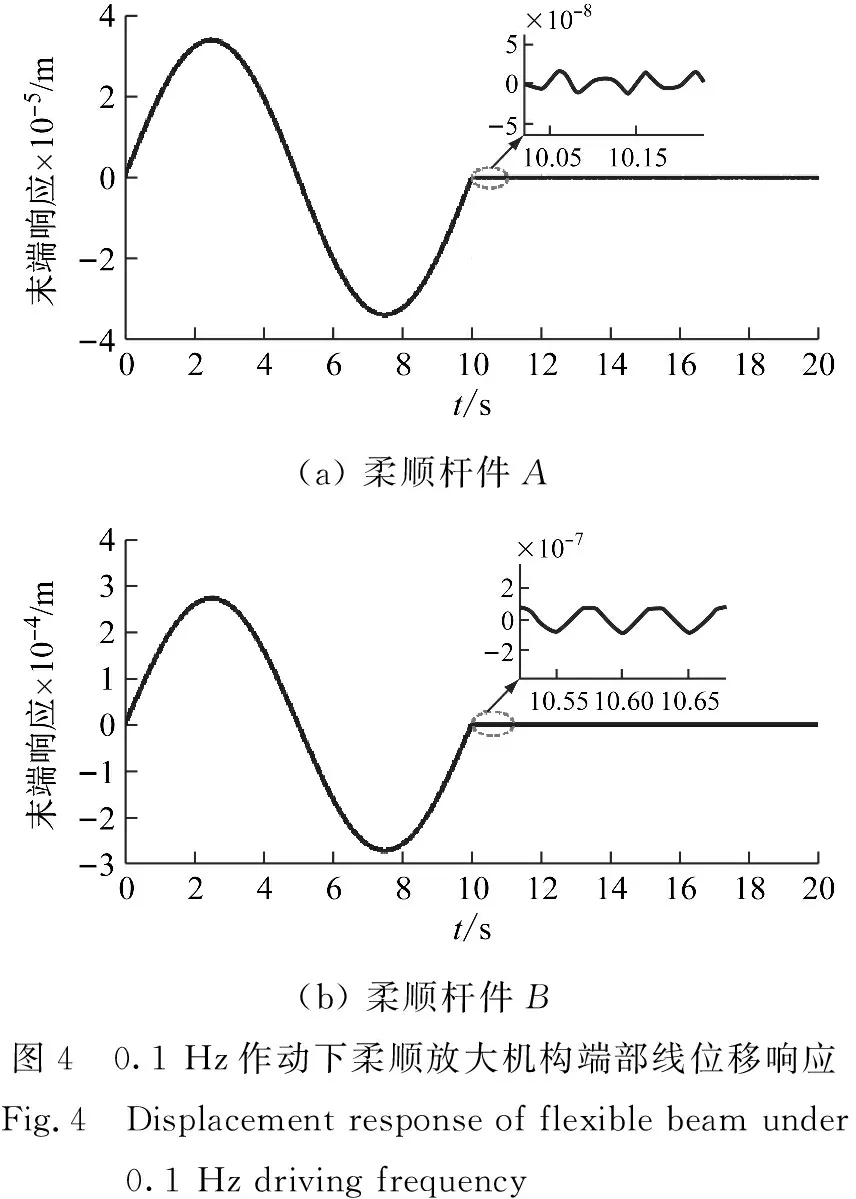
鉴于空间敏感载荷的超精密作动带宽在5 Hz以内，因此通过Matlab编程计算了频率分别取0.1 Hz,1 Hz,5 Hz和10 Hz时，柔顺放大机构的末端响应特性。仿真时间设置为20 s，计算结果如图3所示。

根据图3、图4可知，在0.1 Hz的作动输入下，柔顺放大机构在前10 s呈现了明显的刚体运动响应；在驱动力矩消失后，两柔顺杆件均产生了弹性振动，由于忽略了阻尼，该弹性振动将持续下去；对柔顺放大机构输出杆B而言，在单位力矩作用下，刚柔耦合产生的柔性振动幅值仅为2×10-7m，与刚体运动的幅值比仅为0.04%。因此，基本可以忽略柔顺放大机构因刚体运动引起的柔性振动。

进一步分析在不同驱动频率下柔顺放大机构末端输出杆件的刚柔耦合振动特性，分析结果如图5所示。

根据上述仿真结果，可以发现随着作动频率的增加，杆件B末端刚体响应幅值基本保持不变，但弹性振动有加剧趋势。进一步整理各作动频率下放大机构输出杆B对应端部的动态响应幅值，统计结果如表2所示。

表2 仿真结果Tab.2 The simulation results

分析表2发现，在驱动单位力矩频率从0.1 Hz～10 Hz变化过程中，柔顺梁B的转角位移与末端输出位移，整体幅度变化并不大，但刚性运动诱发的弹性角位移以及末端弹性输出线位移均有增大趋势。基于末端的位移输出可知，弹性振动位移幅值逐渐增大，占比也逐渐增加。当驱动频率为10 Hz时，弹性振动幅值比达到0.72%，这说明在敏感载荷所需工作频带，因超磁致伸缩作动器驱动诱发的柔顺放大机构弹性振动幅值较小，基本对刚性运动无影响，所设计的超精密驱动系统参数较为合理。

4 试验分析与验证

根据上述研究，为进一步论证在作动频带内柔顺放大机构被诱发的弹性振动对刚性输出基本无影响的结论，本节设计加工了原型样机并搭建了试验测试系统。参见图6，主要包括测试用电脑、功率电流源、信号发生器、光学隔振平台、虎钳以及基恩士激光位移传感器。光学隔振平台用于隔离外界振动干扰，虎钳用于加持原型样机。信号发生器调制所需的驱动信号，经功率电流源放大输出给超精密驱动系统，利用位移传感器采集柔顺放大机构最终端的输出响应，并通过测试电脑实时显示与存储采集到的相关信息。

图6 试验测试系统Fig.6 The experimental test system

试验时，利用信号发生器分别输入频率为0.1 Hz、0.5 Hz、1 Hz和5 Hz，峰峰值恒为16 A的正弦信号，然后经功率电流源输入给驱动系统的励磁线圈，最后对激光位移传感器采集到的试验数据进行整理，结果如图7所示。

图7 驱动系统输出响应Fig.7 Response displacements of the integrated system

根据图7分析发现，设计的超精密驱动系统在开环测试条件下，在作动频带内输出位移曲线较为平滑，无局部波动，这说明刚性运动诱发的柔顺放大机构弹性振动并不显著，弹性振动对整体刚性输出位移几乎无影响，这与仿真结论相符。进一步分析各作动频率下的响应幅值，最大可达220 μm，表明所提出的系统方案具备了亚毫米级的输出能力。同时，由于超磁致伸缩作动器自身所具有的磁滞特性，其最终位移输出曲线并非标准正弦；另外受磁轭组件涡流损耗影响，其高频输出能力受到一定限制。因此，为满足超精密作动需求，在实际工作频带，通常需采用闭环控制策略进行精密作动。

进一步对测试得到的5 Hz输出位移曲线进行频谱分析，通过MATLAB处理得到的曲线如图8所示。由图8可知，5 Hz主峰对应的即是系统的刚性输出响应；同时，在15 Hz、25 Hz出现了微小的峰值，这说明在该作动频率下，柔顺放大机构出现了一定的倍频现象，但是其幅值相比刚性运动而言，极其微小；同样地，并未观测到柔顺放大机构产生弹性振动，这说明在作动带宽内，柔顺放大机构并未因刚性运动而产生幅值明显的柔性振动，从而无法被0.5 μm分辨率的传感器测得，从而证实可以忽略柔顺放大机构产生柔性振动对系统输出性能影响的结论，从而再次论证了所设计方案的合理性。

图8 5 Hz输出位移频谱Fig.8 The displacement spectrogram in 5 Hz

5 结 论

本文针对空间敏感载荷的精密定位需求，提出了采用智能材料作动器与柔顺放大机构的超精密驱动系统方案，并对方案进行了详细的设计；随后建立了柔顺放大机构的刚柔耦合动力学模型，研究了作动带宽内柔顺放大机构的弹性振动特性，在最大驱动频率下，弹性振动与刚体运动的幅值比仅为0.61%，得到可以忽略该弹性振动的结论；最后加工实现了原型样机并搭建了试验测试系统，测试了作动频带内的系统输出性能，进一步证实可以忽略柔顺机构弹性振动的结论，试验数据同时表明所提方案初步具备了超精密作动的潜力。