基于小波技术的曲面边界光顺及简化算法

何 川，赵 罡，王爱增

(1.北京航空航天大学机械工程及自动化学院，北京 100191；2.北京航空航天大学虚拟现实技术与系统国家重点实验室，北京 100191)

自由曲线曲面在计算机辅助设计(computer-aided design，CAD)和计算机辅助制造(computer aided manufacturing，CAM)中发挥着重要作用[1-4]。其中，非均匀有理 B 样条(non-uniform rational B-splines，NURBS)已成为CAD 中表示产品几何外形的标准形式。相比于网格建模，NURBS 曲线曲面具有较好的参数连续性与光顺性，其在3D 建模等领域应用广泛。基于对有理曲线曲面的细分区间估计[5]，LI 等[6]提出了一种基于GPU 的NURBS 曲面自适应细分方法，与基于CPU 的方法相比，算法性能有了明显提高，便于实时渲染复杂的NURBS模型。DBSCs (disk B-spline curves)是一类扩展的B样条曲线，近年来，AO 等[7]提出了求DBSCs 之间所有二维相交区域的方法，为DBSCs 在计算机二维动画领域的广泛应用提供了理论基础。文献[8-10]关于NURBS 正则曲线曲面[11]的理论也为曲面变形、计算机动画提供了潜在的应用基础。

遗憾的是，B 样条曲面只能在矩形网格上定义(图1)。控制顶点的矩形拓扑结构使得B 样条曲面具有一定的局限性，特别是在处理局部细分、曲面拼接和设计的灵活性方面(图2)，具有很大挑战。针对这些问题，SEDERBERG 等[12-13]提出了T 样条的概念，在NURBS 的基础上进行了改进，且仍与NURBS 系统兼容。与B 样条曲面不同，T 样条曲面可以定义在非矩形拓扑结构上(图3)，允许T 型节点、L 型节点甚至I 型节点。非矩形拓扑结构使得T 样条曲面比B 样条曲面具有更多优势，在局部细分、数据压缩和曲面拼接(图4)时更加方便。

图1 B-mesh 拓扑结构 Fig.1 B-mesh topology

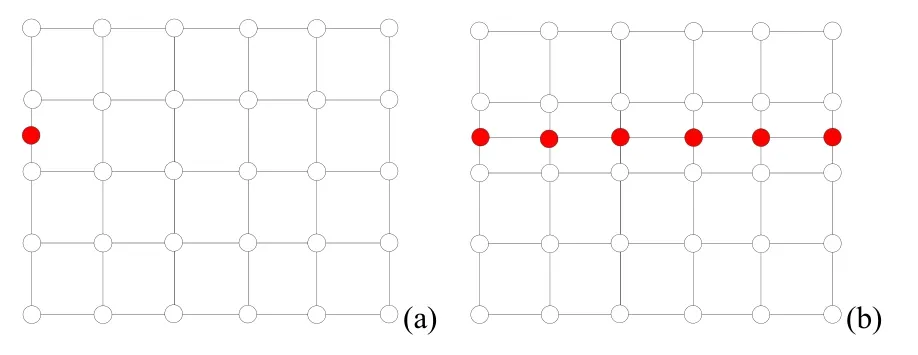
图2 B 样条曲面的局部加细((a)插入一个控制点；(b)最终的矩形拓扑结构) Fig.2 Local refinement of B-spline surfaces ((a) Inserting one control point;(b) The final rectangular topology)

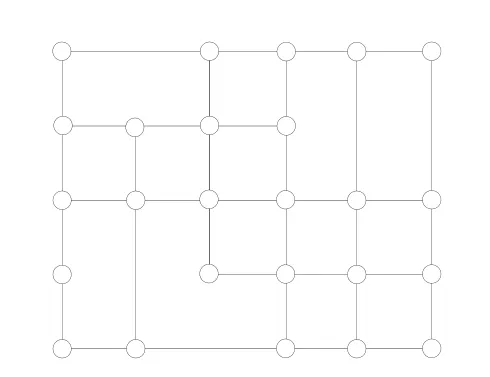
图3 非矩形拓扑结构 Fig.3 Non-rectangular topology

图4 T 样条曲面的局部加细((a)插入一个控制点；(b)最终的非矩形拓扑结构) Fig.4 Local refinement of T-spline surfaces ((a) Inserting one control point;(b) The final non-rectangular topology)

小波分析是一种数学工具，具有良好的滤波特性，在信号和图像处理以及计算机辅助设计等领域都有着广泛地应用。其中，非均匀B 样条小波常被用于曲线和曲面的多分辨建模与几何处理中[14-18]。参考文献[15]构造了非均匀B 样条小波，并给出了相应的分解和重构算法。非均匀B 样条小波基于非均匀节点矢量，可直接用于NURBS 曲线曲面的建模和编辑。

在CAD 中，边界区域对整体造型的形状有着重要影响，在产品设计中需要首先对边界区域的形状进行良好地控制。在交互设计中，设计者希望将注意力集中在局部边界区域的形状上，而保持其他部分形状不变。然而，根据矩形拓扑结构[14,16-18]的要求，基于B-mesh 的曲面边界光顺方法通常包含冗余控制点(图5(c))，且一些控制点对几何形状没有实质性贡献。如何减少NURBS 曲面边界光顺时包含的冗余控制点成为亟待解决的问题。

本文利用非矩形拓扑网格和B 样条小波，提出了一种基于T-mesh 的曲面边界光顺算法。与文献[14]和[16-18]方法相比，新算法经过曲面重构形成的T样条曲面(图5(d))，在光顺后具有更少的控制点。

图5 曲面边界光顺((a)初始B-mesh；(b)选定的一条边界；(c)传统方法的边界光顺；(d)基于T-mesh 的边界光顺) Fig.5 Surface boundary shape fairing ((a) Original B-mesh;(b) Selected one boundary part;(c) Boundary fairing by traditional methods;(d) Boundary fairing based on T-mesh)

1 B 样条小波分解技术

1.1 传统小波变换

与经典的傅里叶变换相比，传统小波变换是对空间/时间频率的局部化分析，利用二进伸缩与平移，对函数进行多尺度细化。小波分析的基本思想是将给定的尺度空间用一个低分辨空间VL-1(尺度空间)和一个高分辨空间WL-1(小波空间)表示。传统小波性质如下：

1.2 B 样条小波分解

与传统小波变换相比，B 样条小波是广泛应用于CAD 领域的新型小波变换技术。

d次B 样条曲线为

其中，Ci(0≤i≤n)为B 样条曲线的控制点；Ni,d(t) (0≤i≤n)为节点矢量t定义的d次B 样条基函数。

根据文献[15]，构造非均匀B 样条小波步骤如下：

(1) 选择初始尺度空间VL；

(2) 在尺度空间VL内定义任意2 个函数的内积；

(3) 选择子空间VL-1和小波空间WL-1。

本文假定

通过B 样条小波分解[15]，式(2)定义的曲线可以表示为

图6 给出了具有34 个控制点的三次非均匀B样条Face-shape 曲线对应的B 样条小波分解结果。经过一次B 样条小波变换，得到了仅含12 个控制点的光顺曲线，如图6(c)和(d)所示。由光顺前后曲线的曲率梳可知，B 样条小波分解不仅减少了曲线的控制点个数，而且优化了曲线的曲率分布。

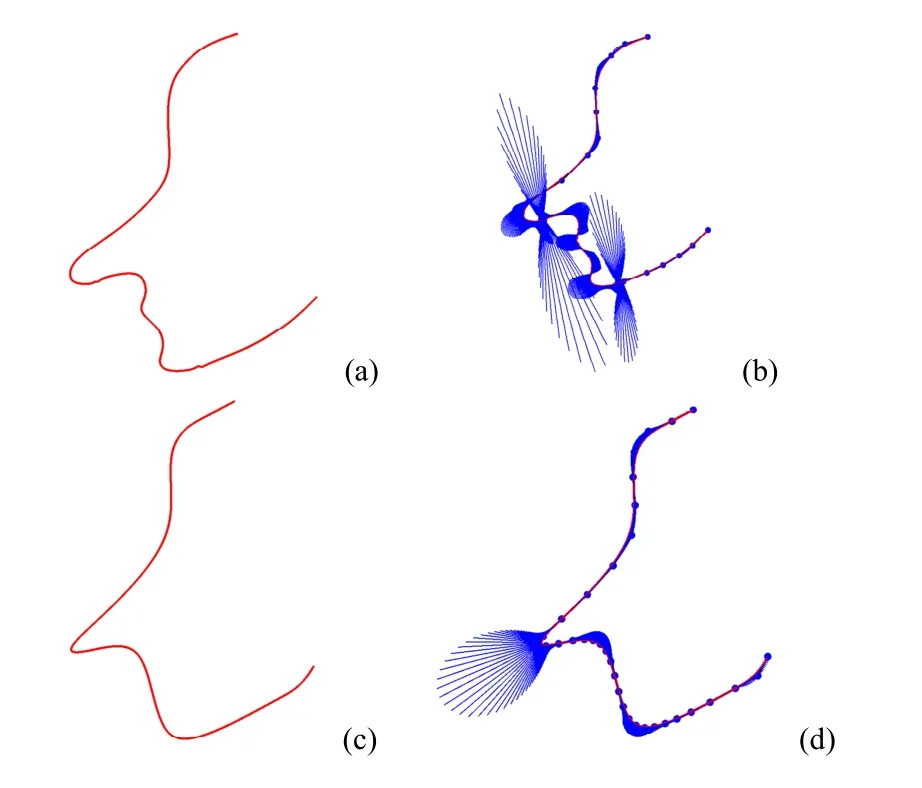
图6 Face-shape 曲线((a)原始曲线；(b)原始曲线对应的曲率梳；(c)光顺曲线；(d)光顺曲线对应的曲率梳) Fig.6 Face-shape curve ((a) Original curve;(b) Associated curvature comb;(c) Fairing curve; (d) Associated curvature comb)

1.3 T 样条技术

与NURBS 相比，T 样条曲面在局部细分、曲面拼接和数据压缩等方面具有优势[10-11]。T 样条曲面定义在非矩形拓扑结构的T-mesh 上(图7(a))，并允许T 型节点和L 型节点[10-11]。本质上，B-mesh是一种特殊的T-mesh。

d次T 样条曲面可表示为[10-11]

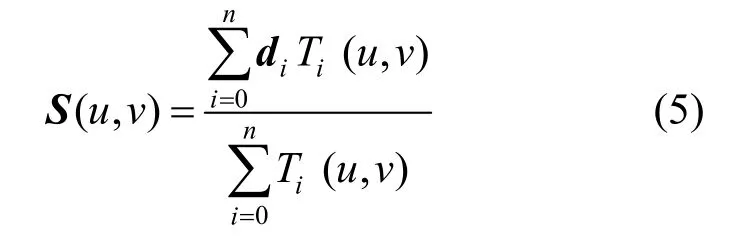
其中，di为控制点；Ti(u,v)为di对应的调配函数。与NURBS 曲面不同，T 样条曲面的调配函数可以从T-mesh 的局部拓扑结构推断出来(图7(b))，即

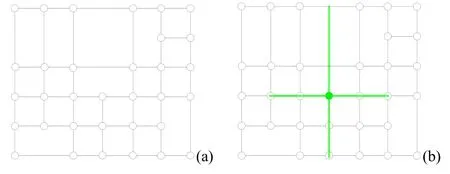
图7 T 样条曲面的拓扑结构及调配函数 ((a) T-mesh 拓扑结构；(b) T 样条调配函数) Fig.7 The topology and blending function of T-spline ((a) T-mesh topology;(b) T-spline blending function)

其中，Ni(u)和Ni(v)为B 样条基函数，根据特定的规则，其对应的节点矢量依赖于T-mesh 拓扑结构[10-11]。

2 NURBS 曲面边界光顺及简化算法

对NURBS 曲面边界进行光顺，重建一个非矩形拓扑结构的T 样条曲面，算法流程如图8 所示。对于给定的原始NURBS 曲面，选取待光顺的边界区域，并利用非均匀B 样条小波进行分解，保留尺度部分，随后通过T 样条技术对结果进行简化，得到最终的非矩形拓扑结构的曲面。

图8 曲面边界区域光顺及简化算法 Fig.8 Fairing and simplification algorithm of surface boundary shape

NURBS 曲面边界光顺及简化的过程步骤如下：

步骤1.给出原始曲面(图9)；

图9 原始曲面 Fig.9 Original surface

步骤2.选择原始曲面的边界区域(图10)；

图10 边界区域选择 Fig.10 Selected boundary shape topology

步骤3.对原始边界区域进行B 样条小波分解(图11)；

图11 边界区域的小波分解((a)原始拓扑结构；(b)尺度部分拓扑结构) Fig.11 Wavelet decomposition of the boundary shape ((a) Boundary shape;(b) The scale part by wavelet decomposition)

步骤4.通过T-mesh 重建曲面(图12)；

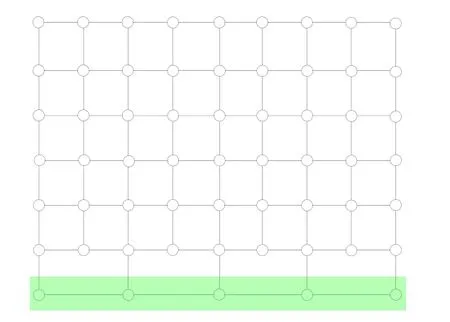
图12 光顺及简化后的边界区域 Fig.12 The final result with the faired and simplified boundary shape

与文献[14]和[16-18]算法相比，本文新算法允许存在非矩形拓扑结构的T 样条曲面，其大大减少了曲面边界光顺之后的控制点个数。对于传统文献[14]和[16-18]方法，边界区域可以进行局部光顺，但边界区域的控制点个数不能减少，由于这些方法要求曲面具有矩形拓扑结构，因此无法获得边界区域的数据简化。

3 实 例

通过2 个例子来说明本文算法的优势。例1 是Column-shape 曲面，其为三次B 样条曲面，有441个控制点。图13(a)中的红色实线是选择的边界部分，绿色实线是对应的曲率梳。由光顺前后边界曲线的曲率梳(图13(a)和(c))可知，光顺后的边界曲线，曲率单调段数比原始曲线要少得多。本文算法将原始曲面的边界曲线变得更加光顺，且含12 个控制点(图13(a)～13(d))。

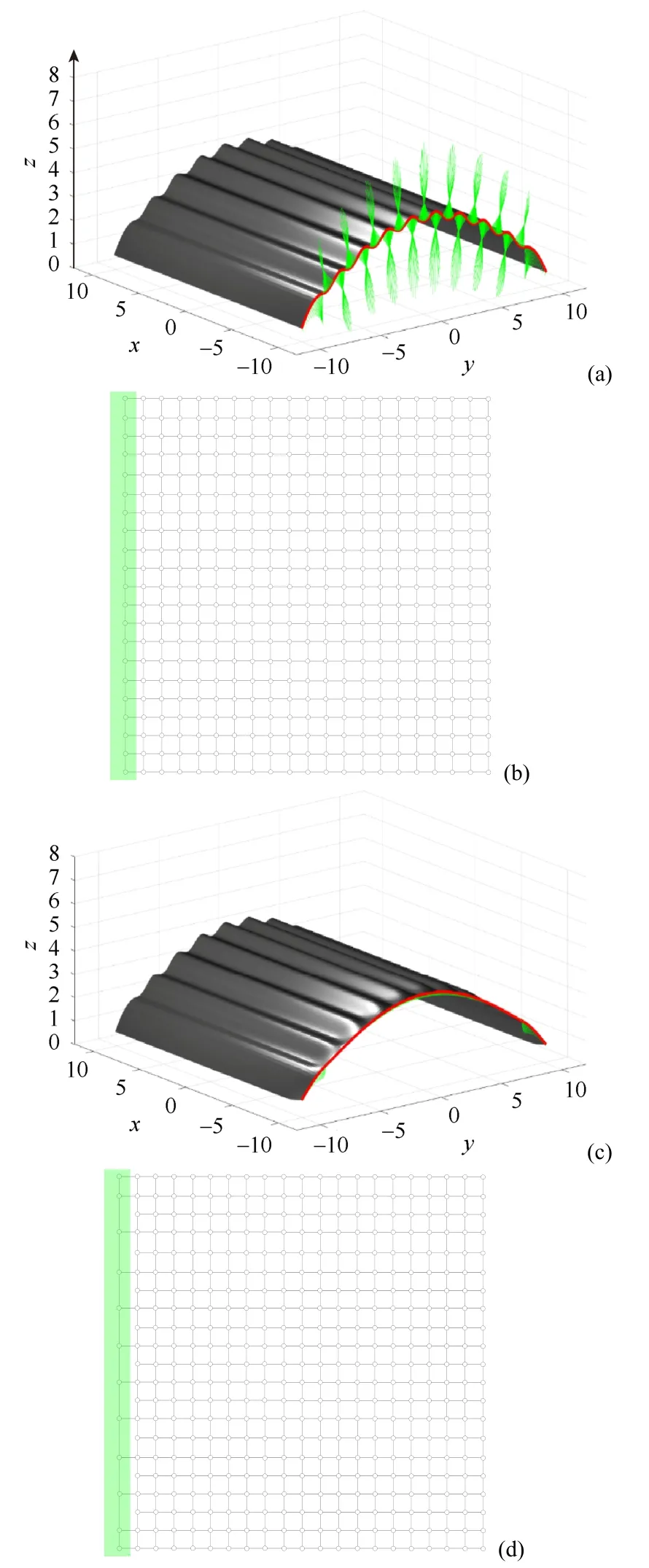
图13 Column-shape 曲面的边界光顺及简化 ((a) Column-shape 曲面。原始边界曲线(红色实线)有21 个控制点，绿色实线是对应的曲率梳；(b)原始拓扑结构；(c)用本文算法进行边界光顺。光顺边界曲线(红色实线) 有12 个控制点，绿色实线是对应的曲率梳；(d)新的拓扑结构) Fig.13 Boundary fairing and simplification of a Column-shape surface ((a) Column-shape surface.The original boundary shape (red solid line) has 21 control points,and the green solid line is the corresponding curvature comb;(b) Original topology; (c) Boundary shape fairing by the new algorithm.The fairing boundary shape (red solid line) has 12 control points,and the green solid line is the corresponding curvature comb;(d) New topology)

例2 是Mountain-shape 曲面，其是具有121 个控制点的三次B 样条曲面。图14(a)中的红色实线是选择的边界部分，绿色实线是对应的曲率梳。由图14(a)和(c)可知，光顺后的边界曲线比原边界曲线具有更少的曲率单调段。基于新算法，采用7个控制点对原曲面的边界曲线进行了光顺和简化(图14(a)～(d))。由光顺前后的高光图可知，控制点 个数的减少对曲面形状产生了一定的影响，但差异不大。对曲面进行简化时，剔除冗余点越多，结果越偏离原形状，因此需要在保证形状基本不变的前提下，对曲面进行简化。

图14 Mountain-shape 曲面的边界光顺及简化 ((a) Mountain-shape 曲面。原始边界曲线(红色实线)有11个控制点，绿色实线是对应的曲率梳；(b)原始拓扑结构；(c)用本文算法进行边界光顺。光顺边界曲线 (红色实线)有7 个控制点，绿色实线是对应的曲率梳；(d)新的拓扑结构) Fig.14 Boundary fairing and simplification of a Mountain -shape surface ((a) Mountain -shape surface.The original boundary shape (red solid line) has 11 control points,and the green solid line is the corresponding curvature comb; (b) Original topology; (c) Boundary shape fairing by the new algorithm.The fairing boundary shape (red solid line) has 7 control points,and the green solid line is the corresponding curvature comb;(d) New topology)

传统文献[14]和[16-18]方法由于受矩形拓扑结构的限制，无法得到最终的边界数据简化结果。文献[14]采用非均匀B 样条小波对NURBS 曲线曲面进行光顺与简化，在简化后需要重新调整边界控制点，无法局部压缩边界控制点的个数。本文方法则能够对非矩形拓扑结构的曲面边界区域进行光顺，利用T 样条技术进一步得到控制点简化后的模型。

4 结束语

本文提出了一种基于T样条与小波技术的曲面边界光顺及简化算法。首先利用非均匀B 样条小波对边界部分进行分解和光顺。然后基于T-mesh 进行曲面重构，得到具有光顺边界的T 样条曲面。与文献[14]和[16-18]传统方法相比，新算法允许光顺曲面中存在非矩形拓扑结构，因此对曲面边界进行光顺时可以大大简化数据。