某导弹生产定型靶试数量的可靠性分析

李根成 李洪宇

摘 要： 为了确定兼顾考核自主飞行可靠度的生产定型靶场试验所需导弹数量， 首先介绍了使用方推荐的以成熟期目标值为检验下限设计的靶场试验方案， 之后对不同可靠性的导弹通过推荐靶试方案的概率进行了定量分析。 即使可靠性达到了目标值， 导弹通过使用方推荐靶试方案的概率依然很小， 进而指出以目标值作为检验下限设计的靶试方案不正确。 生产定型靶试方案以既能考核可靠性最低可接受值又能对成熟期目标值摸底进行设计， 按此原则确定了生产定型靶场试验所需导弹数量及允许的失败次数。

关键词：可靠性; 生产定型; 靶试; 目标值; 最低可接受值; 检验下限

中图分类号：    TJ760.6    文献标识码：    A   文章编号：1673-5048（2021）04-0007-04

0 引  言

面临传统定型管理“一考定终身”带来的装备交付不顺利、 质量不稳定等问题， 按机关要求， 某改进型导弹需在设计定型后先小批试生产， 在批量生产工艺及质量控制稳定性等问题解决后进行生产定型， 之后再批量生产。 该型导弹按国发[2005]32号文《军工产品定型工作规定》进行生产定型， 即分工艺和生产条件考核、 部队试用、 生产定型试验、 生产定型审查四个阶段实施[1]。

参照设计定型试验， 生产定型试验包括靶场外的功能性能、 环境、 可靠性等鉴定试验和靶场试验[2]。 环境、 可靠性试验各需消耗2枚导弹， 靶场试验消耗导弹多， 且实弹发射时还要损耗目标机， 导弹和目标机都价格不菲， 因此在达到考核要求的前提下应尽量少发射导弹。 使用方与生产方在确定靶试导弹数量时产生了分歧， 即使用方提出， 靶试用导弹数量按不允许失败条件下检验可靠性目标值计算， 而生产方认为， 不能将目标值作为检验下限设计生产定型靶试方案。 本文从可靠性角度对生产定型靶试导弹数量进行分析。

1 原生产定型靶试导弹数量设计

据经典方法， 设计定型时靶场试验除考核战术技术性能外， 还兼顾考核导弹自主飞行可靠度[2-3]。 研制总要求中规定该型导弹自主飞行可靠度： 目标值不小于0.91（置信度0.80）， 最低可接受值不小于0.73（置信度0.70）。

设计定型时产品可靠性不得低于最低可接受值[4-6]， 所以设计定型靶试方案应保证： 通过靶场试验， 评估出置信度0.70时， 自主飞行可靠度置信下限（记为R0.7）不得低于0.73。 本着少消耗导弹又能考核其战术技术性能的原则， 靶试至少要覆盖7条不同弹道。

设计定型时共研制20枚导弹， 使用方与生产方综合权衡后， 确定了（8， 1）的靶试方案， 即抽取8枚导弹进行8条弹道的发射试验， 8枚导弹中允许失败1枚。

由于样本量与批量之比大于0.1， 按GJB376《火工品可靠性评估》中的超几何分布公式对不同靶试结果进行评估[7]：

∑Fx=0n！（N-n）！（N-NR）！（NR）！N！x！（n-x）！（N-NR-x）！（NR-n+x）！=1-γ（1）

式中： n为靶试数量; N为本批导弹数量; F为靶试失败次数; R为自主飞行可靠度; γ为置信度。 以CnN表示从N个产品中随机抽取n个的组合数， 则式（1）可转换为

∑Fx=0CxN-NR×Cn-xNRCnN=1-γ（2）

式中： 左边表示从N枚导弹中随机抽取的n枚中不合格数不超过F的概率， 记为P（R）。 式（2）可解读为可靠度为R的导弹通过方案（n， F）的概率为1-γ[8]。

当8枚导弹全靶试成功时， 按式（1）计算出R0.7=0.885 2; 有1枚靶试失败时， R0.7=0.747 4; 有2枚失败时， R0.7=0.616 4， 小于最低可接受值0.73。 故靶试方案（8， 1）能夠兼顾考核该型导弹自主飞行可靠度。

生产定型靶试用导弹从小批试生产的产品中抽取， 该批产品共生产50枚。 使用方认为， 相对于设计定型靶场试验兼顾考核自主飞行可靠度的最低可接受值， 生产定型靶场试验应考核目标值， 即设计的生产定型靶试方案应能保证： 若靶试成功， 置信度0.80时， 导弹自主飞行可靠度下限应不低于0.91。

将γ=0.80， R≥0.91代入式（1）， 可得： 当F=0时， n≥15; 当F=1时， n≥27。 即为检验自主飞行可靠度是否达到目标值0.91， 不允许失败时， 需要至少15枚导弹; 允许1枚失败时， 需消耗27枚导弹。 考虑到试验消耗及试验周期等因素， 使用方提出生产定型靶场试验采用（15， 0）方案。

航空兵器 2021年第28卷第4期

李根成， 等： 某导弹生产定型靶试数量的可靠性分析

2 原生产定型靶试方案的可靠性分析

无论是设计定型靶试或生产定型靶试， 都是抽样检验， 会犯两类错误： （1）将合格产品误判为不合格产品而加以拒收， 致使生产方受损失， 犯这类错误的概率为生产方风险， 一般用α表示; （2）将不合格产品误判为合格产品而予以接收， 致使使用方受损失， 犯这类错误的概率为使用方风险， 一般用β表示。

理想的抽样检验方案是α=β=0， 但这种方案不存在。 实际工作中通常是生产方和使用方共同协商， 确定两个值R0和R1， 当产品批的实际可靠度R≥R0时， 以大概率接收整批产品， 即要求R≥R0时， P（R）≥1-α; 当R=R0， P（R）=1-α。 当R≤R1时， 以小概率接收整批产品， 即要求R≤R1时， P（R）≤β; 当R=R1， P（R）=β。 标准型一次抽样方案的设计公式如下[3-4]：

P（R0）=1-αP（R1）=β （3）

在使用方和生产方商定了适当的方案参数R0， R1， α， β后， 利用式（1） 和式（3）即可得到检验方案（n， F）。 由于n， F必须是非负整数， 所以式（3）常近似地被满足。 将求得的n， F代入式（3）， 可求得采用该方案时生产方实际承担的风险α′和使用方实际承担的风险β′。

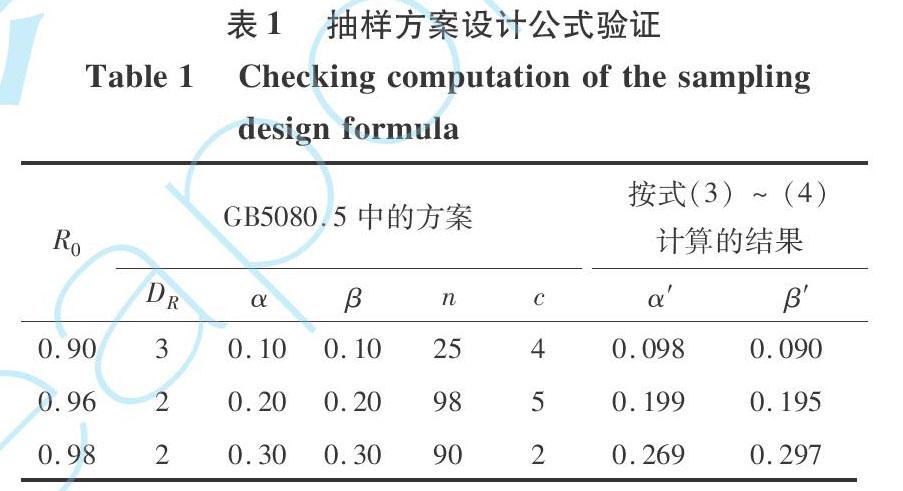
GB5080.5《设备可靠性试验成功率的验证试验方案》中的定数试验方案就是依据式（3）设计的[9]， 只不过GB5080.5是用二项分布式计算的， 而不是式（1）～（2）中的超几何分布[4， 7-8]。  二项分布式是超几何分布公式在n/N<0.1时的简化[7]：

∑Fx=0CxnRn-x（1-R）x=1-γ（4）

实际风险值α′和β′与标称风险值α和β很接近， 如表1所示。 表1中， DR=（1-R1）/（1-R0）为成功率鉴别比[9]。

引言中提到的生产方与使用方之间的分歧， 本质上是对风险认识的不统一。 使用方认为生产定型时应考核目标值， 因此把γ=0.80， R≥0.91代入式（1）计算靶试导弹数量。 按式（1）设计出的方案无论是（15， 0）或是（27， 1）， 其实质都是把0.91当作抽样检验方案中的检验下限， 且使用方风险β=1-γ， 即把成熟期目标值作为检验下限设计方案。 文献[10]以某型导弹为例， 详细论述了不能将目标值作为检验下限设计生产定型可靠性鉴定试验方案， 用最低可接受值、 目标值及介于其间的值， 按式（4）计算不同可靠度的导弹通过靶试方案（15， 0）和（27， 1）的概率， 计算结果见表2。

GJB1909A《装备可靠性维修性保障性要求论证》中定义， 目标值是期望战备达到的使用指标[11]， 即目标值是期望值， 是成熟期可达到的理想值。 按美国对装备的采购激励政策， 装备在成熟期达到目标值时可获得奖金[12]。 而表2显示， 可靠度达到成熟期目标值0.91的导弹通过方案（15， 0）的概率是0.187， 通过方案（27， 1）的概率是0.180。 即虽然导弹可靠性已达到期望值， 但通过方案（15， 0）或（27， 1）的概率都很低， 这显然与得到奖励背道而驰。 导致靶试方案（15， 0）不合理的原因是将成熟期目标值当作检验下限[10]。

3 建议的靶试方案

既然不能将成熟期目标值当作检验下限设计靶试方案， 那么该如何设计。 由第2节的描述可知， 一旦确定了R0， R1， α， β， 由式（1）和式（3）即可得出方案（n， F）， 即方案设计的核心是确定检验下限R1及相应的β、 检验上限R0及相应的α。

生产定型是在试生产后批量生产前进行的， 此时产品可靠性可能随着工艺完善或对部队试用中暴露出问题的改进有适当增长， 但基本与设计定型时水平相当[13-14]。 由第2节的分析可知， 即使该阶段产品可靠性已接近或达到成熟期目标值， 也不能将目标值作为检验下限设计靶试方案， 因为可靠性达到目标值的好产品通过这种靶试方案的概率很低[10]。

生产定型时鉴定可靠性指标的试验应以最低可接受值作为检验下限， 这在一些标准中也有明确规定[15-16]， 如GJB5414《炮射导弹武器系统定型试验规程》适用于设计定型和生产定型试验， 其“17.18.3试验方案”中规定可靠性试验“以战术技术指标规定的平均无故障工作时间的最低要求为θ1”[16]（θ1在GJB5414中为检验下限）。 以最低可接受值对应的置信度确定β， 即β=1-γ， 也就是说产品通过满足P（R1）=β的方案考核时， 能够以置信度γ保证产品可靠性不低于R1， 因产品可靠性为R1时， 通过该方案概率仅为β[4]。

另外， 还要保证好产品大概率通过靶试方案。 可靠性达到目标值的产品应是好产品[12， 17]， 故将目标值作为检验上限， 由其对应的置信度确定α， 即α=1-0.80=0.20， 产品可靠性为R0时， 通过该方案概率為1-α， 通不过的概率为α。 故设计的方案（n， F）应尽量满足：

P（R1）=0.30P（R0）=0.80 （5）

将N=50， R0=0.91， R1=0.73代入式（5）得到几组近似解：

（1） 方案（8， 1）时， P（0.73）≈0.298， P（0.91）≈0.856;

（2） 方案（12， 2）时， P（0.73）≈0.300， P（0.91）≈0.942;

（3） 方案（16， 3）时， P（0.73）≈0.294， P（0.91）≈0.983。

虽然生产定型可靠性试验的检验下限是最低可接受值， 但使用方坚持靶试导弹数量按能对目标值摸底进行设计。 因靶试结果为（15∶0）即发射的15枚导弹全部成功时， 0.80置信度下的可靠度下限为0.913 5; （14∶0）时， 0.80置信度下的可靠度下限为0.906 4， 故靶试数量不应低于15枚。

考虑到生产定型时产品可靠性比设计定型时有适当提高， 故使用方和生产方最终确定的方案是（15， 2）。 将N=50、 n=15、 F=2代入式（1）得P（0.73）≈0.140， P（0.91）≈0.891， 即可靠度为0.73时通过方案（15， 2）的概率是0.140， 可靠度为0.91时通过概率是0.891， 满足“差产品低概率通过、 好产品大概率通过”检验原则。 表3列出了不同试验结果下的可靠度评估值。

由表3知， 试验结果为（15∶2）时， R0.7=0.784 5， 满足最低可接受值不小于0.73（置信度0.70）的要求; （15∶3）时， R0.7=0.713 8， 说明导弹自主飞行可靠度不满足要求; （15∶0）时， R0.8= 0.913 5， 说明15枚的靶试数量能够对目标值进行摸底。

4 结 束 语

生产定型是在试生产后、 批量生产前进行的， 主要检验生产工艺是否满足稳定批量生产的要求， 避免由于工艺和生产条件不完善导致批生产产品的质量下降。 若将成熟期目标值作为检验下限设计生产定型靶试方案， 必然导致可靠性达到要求的导弹通过靶试考核的概率低。

文末给出的生产定型靶试方案（15， 2）， 既能检验导弹可靠性不小于最低可接受值， 且能对是否达到成熟期目标值进行摸底。

参考文献：

[1] [2005]32号 军工产品定型工作规定[Z].

[2005]32 Rules for Finalization of Military Products[Z].（in Chinese）

[2] 樊会涛， 杨晨， 周颐， 等. 空空导弹系统试验和鉴定[M]. 北京： 国防工业出版社， 2007.

Fan Huitao，  Yang Chen， Zhou Yi， et al. Air-to-Air Missile Systems Test and Evaluation [M]. Beijing： National Defense Industry Press，  2007.（in Chinese）

[3] GJB 899A-2009 可靠性鉴定和验收试验[S].

GJB 899A-2009 Reliability Testing for Qualification and Production Acceptance[S]. （in Chinese）

[4] 李根成. 空空导弹可靠性试验技术研究[D]. 北京： 北京航空航天大学， 2007.

Li Gencheng. Research on Air-to-Air Missiles Reliability Test Technology [D]. Beijing： Beijing University of Aeronautics and Astronautics，  2007. （in Chinese）

[5] 王自力. 可靠性維修性保障性要求论证[M]. 北京： 国防工业出版社，  2011.

Wang Zili. Demonstration of Reliability，  Maintainability and Supportability Requirements[M]. Beijing： National Defense Industry Press，  2011.（in Chinese）

[6] 康锐. 可靠性维修性保障性工程基础[M]. 北京： 国防工业出版社，  2012.

Kang Rui. Fundamentals of Reliability & Maintainability & Supportability Engineering[M]. Beijing： National Defense Industry Press，  2012.（in Chinese）

[7] GJB 376-1987 火工品可靠性评估方法[S].

GJB 376-1987 Assessment Method of Reliability of Initiating Devices[S]. （in Chinese）

[8] 李根成，  吴昌. 基于靶试的导弹自主飞行可靠度评估研究[J]. 航天控制，  2018，  36（4）： 94-97.

Li Gencheng，  Wu Chang. Research on Self-Flying Reliability for Missile Using the Firing Test Data[J]. Aerospace Control，  2018，  36（4）： 94-97.（in Chinese）

[9] GB 5080.5-1985 设备可靠性试验成功率的验证试验方案[S].

GB 5080.5-1985 Equipment Reliability Testing： Compliance Test Plans for Success Ratio[S]. （in Chinese）

[10] 李根成. 生产定型可靠性鉴定试验检验下限研究[J]. 航空兵器，  2019，  26（2）： 81-85.

Li Gencheng. Research on Lower Test Value of Reliability Qualification Test for Manufacture Finalization[J]. Aero Weaponry，  2019，  26（2）： 81-85.（in Chinese）

[11] GJB 1909A-2009 装备可靠性维修性保障性要求论证[S].

GJB 1909A-2009  Demonstration of Reliability，  Maintainability and Supportability Requirements for Materiel[S]. （in Chinese）

[12] 任占勇. 试论可靠性统计试验方案中检验上限、 下限与可靠性指标的关系[J]. 航空标准化与质量，  1995（2）： 45-47.

Ren Zhanyong. Relation among Reliability Index， Upper Value and Lower Value in Reliability Verification Test[J]. Aeronautic Stanardization & Quality，  1995（2）： 45-47.（in Chinese）

[13] 龚庆祥. 型号可靠性工程手册[M]. 北京： 国防工业出版社，  2007.

Gong Qingxiang. Reliability Engineering Manual for Materiel [M]. Beijing： National Defense Industry Press，  2007.（in Chinese）

[14] 何国伟. 美国运载火箭的可靠性分析及从中的启示[J]. 质量与可靠性，  1996（1）： 36-39.

He Guowei. Reliability Analyzing of American Launch Vehicle and the Revelation[J]. Quality and Reliability，  1996（1）： 36-39.（in Chinese）

[15] GJB 4396-2002 微光夜视仪定型试验规程[S].

GJB 4396-2002 Approval Test Procedure for Night Vision Instrument of Low-Light[S].（in Chinese）

[16] GJB 5414-2005 炮射导弹武器系统定型试验规程[S].

GJB 5414-2005 Test Procedures for Finalize the Design of Gun-Launched Missile Weapon System[S].（in Chinese）

[17] 何國伟. 关于θ0与θ1的讨论[Z].  质量与可靠性简报， 1997（95）.

He Guowei. Research on θ0 and θ1[Z].  Briefing on Quality & Reliability，  1997 （95）.（in Chinese）

Reliability Analyzing on  Missiles Number Using in

Manufacture Finalization Firing Test

Li Gencheng1*，  Li Hongyu2

（1. China Airborne Missile Academy， Luoyang 471009， China; 2.Unit 93196 of PLA， Urumqi  841700， China）

Abstract：

To determine the missiles number using in the manufacture finalization firing test to examine the missiles self-flying reliability. Firstly，  the firing test scheme recommended by the consumer is introduced，  which is designed under the condition that the maturity goal is taken as the lower test limit，  then quantitatively analyzing the probabilities passing the recommended firing test scheme when the missiles reliability is different. The probability passing the recommended firing test scheme is small even though the missiles reliability is equal to the maturity goal，  the reason is that the maturity goal be wrong taken as the lower test limit. The manufacture finalization firing test scheme should be designed according to the principle which the reliability minimum acceptable value be examined and whether the maturity goal can be reached or not，  so that the missiles number using in the manufacture finalization firing test and the failure number allowed are determined.

Key words： reliability; manufacture finalization; firing test; maturity goal; minimum acceptable value; lower test limit