表面粗糙度预测及三维形貌仿真

宫 欢，聂 娇，李金泉

(沈阳理工大学 机械工程学院，辽宁 沈阳 110159)

金属切削加工是一种常见的加工方式，长期以来，人们对切削加工的特点已进行了广泛研究。Rao等采用陶瓷刀具对AISI1050钢进行车削试验，得到了下列结论：切削深度对表面粗糙度的影响十分显著；进给量对表面粗糙度也有一定的影响[1]。张蕊在研究切削参数对切削力的影响时发现，当切削力增大时，工件的表面粗糙度显著增大,且会降低其表面质量[2]。张斌通过回归分析，用响应曲面法建立了表面粗糙度预测模型[3]。该模型预测精度高，能用于预测加工参数对加工表面粗糙度的影响，有助于了解已加工表面质量随加工参数的变化规律，为切削参数的优选和表面质量的控制提供依据，且为三维形貌仿真奠定了理论基础。

本文主要针对铜合金的切削加工,将理论分析与试验相结合，在不同切削用量下进行表面粗糙度的预测，并对加工表面的三维形貌进行仿真。

1 切削试验与结果

采用CGK6125型数控车床，对半径为100 mm的QAL9-4铝青铜(以下简称铜合金)进行外圆柱面的切削试验。整个加工过程为干式切削。试验用刀具为YG6硬质合金刀片。

切削后采用TR100型电动粗糙度测量仪采集粗糙度数据。铜合金切削试验的因素和水平如表1所示。铜合金切削加工的表面粗糙度试验结果如表2 所示。

表1 铜合金切削试验的因素和水平

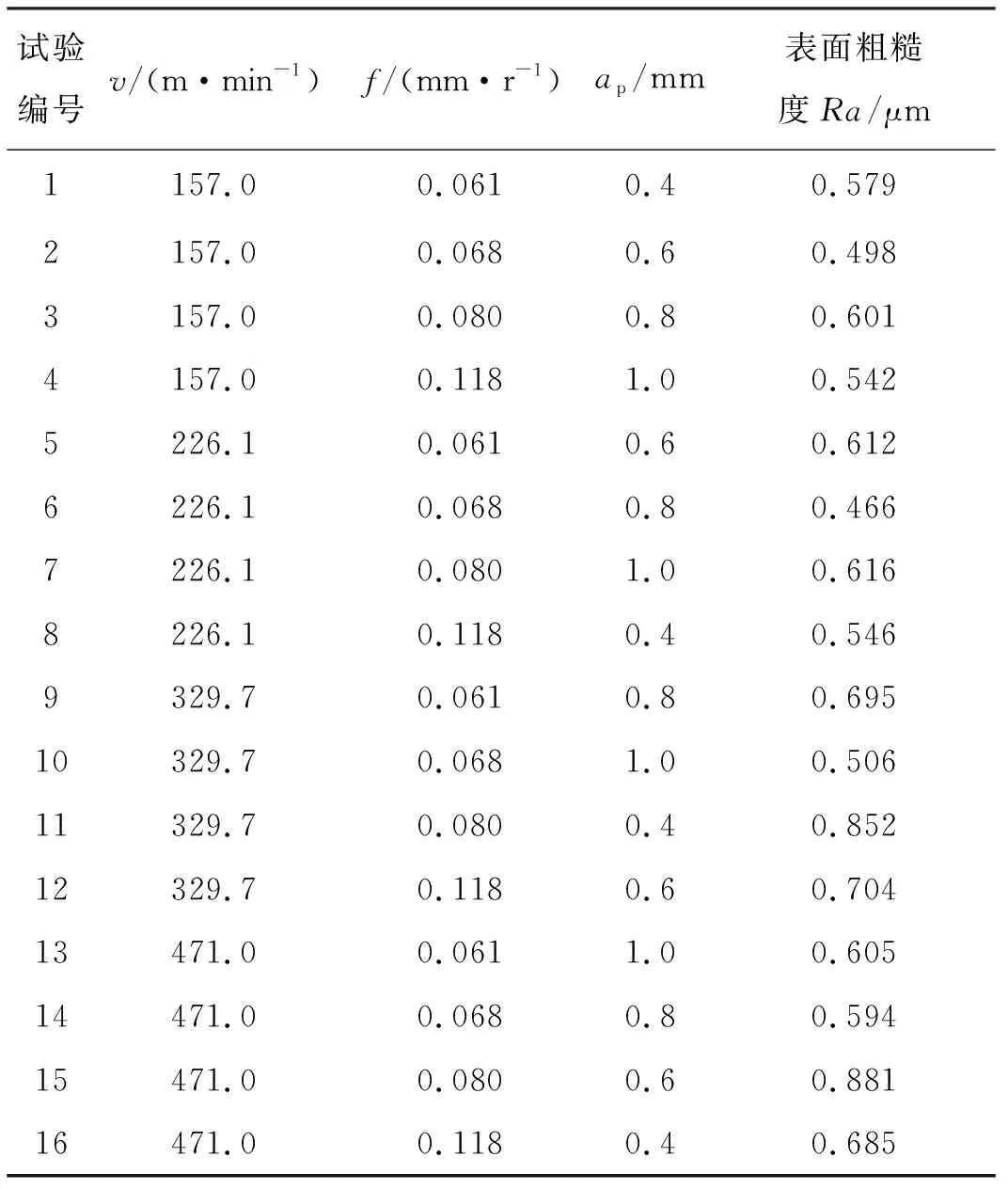
表2 铜合金切削加工的表面粗糙度试验结果

2 结果分析与讨论

2.1 进给量和背吃刀量对粗糙度的影响

根据表2试验编号1-4的数据，在固定切削速度157.0 m/min下,将进给量和背吃刀量增大，可划出图1所示的表面粗糙度变化折线。

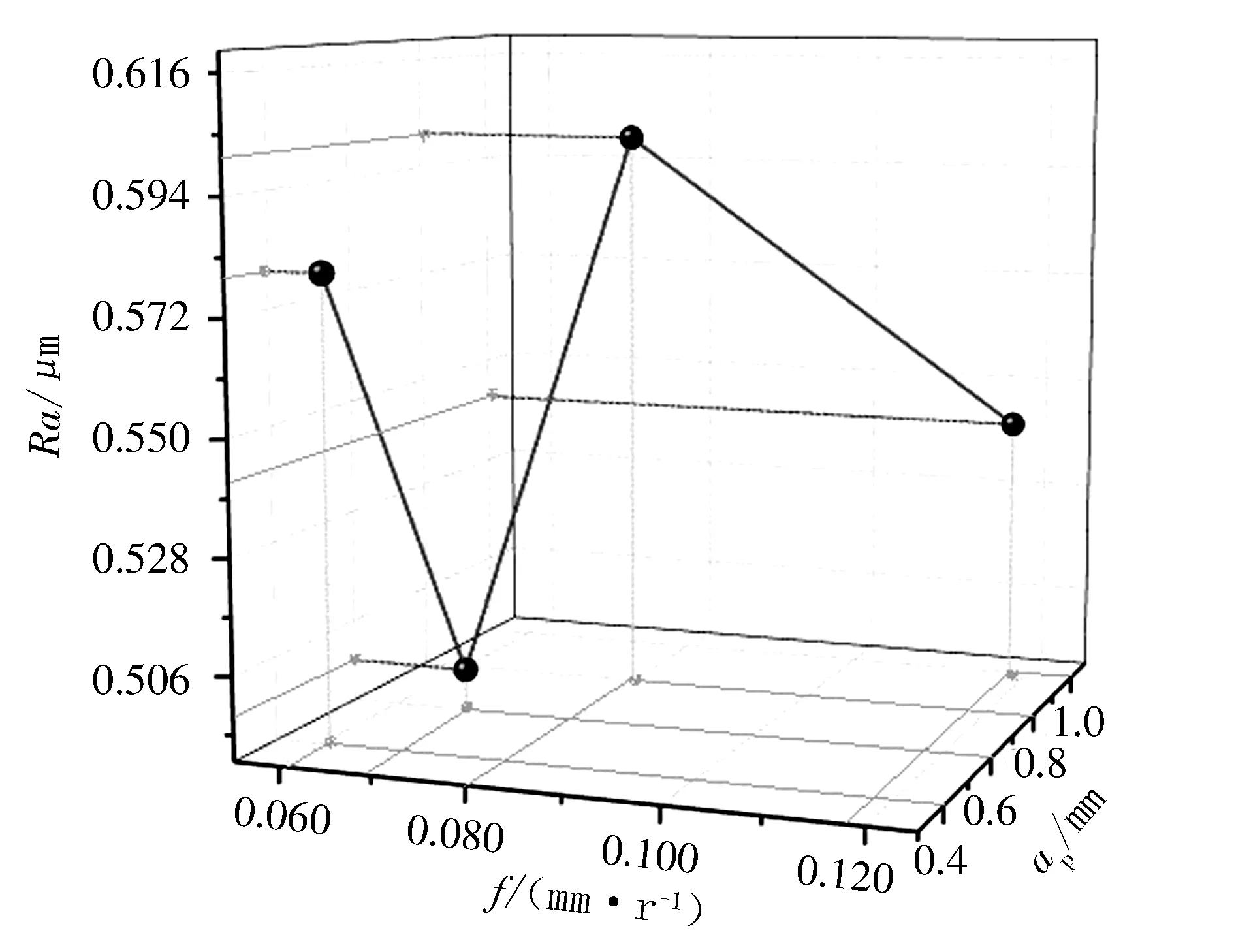
图1 切削速度不变时进给量和背吃刀量对粗糙度的影响

由图1可看出，随着进给量和背吃刀量的逐渐增大，表面粗糙度会发生变化，当进给量为0.068 mm/r、背吃刀量为0.6 mm时，表面粗糙度最小。

2.2 切削速度和背吃刀量对粗糙度的影响

根据表2试验编号1、5、9、13的数据，在固定进给量0.061 mm/r下,将切削速度和背吃刀量增大，可划出图2所示的表面粗糙度变化折线。

图2 进给量不变时切削速度和背吃刀量对粗糙度的影响

由图2可看出，随着切削速度和背吃刀量的逐渐增大，表面粗糙度先增大后减小，表面粗糙度的峰值出现在切削速度为329.7 m/min、背吃刀量为0.8 mm 之时。

2.3 切削速度和进给量对粗糙度的影响

根据表2试验编号1、8、11、16的数据，在固定背吃刀量0.4 mm下，将切削速度和进给量增大，可划出图3所示的表面粗糙度变化折线。

图3 背吃刀量不变时切削速度和进给量对粗糙度的影响

由图3可看出：随着切削速度的增大，表面粗糙度会发生变化，其峰值同样出现在切削速度为329.7 m/min 之时；但相应的进给量为0.080 mm/r，与图2相比进给量较大，表面粗糙度的值也较大。因此，加工过程中要尽可能控制切削速度和进给量，以免表面粗糙度过大。

3 表面粗糙度预测

若在工件加工时测量表面粗糙度，则会降低加工效率，增大成本。为此，可采用适当的粗糙度理论模型来预测表面粗糙度，并对加工表面的三维形貌进行仿真。为了定量分析切削速度v、进给量f、背吃刀量ap对表面粗糙度Ra的影响，文献[4]采用线性回归方法得出了下列关系式：

(1)

式(1)即本文进行表面粗糙度预测的原始模型。对该式进行处理，在等号两边取对数，得到的线性函数为：

lgRa=lgC+klgv+mlgap+llgf

(2)

应用Matlab软件，根据式(2)拟合表2试验数据，可得：C=e-1.167，k=0.2 254，m=-1.119 7，l=0.251 4。将这几个系数代入式(1)，可得表面粗糙度的最终预测模型，即

Ra=e-1.167v0.225 4ap-1.119 7f0.251 4

(3)

根据式(3)，应用Matlab软件编写表面粗糙度计算程序，用于验证表2中试验编号2对应的数据。在图4 所示的表面粗糙度计算界面填入数据，进行计算。计算粗糙度(结果)为0.530 46，与表2中相应试验结果接近。因此可判定，表面粗糙度的最终预测模型(式(3))能够与试验结果较好吻合。

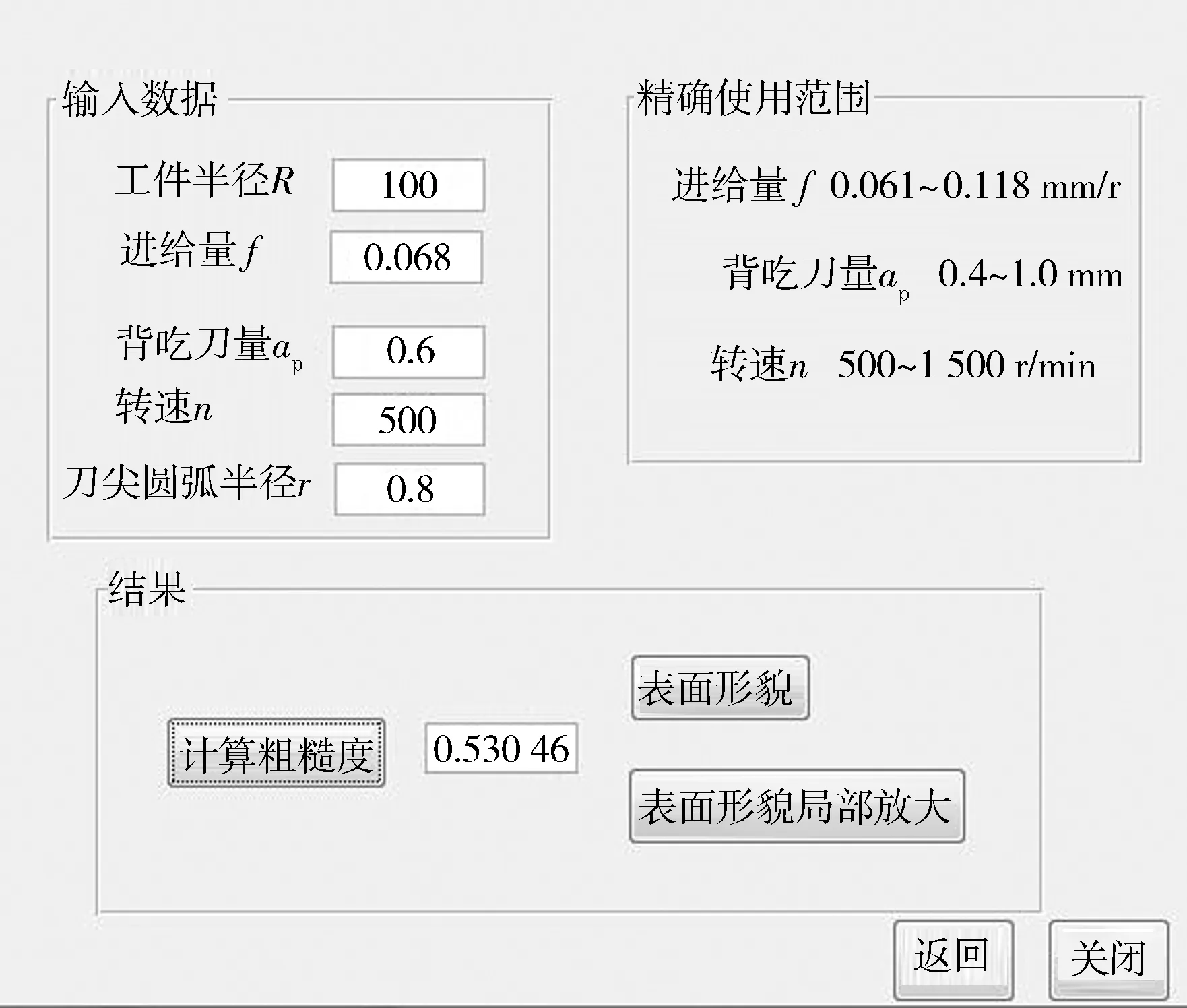
图4 表面粗糙度计算界面

4 表面三维形貌仿真

表面粗糙度Ra，为一维变量，无法反映工件表面三维形貌的特征。工件在切削时，由工件的旋转形成主切削运动，刀具的运动为进给运动，工件为回转体。工件和刀具因相对运动而产生摩擦和振动，会造成工件表面材料的塑性变形。随着刀具相对工件的螺旋进给运动，刀具几何形状的变化会导致在工件轮廓上残留形状、尺寸各不相同的谷和峰(即表面三维形貌)。因此，可根据理论正弦振动和刀尖的成形运动，按刀具的轨迹坐标进行仿真[5]。本文将参考文献[6]，以刀具几何形状的轨迹点和正弦振动作为模型进行表面三维形貌仿真。该模型也用于计算车削时工件表面的残留面积，即：

(4)

式中：k为截面个数(q=0，1，2，…，Np)，Np为截面总数；j为轨迹点个数(j=0，1，2，…，Nt)，Nt为轨迹点的总数；i=0,1,2，…,N(其中，N=Nt/Np);振幅A=0.001 5 mm；频率fr=20 Hz；变量H=120πfr/Np；φ为相位偏移；r为刀尖圆弧半径，r=0.8 mm。

针对P点，可将式(4)应用于Matlab软件，结合表面粗糙度拟合公式,对工件已加工表面的三维形貌进行仿真。表面粗糙度越大，其三维形貌的变化越明显。

在三维形貌仿真时，一定要注意数据的合理性[7]。在进给量f小于等于刀尖圆弧半径的75%时，背吃刀量ap过小会无法形成切屑，过大则无法加工[8]。本文采用Matlab软件和表2中第1-4组试验数据进行仿真。仿真所得工件表面三维形貌如图5所示。其中，转速n=500 r/min，对应的切削速度v=157.0 m/min。

从图5可看出，当进给量和背吃刀量逐渐增大时，铜合金的表面形貌也逐渐变化，其表面形貌宏观波纹的波动程度逐渐变大。仿真结果与试验数据对比有一定的误差，但总体上较为接近。研究认为，三维形貌仿真形象直观，可替代部分试验。

(a) f=0.061 mm/r, ap=0.4 mm

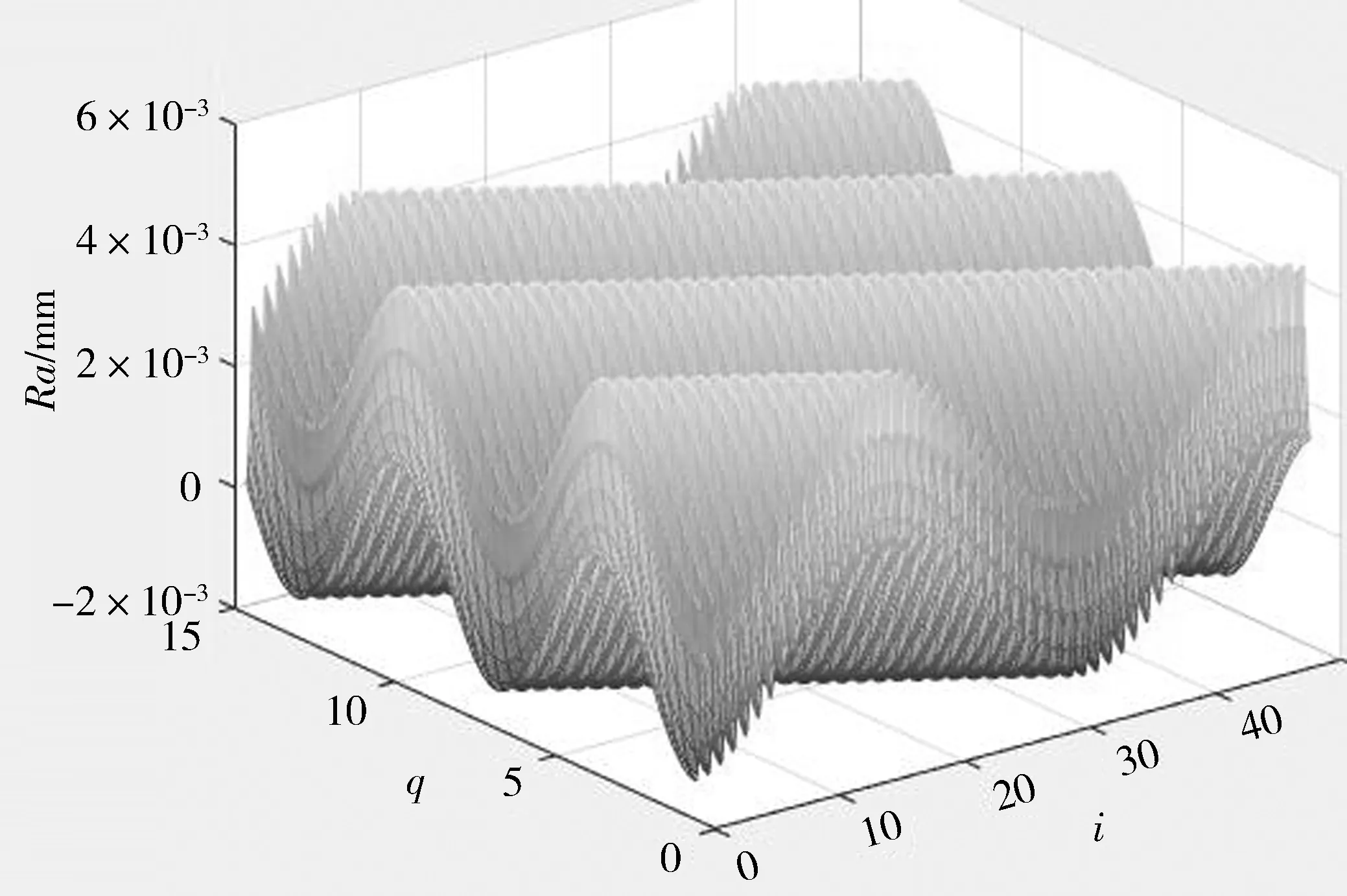
(b) f=0.068 mm/r, ap=0.6 mm

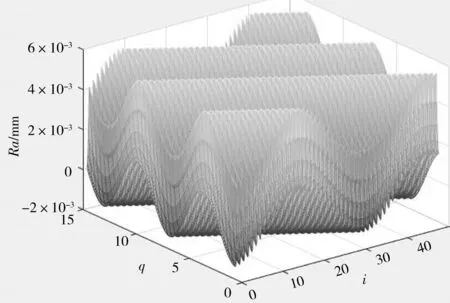
(c) f=0.080 1 mm/r, ap=0.8 mm

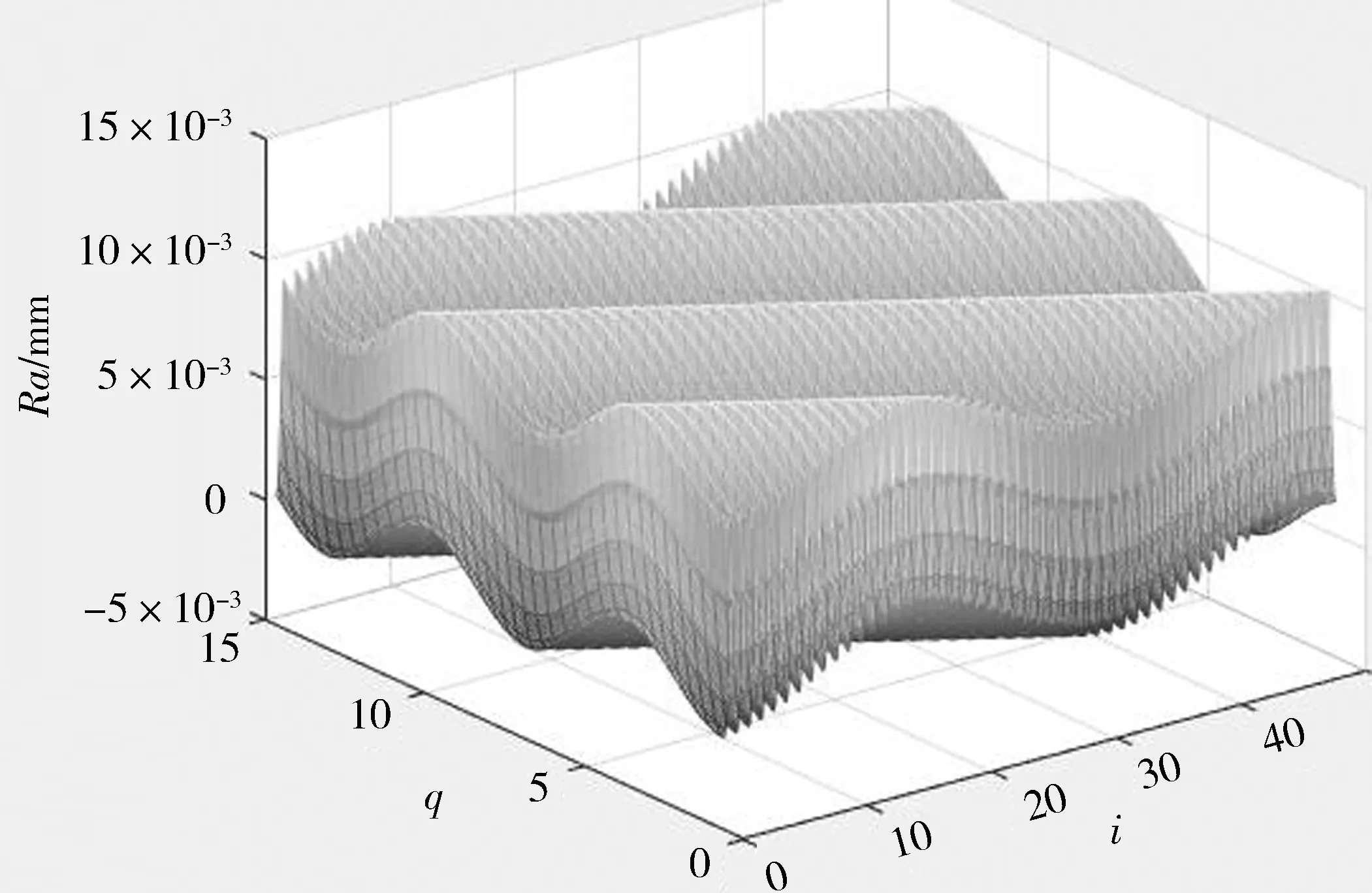
(d) f=0.118 mm/r, ap=1.0 mm图5 工件表面三维形貌

5 结 论

(1) 在干式切削条件下，表面粗糙度预测模型为：Ra=e-1.167v0.225 4ap-1.119 7f0.251 4。其预测值能够与试验结果较好吻合。

(2) 加工表面三维形貌仿真的结果与试验结果总体上较为接近。