基于磁梯度法的地下深埋管线探测方法研究
吴楚怡,安 聪
[地泰克工程勘察(上海)有限公司,上海市 201206]
0 引言
随着工程建设项目规模的日渐扩大和非开挖施工工艺铺设地下管线技术的发展,地下管线越埋越深。在地铁建设或市政顶管等地下工程经过这些开挖困难的区域时,既要避开浅层地下管线,又要绕开已有的地下构筑物,并保持一段安全的施工距离。这种复杂的埋置条件下,常规物探方法很难满足实际探测工作的需要,急需将更先进的地球物理方法应用于地下管线探测中。
目前,被广泛应用于非开挖深埋管线的物探方法有信标示踪法、陀螺仪法、主动磁源法和井中磁梯度法等。其中,井中磁梯度法在一些重大工程建设项目中开始应用并得到了较好的反馈。一部分国内外学者将井中磁梯度法应用于工程勘察方面,都取得了很好的效果。该方法能够更高效、更准确地探测地下深埋管线,且其梯度测量的特点使其比原来的磁测方法有更高的精度,因而在复杂的管线探测领域有着广阔的应用前景和待挖掘的探测潜力。实际上,井中磁梯度法是目前探测上水、燃气类大埋深非开挖金属管线最有效的方法。但井中磁梯度法仅仅依靠分析磁梯度数据的曲线变化情况和峰值位置来判定目标体的位置和深度,缺少定量的数据分析和计算。
本文在调研、总结地下深埋管线探测主要的探测难点的基础上,通过数值模拟,研究井中磁梯度法探测地下管线的响应特征和规律。另外,通过实测资料反演管线的位置和管径等参数,以验证井中磁梯度法探测地下深埋金属管线的可行性。
1 磁梯度探测方法技术
1.1 管线的磁场
在工程物探中,可把局部区域内的水平管线视为一个无限长的水平圆柱体[1]。
首先讨论地面磁测的情况。在三维空间内,设管线的走向与地面直角坐标系的y 轴平行,布置测线方向与x 轴平行,垂直向下为z 轴。管线的管中心深度设为x0,即管线模型的圆柱体中心位置的z 轴坐标为z0,管线所在位置在测线方向上与坐标原点的距离为y0,则管线中心位置的坐标可表示为(x0,z0)。
由位场理论可知,均匀磁化且密度均匀的物体满足泊松公式,即其磁位可以表达为:

式中:σ 为密度差;G 为万有引力常数;M 为磁化强度矢量;V 为引力位。
由位场理论可知,其在测点(x,z)处的引力位为:

式中:S 为水平圆柱体的横截面积;r 为测点与圆柱体中心位置之间的欧式距离。
设水平圆柱体的有效磁化强度为Ms,其在x 轴、z 轴的分量分别为Mx、Mz。有效磁化倾角为is,则:

设水平圆柱体的直径为d,即水平非开挖金属管线的直径为d,则:

可求得管线的磁场垂直分量ZA和水平分量HA表达式分别为:

式中:μ0为真空磁导率,其值

将式(3)、式(4)、式(5)带入式(6)、式(7)可得:

1.2 管线的井中磁场
在对深埋非开挖管线的探测中,由于常规的自地面进行磁异常测量的电磁感应法已不再得到明显响应。人们想到将磁力探测仪置入钻孔中,由上而下地观测水平金属管线在垂直方向上的ZA曲线变化,即井中磁测[2]。
在地面探测中进行磁力探测时,设置的测线方向为水平方向;在井中探测时,设置的测线方向是垂直方向,其与地面磁测测线垂直。因此,地面磁测的坐标系和井中磁测的坐标系不是同一个坐标系,而是存在一个90°的旋转关系,即地面磁测的坐标系沿y 轴旋转90°可得到井中磁测的坐标系[3]。
设井中磁测的坐标系的横坐标为xH,纵坐标为zH。井中磁测中,有效磁化强度在x 轴、z 轴的分量分别为MxH、MzH。则根据井中磁测坐标系和地面磁测坐标系的关系,可知井中磁测的井中磁测与地面磁测的坐标和磁化强度矢量存在以下关系:

将式(8)~式(13)代入式(6)和式(7),可得井中磁测坐标系下的磁场垂直分量和水平分量分别存在以下关系式:

采用井中磁梯度探测深埋管线考虑的是磁场垂直分量的磁梯度值[4],即应取垂直分量沿垂直方向的导数,即:

2 管线参数的估算方法
利用同一条测线上不同钻孔的井中磁梯度曲线的磁梯度异常和极值异常,可以推断出水平金属管线大致的水平位置和管中心埋深,但无法对目标管线的走向、水平位置和埋深等重要参数进行定量分析[5]。这里通过构造与各欲求参数存在较简单的函数关系的新函数,将复杂的非线性问题转化为简单的线性问题[6]。在确定估算方程的具体形式时,采用最小二乘法进行曲线拟合,得到了估算方程的系数[7]。
2.1 管线参数的估算
2.1.1 有效磁化倾角的估算
由于磁梯度值的极值大小与管线的有效磁化倾角有关,设磁梯度值的极小值与极大值的比值的绝对值为K,即K 满足

根据磁梯度值公式可以模拟得到K 与is的关系图,如图1 所示。
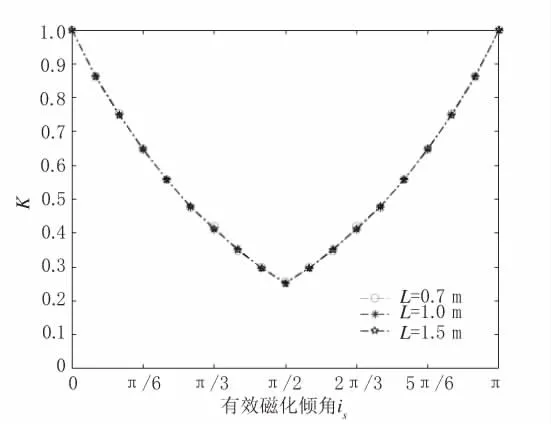
图1 钻孔与管线的水平距离L=0.5 m、1.0 m 和1.5 m时的K-is 曲线
由图1 可知,K 与is之间存在分段关系,其分段点在时取得。对K-is模拟曲线进行分段拟合,可得到K 与is满足以下关系:

利用式(18)即可根据井中磁梯度曲线估算有效磁化倾角的值。
2.1.2 金属管线水平位置的估算
设井中磁梯度曲线出现极大值和极小值的坐标为(Xm1,Zmax)和(Xm2,Zmin),N 为曲线极大值和极小值对应的深度差值,即N 满足:

设N'=N/L 可模拟得到N’-sinis曲线,如图2 所示。
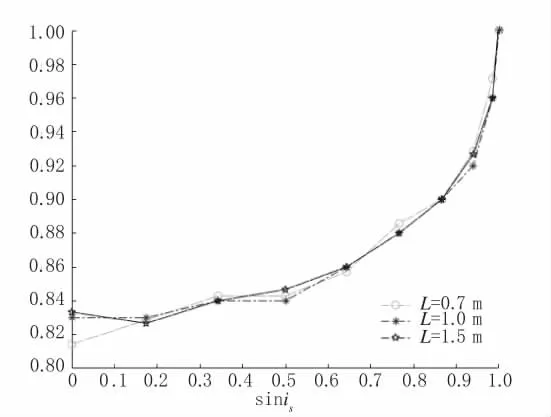
图2 钻孔与管线的水平距离L=0.7 m、1.0 m 和1.5 m时的N’- s inis 曲线
对图2 所示的模拟结果进行曲线拟合,可得N’与sinis的关系如下:

联立式(18)和式(20),即可估算金属管线距离钻孔的水平距离,继而确定金属管线的水平位置。
2.1.3 金属管线埋深的估算
管线的埋深对应磁梯度曲线的极大值和极小值所对应的深度之间,且靠近极值的绝对值更大的那一段。设zm为磁梯度极值的绝对值较大值所对应的深度,可模拟得到S=2|zm-z0|/N 与is的关系图,如图3 所示。
由图3 可知,S 与is之间存在分段关系,其分段点在is=π/2 时取得。对S-is模拟曲线进行分段拟合,可得到K 与is满足以下关系:

图3 钻孔与管线的水平距离L=0.7 m、1.0 m 和1.5 m时的S-is 曲线

联立式(21)和式(20),即可估算金属管线的管中心埋深。
2.2 小结
通过构造与目标参数存在较简单的函数关系的新函数,通过正演模拟数据,采用最小二乘法拟合出新函数与管线参数存在的线性关系式,得到以下公式:

通过上述公式,得到井中磁梯度探测曲线的极值及其对应坐标,即可估算出目标管线的有效磁化倾角、与钻孔的水平距离和管线埋深。
3 工程实例
3.1 工程概况
某工程项目将对温州某区域污水进行牵引,需探明2 处拟建污水顶管施工影响范围内,甲方指定的2 根燃气管道在拟建顶管线路处的水平位置和标高。据资料显示,2 路燃气管线的管径分别为ϕ508和ϕ610。
3.2 数据采集
采用井中磁梯度法探测2 处物探范围内的目标燃气管线,在2 个探测区域分别各布置1 条测线,每条测线对应设置了2 个断面,每个断面上设置5 个钻孔。为避免在钻孔过程中损坏管道的防腐层,按照如图4 所示的顺序进行钻孔探测[8]。钻孔的平面位置如图5 所示。
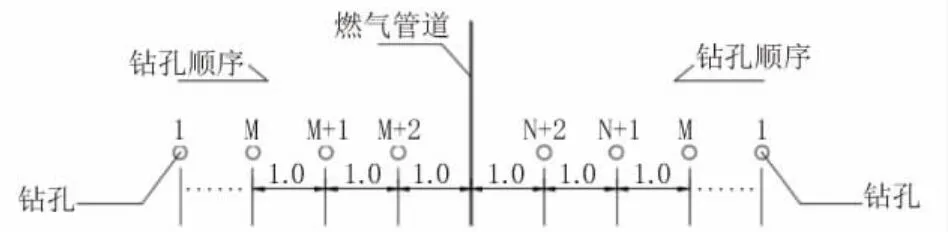
图4 钻孔顺序示意图(单位:m)

图5 两处测线的钻孔布置示意图
3.3 成果分析与解释
对采集的数据进行成图处理。成图时,将磁梯度数据等比例缩放到±10 nT/m 的范围内[9],得到了如图6、图7 所示的井中磁梯度探测成果图。

图6 测线1(断面1、断面2)井中磁梯度探测成果图

图7 测线2(断面3、断面4)井中磁梯度探测成果图
由图6 可以看出,K5 和K6 孔在标高-3.40 m处有明显的磁异常反应且为极值反应;K3、K4、K5和K6 孔在标高-8.80 m 处有明显的磁异常反应,且K4、K5 孔位处出现极值反应。结合此磁梯度探测成果图和搜集资料可以判断,在该断面处,管径为ϕ508 的燃气管在K5、K6 孔之间,管中心标高约为-3.40 m;管径为ϕ610 的燃气管在K4、K5 孔之间,管中心标高约为-8.80 m。比对现场情况,可知K4、K8、K10 深度较浅处出现的磁梯度异常是由钻位附近存在的地表引起的。
由图7 中的磁梯度曲线可以看出,K11 和K12孔在标高-6.30 m 处有明显的磁异常反应且为极值反应;K18 和K20 孔在标高-7.20 m 处有明显的磁异常反应,且K19 孔在冲孔未达指定深度时触及障碍,此时的孔底标高约为-2.50 m。结合此磁梯度探测成果图和搜集资料可以判断,在该断面处,管径为ϕ508 的燃气管位于K19 孔位下方,管中心标高约为-7.20 m;管径为ϕ610 的燃气管在K11、K12 孔之间,管中心标高约为-6.30 m 。比对现场情况,在标高3.00~5.00 m 处产生的磁梯度值异常是由过测线的3 条埋深较浅的管线引起的。
经过资料汇总,本次物探工作共完成磁测断面4个(2 条测线),共20 个测孔。利用磁梯度曲线的极值判断得到目标燃气管的成果,见表1。
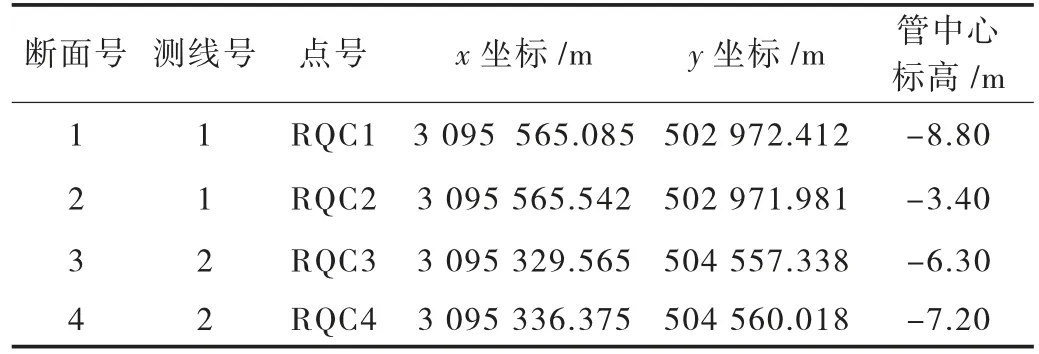
表1 指定点燃气管道磁测成果
为了提高管线探测的精度,现对管线参数进行估算。
对测线1 来说,由图6 可知,K4~K7 孔的磁梯度值变化较明显,故读取实测磁梯度值数据时选择了这4 个孔的数据。得到估算结果见表2、表3。
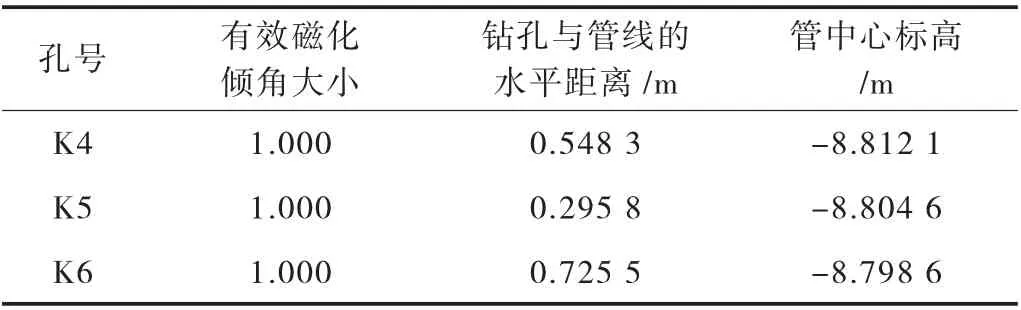
表2 点RQC1 燃气管参数估算成果

表3 点RQC2 燃气管参数估算成果
根据孔位位置的坐标及其相对位置,可进一步求得两点对应的平面坐标及其点位中误差和点深中误差,见表4、表5。

表4 点RQC1 燃气管参数估算成果
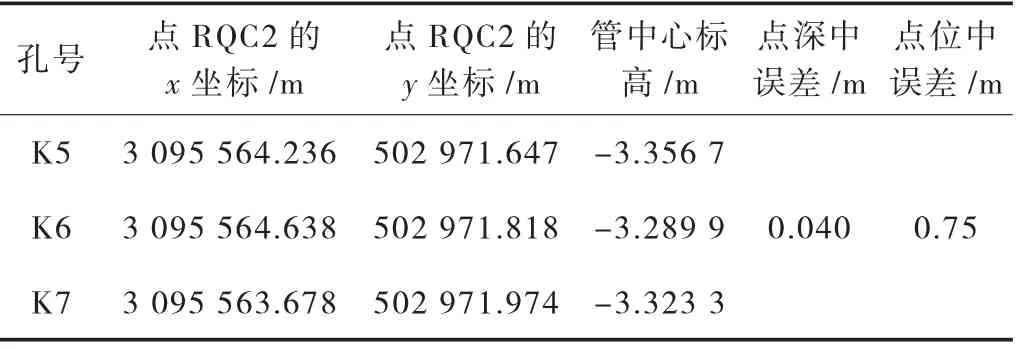
表5 点RQC2 燃气管参数估算成果
孔位得到的对应管线的平均位置和标高取平均值,得到参数估算的最终成果见表6。
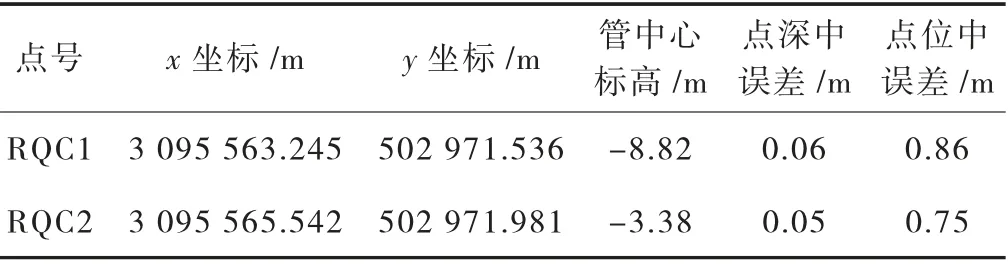
表6 指定点燃气管参数估算成果
对测线2 来说,K11~K13、K17~K19 孔磁异常值的变化比较明显。然而K19 孔触及管线对应的磁梯度曲线并不完整。故读取实测磁梯度值数据时选择了K11~K13、K17~K18 这5 个孔的数据,得到参数估算的最终成果见表7。

表7 指定点燃气管参数估算成果
根据以上2 条测线的管线估测结果可知,估算得到的结果精度要求满足井中磁梯度精测的要求。利用估算得到的管线埋深误差较小,而水平位置估算的误差较大。当考虑管线的尺寸因素后,管线估算的水平误差变小。可知,利用本文设计的管线估算公式得到的管线水平位置还受到管线的尺寸的影响,两者间的关系需要进一步研究确定。
4 结语
本文研究实现了地下深埋管线模型的井中磁梯度正演计算和曲线拟合,从无限长水平圆柱体的磁场强度入手,通过坐标系的转换,推导出地面磁测和井中磁测的磁场水平分量、垂直分量的关系,进一步推导出水平金属管线的井中磁梯度公式。通过对模型正演数据的拟合确定了有效磁化倾角、钻孔与管线的水平距离、管线埋深与模拟的磁梯度值及其对应深度的关系式,并用此关系式进行管线水平位置和埋深的估算。在工程实例中运用估算公式,得到了满足精度要求的结果,证明了估算公式的可能性。
考虑到现实情况的复杂性和模型的多样性,还有以下部分工作尚待继续探究:
(1)本文设计的管线参数估算公式得到的管线埋深误差较小,而水平位置估算的误差较大。当考虑管线的尺寸因素后,管线估算的水平误差变小。可知利用本文设计的管线估算公式得到的管线水平位置还受到管线的尺寸的影响,两者间的关系需要进一步研究确定。
(2)实际探测中,除了管线产生的磁异常,还存在其他干扰。应进一步尝试减少干扰的方法,提高井中磁梯度探测的精度和质量。

