沁润数学文化 明晰数学概念

◎刘丽丽 (厦门市金尚中学，福建 厦门 361009)

数学概念是推导数学定理、法则的逻辑基础，也是学生的认知基础，因此概念教学在初中数学教学中占有重要地位.通过概念教学不仅能让学生掌握概念并应用其解题，还可以培养学生在具体情境中抽象出数学概念的思维方法，养成透过现象看本质的习惯，并使学生拥有将复杂问题简单化的能力.但在应试教育的大环境下，中考很少以某个数学概念为考点来考查学生对这个概念的理解，而是将其固化成几种典型题，因此很多教师根据多年应对中考的教学经验，在教学过程中不注重概念的形成过程，而是直接将概念呈现给学生，并列举概念的理解误区，再通过大量的习题来强化概念.致使学生在不知概念的前因后果的情况下被动接受，多是以死记硬背的方式来记忆概念，这不仅导致学生对概念“只知其然，而不知其所以然”，也不利于学生理解概念本质.当学生遇到现实问题时，这一弊端便显现出来，学生想不到或无法利用所学的数学知识来解决实际问题.因此教师在概念课教学时应从不同的角度帮助学生全方位多层次地理解数学概念，学习有源头背景又有应用流向的数学概念，旨在学生数学素养的提升，这才是数学概念教学的终极目标.而在数学概念教学中渗透数学文化，把数学中抽象的逻辑链条复原为知识生成时的思考过程，提升概念课的文化内涵，把数学概念“有血有肉”地表现出来，进而激发学生积极思考，让学生从文化层面感受数学的鲜活与数学之美，学有温度的数学概念.这不仅有利于学生理解概念本质，同时也能激发学生学习数学的热情.让学生在潜移默化中养成透过现象看本质的习惯，从而提高解决实际问题的能力.

新课标中指出，在数学教学中要关注学生的情感，以学生为中心，通过数学知识的教学发展学生的理性思维.通过对新课标的解读分析，在概念教学中，数学概念生成与辨析、数学概念的应用等方面都可以融入数学文化内容.本文将结合初中教学中两个具体的数学概念，尝试在教学中融入数学文化，从数学课堂概念教学出发，以期帮助学生理解概念本质.

一、融入背景起源促概念生成

数学概念源起何处，流向何方？数学史恰是研究数学概念形成背景的重要途径.学生通过了解数学概念的历史发展过程，梳理前人攻坚克难、排除万难的经历，在数学文化中感受数学概念的历史传承，从而明晰数学概念的本质，并从中获得突破当前问题情境的启示.

例1人教版七年级下§6.3《实数》一节中的无理数概念.

无理数概念对于七年级学生是一个较抽象的数学概念，在它之前已经介绍了有理数的概念，在它之后将学习实数概念.多数学生只是单纯机械记忆而不能从本质上理解无理数的概念，这就导致他们对有理数、无理数、实数这三个抽象的数学概念混淆不清.尝试在无理数概念教学中融入无理数产生及发展的相关史实，让学生了解“无理数”的由来，从本质上理解无理数概念.笔者在教学时是这样向学生介绍无理数概念的：

在学习这节课的前一天向学生布置预习作业：搜集并整理无理数的相关数学史.

师：同学们，你们昨天都搜集了有关无理数的数学史料，哪位同学愿意分享一下无理数是如何被人们发现的？

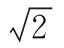
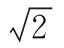
生2：在我国古代，人们很早就发现了无理数，而且有了对实数的系统认识.我国古代就有乘方运算，因此不可避免地就会遇到它的逆运算——开方运算，也就不可避免地遇到无理数.对于这种“开之不尽”，又不能用分数表示的数，我国古代数学家刘徽在《九章算术》中注释“求其微数”，即用十进制小数无限逼近无理数.

师：看来无理数也吸引了我国古代人的兴趣.同学们，你们知道无理数这个名字的由来吗？它真的是没有道理的数吗？

生3：无理数不是没有道理的数.它名字的得来要从明朝的一个科学家徐光启说起，他在翻译《几何原本》时，没有现成的、可对照的词，许多译名都是从无到有创造出来的.徐光启将“ratio(比)”译成了“理”，即“理”就是比的意思.所以“有理数”应理解为“可以写成两个整数之比的数”而不是我们字面上理解的“有道理的数”.因此，曾有人建议，为便于大家理解，把“有理数”和“无理数”改称为“比数”和“非比数”.

通过让学生课前搜集无理数的相关史料，老师与学生在课堂上回顾再现无理数概念的产生、发展的原始情境，这可以更自然地展示无理数概念形成与发展的过程，实现了让学生在知识的发生与发展中理解概念，再通过了解“无理数”名字的由来，让学生明晰概念的本质，就不难将它与有理数、实数的概念区分清楚，进而也能在文化的熏陶中受到思维的启发，提高学生对抽象数学概念的学习兴趣.数学概念的形成背景和过程记录着概念的形成、发展背后的思维过程，在课堂中融入数学史料，让学生身临其境于概念的产生和发展中，深受前人锲而不舍、不断进取精神的震撼，这也将激励学生的学习品质.

二、融入数学文化促概念应用

数学概念的应用是加深学生理解概念的重要途径.学生在应用概念解题时不仅能帮助其理解概念的本质，而且能发展其解决实际问题的能力.在教学中设置有文化背景的应用问题，能加深学生理解概念的同时，让学生感受数学之美，受到文化的熏陶.

例2人教版九年级下§27.1《图形的相似》一节中的相似多边形概念.

相似多边形是继相似图形概念后以描述图形特征的方式给出的概念.学生往往受相似图形概念的影响直接将其理解为形状相同的两个多边形，而不能从“角分别相等，边成比例”的方向去理解，这会使学生在应用概念解决问题时无从下手，找不到解题方向.因此应用概念解决问题是加深学生理解概念的重要途径.课堂中融入有数学文化的问题情境，让学生在应用中不仅能从本质上理解概念，同时感受生活中的数学之美.在课堂中可让学生动手操作：

师：同桌两人一组，拿出课前发的矩形纸，将这张纸沿较长边的中点对折，猜一猜你得到的两个矩形纸片和原来的矩形纸相似吗？

(学生们动手折叠纸片，并观察对比，很快就有几组同学举起了手.)

生：折叠前后的两个矩形纸片形状看上去是相同的，应该是相似的.

师：你们的直观感觉很好，如何验证你的猜想是正确的？

(学生们七嘴八舌地开始讨论，很快就有同学提出了自己的想法.)

生：可以用相似多边形的概念去验证.矩形的角都是直角，已经满足了“角分别相等”的条件，只要它们的边成比例就可以了.

师：你打算如何检验它们的边是否成比例呢？

生：我们组准备用刻度尺测量出两个矩形的长与宽，再计算比较.

师：真是个不错的主意！我们一起动手测量一下吧！

(学生们都积极投入到测量中，陆陆续续传来了他们的测量结果.)

生：原矩形的长是297 mm,宽是210 mm,折叠后的矩形的长是210 mm,宽是148 mm.我们组计算了它们长的比和宽的比大约都是1.4，得出它们是相似的.

师：你们的动手能力很强，这么短的时间里就准确测量并计算得出了正确的结论！接下来请同学们将这张纸如此再对折一次，得到的矩形都相似吗？

(有了上一次的操作经验，这次折叠和验证很顺利，同学们很快就得出二次对折后的矩形和原矩形仍然是相似的.)

师：事实上，有兴趣的同学可以如此继续对折，我们得到的这些矩形都是相似的.这真的是一张奇妙的纸！请同学们仔细看看我们手中的这张纸，你熟悉吗？

生：这就是我们打印时最常用的A4纸.

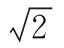
数学概念的理解与掌握，目的是学以致用，解决问题.以A4纸中蕴藏的数学文化为背景，让学生在浓厚数学文化气息中将本节课所学习的相似多边形概念应用到实际问题中，潜移默化地发展了学生审美意识，使学生牢固掌握数学概念的同时体会数学的文化价值.

数学文化融入课堂教学多是介绍数学史，通过历史故事的趣味性增加学生的学习兴趣，本文中除了数学文化对学生情感、态度的培养作用，更重要的是在数学文化的意境中让学生学习有血有肉的数学概念，让学生从根源及本质上理解数学概念、应用数学概念的同时培养数学思维，教会学生思考，进而提升数学素养.数学文化融入初中数学概念教学为教学研究提供了一个新的视角，将数学概念与人文相融合，使知识技能与情感态度有机整合，落实核心素养，这正是新课程标准下追求素质教育的价值取向，也是数学教育发展的必然趋势.