聚焦两相界面

沈平

Department of Physics, The Hong Kong University of Science and Technology, Hong Kong, China

界面限定了体相。众所周知，在物质的两相分离的界面上会发生许多有趣的现象。在这篇观点性文章中，我将介绍与界面有关的两项最新进展。第一项进展有关海水淡化。由于全球淡水资源不断减少，该进展具有一定的实际意义。第二项进展是关于利用流体动力学中本征模来确定管道流中流体力学边界的位置（这是一个有点令人惊讶的结果，因为这个位置与固-液界面不一致）。同时提供了另一种关于热涨落的观点以及其与介观尺度下管道流的流体边界的位置的联系。

传统的海水淡化工艺流程为蒸发海水，然后浓缩水蒸气制备淡水。这是一个高耗能的过程，因为在蒸发过程中需要大量的相变潜热，而单位能量输入所转化得到的淡水通量一般较低。从微观角度看，蒸发可以脱盐，因为Na+和Cl-都以溶剂化团簇的形式存在于水中，即每一个离子都被一层水分子紧紧包裹着，每单位团簇的大小约为1.1 nm。从溶剂化团簇中提取单个离子所需的能量比水分子从水-气弯月面中逸出所需的蒸发潜热高一个数量级。因此，在蒸发过程中总会有盐分残留。现代海水淡化工艺采用反渗透机制，即使用孔径小于1.1 nm的膜将盐水与淡水分离。制备过程中，需在盐水侧施加高压，这不仅可以克服渗透压，防止淡水扩散到盐水一侧，还可以滤出离子的溶剂化团簇，促使淡水向所需方向流动。在反渗透海水淡化过程中，淡水通量与所施加的渗透压成正比。而由于反渗透膜孔径小，所需的压力非常高，因此单位能量输入所转化得到的淡水通量仍然较低，尽管如此，它比传统的蒸发法仍具有很多优势。

最近有研究者对传统的蒸发法进行优化，取得了海水淡化领域的最新突破。该方法在纳米尺度的通道膜中进行，可以在获得极大的淡水通量的同时，消耗少量的能量[1]。该成果是通过盐水弯月面以及淡水弯月面之间的纳米级分离实现的，这两个弯月面都被限制在纳米级通道中，两侧具有化学势差，淡水侧较低的压力可以驱动淡水流向所需的方向。水蒸气通过努森扩散过程可在短距离内（分离的两个弯月面的距离）快速传输从而产生了大通量的淡水流，同时潜热的回收导致了较少的能量消耗。这是由于蒸发侧弯月面与淡水渗透弯月面均与纳米通道壁接触，通道壁的导热系数通常远高于水蒸气。此外，两个弯月面之间较短的距离也可以加快它们之间的热传递。因此，当蒸汽分子冷凝并释放额外的动能时，相变潜热可以在渗透侧（淡水侧）被大量回收。整个过程如图1所示[1]。结果表明，在膜蒸馏过程中使用碳膜获得的淡水通量比使用高分子聚四氟乙烯（PTFE）膜获得的淡水通量高20倍。这是因为与使用碳膜相比，使用PTFE膜时，两个液体弯月面之间的距离更大。此外，研究人员发现制备过程中80%的消耗潜热能被回收。碳是良好的热导体之一，因此碳膜可以确保纳米尺度通道壁具有相同的等温边界。然而，新的海水淡化工艺[“纳米级蒸发脱盐法”（NED）]的一个缺点是，不能在盐水侧施加高压以进一步提升淡水量，因为对于每个弯月面，施加超过一定值的压力，该弯月面就会破裂。该蒸发过程与液-气弯月面的存在有关，若没有弯月面，则该盐水淡化将没有效果。而液体进入压力取决于孔径大小，因此具有小孔的薄膜可以优化NED工艺。

本文讨论的第二个主题是一个理论问题：在管道几何形态中的流体边界条件和与之对应的流体本征模。本文将把流体边界条件与电动力学的麦克斯韦方程经典物理学的两个基本理论进行对比。电动力学的边界条件可以由麦克斯韦方程组推出，而流体动力边界条件实际上代表了纳维-斯托克斯方程不包含的额外信息。此外，流体动力边界的位置（流体边界条件被施加在此，通常被认为是液-固界面）默认为已知，因为与此相比通常没有更好的选择。但在分子动力学（MD）模拟实验中，众所周知液-固界面附近存在着与液体体相不同的液体密度结构。因此，液-固界面并不一定是流体动力边界。

管道流中的流体本征模是不可压缩纳维-斯托克斯方程在纳维尔滑动边界条件和无外力作用下的解集，可视为实空间粒子的共轭基函数，不同的是对于流体本征模而言边界条件在这里起着至关重要的作用。由于每个流体本征模代表一个自由度，因此其振幅由热动能决定，就像热浴中的点粒子一样。流体本征模的本征值与热动能激发的本征模的衰减时间成反比。此外，由于边界条件可以影响液体内部，因此通过调节通道壁面上的边界条件，就能改变液体体相内的平衡态的性质，如热涨落等。这种潜在性质引出诸多令人深思的统计物理基本问题的可能性尝试。有关流体本征模的一个意外收获是通过分子动力学模拟确定流体本征模的本征值的同时能精确确定流体动力边界的位置。一个有趣的发现是，水动力边界总是在液体区域内，距离固-液界面大约一个分子大小。出现上述现象是因为从分子力学模拟中我们知道，液体分子密度在固-液界面附近呈现出近似固体的层状结构，这种分子结构会对水动力边界产生影响。令人惊讶的是，流体边界是清晰的，它可以准确地反映在连续介质力学中得到的流体动力学模型中。

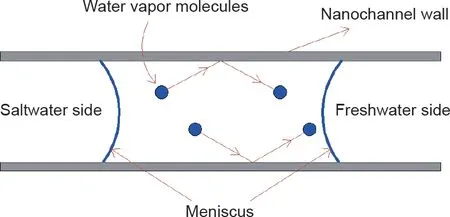
图1. 纳米级蒸发脱盐方案的示意图。化学势梯度：例如，淡水侧的压力低于盐水侧的压力会驱动净水流量从左边流向右边。

最近的一项研究工作指出在Navier-slip边界条件下，二维（2D）通道几何形态中具有完备的流体本征模的解析解[2,3]。流体本征模将液体速度矢量作为空间坐标的函数，由沿两个方向周期性排列的涡对和反涡对组成。具体的例子如图2所示。每个水动力模型有三个参数：滑移长度、流体边界位置和流体本征模的本征值。这三个参数通过色散关系联系在一起。在给定的时刻将流体本征模的解析式投影到分子动力学模拟的速度模型上，然后记录分析其自相关系数随时间的演化，便可以求出流体本征模的本征值。此外，通过将两个不同的流体本征模相乘，并从通道中心向通道边界积分，便可以从积分消失的点来确定流体边界的位置。因为任何两个不同的流体本征模应该是正交的，所以流体边界位置便可以被唯一地确定。滑移长度可以由色散关系计算得到。

流体本征模的完备性可以被用来以另一种方式表示涨落耗散定理[2]：

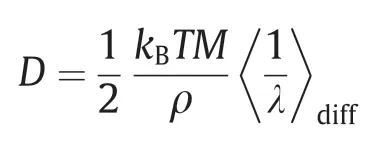
式中，D为自扩散常数；T为温度；kB为玻尔兹曼常量；ρ为质量密度；M为流体本征模的面密度；λ为流体本征模的本征值，单位为时间倒数。尖括号中的量表示1/λ的平均值，代表了在排除衰减时间为分子碰撞时间尺度内的本征模的平均。研究表明，利用上述方法计算的扩散常数与分子力学模拟得到的扩散常数仅相差几个百分点。

沿着通道轴x方向和横向z方向的流体本征模是周期性的。因此，如果我们在通道壁面上对边界条件做出调整，例如，周期性地改变滑动长度的大小，那么边界条件不仅会选择与边界周期性相适应的部分流体本征模，还可以通过阻止它们沿着x方向横向平移来锁定这些相对应的流体本征模的相位。通过这种方式，热涨落，如扩散常数会沿x方向进行周期性变化。这种变化的强度预计将会沿着远离管道边界方向呈指数衰减，衰减的长度与边界条件的周期长度大致成正比。因此，这种效应在介观通道中应当十分明显，例如，在微流体中，如果边界条件调制周期与通道的截面尺寸可以相比拟。

图2. 水动力模型的速度流线图，涡旋对和反涡旋对在x和z方向上都以周期形式出现。

水动力本征模完备集可作为非线性水动力问题求解的基函数，如湍流的产生。该本征模完备集具有满足水动力边界条件的优点，因此在水动力问题中优于其他类型的基础函数。这个方向的研究已经在进行中。