半分布式水文模型模拟土壤含水量的研究

朱悦璐，熊俊飞，邓 炜

(南昌工程学院 水利与生态工程学院，江西 南昌 330099)

土壤含水率是水文、生态、农业以及岩土工程领域的重要参数[1-3]，不同学科对该指标研究各有侧重。例如农业工程中，研究人员重点关注土壤水分变化、判断作物长势、评价农业干旱等问题[4]；岩土工程领域则更多偏向于土中水分变化导致的工程灾害，如地基沉降、边坡稳定等问题[5-6]。可见土壤含水率的测定作为某一研究的“中间环节”，对后续研究结果的正确性至关重要。目前测定土壤含水率的方法可分为两类：其一为单点小尺度测定，其二为大尺度卫星遥感测量技术[7]。

单点小尺度测定法[8-9]对于某点土壤含水率可以较为准确的测定，但无法对某一区域内土壤含水率的变化进行连续监测，只能依靠一点或几个具有代表性的测点表征整个区域含水率的变化，若要获得更精确的数据，则需要连续密集野外作业，这会导致采样成本过高且数据同步性较差。

而基于卫星数据反演的现代遥感技术在一定程度上可以解决上述问题，该方案核心之一是对遥感数据进行光谱分析。这类研究多集中在通过光谱建立土壤含水率回归模型[10]、某类土中特殊光谱与含水率对应关系[11]、基于光谱建立土壤含水率反演模型[12]等方面。目前，国内已有研究团队应用无人机高空摄影对试验区含水量进行监测，为防治土壤盐碱化、农业灌溉方案制定等提供信息指导[13-14]，该技术本质上也是一种小尺度的遥感反演。但应该注意到，上述遥感反演分析结果并不具有普适性，事实上，目前尚无一种土壤含水率测定手段可以同时满足不同研究对象。进一步，在更大尺度中，例如流域尺度评估农业干旱风险问题[15]，受传感器限制，遥感卫星只能在某些特定平坦空旷场合获得可靠数据[16]，因此难于精确指导农业生产，而低空雷达扫描范围又不足以支持流域尺度，若要扩大监测范围则会提高相应成本[17]。此外由于卫星用途、运行轨道等原因，在现阶段，仅为某一课题，通过卫星遥感获取特定区域长系列逐日土壤含水率数据，在我国大多高校或研究机构仍不现实。

基于上述讨论，本文拟采用大尺度陆面水文模型VIC为工具，通过气象数据及下垫面数据建立流域尺度水文模型，模拟生成研究区各网格内逐日土壤含水量，在此基础上，从模型内和模型外分别对模拟结果进行检验，以确保满足工程精度。该方案区别于传统方法，第一可以在基于实测资料基础上，模拟整体区域土壤含水率，数据结构在空间上具有流域尺度整体性；第二由于构建水文模型的气象资料更容易获取，且下垫面数据在一定时期保持时空一致性，因此可以通过较小的成本生成连续土壤含水率数据。本研究所用方法，可以在流域尺度构建具有时空连续分布特性的土壤含水率数据库，为相关工程提供数据基础。

1 水文模型构建

1.1 研究流域

本文选择渭河流域作为研究区，地理坐标为东经106°20′～110°37′，北纬33°40′～37°18′，其地势东西高于南北。按照0.5°×0.5°经纬度将流域划分为75个网格，全流域包括21个气象站点和5个水文站点，如图1所示。

1.2 气象数据

气象数据输入时段为1980—2015年，包括日最高气温、最低气温、降水和风速。分布式水文模型运算中，各个网格的数据相互独立，考虑到距离作为降水空间分布的最重要因素，本研究采用距离权重方案，将21个气象站点数据插值到各网格中心，其公式为

(1)

式中n为格网内站点数；di为第i个站点至每个网格中心点的距离；Pi为第i个站点的实测气象数据，即为每个网格插值后所生成的气象数据。

1.3 植被参数

我国的地类代码为三级分类，共有6大类67个小类。该分类方法与VIC模型采用的Maryland全球1 km陆面覆盖类型分类不同，因此在构建模型下边界条件时，本研究具体的处理方法是将土地利用类型图中多个子项合并成VIC模型中一种植被分类，使其与Maryland发展的陆面覆盖类型参数库相同。

应用Arcgis提取图2中每个网格的信息，并对覆盖类型进行统计，其中i为陆面类型分类号，Vi表示第i类植被在网格内所占的面积，满足公式

(2)

应用式(2)对研究区75个网格内植被信息逐一计算，进行数字化处理，每种信息对应不同的颜色和相应的数据以供模型读取；其制作过程以80s植被分布为例，如图3所示。

上述文件中，不同植被类型对应不同根区深度，各植被12个月的叶面积指数则通过VIC模型从植被参数库文件调取，该套数据可以反映流域真实植被覆盖情况。

1.4 土壤参数

本研究选取的VIC模型网格土壤参数来源于NOAA(The National Oceanic and Atmospheric Administration)提供的全球5′土壤质地分类描述，共有12类，分别为砂土、壤质沙土、沙壤土、粉质壤土、粉土、壤土、沙质粘土壤、粉质粘土壤、粘土壤、沙质粘土、粉质粘土和粘土。

图1 水文模型网格划分

图2 研究区植被参数

图3 构建数字化植被类型图

在模型运行过程中，各土壤类型分别包括53种参数，整体可分为两类，一类是与土壤特性有关的参数，共有47个，另一类是需要对比实测输出结果进行调整的参数，共有6个。第1类参数一旦研究区域选定，当土壤结构已知时，即标定为常数。第2类参数在研究区域选定后，要根据流域土壤实际情况进行调整，调整结果的好坏，直接影响最终模拟精度，这一工作即为模型参数率定。

1.5 参数率定

参数率定是保证模拟结果正确的重要环节。VIC模型需要率定的参数有6个，分别为B，Ds，Dm，Ws，d2，d3。以总量精度误差BLAS%、纳什效率系数NES作为判断函数，其中BLAS代表模拟和实测值在数量上的拟合程度，NES代表模拟值和实测值在趋势上的拟合程度。前者绝对值越小，模型模拟精度越高，后者越接近于1，模型模拟精度越高。其表达式如下：

(3)

(4)

其中Qsim.t和Qobs.t分别为径流序列的模拟值和观测值。

1.6 汇流模型

采用Dag Lohmann研发的汇流程序构建汇流模型，共有7类文件，其中流向文件是汇流模型的核心，它包括汇流方向、网格大小、经纬坐标、流域形状等信息，其余6类为可选项。

该程序分别利用单位线法和圣维南方程计算坡面汇流和河道汇流，整个汇流过程假定为线性，网格内的水分流入相邻8个网格中的一个，这一过程由上游至下游，直至汇入流域出口断面。

对于坡面汇流，不论任何土壤，都假定由降雨引起的快速产流和慢速产流两部分组成，其表达式为

(5)

其中Qs(t)为快速产流，QF(t)为慢速产流，

对于河道汇流，假定由地表产流和地下产流两部分组成，并应用圣维南方程计算，其表达式为

(6)

式中C为波速，D为扩散系数。参数C，D决定了水流在河道间流动的性质，该值可通过实测获取。

1.7 模型运行

上述气象数据、植被数据、下垫面数据以及汇流程序整体上构成了VIC模型的运行环境，利用本文准备的前处理数据，即可驱动VIC模型模拟长系列日土壤含水量。

2 结果与讨论

2.1 模型参数率定结果

本文选取渭河上游林家村站、中游魏家堡站、下游华县站、以及两大支流张家山、状头控制站作为率定对象，通过调整参数，以式(3)～(4)为标准对比模拟值和实测值。率定结果表明，林家村站NES=0.88，总量精度误差BLAS=4.4%，魏家堡站NES=0.85，BLAS=0.62%，该结果可以达到一般工程要求，如图4所示。其余各站点参数率定结果及指标类似，结果见表1。

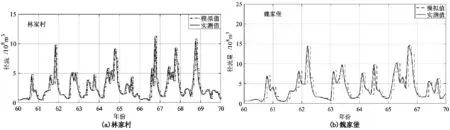
图4 各站率定结果

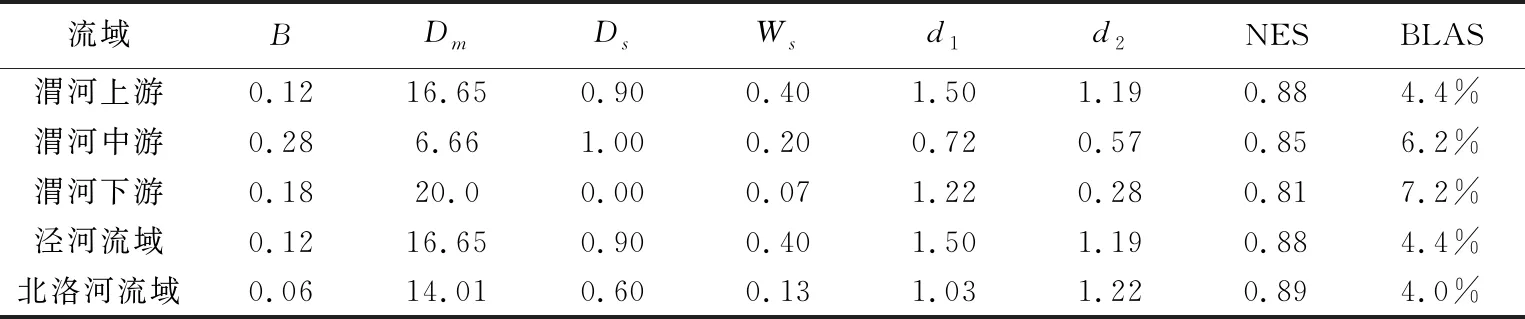
表1 研究流域最终参数方案

应用上述全流域优化后的方案驱动VIC模型，对全流域经行模拟，整体模拟结果NES=0.81，BLAS=6.9%，这一结果满足工程要求，在全流域尺度下，模型通过率定。

2.2 模型参数验证结果

为验证上述参数的合理性，选择紧接率定期后一半时期作为验证期，将表2各子流域参数代入VIC模型。渭河干流上中下游、两大支流验证期NES、BLAS检验结果分别为：(0.84，5.3%)，(0.85，6.2%)，(0.78，7.9%)，(0.86，5.0%)，(0.87，4.3%)，各流域模拟效果如图5(a)～(e)所示。若以各小流域验证结果平均值计算全流域模拟结果，此时NES=0.84，BLAS=5.7%，该值比率定期效果更好，与实际经验不符。

图5 各流域验证期实测模拟对比

进一步的，以华县+状头站径流之和作为渭河流域出口断面对全流域进行验证，模拟结果为：NES=0.81，BLAS=7.3%。如图5(f)所示，这一验证期结果与率定期结果自洽，且满足一般工程精度，因此认为模型在全流域通过验证。

上述相同参数所得出不同模拟结果的现象并不矛盾，这是由于采用不同计算方案所造成的，若直接采用各个小流域模拟结果平均值作为全流域模拟结果，由于没有考虑各小流域径流量、面积等要素在全流域的权重，因此计算结果不如对出口断面进行检验效果准确。

2.3 土壤含水量模拟结果

模型通过率定和验证后，即可用本文所生成的全套参数驱动VIC模型模拟研究区土壤含水率，该含水率数据为1985—2015年各网格上、中、下3层土逐日土壤含水量，共12 784组，保存在输出文件中，将这些数据单独提取，编制为Excel表格，即形成滑坡体所在网格含水量数据库。

为进一步验证该数据库的正确性，选用1981—1991年宝鸡土壤监测站的实测含水量数据进行验证。该站在流域内所处位置如图6所示。

该监测站在上述时段内，每月18日实测一次，10年共有120个土壤含水量数据，以含水量数据库中同时段月平均数据与实测数据进行对比验证，其结果如图7所示。

从图7可以看出，网格模拟含水量和实测含水量在月尺度下，变化趋势基本相同，但二者数值相差较大，网格的平均含水量深度在300～700 mm之间，而站点实测含水量数值在150～400 mm之间，模拟值在整体上高于实测值。归因分析认为，这种系统性偏差主要在于模拟土层和实测土层的最大深度不同，受现场检测手段、监测目的限制，站点最大监测深度为500 mm左右，而本文构建的水文模型3层土平均厚度约为3.5 m，二者相差7倍左右。

2.4 模拟结果讨论

考虑到月尺度下网格平均含水量可能会掩盖某些关键信息，例如极端降雨或者干旱所生成的偶然极值，因此选择相同时间点的模拟值与实测值逐一对比以判断模拟效果，如图8所示。由图中可以看出，相同时刻含水量模拟值和实测值分布与月平均值对比具有类似趋势，即整体上模拟值大于实测值，但二者散点图分布更为紧密，图中已无法直接判断有无系统性偏差；这表明同时刻逐一对比效果好于平均值对比。

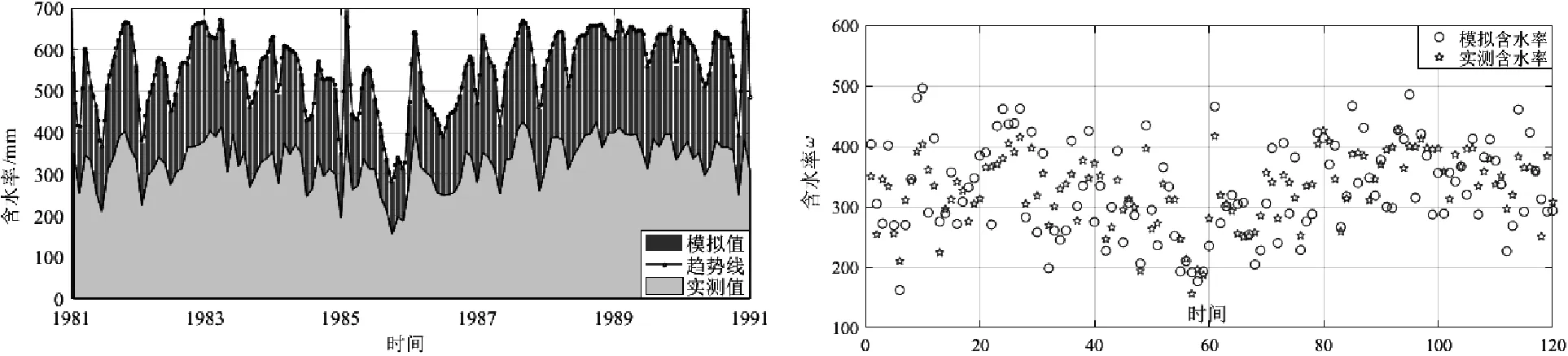
图7 土壤含水量实测模拟对比 图8 土壤含水量实测模拟逐一散点对比

将120组“实测-模拟”含水量数据应用SPSS软件进行统计分析，取最大值、最小值、均值、中值以及标准差等5个量作为统计检验指标，其结果如表2所示；从极值和均值的角度来看，模拟结果和实测结果相差不大，模拟效果较好。

表2 含水量统计分析表

对上述结果做进一步相关性分析，其结果表明，模拟值序列和实测值序列相关性尚好，相关系数R2=0.749 2。各实测值散点与对应模拟值散点差值绝对值基本在±100 mm之间，平均误差约为15.2%。差值最大绝对值为108.1 mm，最大误差为32%。考虑到模型的不确定性，该极端偶然误差可以接受。如图9所示。

图9 土壤含水量相关性分析及差值表

为考察上述含水量误差的来源，按照渭河流域实际气候条件，将该数据按月份划分为旱季和雨季，其中1至3月为旱季，6至8月为雨季。分段考察两组数据的相关性，如图10所示。分析结果表明，含水率实测值与模拟值相关系数旱季R2=0.612 5，雨季R2=0.927 9；雨季模拟结果远好于旱季，因此可以认为，造成含水量模拟值与实测值误差的主要原因是旱季土壤水分模拟不准确。事实上大量前人研究结果表明，VIC模型在湿润地区模拟效果要好于干旱地区，本文所述土壤含水率模拟结果亦是该结论的一个特例。

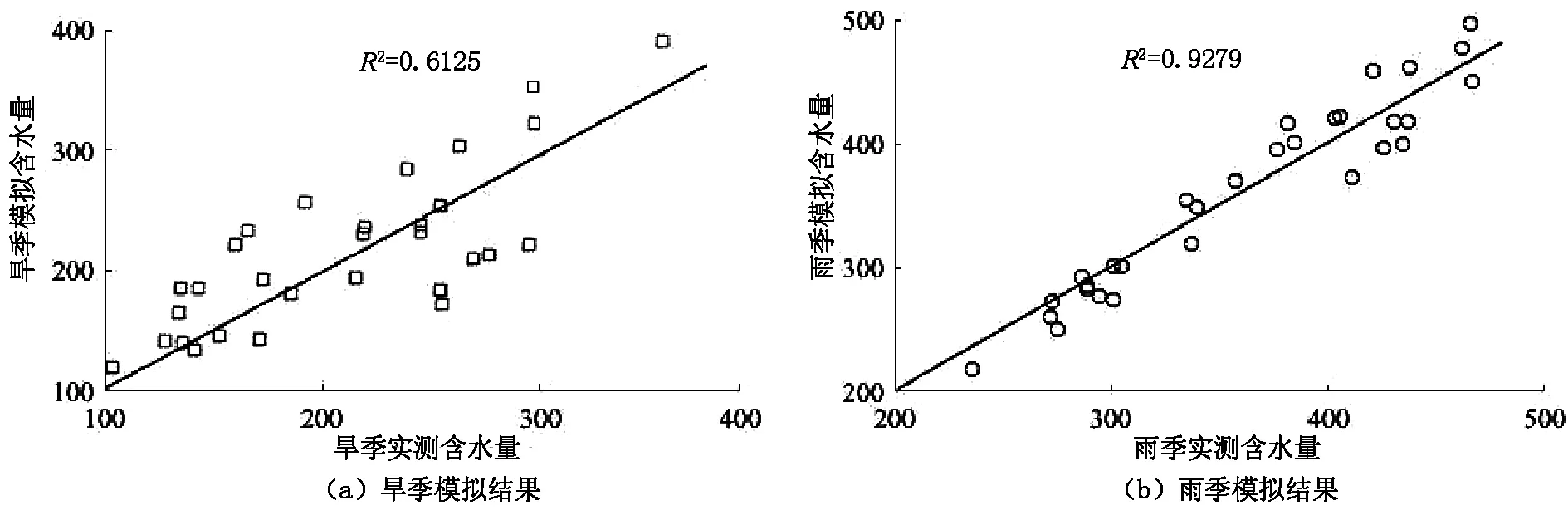
图10 土壤含水率旱季相关性分析，雨季相关性分析

至此，本研究以上述方案生成的土壤含水量数据，在流域尺度、区域尺度和网格尺度上皆通过检验，在精度上可以满足工程要求。网格内土壤含水量模拟值与实测值的检验结果表明：(1)VIC模型模拟的土壤含水量在长时间范围内，变化趋势具有代表性；(2)在具体对应的时间节点上，模拟效果要好于月平均趋势对比；(3)在季节性对比中，雨季模拟效果要优于旱季模拟效果。上述结论与VIC模型区域模拟的传统经验相符，可用于指导实际工程。

3 结束语

本文以实测气象数据和下垫面数据为基础，应用VIC模型模拟生成研究区长系列日土壤含水率数据。这一工作的核心在于将一种较为容易获取的资料转为现阶段某些区域较难获取的数据，可为监测土壤含水率困难的偏远地区提供一种有效的解决途径。为保证水文模型模拟在大尺度条件下的准确性，通过模型内参数率定、参数验证，模型外实测站点对比分析等手段对结果进行检验，认为本研究方案生成的土壤含水率可满足一般工程精度。本文主要结论如下：

模型参数率定结果表明，渭河干流上中下游，和两大支流泾河北洛河NES均大于80%，BLAS小于10%，全流域整体率定结果NES=0.81，BLAS=6.9%，模型在子流域尺度和全流域尺度均通过率定。

模型参数验证结果表明，各子流域验证期NES均大于75%，BLAS小于10%，全流域整体验证结果NES=0.81，BLAS=7.3%，该结果比率定期稍差，但符合水文模型模拟的一般规律，模型在子流域尺度和全流域尺度通过验证。

120组站点实测土壤含水率与其所在网格土壤含水率月平均值对比结果表明，二者具有相同趋势但数值相差较大，整体上模拟值大于实测值，二者相差7倍左右，归因分析认为，这种系统性的偏差来自于土层深度不同以及网格月平均值所带来的误差。

实测值与模拟值在相同时刻的逐一对比结果表明，序列相关系数R2=0.7 492，平均误差为15.2%，最大偶然误差为32%，这一结果要远好于平均值对比，可满足一般工程精度。分季节逐一对比结果表明，含水率相关系数旱季R2=0.612 5，雨季R2=0.927 9，可以认为，造成模拟整体偏差的另一原因在于VIC模型对干旱区域模拟的不准确，这一结论与传统的经验相符合。