基于形态滤波的接地网拓扑检测

王文东 胡绪权 徐正玉 王浩文 付志红

（1. 重庆大学电气工程学院 重庆 400044 2. 重庆璀陆探测技术有限公司 重庆 402660 3. 长江师范学院 重庆 408100）

0 引言

我国普遍采用碳钢作为接地网材料，常年埋于地下容易发生腐蚀，致使其电气性能恶化，严重时直接危及电网的稳定运行[1-6]。查找接地网的断点及严重腐蚀段已成为电力部门一项重大的预防事故措施。国家能源局给出了DL/T 1532—2016《接地网腐蚀诊断技术导则》，用于指导敞开式变电站、换流站等电力工程接地网腐蚀状态的评估[7]，导则给出的方法要求接地网的全部或者部分拓扑结构已知。

目前，接地网拓扑结构探测方法主要有探地雷达法[8]和电磁场分析法[9-12]。探地雷达探测效果容易受目标体尺寸、深度和周围介质的影响，如何准确地从回波数据和图像中识别接地网结构有待进一步研究。文献[9]提出了一种基于电磁场理论的方法，使用特种电源通过引下线向接地网注入和抽出数百赫兹异频正弦电流，接收线圈采集地表磁场，利用模拟前置放大器、工频陷波器和带通滤波器从背景噪声中分离出感应磁场，根据地面磁感应强度峰值位置定位导体。但实际测量得到的磁场数据受地面设备和地下管线等干扰会出现异常凸起和跌落点，磁场峰值定位会导致对导体的漏判和误判，而且远离电流注入点的区域磁场峰值不明显，难以识别，需要对接地网分区分块测量。

基于电磁场分析理论，文献[13-15]研究了基于磁场计算的网格定位方法。文献[13]揭示了变电站接地网正逆问题的内在联系，采用正则化方法计算接地网回路电流判断腐蚀情况，但求解过程复杂。文献[14]提出了一种微分法，利用磁场形函数水平分量偶数阶导数和垂直分量奇数阶导数的主峰特性，对注入电流后接地网上方磁场测量数据进行滤波和数值微分处理，诊断得到精确的载流网格拓扑结构。但微分对噪声敏感，会放大数据测量误差，降低了抗干扰能力，因此对数据的精确性提出了很高的要求。文献[15]结合磁梯度张量特征算子将磁场测面数据的边缘表征为梯度矢量模极大值，引入小波边缘检测场位分离方法识别接地网孔。但计算梯度进行边缘检测同样依赖测量数据的精确性，而且只能处理磁场垂直分量。

数学形态学作为一种行之有效的非线性滤波工具，广泛应用于图像处理[16]、电弧识别[17]、信号分析[18]、电力系统保护[19]和局放检测[20]等领域，但目前尚无针对形态学接地网拓扑成像方法的研究。组合形态学滤波器能够滤除白噪声脉冲噪声，在信号伴随严重噪声甚至发生畸变的情况下，依然可以识别基本几何结构，实现从复杂电磁环境下磁场数据中提取接地网骨架和重建拓扑。

本文提出了一种基于形态滤波的接地网拓扑结构检测方法，避免了复杂的磁场计算，解决了弱磁场峰值难以识别和强干扰下易误判的问题，实现了直接提取出精确、完整的接地网拓扑结构。

1 载流导体的空间磁场分布

1.1 载流单导体模型

接地导体的尺寸相对于地下空间而言很小，将单段接地导体等效为不计尺寸的有限长载流直导线。在实际测量中，相对于测量系统所采用的坐标系，接地网导体的走向可能是未知的。因此考虑一段与平面坐标轴有任意夹角α的有限长载流直导体，其模型如图1所示，导体埋深为h，土壤为单层均匀土壤，磁导率为0μ。P是地表任意一点，与导体两端点连线同导体夹角分别为θ1、θ2，与导体垂直距离r，磁感应强度方向矢量e。

图1 单根有限长载流导体模型Fig.1 Single conductor current-carrying model with limited length

以导体轴向作为y′方向建立x′Oy′坐标系，导体流过电流I，忽略土壤的散流效应，由毕奥-萨法尔定律和坐标变换方法计算得到任意坐标系xOy下载流导体在空间P点的磁感应强度为

其中

式中，(x,y)和(x′,y′)分别为xOy和x′Oy′坐标系下的坐标；(x0,y0)和(x1,y1)为直导体两端点坐标；ex、ey为方向矢量。

1.2 载流接地网模型

网格状接地网由多段导体组成，地表面磁场分布可以描述为各段载流导体的叠加。由式（1）可得载流接地网在空间中产生的磁感应强度水平分量为

式中，n为导体总段数；Bxi和Byi分别为第i段导体产生的空间磁感应强度x、y分量。

当导体与某一坐标轴平行时，式（1）中该方向的感应磁场为0，该导体的感应磁场便不会在式（2）中体现，故只采用单一方向的磁感应强度无法全面描述载流接地网所有导体的空间磁感应强度分布。因此，本文采用x和y方向磁场共同描述。将两方向磁感应强度Bx、By求矢量和，使用磁通密度模值描述载流接地网的空间磁场分布，可以兼顾沿各个方向埋设的导体，磁通密度模MBf为

对于如图2a所示的网格大小为5m的5×5的接地网模型，选取左下角A为电流注入点，右上角C为电流抽出点，埋深h=0.8m，计算出其空间磁场分布如图2b所示。

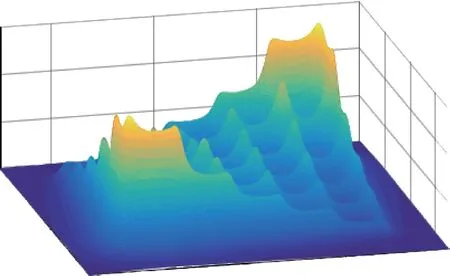
图2 载流接地网地表磁场分布Fig.2 Magnetic field induced by current-carrying grids

在接地网区域(x,y)∈R上，对于任意的常数x0、y0，当磁通密度模梯度∇MBf满足则称在该点取得局部极大值。

磁通密度模局部极大值在导体正上方取得，局部极大值点的集合构成连通图，即为载流导体构成的接地网拓扑。由于接地网电流分布不均，远离电流注入点的导体正上方的局部极大值很快衰减到全局极大值的1/10左右，甚至小于注入点附近的局部极小值，因此弱磁场区域拓扑难以被有效识别。

2 形态滤波接地网拓扑提取方法

数学形态学的基础是集合论，具有完备的数学基础，其本质是非线性滤波器。形态滤波器可以简化图像数据，保持基本形状特性并去除不相干结构[14-16]，因此形态滤波方法可以很好地排除异常数据干扰，获得接地网拓扑结构。

2.1 形态滤波接地网拓扑提取原理

一般而言，灰值数学形态学的处理对象是图像信号波形的拓扑特性，本文将磁通密度模值MBf函数视为灰度图像，作为输入信号。

对于输入信号MBf(x,y)和结构元素g，定义形态学运算操作。

1）腐蚀

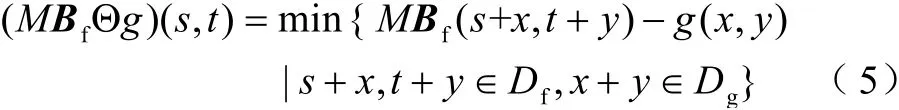
式中，（x,y）、（s,t）分别为形态学运算前后的坐标；Θ为数学形态学“腐蚀”运算符；Df和Dg分别为信号定义域和结构元素定义域。

从几何上讲，腐蚀运算使用结构元素在信号下部进行滑动，消除信号中向下的尖峰，起到滤波效果。

2）膨胀

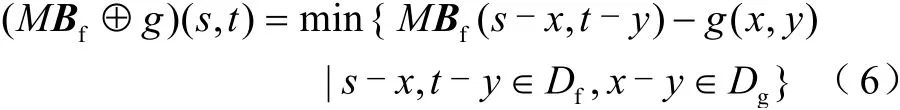
式中，⊕为数学形态学“膨胀”运算符。

膨胀运算是腐蚀运算的对偶运算，当结构元素在信号定义域内滑动时，利用结构元素的反射，在当前结构元素的定义域内，上推结构元素，使结构元素超过信号的最小值，从上部对信号进行滤波，消除向上的异常尖峰噪声。

（1）先腐蚀再膨胀的迭代运算为开运算

式中，○为数学形态学“开”运算符。

（2）先膨胀再腐蚀为闭运算

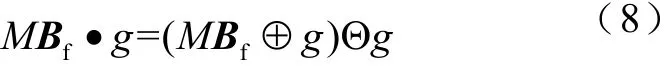
式中，•为数学形态学“闭”运算符。

接地网拓扑是一个封闭图形，由基尔霍夫电流定律和基尔霍夫电压定律可知，电流的流通路径也必然是闭合的，因此不存在孤立的支路和节点。地表磁场测量数据若出现孤立的极大值区域或不连续的支路，必然由噪声或干扰导致。当接地导体出现断点或严重腐蚀，其上电流为零或近似为零，整段导体上方磁场降低为背景磁场，不存在段中局部磁场跌落的情况，如果出现，也必然为噪声或干扰导致。

形态学开运算作为一个基于几何运算的滤波器，消除比结构元素小的孤立点、毛刺和小桥，而总的位置和形状不变。开运算只消除磁场数据中孤立的噪点而不改变原有拓扑结构。闭运算通过填充凹角来滤波，能够填平前景内的小裂缝，当载流导体正上方磁场出现异常跌落，闭运算对其进行填补，增强连接，保证拓扑的完整性。

结构元素的大小和形状决定了滤波效果，选择合理的结构元素能够有效滤除噪声并保持原信号的结构特征。

2.2 改进的分水岭算法

分水岭算法是一种基于拓扑理论的数学形态学分割方法，将输入信号各点的值视为该点的海拔，将输入信号曲面视为地形图，运用地理学上的测线重构思想找到边界实现分水岭变换[21]。

经典的分水岭算法是L. Vincent等提出的浸入模拟法[22]，局部极小值点作为集水盆的起始点，随着水位不断上升，集水盆的区域向外扩散，到一定高度后两个或多个集水盆发生汇合，汇合处即为分水岭。

使用分水岭算法处理接地网地表感应磁场函数，可以获得精确、封闭、连通的拓扑结构图。但是由于噪声影响和插值方法限制，实际数据中会出现大量伪极小值，进而产生伪分水岭，拓扑图上表现为伪导体。

分水岭算法示意图如图3所示。浸入式分水岭算法要求浸水阈值h1、h2，地表磁通密度模局部极大值的变化范围较大，不恰当的阈值会导致有用分水岭丢失。

图3 分水岭算法示意图（浸入模拟）Fig.3 Watershed algorithm(immersion simulation)

针对感应磁场的数据特点，进行分水岭算法处理之前首先进行背景补偿和信号增强，实现数据规范化。对于磁通密度模函数MBf，使用滤波器W对对其进行卷积。

滤波器wuv=1，U、V为卷积核大小，卷积核需略大于最大网格间距，以使其能够同时覆盖局部极大值和局部极小值，保证后续数据增强效果。对函数MBf等距抽样选点得到一个二维矩阵，卷积获得该点附近领域U×V点个值的累加和，实际上为避免峰值影响，应选取其中值最小的20%的点求算数平均，定义求取到的点(x,y)的背景值为MBfh(x,y)。

背景值越小，说明该点越远离导体正上方，越远离电流注入和抽出点。使用距离反比法进行背景补偿，点(x,y)处的距离d和补偿函数分别定义为

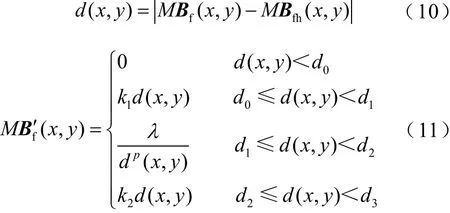
MBf′(x,y)为补偿后的磁场，λ、p、k1、k2取值应使得分段函数连续，一般而言，k1可取3~8之间的的一个常数，k2可取0.8~1.5。全局阈值滤波器d0用于滤除数据中的微小噪点，分界点d1~d3为先验值，根据实验结果确定取值。

图4 a给出了图2b三维图中y=2.5m处的磁通密度模，对其进行背景补偿和数据增强处理，补偿倍数1~6.2倍，d1和d3分别取距离最大值dmax的80%和10%，结果如图4b所示。

图4 y=2.5m磁通密度模规范化结果Fig.4 Normalization results for magnetic flux at y=2.5m

2.3 接地网拓扑结构提取流程

接地网拓扑结构提取流程分为数据预处理和组合形态滤波获得拓扑两个部分。图5给出了基于形态滤波的接地网拓扑提取流程。

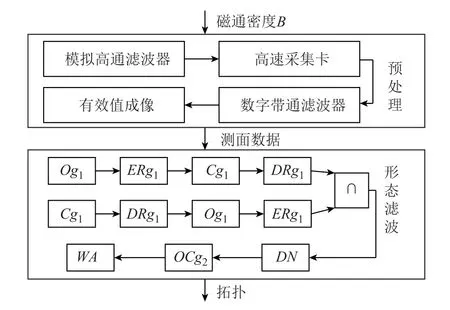
图5 接地网拓扑提取流程Fig.5 Topology extraction process

采集到地表磁场数据后，首先对数据预处理。变电站测量到的磁场数据幅值较小，信号容易被以工频噪声为主的背景噪声淹没。使用模拟滤波器滤除信号中的干扰较强的工频以及低次谐波，再通过高速数据采集卡对信号采样后经过数字带通滤波器获得与激励源同频磁场信号，每个测点保存一个磁场数据幅值用于计算和成像。对原始磁场数据二次曲面插值，近似得到整个测面的数据。再对数据进行高斯平滑，滤除测面上的高斯噪声。

然后构建复合形态滤波器，其构成包括形态开(Og1)、形态闭(Cg1)、腐蚀重建(ERg1)、膨胀重建(DRg1)、数据规范化(DN)、形态开-闭(OCg2)、形态学分水岭边界提取(WA)。

预处理后的数据归一化到灰度值0~255，经过形态开滤波器消除孤立凸起点，形态闭滤波器填充结构裂缝，腐蚀重建和膨胀重建增强数据，数据规范化增强弱磁场区域峰值，小结构元素g2形态开-闭滤波消除数据规范化产生的噪点，通过分水岭算法提取出接地网拓扑。

3 仿真算例

建立图2a中接地网的多物理场仿真模型，仿真模型如图6a所示，导体截面积6cm×5mm，网格大小5m×5m，埋深0.8m，10A电流从A点注入、C点抽出。单层土壤，厚度50m，土壤电阻率50Ω·m，土壤磁导率近似取真空磁导率0μ。图6b给出了仿真结果，将磁通密度模转换得到大小为351×351像素灰度图。对灰度图数据分别使用文中提出的形态学方法、canny边缘检测算子、直接使用分水岭算法处理，结果如图7所示。网格间距为50像素，结构元素尺寸不能大于该值，否则将造成局部极大值之间的粘连；结构元素尺寸同样不宜小于网格间距的1/2，否则不能实现网格中心异常凸起的去除。综合考虑，形态学处理时选择结构元素大小为31。

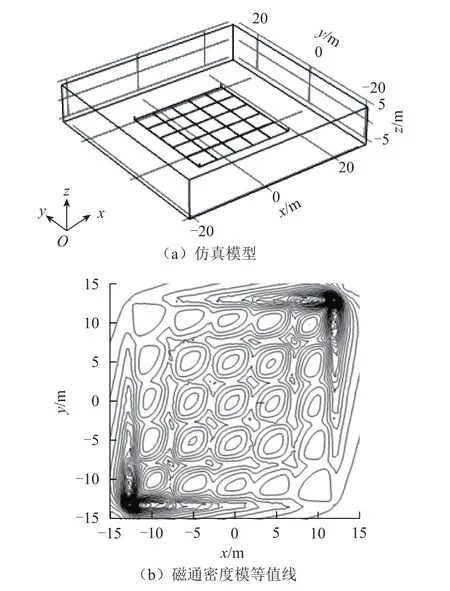
图6 仿真结果Fig.6 Simulation results

图7 拓扑结构提取结果Fig.7 Topology extraction results

可以看出，直接使用canny边缘检测算法处理，存在磁场较弱的区域的接地网结构不能有效识别的情况，而直接使用分水岭算法，同样不能有效识别出弱磁场区域的接地导体，而且存在一定程度的过分割情况。定义识别到的导体段数与导体总段数之比为拓扑完整率，定义识别到“伪导体”段数导体总段数之比为误判率，对比三种方法拓扑提取结果。

仿真结果对比见表1，传统的边缘检测算法canny算子提取的拓扑完整率仅为不到90%，弱磁场区域的拓扑结构丢失，而本文的形态学方法达到了100%。相比于直接使用分水岭算法，形态学处理后提取到的拓扑更完整，而且基本消除了过分割情况。仿真结果表明，数学形态学方法可以有效处理弱磁场区域数据，提取到更完整的接地网拓扑结构。

表1 仿真结果对比Tab.1 Comparison of simulation results

4 实验分析

在实验场开展模拟实验。整个实验接地网长13.6m，宽10.2m，由4×3个网格构成，网格间距3.2~3.4m，接地导体使用60mm×8mm镀锌扁钢，埋设深度0.8m。

接地网模拟实验如图8所示。从图8中A、B两点注入和抽出频率9kHz、幅值9.9A的双极性电流。采用直径15cm，匝数600的接收线圈采集地表感应磁场，选用数字多用表34401A测量和记录接收线圈感应电压有效值。接收线圈感应电压有效值可以表征地表磁感应强度，磁场测量区域应远离电流注入点[4]，选择网格EFGH进行测量，测点间隔10cm。测量区域内，各段导体的正上方均布置测点。

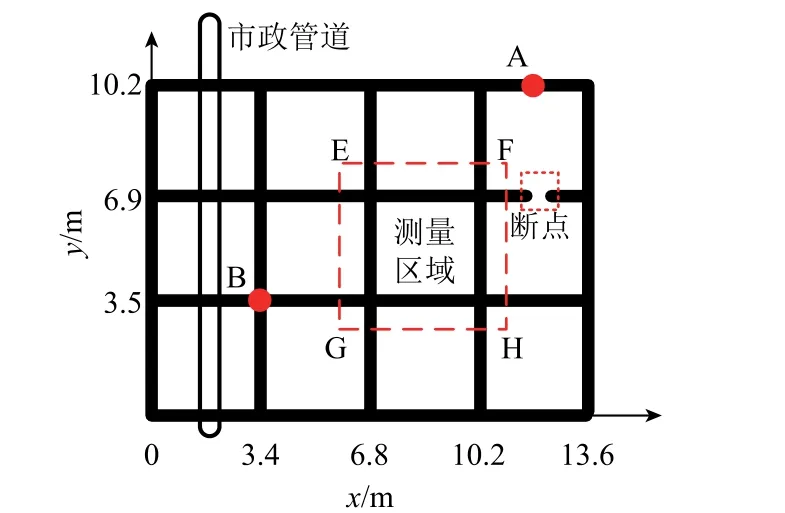
图8 接地网模拟实验Fig.8 Simulation experiment of grounding grids

使用感应电压有效值成像，以1cm为间隔对原始数据进行插值，测量结果如图9a所示。形态学方法处理结果如图9b所示，处理后提取到单像素宽的拓扑结构图。F点靠近电流注入点，直线距离仅为3.6m，磁场受到强干扰导致定位出现较大偏移，其余导体定位较为准确。实际值与测量值对比见表2。

表2 实验结果对比Tab.2 Comparison of simulation results

图9 形态滤波处理结果Fig.9 Processing results based on morphological filtration

将提取得到的拓扑结构与实际施工图纸比较，以网格大小3.4m×3.4m作为基准值计算定位误差。F点距离电流注入点较近，在强干扰的情况下，形态学方法仍然能够定位端点，且误差不超过网格大小的10%。远离电流注入点的区域，各导体和端点的定位误差不超过3%。实验结果验证了使用形态滤波方法提取接地网拓扑结构的可行性。

5 结论

本文提出了一种基于形态滤波的接地网拓扑结构提取方法，通过构建复合形态滤波器，直接从磁场数据中识别和定位接地网。在数据精度有限的情况下得到较为精确的结果。仿真和模拟地网实验结果验证了该方法的可行性，为应用于实际变电站接地网拓扑检测奠定了基础。