考虑饱和效应的无刷双馈发电机功率模型预测控制
魏新迟 许利通 骆仁松 程 明 朱建国
(1. 国网上海市电力公司电力科学研究院 上海 200437 2. 东南大学电气工程学院 南京 210096 3. 南瑞继保电气有限公司 南京 211102 4. 悉尼大学电气与信息工程学院 悉尼 NSW 2006)
0 引言
无刷双馈电机是一种近年来被重点关注的新型交流电机,其有两个交流馈电端口和一个机械端口,通过定子励磁的方式实现无刷化,可在保留普通双馈系统优点的同时大大提高其可靠性,在大容量变速恒频发电领域具有很好的应用前景[1-5]。但是无刷双馈电机的结构和电磁关系较为复杂,导致相应的控制器设计难度较大,亟需对无刷双馈电机的控制技术进行研究,以促进其发展及应用。
无刷双馈电机矢量控制采用传统的双闭环结构,外环调节有功(或转矩)和无功(或磁链),内环调节控制绕组电流的转矩分量和磁链分量。但是这种控制方法将在静态和动态性能间进行折中,从而达到相应的控制效果。直接功率控制(或直接转矩控制)根据控制变量的调节误差计算开关状态来控制变流器,从而将调节误差控制在合理范围内,其控制结构简单,鲁棒性强,动态性能大大提高[10-15]。但该方法使用预设矢量表,无法准确控制功率(或转矩),导致其出现较大脉动。后续有文献研究模型预测控制,实现了功率的精确控制,具有优良的稳态与动态性能[16]。已有文献对无刷双馈电机的饱和建模与特性分析进行了广泛研究。文献[17-19]分别基于有限元法、等效磁路法和等效电路法建立了无刷双馈电机的饱和模型,但是建模方法均较为复杂且并没有进一步考虑控制性能的提升。文献[20]在考虑饱和效应动态建模的基础上设计了独立运行控制器,实现了稳态与动态性能的双提升。然而,现有的无刷双馈电机并网运行控制方法均未考虑电机的饱和模型[6-12]。文献[21-22]表明无刷双馈电机的功率因数较低,饱和对电机参数的影响比传统双馈发电机更大,引起电机定子绕组电流和损耗增加,导致电机输出转矩/功率下降;考虑饱和效应后的计算值与实测值更加接近。因此,研究无刷双馈电机高性能控制,需充分考虑电机饱和效应的影响。
本文提出考虑饱和效应的无刷双馈发电机(Brushless Doubly-Fed Induction Generator, BDFIG)功率模型预测控制策略,在控制器中引入励磁电感估算,明确了影响饱和效应的运行因素,实现了功率的精确控制,保证控制侧电流的正弦度和较低的开关频率。
1 BDFIG的建模与分析
1.1 BDFIG饱和效应模型
BDFIG在任意速坐标系下的动态数学模型可表示如下[23-24]。
电压方程为

式中,上标g代表任意速坐标系;下标sp、r、sc分别代表功率绕组、转子绕组、控制绕组;p为微分算子;R为电阻;u、i、ψ分别为电压、电流、磁链矢量;ωg为任意速坐标系电角频率;ωrp为功率侧转子绕组电角频率;ωrpc为功率侧与控制侧转子绕组相对角频率。
磁链方程为

励磁磁链方程为

其中
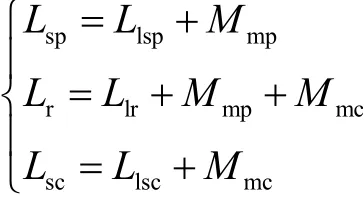
式中,Lsp、Llsp、Mmp分别为功率绕组自感、漏感和互感;Lsc、Llsc、Mmc分别为控制绕组自感、漏感和互感;Lr、Llr为转子绕组自感和漏感。
将式(3)代入式(2),整理得到
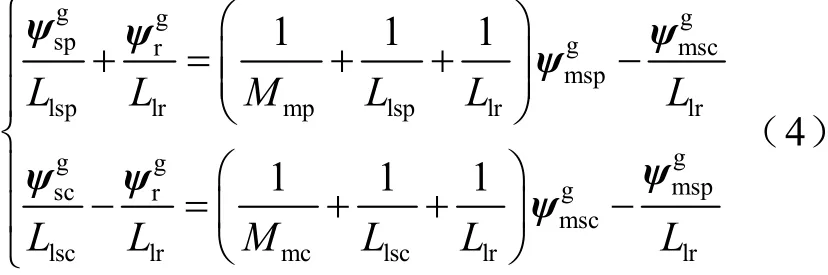
式(4)表明,励磁磁链可由各绕组磁链和电感值计算得到。考虑饱和效应的建模过程中,将励磁电感作为输入变量,每周期依据励磁磁链的数值查表得到实时的电感值。综上,考虑饱和效应的动态模型可表示如下。
电压方程为
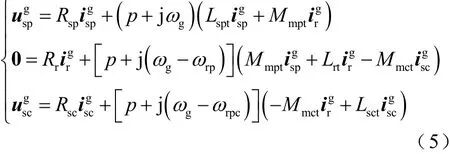
式中,Lspt=Llsp+Mmpt,Lrt=Llr+Mmpt+Mmct,Lsct=Llsc+Mmct。不考虑饱和效应时,Mmpt和Mmct为恒定值,励磁磁链与励磁电流之间呈线性化关系;考虑饱和效应时,Mmpt和Mmct为每周期依据饱和特性更新得到的数值,励磁磁链与励磁电流之间呈非线性关系。
转矩方程为

式中,pp和pc分别为功率绕组和控制绕组极对数。
1.2 稳态模型及功率分析


式(8)中第一个公式的三项分别为功率绕组有功功率、铜耗、气隙有功功率;第二个公式的三项分别为功率绕组无功功率、电感消耗的无功功率、气隙无功功率。式(7)中第三行方程两边同乘以并进行实部与虚部分解,可得

式(9)中第一个公式的三项分别为控制绕组有功功率、铜耗、气隙有功功率;第二个公式的三项分别为控制绕组无功功率、电感消耗的无功功率、气隙无功功率。
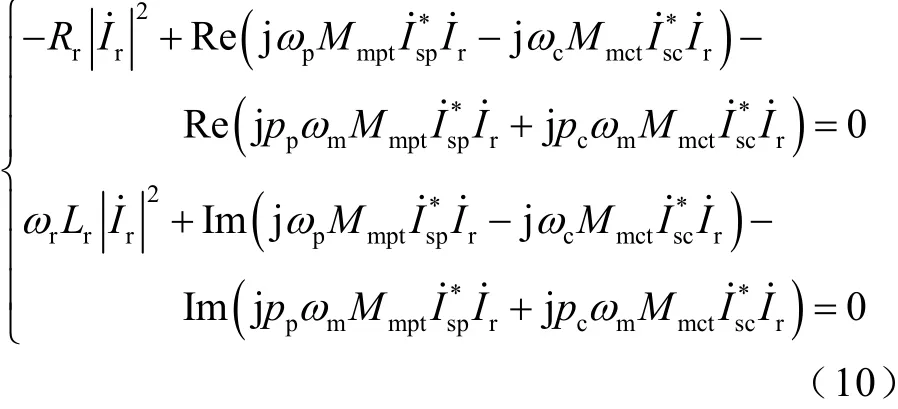
式中,第一个公式的三项分别为转子铜耗、功率侧与控制侧气隙有功功率、转子机械功率;第二个公式的三项分别为转子电感消耗的无功功率、功率侧与控制侧气隙无功功率、转子存储的无功功率。
综合式(8)~式(10),可得BDFIG的有功功率和无功功率分配如图1所示。

图1 BDFIG功率分配图Fig.1 Power distribution diagram of BDFIG
2 功率模型预测控制系统设计
2.1 功率预测模型
基于BDFIG考虑饱和效应的动态模型,可得状态空间方程为[23]

其中

式中,X为状态空间变量V为电压矢量,矩阵A中A11~A33的表达式见附录。
进一步推导得到功率绕组侧的复功率矢量表达式为[23]

其中
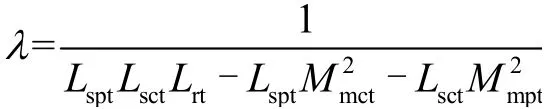
将复功率矢量对每个采样周期进行求导并进行离散化处理,可得BDFIG的复功率预测模型为
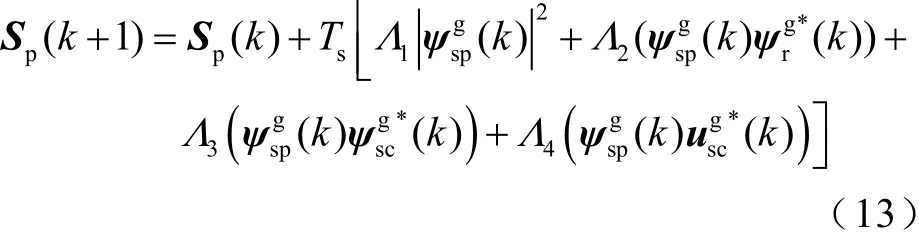
式中,sT为采样周期,k∈N表示采样时刻,Λ1~4Λ的表达式详见附录。
将式(13)分解,得到以有功功率和无功功率分别表示的预测模型为
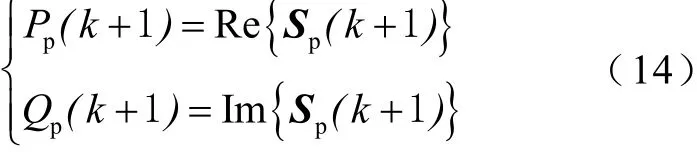
2.2 考虑饱和效应的功率模型预测控制系统
考虑饱和效应的功率模型预测控制系统框图如图2所示,主要包含励磁电感估算、磁链估算、功率估算和预测、价值函数优化四个部分。

图2 考虑饱和效应的功率模型预测控制系统框图Fig.2 Block diagram of the model predictive power control system considering saturation effects
2.2.1 励磁电感估算
本文以级联式BDFIG为例,参数见表1。依据单馈空载实验测点数据,采用多项式拟合得到功率侧/控制侧的励磁电流imsp/c与励磁磁链ψmsp/c关系如式(15)所示,饱和特性曲线如图3所示。

图3 饱和特性曲线(功率/控制侧)Fig.3 Saturation characteristic curve (power/control side)

表1 BDFIG参数Tab.1 Parameters of BDFIG
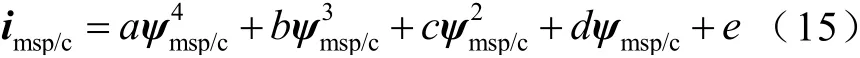
式中,a= 21.61,b= –18.32,c= 5.938,d= 3.912,e=0.002 437。
图3 中,曲线的斜率对应励磁电感Mmp/c的数值,可以看出当励磁磁链大于0.6Wb时,电机逐渐进入饱和状态,曲线出现拐点,斜率值(Mmp/c)变化明显。因此,对于参数依赖性较强的功率模型预测控制,需要在每个周期对励磁电感值进行估算,并作为控制器的输入。
求解磁链方程式(4),可以得到第k周期功率绕组励磁磁链和控制绕组励磁磁链。考虑到一个周期中励磁磁链基本保持不变,相应的励磁电感改变较小,因此可基于第k-1周期的励磁电感得到第k周期的励磁磁链。仿真时,初始状态值采用不饱和励磁电感值。计算式为
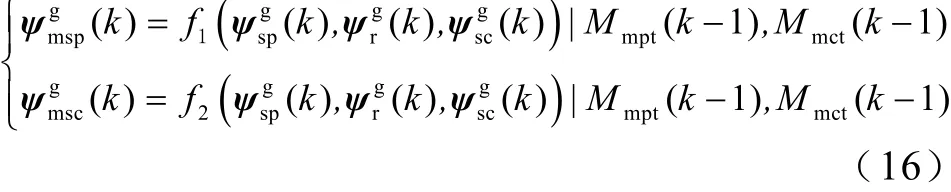
基于图3的拟合曲线,建立基于励磁磁链(横轴)-励磁电流(纵轴)-励磁电感(斜率)数值的lookup表格,通过励磁磁链幅值查表可获得每周期实时的励磁电感值,即
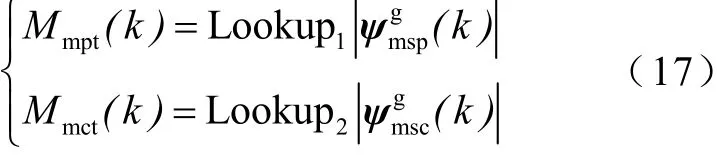
2.2.2 磁链估算模型
为了尽可能减少磁链估算模型对参数的依赖性并考虑饱和效应,采用磁链估算模型为

功率绕组磁链ψsp可通过usp−Rspisp的积分得到,并引入角度偏差与幅值偏差校正。磁链估算模型中引入控制绕组励磁电感、漏感,功率绕组漏感、转子绕组漏感。漏感数值较小且基本不受饱和效应的影响,可认为是恒定值,因此仅有控制绕组励磁电感会影响磁链观测的准确性。将考虑饱和效应的控制绕组励磁电感Mmct作为磁链估算模型的输入。
2.2.3 功率估算和功率预测
基于精确的磁链估算,可由式(12)估算功率绕组的功率,由式(13)计算得到功率预测模型。同样,式中的漏感参数可视为恒定值,将考虑饱和效应的励磁电感参数Mmpt和Mmct作为功率模型的输入。
2.2.4 价值函数优化
为了达到期望的控制目标,设计满足有功功率和无功功率控制目标及开关频率限制的价值函数为

式中,Ppref和Qpref分别为有功和无功功率的参考值;Pp(k+1)和Qp(k+1)分别为有功和无功功率在k+1周期的预测值;Sx(k)和Sx(k+1)分别为k周期和k+1周期施加的开关状态;δ1和δ2为权重系数。
式(19)中,第一项代表有功功率误差最小化的控制目标;第二项代表无功功率误差最小化的控制目标,将有功功率与无功功率控制分配相同的权重,系数δ1=1;第三项代表降低开关频率的控制目标,在保证功率精确控制的前提下减小开关频率,系数δ2=25。
3 仿真分析
基于Matlab/Simulink搭建仿真模型,采用多速率离散仿真的方法[25],将控制器的仿真步长设置为100μs,实际物理系统的仿真步长为设置为2μs,BDFIG的主要参数详见表1。
3.1 动态模型的仿真结果
BDFIG运行于650r/min,控制绕组连接电阻负载,控制绕组给定励磁电压幅值为98V,频率为15Hz。图4所示为动态模型的仿真结果。图4中波形分别为功率绕组电压usp、功率绕组电流isp、控制绕组电流isc、功率绕组励磁磁链ψmsp、控制绕组励磁磁链ψmsc和电磁转矩Te,其中,虚线代表考虑饱和,实线代表不考虑饱和。由图4中的结果可见,在动态建模中考虑饱和效应后,电压、电流、磁链和转矩脉动均明显减小,控制绕组电流波形正弦度更好,励磁磁链幅值保持在适当范围。

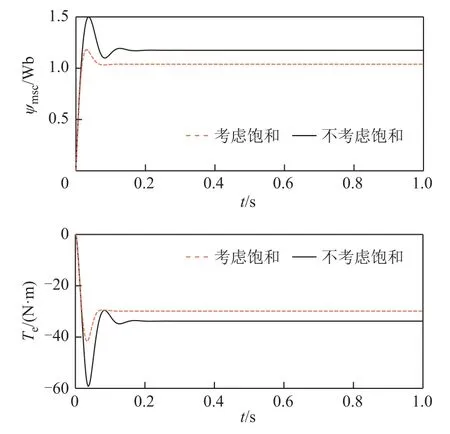
图4 BDFIG动态模型仿真结果Fig.4 Simulation results of BDFIG dynamic model
3.2 功率模型预测控制系统的仿真结果
BDFIG并网运行时,功率绕组磁链较为恒定,为了简化功率模型预测控制器的设计,仅考虑控制绕组励磁磁链/电感的饱和效应。图5a所示为考虑饱和与不考虑饱和的仿真对比(n=650r/min,Ppref=-600W,Qpref=0var),图5a中波形分别为功率绕组电流isp、控制绕组电流isc、控制绕组励磁磁链ψmsc和励磁电感Mmc。可以看出考虑饱和时,控制绕组侧的励磁磁链、励磁电感及电流的数值与不考虑饱和时相差较大。其中,控制绕组励磁电感值约为184.5mH,而不饱和电感值为220mH,表明此时的饱和效应较为明显。表2所示为不同转速下的饱和电感数值,随着转速的上升,饱和电感值逐渐偏离不饱和值,饱和效应的影响增加。图5b所示为无功适量(Qpref=500var)与无功为零(Qpref=0var)的仿真对比(n=650r/min,Ppref=-600W)。给定无功的情况下,功率绕组电流幅值变大,控制绕组电流幅值与励磁磁链幅值变小,励磁电感数值与不饱和电感数值较为接近,此时饱和效应的影响较小。因此,在实际运行中,为了减小饱和效应的影响并保证控制效果,需向BDFIG提供适当的无功功率并使其运行在较低转速。上述结果进一步表明,饱和效应对励磁电感数值和励磁磁链水平影响较大。可以预见,当实际电机运行于较为饱和的状态时,若控制器中的励磁参数仍采用不饱和电感值,将会与电机实际状态时的参数偏差较大,最终导致功率控制出现偏差,电流波形受到影响。
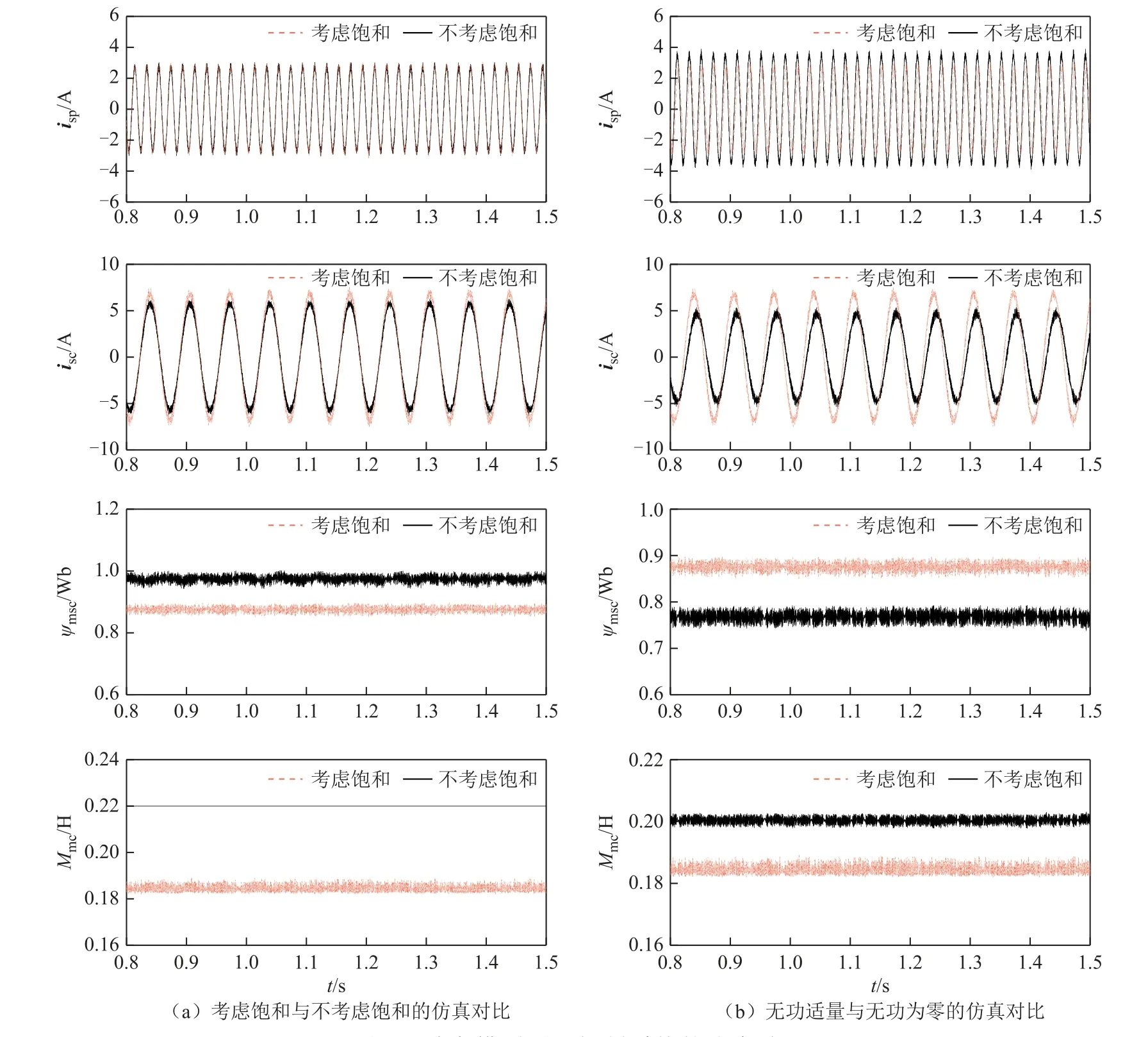
图5 功率模型预测控制系统的仿真结果Fig.5 Simulation results of the power model predictive control system
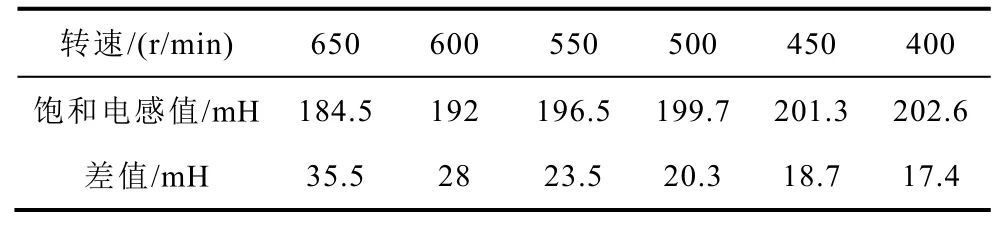
表2 控制绕组励磁电感值Tab.2 Magnetic inductance of control wires
4 实验分析
为了测试考虑饱和效应的功率模型预测控制系统的实际效果,使用图6所示的实验平台进行验证,包括原动机、级联式BDFIG、逆变器、dSAPCE系统等。依据仿真得到的结论,在实验中考虑400~600r/min的运行范围,给定Qp=500var的无功功率,每周期估算励磁电感值作为功率模型预测控制器的输入,尽可能减少饱和效应产生的影响。

图6 无刷双馈发电系统实验平台Fig.6 Experimental platform of brushless doubly-fed system
图7 所示为稳态运行的实验结果,BDFIG运行在400r/min,有功功率参考值为-600W,无功功率参考值为500var,图中波形分别为有功功率Pp、无功功率Qp、功率绕组电流isp、控制绕组电流isc和开关频率n。从实验结果可以看出,有功和无功功率均能很好地跟踪参考值,控制绕组电流较为正弦,开关频率约为1.3kHz。图8所示为变速运行的实验结果,电机转速从400 r/min逐渐上升至600 r/min,有功功率参考值为-600W,无功功率参考值为500var。从实验结果可以看出,控制绕组电流频率随着转速发生变化,而功率绕组频率保持不变,实现了BDFIG的变速恒频运行。图9所示为变速运行且有功功率参考值阶跃变化情况下的结果,电机转速从450r/min逐渐上升至550r/min,有功功率参考值从-400W阶跃至-600W,再从-600W阶跃至-500W,无功功率参考值为500var。从实验结果可以看出,有功功率能够很好地跟踪阶跃给定信号,且无功功率不受影响,说明有功功率和无功功率可实现很好的解耦控制。上述实验结果验证了本文所提控制系统的有效性。

图7 稳态运行时的实验结果Fig.7 Experimental results under steady-state operation
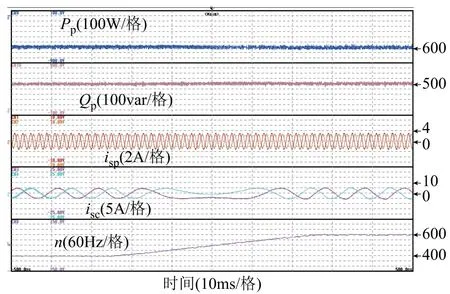
图8 变速运行时的实验结果Fig.8 Experimental results under various speed operation

图9 变速运行且有功功率给定阶跃变化时的实验结果Fig.9 Experimental results under various speed and active power condition
5 结论
本文针对BDFIG,建立了任意速坐标系下考虑饱和效应的动态模型,详细分析了有功功率与无功功率分配,提出了考虑饱和效应的功率模型预测控制策略。为验证饱和模型及本文所提功率模型预测控制策略的有效性,对BDFIG系统进行建模,并搭建了相应的实验平台。实验结果表明,在动态建模中考虑饱和效应后,电压、电流、磁链和转矩脉动均明显减小,控制绕组电流波形正弦度更好,励磁磁链幅值保持在适当范围。向BDFIG提供适当的无功功率并使其运行在较低转速,可有效减小饱和效应的影响并保证控制效果。本文所提考虑饱和效应的功率模型预测控制具有快速的动态响应,能够实现有功功率和无功功率的精确控制及解耦控制,保证控制侧电流正弦度和较低开关频率。
附 录
式(11)矩阵A中A11~A33的表达式为


