脉冲神经网络算法及其在扑克游戏中的应用

董丽亚，何 虎+，王麒淋，杨 旭

(1.清华大学 微电子与纳电子学系，北京 100084；2.北京理工大学 软件学院，北京 100084)

0 引 言

脉冲神经网络(spiking neural network，SNN)[1]是一种极具生物可解释性的仿生型人工神经网络，不同于现在主流神经网络采用的“统计+计算”的方式，脉冲神经网络通过拟合生物神经元机制，模拟生物神经网络的结构和信息加工过程来进行计算[2]。SNN使用脉冲(发生在某个时间点的事件的离散值)来传递信息，不仅传递空间信息，还加入了时间信息的传递，计算能力更强。但目前关于SNN的研究刚刚起步，缺乏有效的SNN网络结构和学习算法，严重限制SNN的发展。目前已有的SNN算法有STDP(spike timing dependent plasticity)、ReSuMe(remote supervised method)和SpikeProp等，在现有算法的基础上，本文提出了基于STDP规则的权值学习算法，通过调整引导神经元的激发时间来间接调整目标权值，在网络结构方面，利用生物学的条件反射原理结合Hebb规则提出了脉冲神经网络突触的生长算法，通过该算法可以实现网络的自生长和自适应，同时提出了具有普适性的四层脉冲神经网络结构。为了验证网络结构和算法的可行性，本文将算法应于不完美信息博弈[3]中，扑克游戏是一种典型的不完美信息博弈，本文将会以斗地主扑克游戏为例，通过SNN网络结构和算法来学习一个人的打牌能力，实现一个拟人化的斗地主机器人。

1 脉冲神经网络理论基础

1.1 脉冲神经元模型

传统神经网络的神经元通过乘加运算和激活函数，从数学角度使用“统计+计算”的方式对数据进行处理[4,5]；而脉冲神经元通过复现生物神经元工作状态及状态变化过程，建立具有仿生型的模型，结合神经形态学和神经动力学角度对生物神经元进行模拟。目前广泛认可的脉冲神经元模型[6]有：Integrate-and-fire模型、Hodgkin-Huxley模型、Fractional-Order Leaky integrate-and-fire模型、泄漏积分放电(leaky integrate-and-fire，LIF)模型等。为了同时兼顾模型参数复杂度和生物学仿生精确度，本文采用LIF模型。

LIF神经元等效为一个带有电压源偏置的电阻与电容并联的模型，通过电容的充放电实现改变神经元的膜电位。如果神经元膜电位上升到激活阈值，那么就会导致神经元的激发，从而在输出端产生一个脉冲信号，神经元膜电位会迅速下降到静息电位。

图1为LIF神经元等效电路。

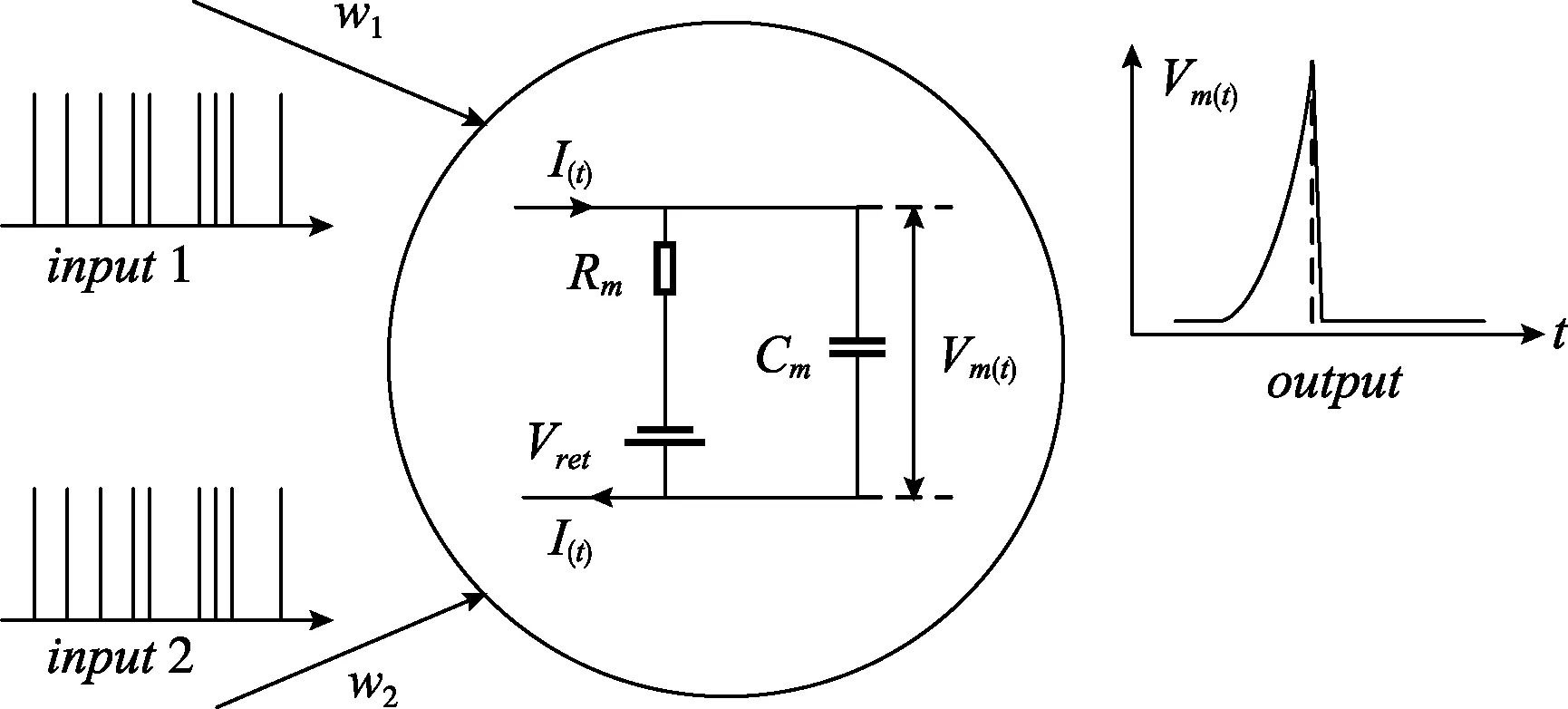
图1 LIF神经元等效电路

根据膜电位的变化，将LIF神经元的活动状态分为3种：电荷泄漏、电荷积累和脉冲发射。且神经元的电荷泄漏和电荷积累过程可以使用数学公式进行表示，如式(1)所示

(1)

其中，Vm(t)，Cm，Rm，I(t)分别为神经元膜电位、膜电容、膜电阻和充电电流；Vret为偏置电压源，为神经元提供静息电位。input1和input2，w1和w2分别为神经元的输入的脉冲信号和对应权值，output输出脉冲信号。

1.2 STDP规则

Spiking-timing-dependent-plasticity(STDP)[7]称为突触可塑性规则，是一种对生物神经元突触变化规律的描述，来源于生物实验的因果学习的规则。图2是算法。

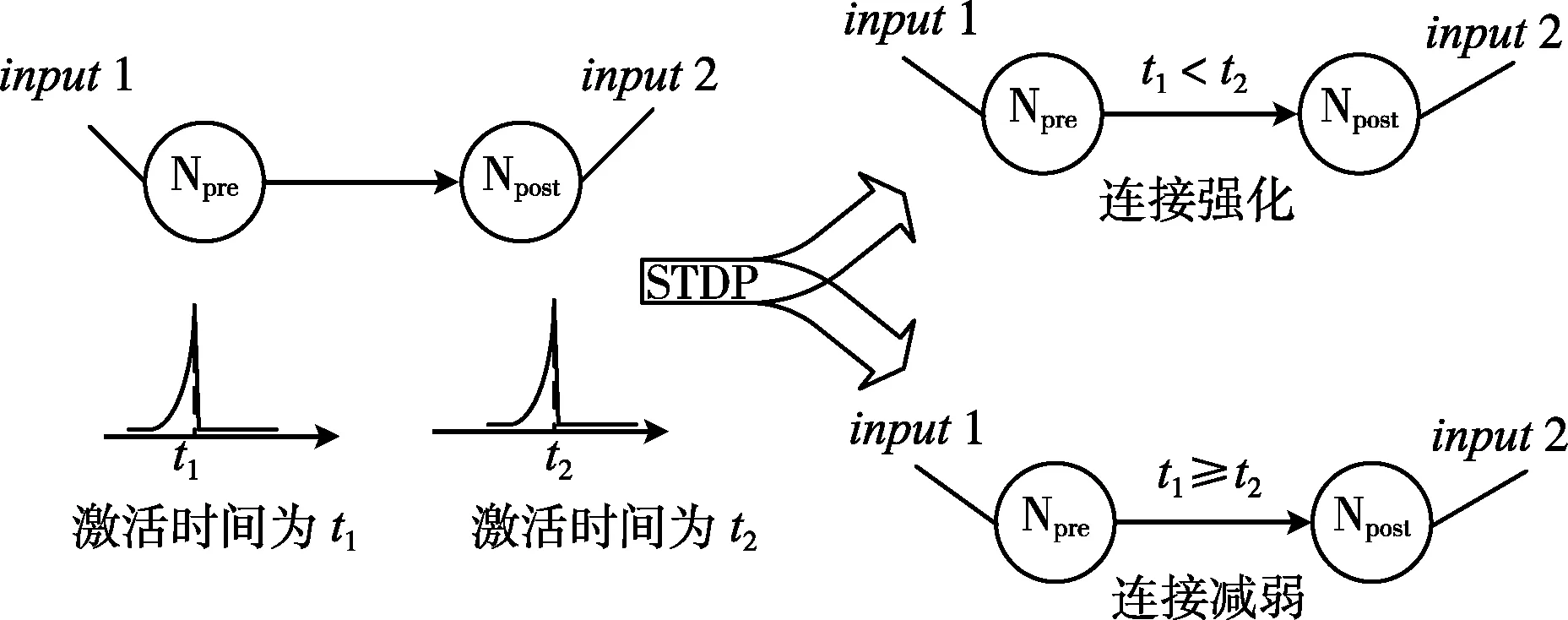
图2 STDP规则

当满足因果关系时，即：突触前神经元(Npre)激活时间早于突触后神经元(Npost)激活时间的时候，增加两个神经元之间的连接权值；反之不满足因果关系时，减弱连接权值。权值变化幅度与连接前后神经元激活时间的函数关系，如式(2)和式(3)所示

Δt=t2-t1

(2)

(3)

其中，t2，t1分别为Npost，Npre激活时间；τ为衰减速率；α为对称度调整参数；μ为控制指数曲率的因子；λ为权值的学习率；w为突触连接权值，如果w取值范围不为区间[0,1]，需要先进行归一化。根据w与t的函数关系，可以得到STDP规则函数曲线，如图3所示。

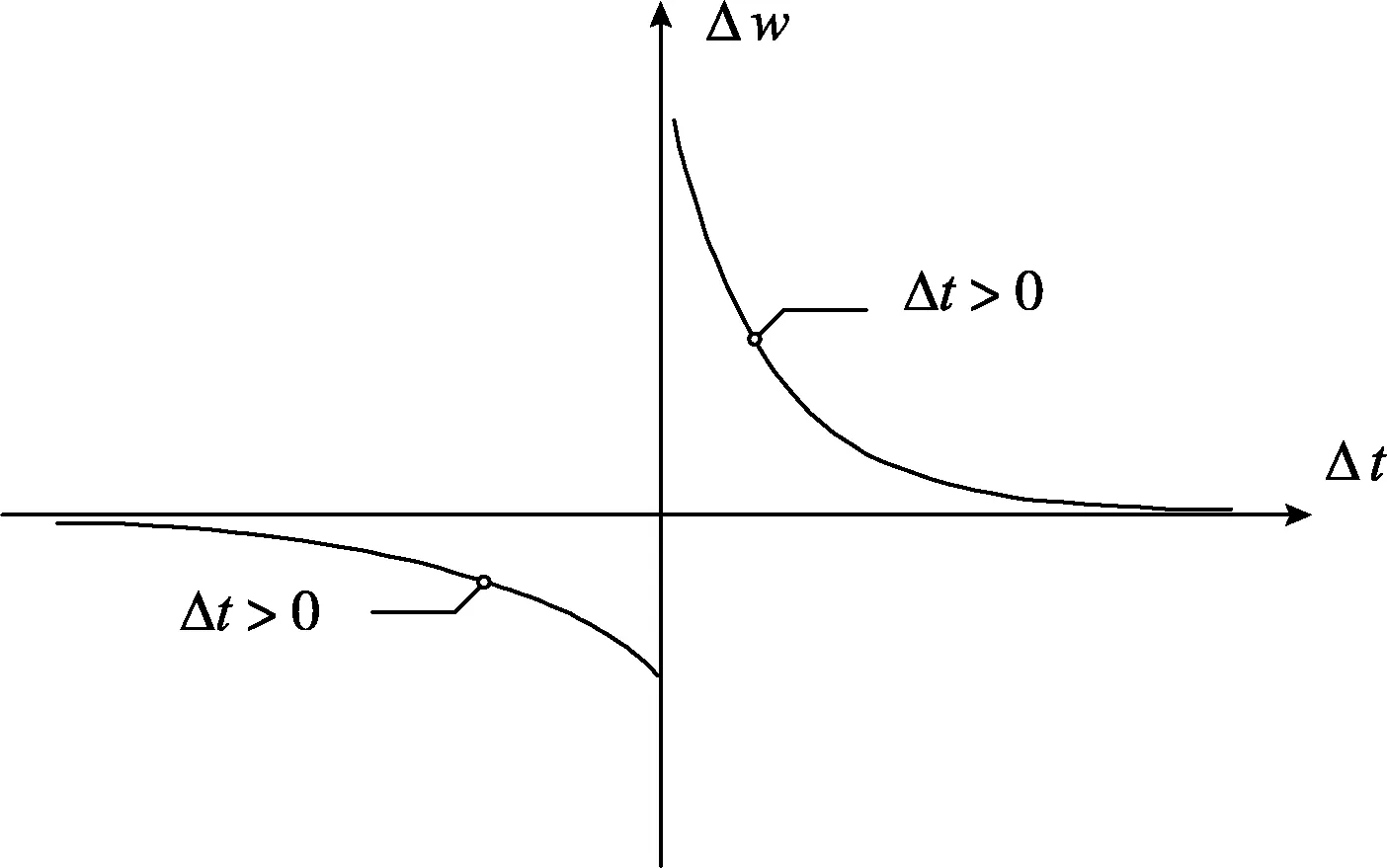
图3 STDP规则函数曲线

2 脉冲神经网络算法

2.1 基于STDP规则的权值学习算法

STDP是基于生物学因果关系的无监督学习[8]，为了设计监督式学习算法，本文参考STDP规则[9]，并对算法进行改进。通过添加一个“引导”神经元，调整激活时间t3，即可改变Npost神经元的激发时间t2，再根据STDP规则，从而达到了间接调整Npre与Npost的权值w1的目标。监督式学习算法实现方式如图4所示。

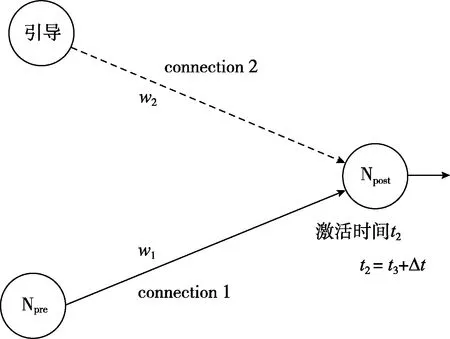
图4 基于STDP规则的权值学习算法

监督式学习算法通过对引导神经元激活时间的控制，能够达到对Npost神经元激活时间的调整，最终实现对connection1的增强或者抑制，图5是权值增强和权值减弱的实验。

首先，进行了权值增强实验，采用引导神经元对两个神经元之间的连接进行权值增强的训练，如图5(a)所示，通过引导神经元对连接后端神经元Npost的作用，能对神经元之间的连接起到明显的增强效果，连接权值w1增长速度随着迭代次数的增加而逐渐趋于稳定。

与权值增强实验类似，采用抑制性引导神经元对两个神经元之间的连接进行权值减弱的训练，如图所示，连接权值w1减弱速度也会随着迭代次数的增加而趋于稳定，如图5(b)所示。

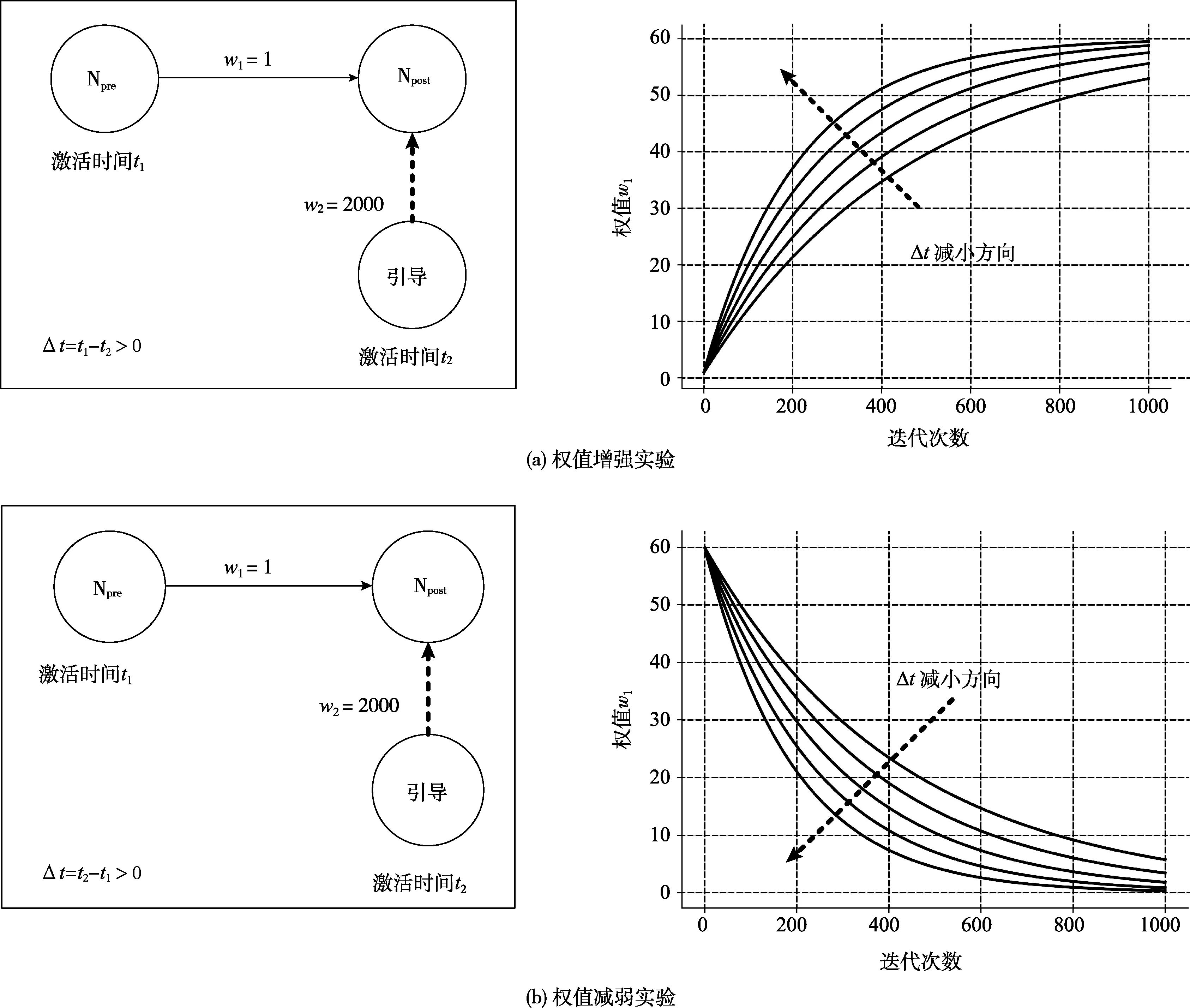
图5 权值增强实验和权值减弱实验

2.2 基于Hebb规则的结构学习算法

文章基于Hebb规则的基本原理[10,11]，提出了基于Hebb规则的神经元连接算法。算法中规定，在同一轮仿真迭代周期内，如果两个神经元的激活时间相近，时间差小于某一阈值，并且两者之间未存在连接，则在这两个神经元中间建立一条连接，连接的方向从先激活的神经元指向后激活的神经元。基于Hebb规则的神经元连接算法，如图6所示。

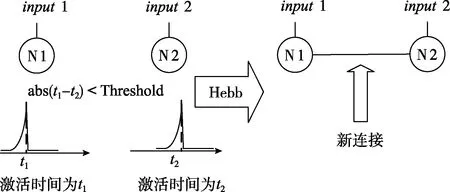
图6 基于Hebb规则的神经元连接

同时，在算法中规定神经元新连接的产生需要考虑位置因素，当两个神经元位置超出距离阈值后，即便神经元活动存在一定的相关性，也不建立连接。而在结构学习算法中，也在网络中添加了神经元的坐标信息，用于衡量神经元之间的位置关系。Hebb规则具体算法流程见表1。

表1 Hebb规则具体算法流程

3 非完美信息博弈——斗地主游戏

目前，人工智能在游戏方面取得了里程碑式的突破[12]，但这些游戏的基本特征是游戏中玩家能够获得完美信息，在非完美信息的应用场景[13]，目前仍是挑战性课题，扑克游戏是典型的非完美信息博弈，本文将以斗地主游戏为例来验证算法的可行性。

不同于传统神经网络，提前考虑了所有可能出现的状态并制定对应策略[14]，本文不是事先制定策略，而是通过根据SNN的特性生成仿生型网络结构，通过SNN算法训练网络权值。在面对博弈时，考虑当前的游戏状态，输入到SNN网络中，再每一步重新计算策略。通过这样的仿生型网络学习一个人的打牌能力，且最终结果是以拟人化程度作为评判网络性能的标准，而非像传统神经网络采用胜率作为评判标准。

为此，本文提出了具有普适性的四层神经网络结构，一种基于脉冲神经网络在非完美信息条件下决策的方法。建立输入层，对非完美信息条件下的信息进行预处理，将输入信息转换为脉冲信号，产生并激发输入层神经元；建立规则层，将所有可能发生的事件划分为样本点，每个样本点对应产生一个规则层神经元，将所有可以激发样本点的输入层神经元与该样本点对应的规则层神经元全连接；建立决策层，在决策层生成神经元，决策层神经元个数和规则层神经元个数相等，将规则层神经元和决策层神经元一一对应，并根据脉冲神经网络算法建立决策层层内连接；建立输出层，根据决策层的网络结构和权值输出信号。如图7所示，这种四层网络结构简单，不涉及大量计算，提高了非完美信息条件下决策的效率且准确度更高。

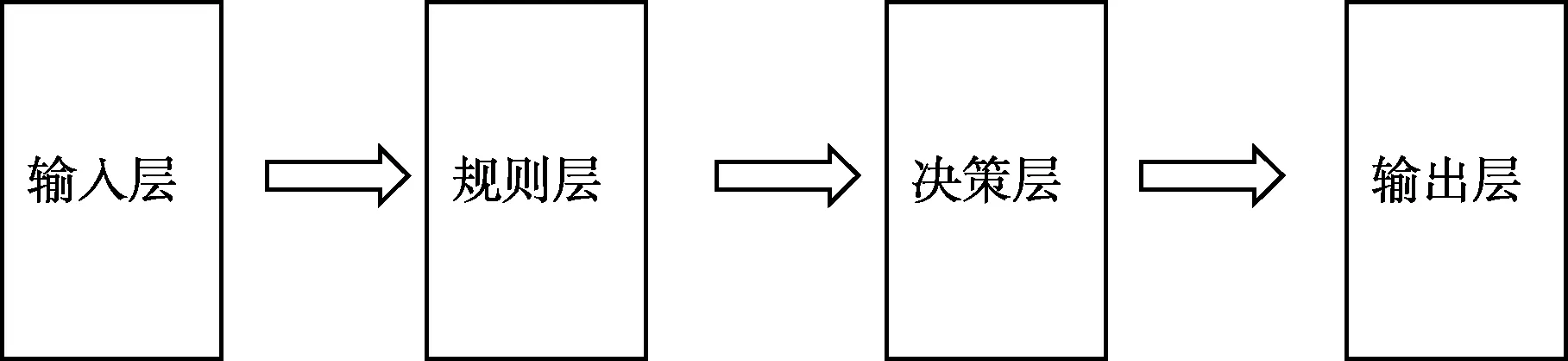
图7 基于非完美信息条件下的四层脉冲神经网络结构

3.1 基于脉冲神经网络的斗地主叫牌

斗地主叫牌输入信息为17张手牌，输出信息为是否叫牌。根据上文提出的普适性四层网络结构，整个叫牌网络分为四层结构，如图8所示。

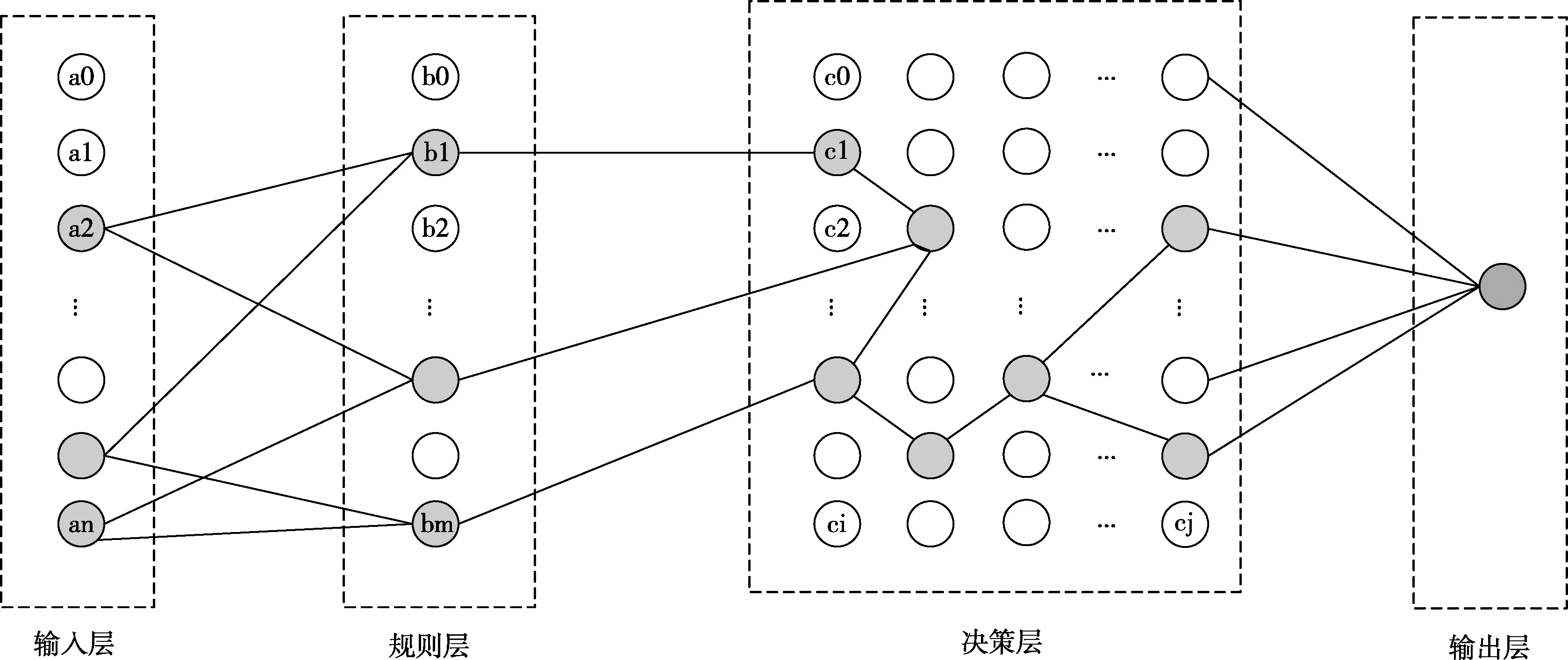
图8 斗地主叫牌的四层网络结构

网络分为4层：

输入层：载入原始数据，并对数据进行预处理，将卡牌转换为脉冲序列。输入层神经元个数54个。将54张牌进行数据处理，根据脉冲转换规则，将每一种牌转换为对应的神经元脉冲发射时间。

规则记忆层：将斗地主里的所有规则进行了定义。单张、双王、炸弹、对子、三张、三带一、三带二、四带一、四带二、三连对、四连对、五连对、六连对、七连对、八连对、九连对、十连对、五张顺子、六张顺子、七张顺子、八张顺子、九张顺子、十张顺子、十一张顺子、十二张顺子、二连飞机、飞机带翅膀、三连飞机、飞机带两对、四连飞机、三连飞机带翅膀、五连飞机、三连飞机带三对、四连飞机带翅膀、六连飞机、四连飞机带四对、五连飞机带翅膀，共277个规则，对应277个神经元，并按照相应的规则连接输入层和规则层。

决策层：也可以称为推理层，对现有的牌进行组合，形成类似生物体的脑结构。在决策层中生成277个神经元，并以二维空间分布。神经元在空间位置分布上按照牌型优先级分布，如图8的layer3所示，优先级是对斗地主规则牌型大小的排序等级。对叫牌贡献大的牌型规则优先级为高，依次至对叫牌贡献最小的牌型规则优先级为低。将规则层神经元和决策层神经元采用“one-to-one”的连接方式。

输出层：一个输出(1/0)。决策层神经元全连接至输出层神经元。

网络形成的决策层类似于生物体的大脑结构，具体决策层的形成方法是在网络训练过程运用基于STDP的权值学习算法和Hebb连接算法调整决策层内部的突触连接关系和权值大小。具体为：在决策层中，运用Hebb规则，获取两个独立神经元的位置，判断两个神经元的相对位置是否小于2，若大于2，神经元之间不建立连接，反之小于2时，获取两个独立神经元的脉冲激发时间，计算激活时间差值是否小于时间阈值(1.0 ms)，若是两个神经元建立连接，并设置其权值为1180.0，反之不建立连接。在时间和空间的连接规则下，形成了决策层的层内连接关系。

通过STDP规则，训练网络的权值大小。在训练过程中，设置决策层中优先级高的神经元连接到输出层神经元的初始权值较大，反之优先级低对应的初始权值较小。根据输出信号即是否叫牌来对决策层到输出层的连接权值进行权值调整，若此轮训练过程中叫牌，则增加引导神经元至输出神经元的连接权值，根据本文改进的STDP规则，会增大决策层内神经元至输出神经元的连接权值；不叫牌则反之减小权值，权值调节的大小如式(2)、式(3)所示。训练完成后形成的网络即可以实现斗地主叫牌功能。表2为斗地主叫牌算法流程。

表2 斗地主叫牌算法训练流程

3.2 基于脉冲神经网络的斗地主出牌

斗地主出牌相对于斗地主叫牌有更多的不确定性因素。根据游戏规则，玩家出牌有两方面的影响：一是玩家手中的牌；二是上家的出牌情况。上文提出的普适性的脉冲神经网络的四层网络结构同样适用于斗地主出牌阶段，图9是基于四层脉冲神经网络设计的斗地主出牌框架。

输入层：斗地主出牌受两方面的影响，一是玩家手中的牌；二是上家的出牌情况。所以输入层有两个，为了方便区分，我们将上图的网络分为本家出牌网络，其输入信号是玩家手牌信息，以及上家网络，其输入信号是上家的出牌。

规则层：将斗地主里的所有规则进行了定义。单张、双王、炸弹、对子、三张、三带一、三带二、四带一、四带二、三连对、四连对、五连对、六连对、七连对、八连对、九连对、十连对、五张顺子、六张顺子、七张顺子、八张顺子、九张顺子、十张顺子、十一张顺子、十二张顺子、二连飞机、飞机带翅膀、三连飞机、飞机带两对、四连飞机、三连飞机带翅膀、五连飞机、三连飞机带三对、四连飞机带翅膀、六连飞机、四连飞机带四对、五连飞机带翅膀，共277个规则。本家出牌网络和上家网络的规则层分别对应各自的规则层，如图9所示。且由于本家出牌时，要考虑不同情况将本家的规则层layer2分为3个通道，不同的游戏场景下激活相应通道的规则层，3种场景分别是：

其次是或将影响行业复苏。在集运市场，班轮公司在经过整合后对投放市场的运力达成更多共识，一直偏离价值的运价也终将向正常范围靠近。如果中美贸易战全面升级，美国将征收关税对象的产品清单向低附加值货物扩展，将给班轮公司带来运量和运价的双重压力，这将打破集运市场周期复苏的势头。随着下降趋势持续推进，将从集运市场波及散运以及油运市场，从而进一步影响整个航运市场。

(1)本轮游戏，本家玩家主动出牌，没有上家出牌。

(2)本轮游戏中，本家属于跟牌，且出牌的上家是敌方。

(3)本轮游戏中，本家属于跟牌，且出牌的上家是友方。

决策层：将符合上家出牌规则的本家网络layer2中的神经元输出至决策层。

输出层：输出出牌结果。

其中输入层和输出层的处理比较简单，不做介绍，将主要介绍规则层和决策层。

3.2.1 斗地主出牌网络的规则层

斗地主的出牌规则层是对输入数据规则的判定，由于输入层分为了本家和上家两个输入模块，所以对于规则层也需要两个规则层模块分别对两个输入进行规则的划分判定，如图9所示。

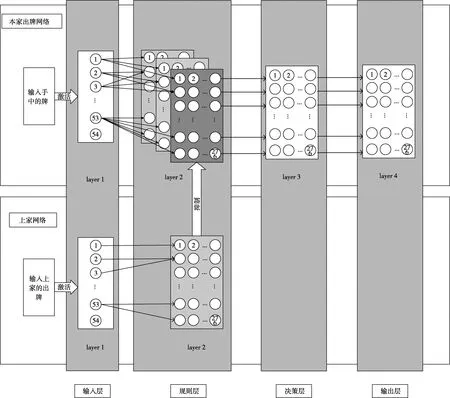
图9 基于脉冲神经网络的斗地主出牌框架

对上家网络的分析，根据规则层判断出上家出牌的大类规则即可，所以上家网络规则层与叫牌阶段的规则层分析及规则的划分一致。

(2)本家网络的规则层

由于本家网络在出牌的时候，针对不同的情况有不同的处理方法，本文对情景进行划分，分为以下3种场景：本轮游戏，本家玩家主动出牌，没有上家出牌；本轮游戏中，本家属于被动跟牌，且出牌的上家是敌方；本轮游戏中，本家属于被动跟牌，且出牌的上家是友方。

对于以上的3张出牌情况将本家网络的规则层分成3个通道，每一种通道对应一种出牌情况，输入层与每一个通道的规则的连接关系与叫牌阶段的一致，即每一个通道都与本家网络的输入层建立连接关系，输入层至规则层的连接情况和权值与斗地主叫牌时的连接一致。3个通道分别代表的是3种场景，所以规则层的不同通道的神经元不建立连接关系。

且本家出牌的规则层受到上家出牌规则的限制，所以本家的layer2激发情况受到上家网络layer2的限制，只有和其规则保持一致，且牌型比上家的大的神经元才能被激发传递到下一层网络。

3.2.2 斗地主出牌网络的决策层

本家规则层的3个通道分别与决策层连接，连接方式为“one-to-one”的形式，初始状态决策层内部无连接关系，通过脉冲神经网络的学习算法，在决策层内部生长出新的突触，形成类似生物体的脑结构。通过生成的决策网络学习输入数据的出牌能力。在决策层中生成277个神经元，并以二维空间分布，神经元在空间位置分布上按照牌型优先级分布，优先级是对斗地主规则牌型大小的排序等级。对叫牌贡献大的牌型规则优先级为高，依次至对叫牌贡献最小的牌型规则优先级为低，和叫牌的决策层的优先级分布一致。

通过网络的结构和权值训练形成类脑的出牌决策层。

训练的过程是：初始化出牌网络结构。输入玩家的手牌和上家的出牌情况，将信号依次输入至规则层，然后至决策层，在决策层内部根据Hebb生长算法，生成决策层内部的突触连接，根据Hebb的突触修正公式调整决策层内部的连接权值。再通过STDP规则，训练决策层至输出层网络的权值大小。在训练过程中，设置决策层中优先级高的神经元连接到输出层神经元的初始权值较大，反之优先级低对应的初始权值较小。根据输出信号即数据集的出牌神经元id找到其对决策层的神经元，增大该神经元至输出层的连接权值，减小与其它决策层神经元的连接权值。训练完成后形成的网络即可以实现斗地主出牌功能。

4 斗地主实验结果

4.1 斗地主叫牌实验结果

在斗地主实验中，我们以生成决策层的层内连接及调整决策层到输出层的连接权值为主要目标，通过斗地主叫牌网络实现对一个人叫牌能力的学习。

实验采用的是一名真人的叫牌数据，共计1700组叫牌数据，将其中1500组数据作为训练集数据，200组数据作为测试集。实验以拟人化程度作为评判标准，如式(4)所示

(4)

图10是训练生成的决策网络，决策层最初没有内部连接。在图中，当训练集为10、100和1500时，分别获得决策层中的连接关系。可以看出，在Hebb规则的作用下，连接的数量正在增加，体现出了决策层的学习过程，其中每个网格点代表一个神经元。

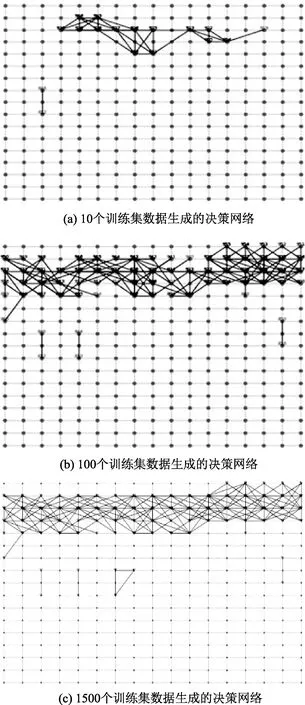
图10 训练生成的叫牌决策网络

可以看到，决策层的层内连接主要在网络的上方部分，即网络优先级高的神经元建立的内部连接较多，对叫牌贡献大。优先级低的神经元极少建立内部连接，对叫牌贡献小。与理论分析一致。

我们以一组数据为例，对实验进行测试模拟。测试集为2KKKKJJJJ55553333。

图11为输入层神经元的整体激发情况，输入层对输入数据进行预处理并将输入数据转换为脉冲信号，从图中可以看到此轮游戏中，输入层神经元膜电位随时间的变化曲线，统计膜电位超过阈值电压的神经元id，得到输入层被激发的神经元id。

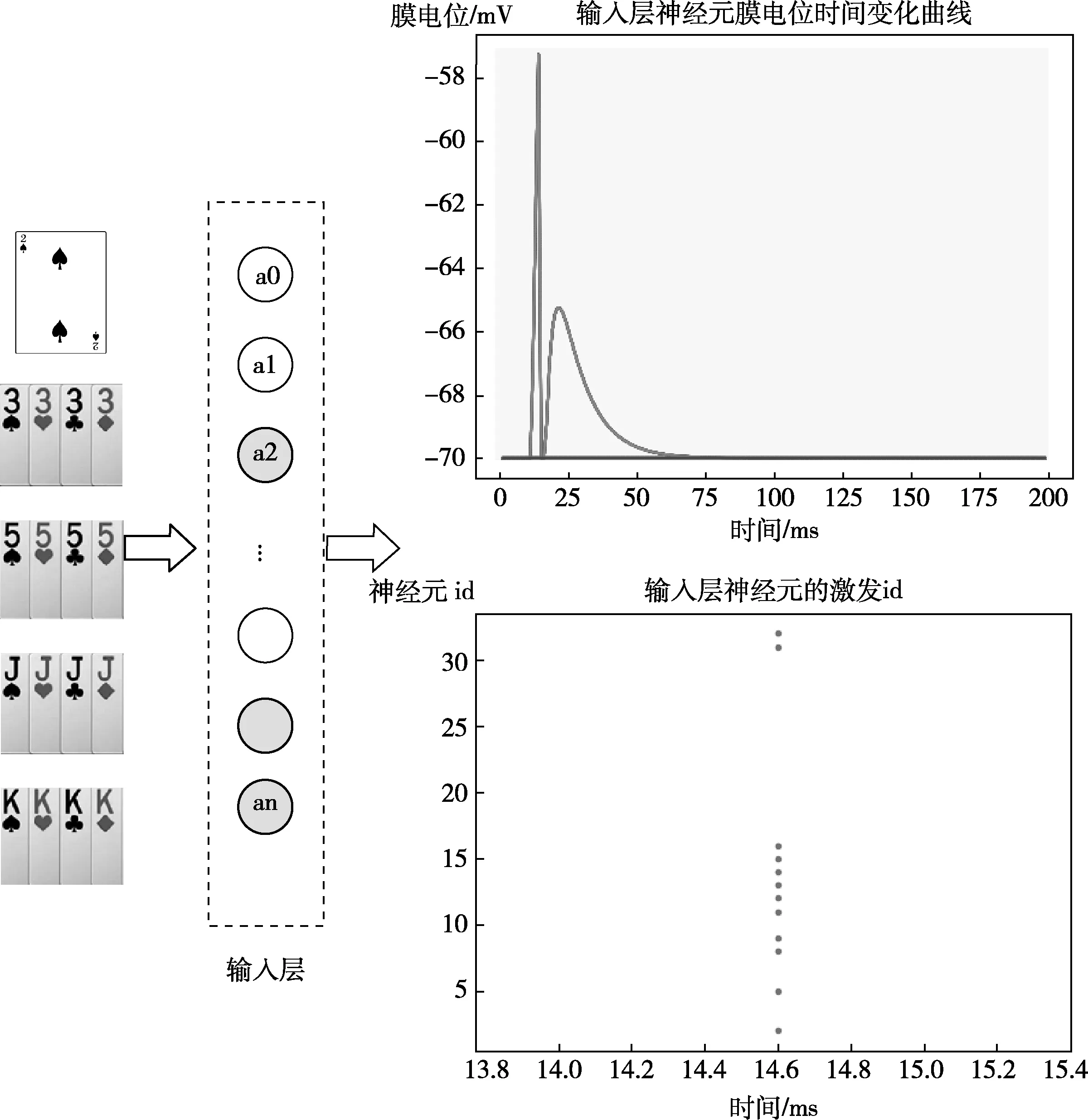
图11 输入层神经元的整体激发情况

通过斗地主叫牌网络，脉冲信号依次被传入规则层、决策层和输出层。

脉冲信号被传入规则层，规则层神经元的激活情况如图12所示，规则层神经元的膜电位随时间的变化曲线如图12(a)所示，规则层被激发的神经元id如图12(b)所示，通过激发神经元的id可以得到在此次游戏中被激发的规则有3，33，333，3333，5，55，555，5555，J，JJ，JJJ，JJJJ，K，KK，KKK，KKKK，2，此轮规则层共13个神经元被激发。

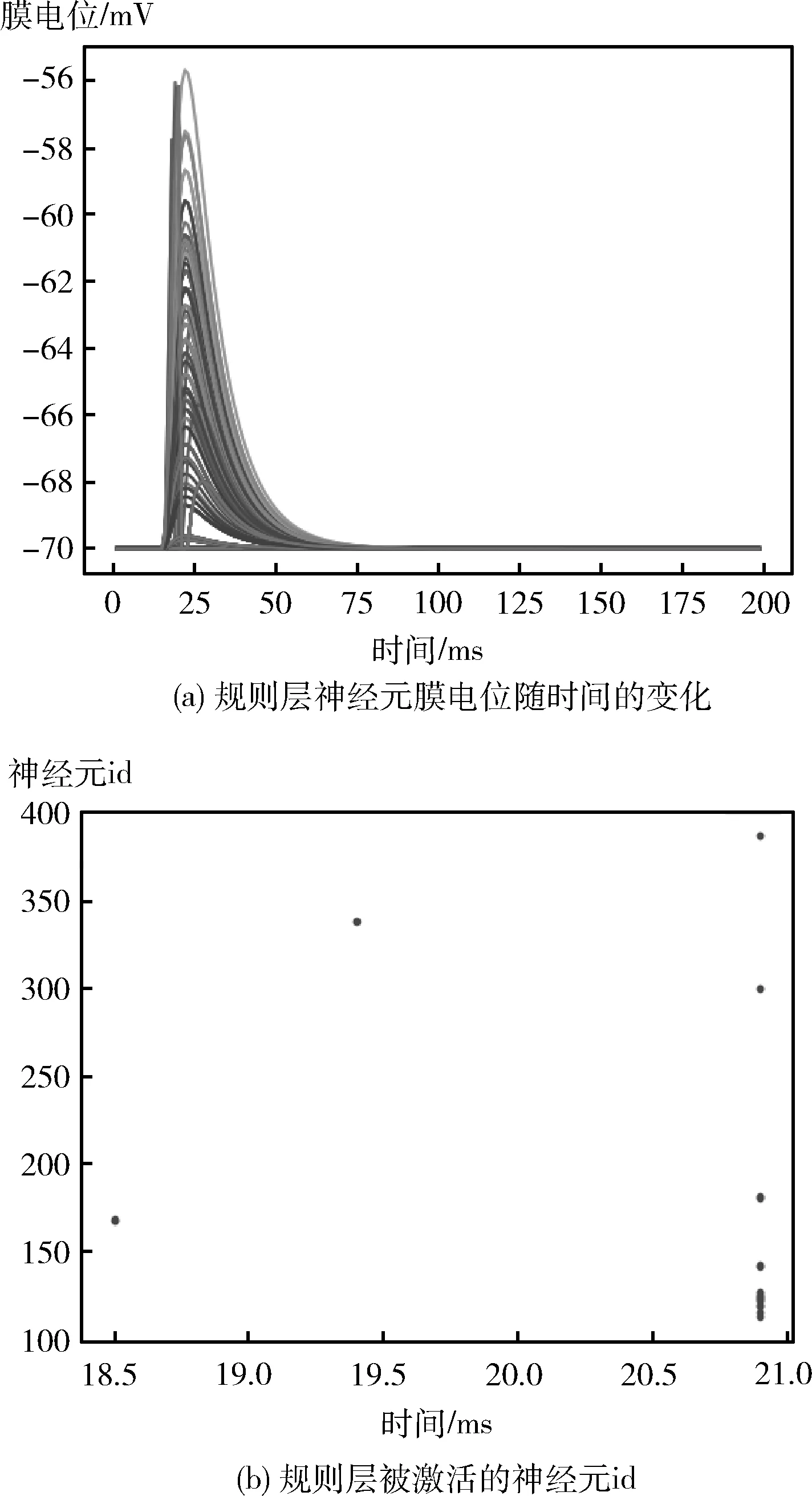
图12 规则层神经元的激活情况

通过图10中的决策层网络，输出层神经元被激发，即该轮游戏中，斗地主机器人输出是叫牌，和测试集数据一致。

通过200个测试数据的测试，测试过程见表3。

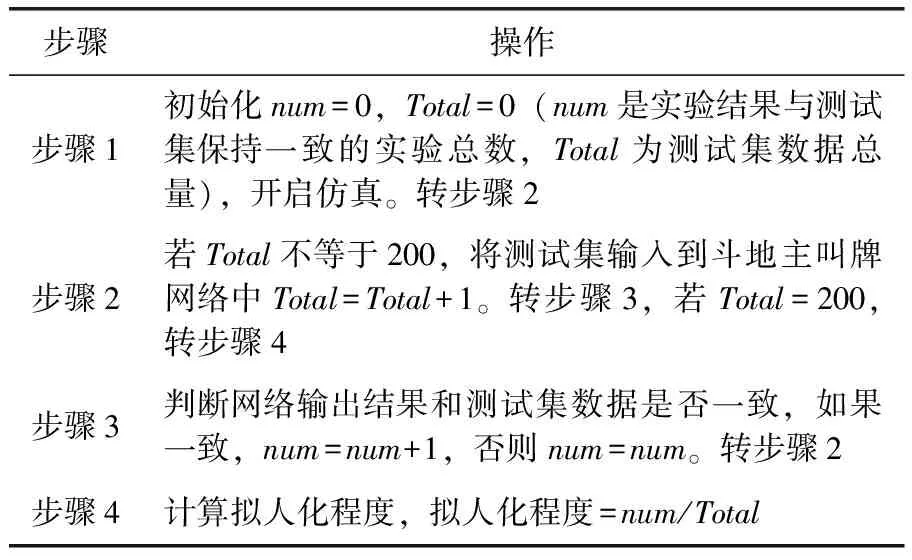
表3 斗地主测试算法

最终得到拟人化程度为85%，实验结果见表4。

表4 斗地主叫牌实验数据

4.2 斗地主出牌实验结果

出牌阶段主要以训练玩家本家网络的决策层内部突触连接和训练连接权值为主，以及训练决策层与输出层的连接权值。通过网络的自生长和自适应算法生成一个可以学习人类打牌的智能体。随着输入数据的训练量增大，决策层内部建立的连接关系变多。图13是对网络进行2500组出牌数据训练得到的网络结构。

图13 出牌决策层网络结构

斗地主出牌测试阶段，网络出牌不具有唯一性，由于网络会对过去已知知识进行学习，所以，会随着输入数据量的增大而发生动态变化。因此出牌的测试仅进行功能性测试，没有量化指标。

以一组数据为例进行功能验证。以此轮游戏玩家主动出牌，且以手牌为4 5 5 6 6 6 7 10 J K A 2 小王 大王为例，没有上家出牌。得到的规则层神经元的膜电位随时间的变化情况如图14所示。将规则层中被激发的神经元将信息传递到决策网络，最终得到的输出结果如图15所示。可以看到输出层的227个神经元仅有一个神经元被激发，且该神经元的id代表的信息是输出结果是4，出牌网络的功能性正常。

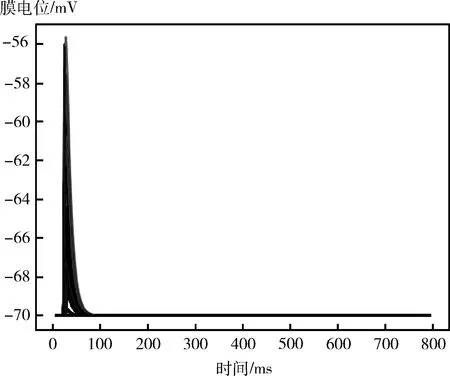
图14 出牌规则层神经元的膜电位随时间的变化

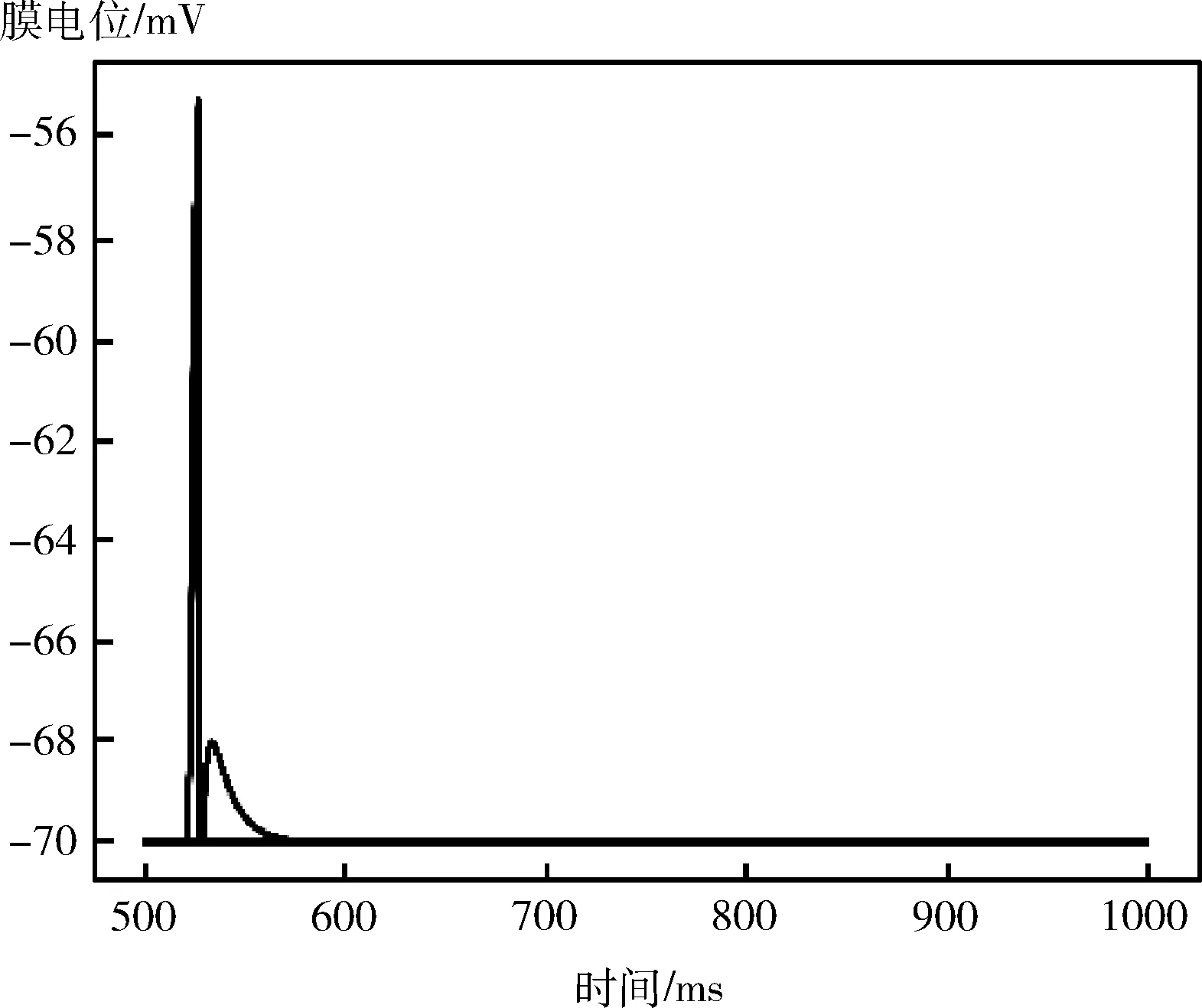
图15 输出层的神经元激发情况

与传统神经网络进行对比，不同于传统神经网络，提前考虑了所有可能出现的状态并制定对应策略，本文不是事先制定策略，而是通过根据SNN的特性生成仿生型网络结构，通过SNN算法训练网络权值。在面对博弈时，考虑当前的游戏状态，输入到SNN网络中，再每一步重新计算策略。传统AI通过所有的牌型评分，每一种牌型都有其对应的出牌结果，选择最优结果，是确定性的数据分析和运算，不具备智能性。而SNN网络的斗地主：通过形成类似人脑结构的决策层网络，建立网络内部的连接关系和权值，具有动态学习能力，且智能程度很高。

5 结束语

综上，创新性点在于提出了一种基于STDP规则的权值学习算法和基于Hebb规则的结构学习算法，这些算法解决了目前脉冲神经网络的学习算法的不完备性。结合SNN特性，将算法引入不完美信息博弈中，以斗地主扑克游戏为例，实现了一个拟人化的斗地主机器人，该机器人相对于传统AI，更加的智能，并非事先制定策略，而是学习一个人的斗地主能力，生成叫牌决策网络，最终的拟人程度为85%，在出牌网络中，训练出的网络的功能性是正常的，下一步工作会在当前算法的基础上，加入增强学习的算法，继续完善斗地主叫牌和出牌网络，使得其智能化程度更高。