一种基于矩阵优化的高效频繁项集挖掘算法
陈万敏
中国人民银行兰州中心支行 甘肃 兰州 730000
引言
数据挖掘是从实际应用产生的数据中,发现隐含在其中且人们之前未掌握的、但对社会和行业发展有价值的信息和知识的过程。通常这些数据有规模庞大、种类繁多、增长速度快等特点[1]。关联规则对发现大数据之间的隐藏信息具有重要意义,可以视为数据挖掘的重点研究对象之一。为了探索大数据内隐含的信息,Agrawal等[2]首次提出关联规则算法Apriori,该算法的基本思想是对数据库进行重复扫描[3],依据反单调性将给定的维生成所需要的k维频繁项集。首先需要找到频繁项中的项集L1,通过L1挖掘L2,L2挖掘L3,逐层进行挖掘,直到挖掘不到更为频繁的k项集,每次只能找到一个Li,下一频次挖掘须再次扫描数据库。Apriori算法虽实现了较好的效果,但存在一些问题:一是该算法会对数据库进行多次扫描,候选项集中的每项都需要扫描一次数据库,以判定是否可以加入频繁项集,导致输入/输出的负担过重;二是由于会产生大量的频繁项集候选项,因此要耗费大量主存空间和相应的计算时间。针对此问题,本文提出了一种基于矩阵优化的高效频繁项挖掘算法(Matrix Weight Sort Apriori,MWS_Apriori)。该算法对数据库仅扫描一次,将事务数据转换为0-1事务矩阵形式,并且会对频繁项集的项赋予相应的权重,使用基数排序对频繁项集重新排序,减少判断的次数,以此来降低产生候选项集时所需的计算量。该算法能够相对有效地减轻I/O负担,并减少运算次数,不仅能有效提高内存利用率,且在一定程度上能大大缩短规则产生的时间。
1 Apriori算法的相关研究
Apriori算法原理是利用逐层搜索的方式来寻找相应的频繁项集,主要步骤为:第一步将k项集自连接生成项集,第二步将不满足最小支持度的项进行剪枝。Yu等[4]使用带标签的算法,减少了针对候选2项集进行冗余修剪的操作;Bhandari等[5]将聚类和并行算法进行结合,减少对存储空间的需求,相比之下,该方法在生成候选支持度时,时间消耗减少了67.87%;Bera等[6]以较小的空间作为代价提出一种随机算法技术,该技术尽可能多地输出频繁项集,并降低时间开销。Vaithiyanathan等基于压缩数据库的想法提出了一种改进的先验算法,并通过实验证明了该技术的有用性;Slimani等采用一种二进制数据集结构,将三个数据集用于算法进行比较;Yu等根据哈希表可快速进行查找,提出了一种基于前缀项集的候选存储结构的办法,能极大限度地提高传统算法在进行连接、剪枝中的效率,当支持度的数值越小时所提升的效率越大。
2 MWS_Apriori算法
2.1 MWS_Apriori算法
MWS_Apriori算法思路如下:
2.1.1 扫描源数据,以项为行,事务为列,转化生成事务矩阵,矩阵W中的值初始化为1。
2.1.2 若矩阵中有相同的事务,则该列在W中对应的值加1,删除重复的事务列。矩阵N为每项对应的行按位与W中的值相乘的和,即项的支持度计数。矩阵M为每个事务所包含的项数。若N中的值小于min_sup,则将该元素在矩阵中所在的行进行删除,余下的即为频繁项集。更新矩阵M,当矩阵M中某个元素值为0时,将该元素所在的列进行删除,由此得到矩阵D1。
2.1.3 将所有频繁1-项集对应的行进行两两结合并进行对应项的逻辑与操作,生成2-事务矩阵,重新计算并生成矩阵N,删除N中值小于min_sup的元素在矩阵中对应的行,重新计算矩阵M,若M中的某值小于2,则删除该元素在矩阵中对应的列,得到压缩后的矩阵D2。
2.1.4 对频繁项集中单项所出现次数进行统计,根据统计的结果按照基数排序法中的递增顺序将频繁项集进行重新排序。
2.1.5 依据(k -1)-候选项,将所有(k-1)-项频繁项集中满足前(k-2)个项相同的行进行两两结合,并将结合后所得的项与对应项进行逻辑与操作,重新计算并生成矩阵N,删除N中值小于min_sup的元素在矩阵中对应的行,重新计算矩阵M,若M中的某值小于k,则将该元素所对应的整列进行删除,即对矩阵进行压缩,压缩后所得矩阵Dk(k≥3)。
2.1.6 对于压缩后的矩阵Dk(k≥3),包含的是对应的k-项频繁项集,其相对应的矩阵N保存了每一项频繁项集的支持度计数。
2.1.7 判断频繁项k-集的个数是否小于k+1或生成频繁项目的集合是否为空,若是则停止搜索;反之,则重复步骤(5)~(7)。
2.2 MWS_Apriori算法的实现
本文从两个方面对Apriori算法进行优化改进:一是转换成0-1事务矩阵;二是对频繁项集的项排序,对满足前(k-2)个项相同的项进行连接。该算法的具体实现过程如下:
2.2.1 对事务数据库进行扫描,从而生成0-1矩阵D及矩阵W。事务T3和T6、T5和T7含有相同项目,所以第3、5列的权值设置为2,其余的权值均为1。
2.2.2 1-项频繁项集,第一步对矩阵D中列元素为1进行逐个累加求和得到矩阵M。第二步删除M中数值≤1所对应的列,将矩阵D中每行与所对应的权值进行相乘,将相乘之后每行的数值进行相加并按行拼接在一起形成矩阵N。第三步假设Ii=[1001111],通过support_count(Ii)=Ii×WT=6得到其他项的支持度计数,删除N中≤min_sup的行,重新计算得到M,直到矩阵无变化为止。由此可得I1,I2,I3,I4,I5,为1-频繁项集。
2.2.3 2-项频繁项集,第一步将所有1-频繁项集中每行进行求与运算形成矩阵D1。第二步将列中数值为1的元素进行累加得到矩阵M。第三步对每行的项集求支持度得到矩阵N。第四步将M中数值≤1的所对应的列删除,将N中数值≤min_sup的所对应的行删除,直到矩阵无任何变化,得到矩阵D2。
2.2.4 3-项频繁项集,第一步将2-项频繁项集中的各项,按照单项出现的次数进行递增排序。第二步将排序后的2-项频繁项集中满足条件的项集两两结合,进行对应项的逻辑与操作后生成矩阵。第三步将列中所有数值为1的元素累加得到矩阵M。第四步对每行的项集求支持度得到矩阵N。第五步将M中数值≤1的列删除,把N中≤min_sup所对应的行删除,直到矩阵无变化为止,得到矩阵D3。
2.2.5 3-项频繁项集的个数求解为2,小于4,则终止求4-项频繁项集,那么最大频繁项集为频繁3项集,结束算法。其中,D={T1,T2…T9}表示数据库中存有9个事务;I={I1,I2,I3,I4,I5}表示对应的项目集;min_sup=2。
MWS_Apriori算法能在扫描次数最少的前提下,减少候选项集的冗余项,提升算法执行效率。
3 实验及算法性能分析
3.1 实验平台与数据集
为了验证本文改进MWS_Apriori算法的有效性和高效性,对Apriori、FP-Growth和MWS_Apriori算法在4个公共数据集上进行对比实验,并根据试验结果进行统计分析。
3.2 运行时间比较分析
为验证在不同最小支持度和不同事务数量情况下算法的执行时间,本文采用了多次取平均的方式消除多次实验带来误差的影响,并将以上3种算法在4个数据集上的不同最小支持度执行时间做了对比。通过结果对比可以发现,MWS_Apriori算法在效率上好于其他的算法,并且随着最小支持度增加,3种算法运行时间都呈下降的趋势。从musroom和connect这两个数据集中挖掘出频繁项集的数量远远超过所挖掘的事务数量,因此比较耗时,3种算法的运行时间都随最小支持度增加而趋于平缓,3种算法在处理accidents和T10I4D100K数据集时,运算时间下降幅度都较大。
图1显示了包含MWS_Apriori算法在内的3种算法在4种不同公共数据集上的具体表现,可以看出当每个数据集所持有的支持度相同,事务的数量不同时,3种算法的运行时间都随着事务的数量增加而增加,但MWS_Apriori算法在效率上优于剩下的两种算法。在数据集T10I4D100K中,FP-Growth算法的运行时间随着事务数量增加逐渐接近Apriori算法所用的时间。从上述结果可以看出,改进之后的MWS_Apriori算法运行时间的波动幅度明显小于其他两种算法,并且随着测试数据集的增加,时间幅度波动会越发的稳定,表明MWS_Apriori算法相较于对比算法Apriori算法和FP-Growth算法更加具有鲁棒性。
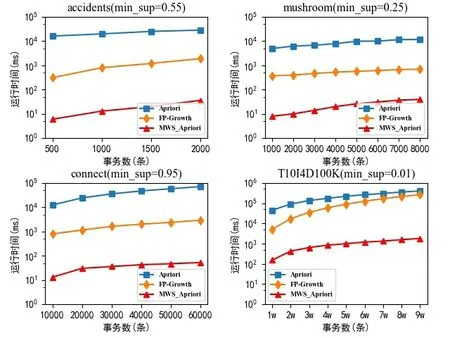
图1 不同事务数的运行效率对比图
4 结束语
本文针对Apriori算法的频繁扫描数据库和产生候选集效率低等问题,结合前人的研究,提出了一种新的改进算法,该算法对事件数据库仅扫描一次,将事务数据库转换为二进制数据中显示的事务矩阵,并挖掘矩阵库,同时依据同一事务出现的次数来赋予权重后根据基数排序法进行重新排序,能减少冗余的候选项集及内存的消耗,实验表明基于矩阵的MWS_Apriori算法的挖掘时间效率较高,算法更具鲁棒性。

