出版社图书印制策略
李柄欣
中央民族大学理学院 北京 100081
引言
对A类书籍进行研究,利用已有数据对A类图书各年报单情况、各年首次报单情况以及各年销售率进行数据拟合得到变化趋势,使用回归模型预测下一年报单、首单情况以及销售率。再由预测所得确定需重印数量,运用0-1数学规划模型讨论重印次数及各次印刷数[1]。
根据已有数据得到B类各图书定价及销售量范围,寻找规律发现定价会影响销售量的变化从而影响利润回报。结合可接受销售率区间得出下一年每本书的印刷量范围,最后运用多目标规划模型[2]讨论得出在降低库存的前提下,出版社获利最多的最优印刷方案。
C类图书定位于长销,销售时间可延续。据已有数据,运用GM灰色预测模型分析图书年销量随时间的变化趋势来近似C类图书的需求变化。
1 模型分析与建立
1.1 回归模型
所有直线中取误差平方和S最小的一条为回归直线,即回归直线的系数a及常数b使S达到极小值。
根据极值原理,要使S达到极小值,式中分别对 a、b 求偏微分,令它们等于 0,于是 a、b满足[1]:

观察上式可知,计算a、b所需的量都可以从观测数据中得到,则回归直线方程y=ax+b便可以确定。
1.2 0-1数学规划模型
数学规划模型的一般形式为:
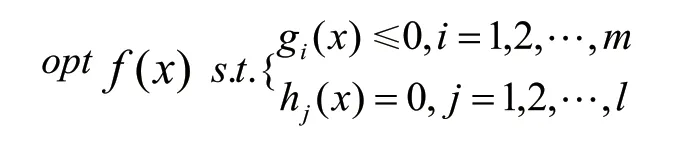
线性规划的一般模型为:
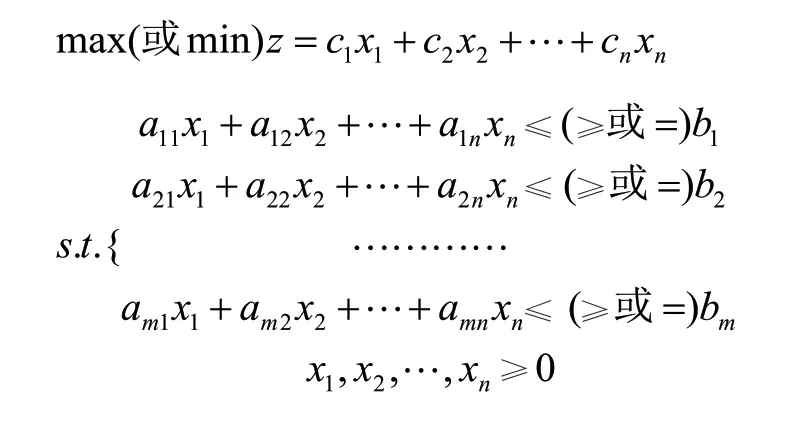
如果线性规划模型中目标函数是非线性的或者约束条件有非线性约束,则上述模型就成为非线性规划模型。
1.3 多目标规划模型
多目标规划模型是在0-1规划模型的建立过程中多了一个目标函数。多目标规划的处理方法:将多个目标化成单目标优化[3]。

1.4 GM灰色预测模型
灰色预测模型是利用离散随机数变为随机性被显著削弱而且较有规律的生成数,建立起的微分方程形式的模型。

2 模型求解
2.1 问题一求解
目标函数:利润=定价×印数×销售折扣×销售率-(印刷成本+库房发货费)。
根据数据得出A1~A5各种图书报单数量的变化趋势,以及第一次报单数量的变化趋势,使用回归模型预测新一年报单数量以及第一次报单的数量。我们得到5种图书剩余应印刷的数量。表1为A1~A5各图书新的一年印刷次数与印刷量的最优解。

表1 印刷次数与印刷量的最优解
库房发货费用=发货数量×定价×发货费率。发货费率为一定值的2.73%。发货数量已由表1给出,A1~A5的图书定价在附件中已经给出。
综上讨论,A类各图书的利润:
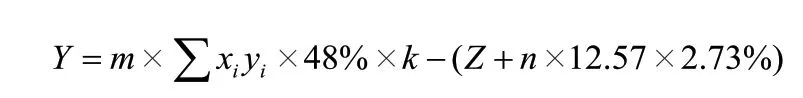
2.2 问题二求解
使用LINGO对模型求解,代入得到B类图书印刷次数与最优解如表2。
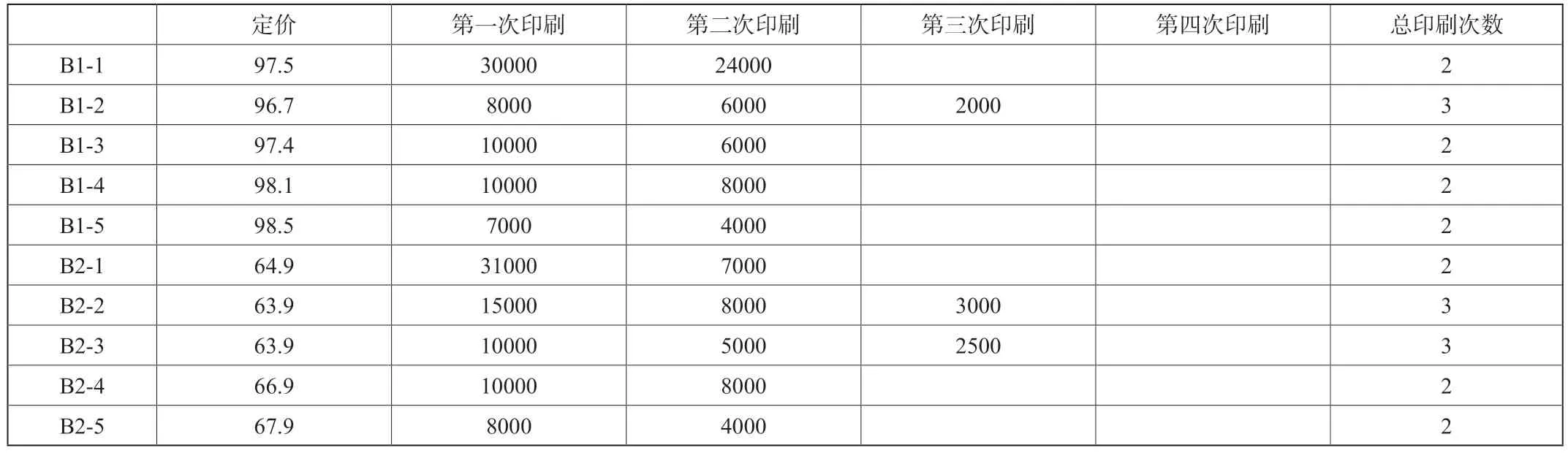
表2 印刷次数与印刷量的最优解
2.3 问题三求解
用MATLAB对C类各种图书的各个季度的销量随时间变化的关系进行绘图,并使用函数拟合已有数据的变化趋势,预测得到之后两年的预测销量变化。C类图书定价不变,可以根据其销量变化作为它的需求趋势,直接用灰度模型预测其销量,得到C类图书这两年内是否需要重印以及需要重印的数量。
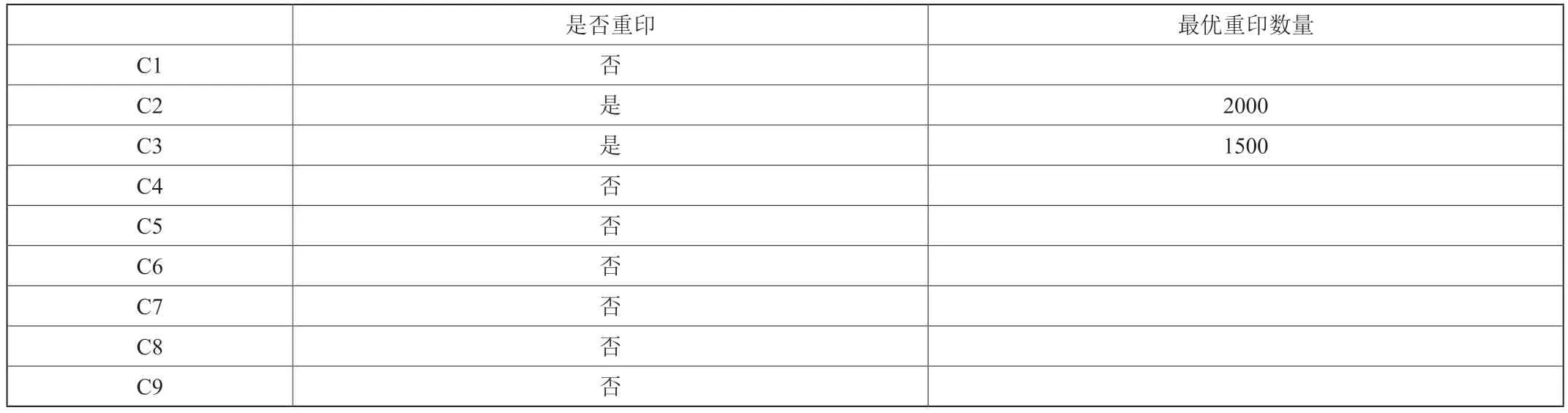
表3 印刷方案
上表给出的是将来两年内出版社的印刷方案。由于题目中说明C类图书上市2年以后,热度就会减弱,我们默认C类图书都是衰减趋势。
C1的重印策略不是最优的,库存量过多。C2的重印策略非最优方案,第二次印刷量减少。C3的重印策略是最优的。C4的重印策略是最优的。C5的重印策略是最优的。C6的重印策略不是最佳的。C7的重印策略不是最优的。C8的重印策略不是最优的。C9的重印策略不是最优的。

