非饱和裂隙膨胀土边坡降雨入渗和变形的数值模拟

程世涛 张维 任鹏

【摘要】裂隙是膨胀土的基本特性之一，它的存在直接影响着降雨作用下膨胀土边坡内的含水量、孔压和变形的发展。文章在已有研究的基础上，给出了膨胀土裂隙模拟的方法及裂隙膨胀土边坡的非饱和渗流过程的模拟方法;建立了一个工程实用的膨胀土的胀缩变形计算模型;发展了适用于裂隙膨胀土边坡的雨水入渗过程分析的数值计算方法，编制了相应程序。结合工程实例，模拟了降雨入渗条件下裂隙膨胀土边坡的含水量、孔压和变形演化过程。数值计算结果较好地再现了现场试验结果，初步说明了模拟方法及程序的可靠性。模拟结果表明，在降雨初期，裂隙发育的浅层土体含水量迅速增加，部分区域饱和;延长降雨后，坡面和坡脚形成略深于裂隙发育区的浅层饱和区;裂隙的闭合导致含水量增加减缓，雨水入渗集中在浅层;在延长降雨后饱和区的扩散仍集中在坡面坡脚的浅层土体。裂隙膨胀土边坡的膨胀和软化也集中发生在浅层土体中，这决定了裂隙膨胀土边坡的破坏形式主要为浅表型滑坡。

【关键词】膨胀土边坡; 裂隙; 降雨入渗; 胀缩变形; 数值模拟

【中国分类号】P642.11+4【文献标志码】A

膨胀土边坡失稳是膨胀土地区的一种非常典型的地质灾害问题。降雨及其导致的水位变动是膨胀土边坡失稳的主要原因;且大多数的滑坡都是在降雨期间或降雨后的短时间内发生的[1-2]。研究发现，季节性的干湿交替变化，导致边坡内膨胀土发生反复胀缩，浅表层土体裂隙发育，这将给雨水入渗提供良好通道[1-3]。降雨后雨水入渗过程中，局部土体含水量显著增加，同时边坡土体出现显著的膨胀隆起变形。而边坡内部土体由于吸水软化，强度可能大幅地降低，并将可能最终导致边坡发生大变形和失稳破坏[4-6]。现有的观测技术可以方便、可靠地记录边坡不同区域的变形数据，可为判断膨胀土边坡发生失稳的可能性提供参考依据 [7-9]。

鉴于问题的复杂性，深入分析雨水入渗过程中边坡含水量及变形的发展规律对于揭示膨胀土边坡的失稳机理十分有必要。本文给出了一种简化的裂隙模拟方法，结合非饱和渗流理论和所发展的工程实用的膨胀变形计算模型开发了可用于工程边值问题的有限元数值程序。基于工程实例模拟了裂隙膨脹土边坡的降雨入渗过程和变形演化过程，初步验证了所提方法和编制的数值程序合理性和可靠性，并进一步深入分析了裂隙膨胀土边坡入渗过程的孔压、含水量和变形规律，探讨了膨胀土变形破坏的特点和机理。

1 裂隙膨胀土边坡的非饱和渗流

1.1 裂隙的模拟

膨胀土在季节性的干湿变化过程中会产生干缩湿胀变形，土体内部形成延展长度大、深度大的裂隙。不少学者对膨胀土裂隙的演化特性开展了室内试验[10-11]和现场调研[12-14]。现场调研的统计资料显示膨胀土风化作用的影响深度大致在2～4 m之间，大多数裂隙发育深度在2 m以内，极端情况下裂隙发育可达7 m[12]。裂隙的发育程度还与深度有关，浅层土体受降雨和蒸发作用的影响较大，形成时间早，裂隙发育程度高，深层土体由于受外部环境的影响比较小，裂隙发育程度较低。

膨胀土在干湿循环作用和加载作用下产生裂隙，对膨胀土的渗透性产生极大的影响。裂隙的开裂与闭合，不仅与水的作用相关，且与应力状态相关[15]。本文假设存在一个临界地表基质吸力sc，当表层土的吸力s大于sc时，土体才会开裂[16]，当吸力s小于sc时，裂隙完全闭合，裂隙及风化土体的渗透系数与原状土相同。且假设s大于sc时，裂隙及裂隙土渗透系数随基质吸力的增大而线性增大，土层的渗透系数采用式（1）计算。

式中：sm为参考基质吸力值;km为s=sm时裂隙或裂隙土层的渗透系数;kc为s=sc时的渗透系数。当s≤sc时，土层中的裂隙假定为完全闭合，假定渗透系数与无裂隙土层相同。无裂隙土层的渗透系数采用Van Genuchten（1980）提出的方程计算见式（2）。

式中：k（s）为吸力s下的渗透系数;ksat为饱和状态的渗透系数;a为与进气值相关的材料参数（kPa-1）;n、m为材料参数，且有m=1-1/n。

1.2 裂隙膨胀土边坡的非饱和渗流过程模拟

二维非饱和非稳态渗流分析的控制微分方程见式（3）。

式中：k为土体的渗透系数;H为总水头;θ为体积含水量;Q为施加的边界流量;t为时间。总水头H可由孔压uw和位置水头H0定义见式（4）。

式中：gw为水的容重。同时，体积含水量θ和渗透系数k均可表达为孔压uw的函数。

土水特征曲线（SWCC）定义了体积含水量和吸力的关系，基于VG模型SWCC曲线可表达为式（5）。

式中：θr为残余体积含水量;θsat为饱和体积含水量;s为基质吸力，且s=ua-uw，ua为孔隙气压，可假定其等于大气压力;参数a，n，m的含义与式（2）相同。

2 工程实用的胀缩变形计算模型

Tripathy等（2002）[17]和Basma等（1994）[18]的试验表明，膨胀土在经历多次干湿循环后将达到一个干湿胀缩变形可逆的稳定状态。自然环境中的膨胀土大都经历过多次干湿循环，可认为达到了稳定状态。Tripathy等（2002）[17]和唐朝生和施斌（2011）[19]开展了重量含水量控制的膨胀土干湿循环试验。唐朝生和施斌（2011）[19]试验结果表明脱湿过程中，在重量含水量大于缩限含水量时，孔隙比与重力含水量间的变化关系呈线性关系;Tripathy等（2002）[17]的试验发现在稳定状态下，吸湿和脱湿过程中，重量含水量和孔隙比关系曲线重合，且当重量含水量大于缩限到饱和度小于80 %左右之间时，孔隙比与重量含水量间变化关系呈线性关系。基于上述试验结果，对处于稳定状态下的膨胀土，建议采用如下简化公式计算干湿胀缩变形见式（6）。

式中：ws为缩限对应的重量含水量，Gs为土粒比重，e0为初始孔隙比。

由于渗流计算过程采用了体积含水量为基本变量，为了方便实现数值编程，需要确定体积含水量与体变间的关系。重量含水量与体积含水量间的关系为式（7）。

由此可得干湿胀缩体变与体积含水量变化间的关系见式（8）。

式中：qs为缩限对应的体积含水量;evp为荷载变化引起的体变，本文采用BBM模型（Aloson等，1990）[20]进行计算，在此不再赘述;evs为含水量变化引起的体变。

3 现场试验结果的模拟

基于所提出的工程实用的膨胀土胀缩变形计算模型，结合非饱和渗流理论和裂隙的模拟方法，自主开发了可用于雨水入渗条件下边坡工程边值问题计算的二维有限元数值程序。结合工程实例开展降雨入渗条件下，考虑裂隙存在时膨胀土边坡的含水量、孔压和变形演化过程的模拟。

3.1 现场原位试验概况

詹良通等（2003）对湖北枣阳某边坡开展了现场原位试验[6]。该试边坡地开挖于1970年，几何尺寸及地层情况见图1（a）。试验边坡中的主要土层是棕黄色的硬黏土，具有明显的胀缩特性。边坡表面裂隙，有的张开度达10 mm，延伸深度达1～1.5 m。上坡面裂隙较下坡面裂隙发育。深度1.5 m以下土体密实度较高，裂隙发育不明显。现场通过在坡面布置喷头进行降雨模拟，降雨量如图2所示。边坡上坡面R1处、中间平台处R2、下坡面R3处分别安放了用于测量土体孔压与变形的仪器。降雨停止期间，边坡蒸发量为2～8 mm/d。

3.2 数值模型及材料参数

据现场勘查结果，浅层为含裂隙的棕黄色黏土，数值模拟中将该土层设定为裂隙发育区。将裂隙单独考虑，简化竖向发育延伸的裂隙，沿土层表层间隔排列。假定坡顶、上坡面裂隙间距为0.5 m，下坡面、坡底处裂隙间距取0.8 m。同时考虑浅层土体内裂隙发育严重程度沿深度逐渐降低，将浅层含裂隙的棕黄色黏土划分为两个区域，I区为表层覆盖层，深度范围0～1.0 m，为裂隙强发育土层;II区位于表层覆盖层下，为厚度0.3～0.5 m的裂隙中等发育土层。浅层含裂隙的棕黄色黏土层以下土体不考虑裂隙的影响的III区。简化后的边坡计算模型如图1（b）所示。

数值模拟中采用与原试验一致的降雨范围及降雨量，如图1（a）和图2所示。期间考虑停止降雨时，边坡存在轻微潜在蒸发，试验阶段的8月26日至9月7日期间取蒸发量为2 mm/d。边坡左右两边及底部边界条件取不透水边界。考虑到表层少量覆盖杂草植的影响，在边坡表层增加了厚度0.003 m覆盖薄层，其材料性质同I区土体且不考虑裂隙的影响。同时考虑在试验开始前，土体处于一个相对干燥的条件，但是由于缺乏前期的降雨和蒸发数据，为模拟降雨前边坡初始孔压分布，模拟降雨前的孔压分布，在坡面施加壓力水头为-6 m的初始条件。

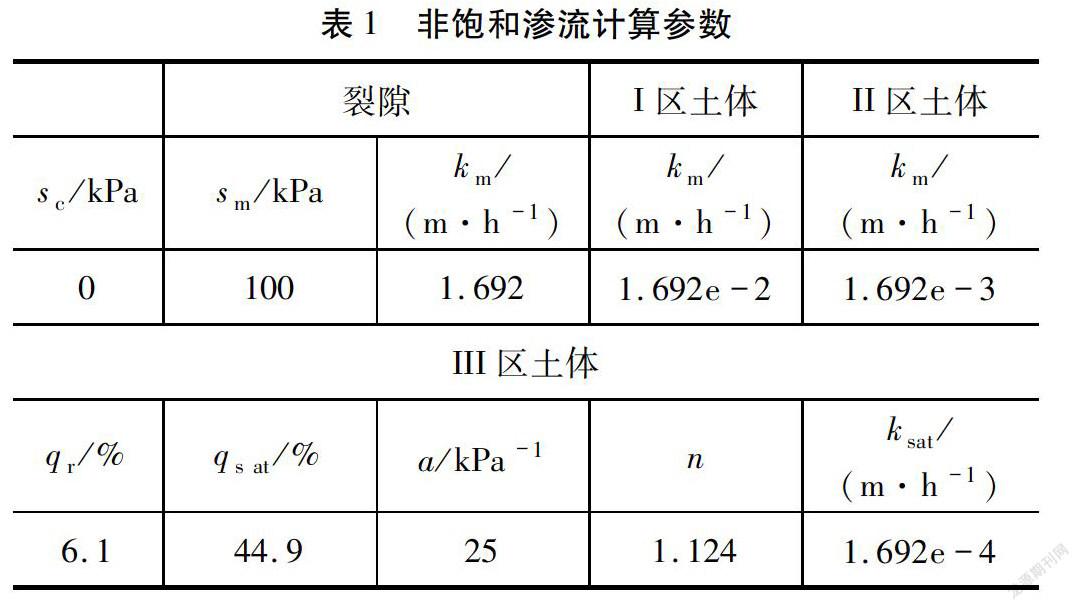
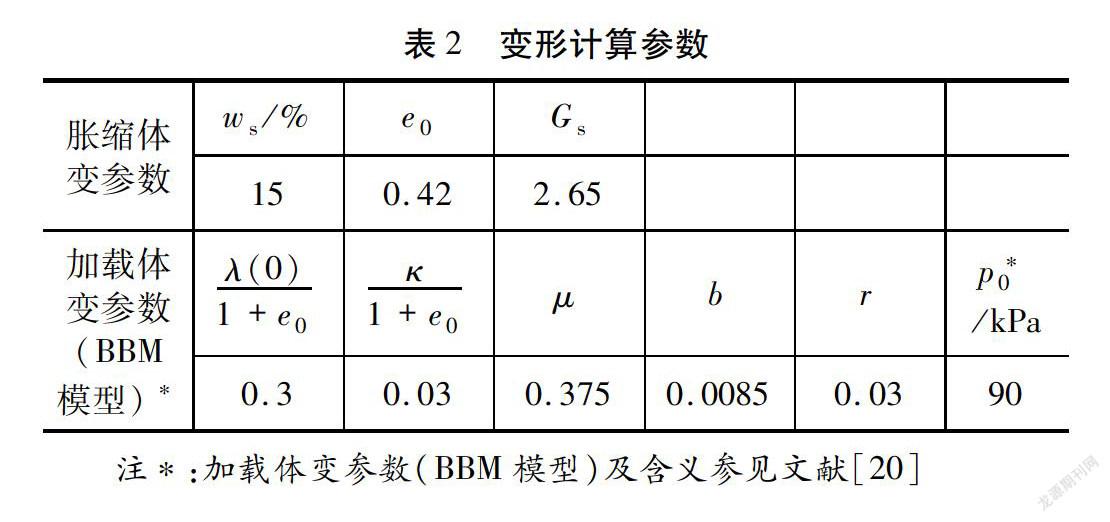
数值计算的参数见表1和表2。III区土体，裂隙不发育，其土水特征曲线及渗透系数参考文献[21]试验结果。I区、II区土体和裂隙的渗透系数在渗透系数的数量级的变化的基础上参考III区土体给出。考虑边坡开挖时间距离试验时间较长，经过长期的干湿反复变化，可认为土体已达到稳定状态，可采用本文给出的工程实用的胀缩变形计算模型。

4 数值模拟结果

4.1 含水量变化过程的模拟结果

图3给出了现场试验降雨过程 R2监测剖面处4个不同深度处含水量探头监测到的含水量变化曲线与相应的数值计算曲线。在第一次降雨过程中，初始3～4 d三个深度处的土体含水量均迅速升高并达到稳定，后续的降雨过程总土层含水变化不大;第二次降雨过程中，土层含水量迅速增大并趋于稳定。对比可见计算结果与实测结果吻合良好。

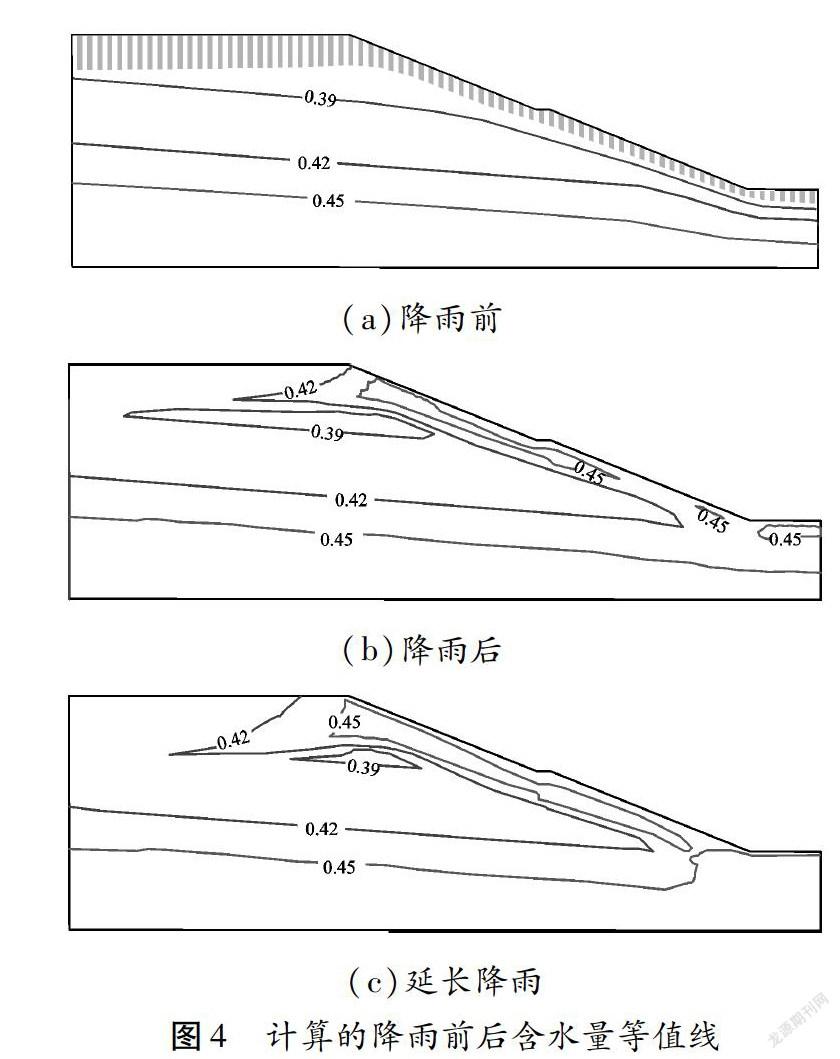
为了进一步整个坡体含水量的变化情况，图4给出了数值模拟中计算的含水量等值线图。图4（a）中给出了在蒸发作用下土层含水量沿深度梯度变化的蒸发剖面的初始状态。图4（b）给出了试验降雨结束后，边坡含水量的变化云图。图4（c）给出了试验结束后，按最后一天降雨量延长降雨10 d，含水量的分布云图。如图4（b）所示，在坡面降雨的情况下（坡顶和坡底处无喷淋系统），由于裂隙发育程度、地形和所处位置不同，土体的饱和区域主要集中在上坡面、中间平台和坡脚处的浅层土体。上坡面R1处，由于裂隙较下坡面发育，因此雨水入渗导致该处含水量在裂隙发育的深度范围（1.5 m深）含水量增加至饱和。中间平台R2处，在雨水通过裂隙入渗和由平台地形带来的内部含水量渗流的共同影响下，含水量变化范围略深于裂隙的发育深度，在约为2.0 m的范围内的土层区域含水量达到饱和。在下坡面R3处，由于裂隙发育程度较弱，且地表径流带走部分雨水，入渗的雨水较少，饱和区域主要集中在裂隙底。同时在坡脚处，在模拟降雨仅发生在坡面的情况下，由于地表径流带来部分雨水，通过裂隙入渗和土层内部渗流，导致坡脚含水量增大，饱和区域略深于裂隙深度。对比图4（b）和（c）可见，降雨延长后，入渗导致的饱和区扩大主要集中在浅层区域和坡脚地带，坡面和坡脚的饱和区即将形成连通的饱和区。

4.2 孔压的模拟结果

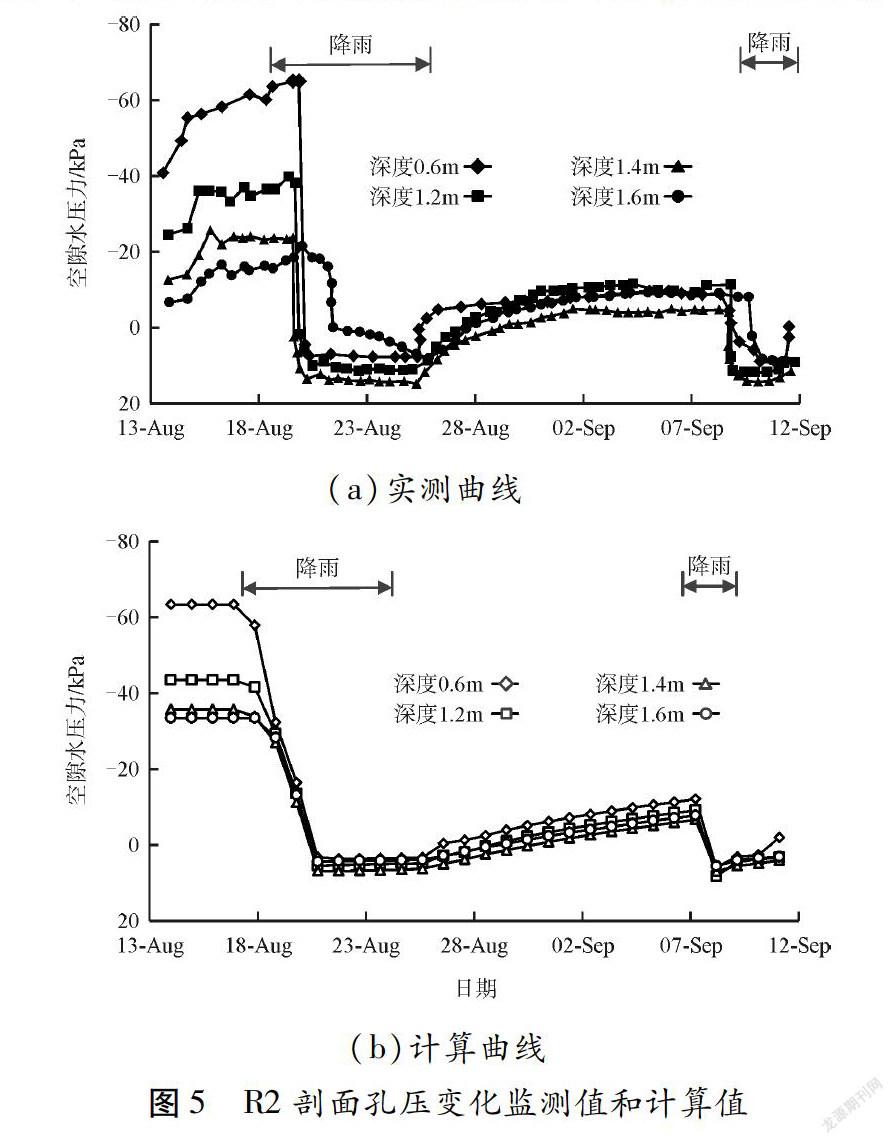
图5给出测断面R2处4个不同深度处张力计测量的孔压的结果和计算结果。对比可见，数值模拟的结果与现场实测结果的含水量和孔压的变化规律具有较好的一致性。降雨后，含水量迅速增加，部分土层区域达到饱和，负孔压（或吸力）短期内降低至零后部分土层出现显著的正的孔压。降雨后的孔压分布规律和含水量变化过程具有较好的一致性。负孔压的降低将导致土层出现软化和强度降低的现象，计算表明这一变化集中在含水量增高的土体的浅层区域和坡脚处（图5）。与此同时，浅层土体含水量增加将增加边坡的下滑力。下滑力增加，土层强度降低，将可能触发浅表型滑坡。

4.3 边坡变形的模拟结果

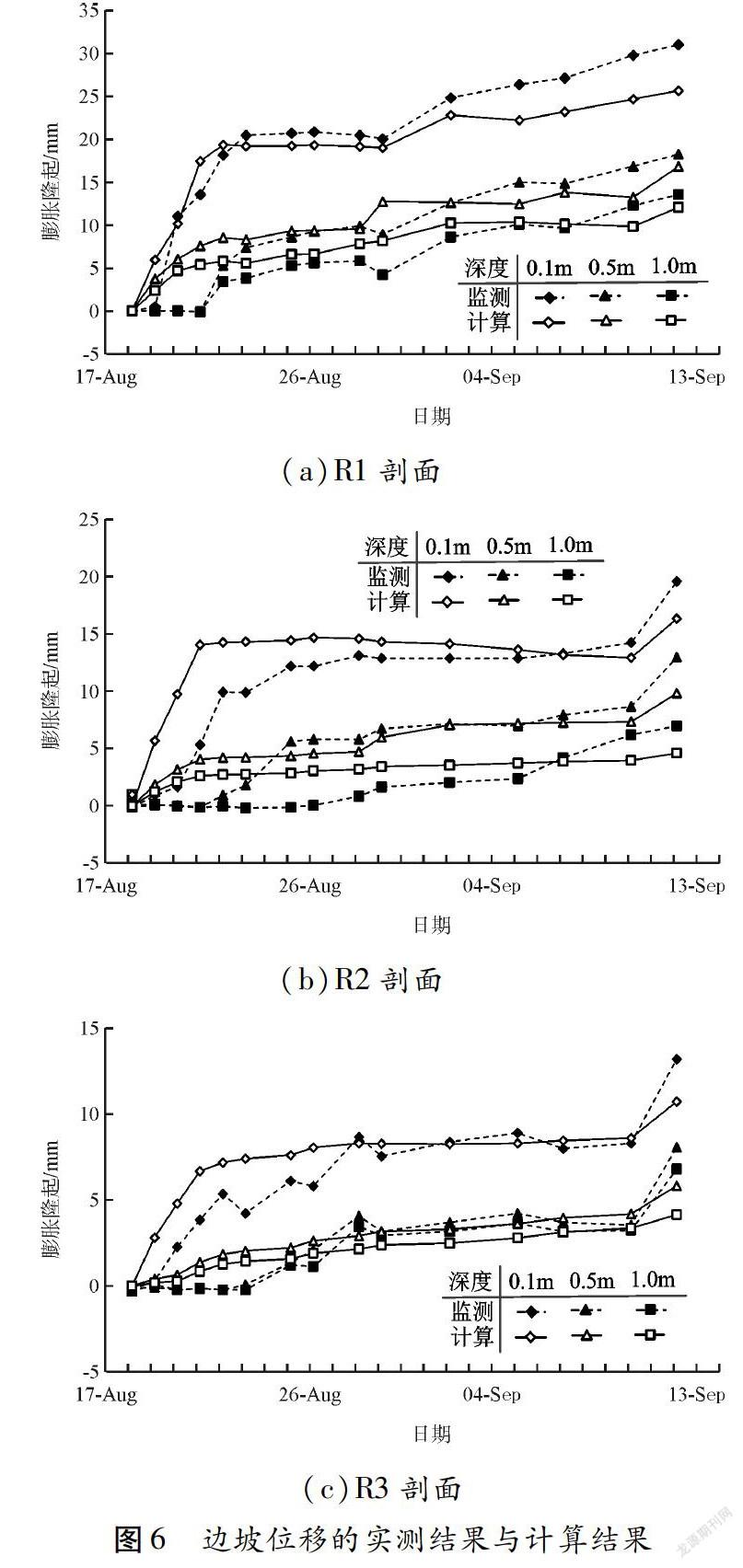
图6给出了3个监测断面处试验监测的不同深度的膨胀量与本文数值方法模拟计算的膨胀量的对比曲线。从膨胀量的大小和发展规律来看，数值模拟较好地再现了膨胀变形的发展过程。对比3个监测断面的膨胀量，可见R1处的膨胀量较其他两个断面要大，R3处的膨胀量最小。由图4计算得到的降雨结束后含水量的分布情况，可以发现，胀缩量与含水量变化具有较好的一致性。由计算结果可见，入渗的雨水主要滞留在裂隙的底部，因此导致局部区域土层内孔隙水压力增大，有效应力降低，土体出现软化和隆起变形。同时，在斜坡表面上出现明显的水平位移，裂隙底部土层发生的水平位移将推动临近土体向临空面发生位移，同时产生水平方向的推力。这也进一步揭示了降雨入渗后裂隙发育的膨胀土边坡容易出现浅层滑坡的内在机理。

5 结论

膨胀土边坡浅表层土体裂隙发育，将给雨水入渗提供良好通道，进而对膨胀土的含水量的变化以及胀缩变形的发展产生显著影响，这决定了膨胀土边坡的变形破坏模式。首先，根据裂隙发育特点，建议了一种简化的裂隙模拟方法和考虑裂隙的非饱和渗流方法;其次，给出了稳定状态下的工程实用的膨胀土变形计算模型;再次，开发了可用于工程边值问题的有限元数值程序，并模拟了降雨条件下裂隙存在时膨胀土边坡的降雨入渗过程和变形演化过程。数值模拟的孔压与含水量的结果与现场试验结果具有较好的一致性，初步说明了所提出数值模拟方法和所编制的程序的正确性和可靠性，为进一步详细分析不同工况下膨胀土边坡的变形破坏过程提供了理论基础和数值手段。

数值模拟结果表明：

（1）降雨初期由于裂隙的存在，浅表层含水量迅速增加。此后，由于裂隙随着含水量的增加而闭合，坡体内雨水入渗速度明显减缓。

（2）降雨入渗在边坡表层和坡脚形成了一个浅层的饱和区，在增加降雨时长后，该饱和区略有增加。饱和区范围略深于裂隙的发育区。由于裂隙的闭合，在增加降雨时长后，该区域以下的区域雨水入渗仍然较少，含水量增加不大。

（3）由于雨水入渗和膨胀变形均发生在浅表层，因此表层土体软化明显，这也解释了膨胀土边坡在降雨—蒸发的反复作用下容易形成浅表型滑坡的原因。

参考文献

[1] 姚海林.考虑裂隙及雨水入渗影响的膨胀土边坡稳定性分析[J].岩土工程学报，2001，23（5）：606-609.

[2] 袁俊平， 殷宗泽. 考虑裂隙非饱和膨胀土边坡入渗模型与数值模拟[J]. 岩土力学， 2004， 25（10）： 1581-1586.

[3] 龚壁卫，程展林，胡波，等.膨胀土裂隙的工程特性研究[J].岩土力学，2014，35（7）：1825-1830+1836

[4] Ng， C. W. W.， Zhan， L. T.， Bao， C. G.， et al. Performance of an unsaturated expansive soil slope subjected to artificial rainfall infiltration. Géotechnique， 2003， 53（2）：143-157.

[5] Zhan， L. T.， Ng， C. W. W.， Fredlund D. G.， Field study of rainfall infiltration into a grassed unsaturated expansive soil slope. Canadian Geotechnical Journal 44（4）：392-408.

[6] 詹良通，吴宏伟，包承纲，等.降雨入渗条件下非饱和膨胀土边坡原位监测[J].岩土力学，2003， 24（2）：151-158.

[7] 姚海林，郑少河，李文斌，等.降雨入渗对非饱和膨胀土边坡稳定性影响的参数研究[J].岩石力学与工程学报，2002， 21（7）：1034-1039.

[8] 卢再华，陈正汉，方祥位，等.非饱和膨胀土的结构损伤模型及其在土坡多场耦合分析中的应用[J].应用数学和力学，2006， 27（7）：781-788.

[9] 张良以，陈铁林，张顶立.降雨诱发膨胀土边坡渐进破坏研究[J].岩土工程学报，2019，41（1）：70-77.

[10] 卢再华，陈正汉，蒲毅彬.膨胀土干湿循环胀缩裂隙演化的CT试验研究[J].岩土力学，2002（4）：417-422.

[11] 张家俊，龚壁卫，等.干濕循环作用下膨胀土裂隙演化规律试验研究[J].岩土力学，2011，32（9）：2729-2734.

[12] 殷宗泽，徐彬.反映裂隙影响的膨胀土边坡稳定性分析[J].岩土工程学报，2011，33（3）：454-459.

[13] 廖世文.膨胀土与铁路工程[M].北京：中国铁道出版社，1984.

[14] 包承纲.岩土工程研究文集[M].武汉：长江出版社，2007.

[15] 王晓燕，姚志华，党发宁，等.裂隙膨胀土细观结构演化试验[J].农业工程学报，2016，32（3）：92-100.

[16] 郑少河，金剑亮，姚海林，等.地表蒸发条件下的膨胀土初始开裂分析[J].岩土力学，2006（12）：2229-2233.

[17] Tripathy S.， Subba Rao K. S.， Fredlund. D. G.，  Water content-void ratio swell-shrink paths of compacted expansive soils， Can. Geotech. J. 39： 938-959 （2002）.

[18] Basma， A. A.， Al-Homoud， A. S.， Husein Malkawi， A. I.， et al.1996. Swelling-shrinkage behavior of natural expansive clays. Applied Clay Science， 11（2-4）： 211-227.

[19] 唐朝生，施斌.干湿循环过程中膨胀土的胀缩变形特征[J].岩土工程学报，2011，33（9）：1376-1384.

[20] Alonso， E.E.， Gens， A.， Josa， A. 1990. A constitutive model for partially saturated soils. Géotechnique， 40（3）： 405-430.

[21] 平扬，刘明智，郑少河.降雨入渗条件下的膨胀土边坡稳定性分析[J].岩石力学与工程学报，2004（S1）：4478-4484.