探寻数学之美 体验数学魅力

张屹

[摘  要] 结合理论研究与教学实践，提出探寻数学之美、领悟数学魅力的基本路径，即生活情境中，体验数学的对称美;方法过程中，体验数学的简洁美;思维培养中，体验数学的奇异美;结论背景中，体验数学的人文美.

[关键词] 数学;魅力;思维;方法;情境

数学是美的，其被称为科学的皇后. 在数学的世界里，有许多丰富多彩、让人爱不释手的美. 作为传道授业解惑的教师，如何发掘数学之美？如何让学生感受数学之美？进而提升学生的思维品质呢？这是作为数学教师需要研究的重要课题. 基于此，笔者结合理论研究与教学实践，提出探寻数学之美、领悟数学魅力的基本路径，即生活情境中，体验数学的对称美;方法过程中，体验数学的简洁美;思维培养中，体验数学的奇异美;结论背景中，体验数学的人文美.

生活情境中，体验数学的对称美

七年级学生初次学习几何时，往往难以入门，感到几何知识枯燥乏味，感到有的几何知识似曾相识，但又不知所以然;有的几何知识感到很难，仿佛几何离我们很遥远. 实际上，在生活生产中就存在几何，几何就在我们身边，教学中，教师可创设生活情境，让学生体验几何图形里的美.

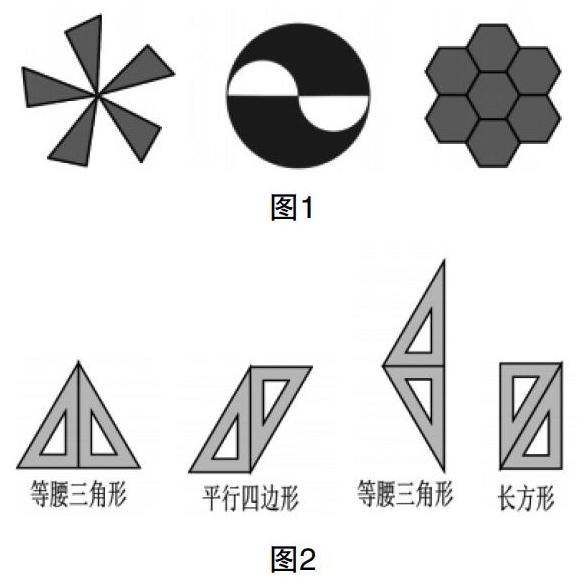
例如，最朴素、最简单的美就是对称美. 在学习对称时，笔者给出了如图1所示的三个图形，前两个图形体现了中心对称之美，第三个图形既有中心对称之美，也有轴对称之美. 学生被这种自然天成的对称美所吸引，列举出了许多生活中的对称图形. 然后，笔者顺势利用两个全等的直角三角形，让学生拼出一个对称图形，如图2所示就是学生拼出的对称图形，通过欣赏对称图形美与拼接对称图形，提升了学生的思维水平.

正方形是最完美的图形，它既是轴对称图形又是中心对称图形，为了提高学生的学习兴趣，笔者提出了“完美正方形”的概念，其是指用一定数量的小正方形拼成一个大正方形，它的神奇之处在于这些小正方形的边长并不相等.学生认为很容易拼出这样一个正方形，而实际上很长时间以来，世界上没有人能够拼出這样完美的正方形，甚至一度有人认为，这是一个不可能存在的事件，到底这样完美的正方形存不存在呢？学生感到很新奇. 此时，笔者告诉学生，一位荷兰的数学家多杰维斯廷于1978年找到了由最少正方形个数拼成的完美正方形，他是用一个巧妙的程序设计出来的. 这些边长彼此不等的正方形，边长分别是2，4，6，7，8，9，11，15， 16，17，18，19，24，25，27，29，33，35，37，42，50，由此形成的完美正方形的边长为112，数学难题终于被破解，学生学习数学的情绪被彻底调动了起来.

其实，让数学知识自然回归，会让学生更加亲近数学，体会到数学的自然之美. 在探寻数学美的过程中，学生会得到解决数学问题的通性通法，当然，这也需要教师在众多的数学之美中进行取舍，回归对自然、生活的感悟与联想.

方法过程中，体验数学的简洁美

在大千世界中，看似杂乱无章，但却蕴含着数学的基本概念、理论与公式. 数学语言就是以一种简洁的形式将其表达出来，呈现给学生以简洁美. 在数学的众多概念、公式、定理中，它们既相互独立，又存在必然的联系，因此教师应把教学过程作为一个动态发展的过程，把数学知识的发生、发展过程进行展现，进而凸显数学教学过程中发现、鉴赏与创造.

通过这一道数学题，再一次展现了数学的简洁美. 本节课由一个分式方程到一个无理式，都采用了相同的方法，即换元法，巧妙地解决了问题，这种变换具有美学意义上的联想. 对称是一种和谐，但是缺乏简洁的对称，会给人以烦琐之感，所以既简洁又对称才是真正意义上的和谐. 教师在教学中要以简洁之美启发学生的智慧，让学生真切感受到数学的魅力所在.

数学探究中，体验数学的奇异美

认识数学的奇异之美，需要打破数学的统一性，实现认识上的飞跃，虽然它是超乎常规的，但也有一定的规律性质. 作为初中生，不可能提出现有数学结论的悖论，一些数学猜想也无法推翻，但初中可以做到的是得到数学中的一些新颖结论，举出一些出人意料的反例或创新解题方法总是可以实现的，它们都表现出了数学的奇异美，往往是新思想、新理论的发源地. 当规律化、程式化的结论出现独创性的成果时，学生的情绪是兴奋的、激动的，其中数学中的一题多解、多题一解都是数学奇异美的表现.

例如，探究n边形内角和公式时，笔者引导学生使用了三种方法，提升了学生的数学探究能力，领略了数学的奇异美.

方法3：在多边形的内部取一点P，如图6所示，将点P与多边形的各个顶点连接，可得n条分割线，把多边形分割分成了n个三角形. 这n个三角形除了组成多边形的内角和之外，还多了一个周角，所以n边形的内角和等于n·180°-360°=（n-2）·180°.

基于以上探究，不难发现，另辟蹊径的方法带来了意想不到的效果，培养了学生的发散性思维与数学的创新能力.

结论背景中，体验数学的人文美

数学规律是人们求真的结果，但把它放在人文背景里，却是求真、求善、求美的高度统一. 博伊指出，教学内容不能受学科范围本身的限制，还要体现人文主义精神. 即要把数学当作一种文化，在课堂教学中把人文精神贯彻下去，如司马光砸缸就与数学知识有关;“孤帆远影碧空尽”就与极限概念有关;王戎推理出路边的李子是苦的是逻辑推理的结果. “万无一失”，是指“有绝对把握”，但这个成语可以联系概率进行思考，有效利用历史事件、成语、诗句，能使数学课堂充满人文美.

总之，孕育数学知识的生活背景是有机联系的，涵盖对称美、简洁美、奇异美、人文美. 教学中，教师应进行充分挖掘，让数学充满美.