强化概念本质凸显转化思想
席莉

基于大单元整合的思想,笔者设计了《多边形的面积》单元开启课——《数面积》。本课从长方形的面积推导过程引入,将平行四边形、三角形、梯形、组合图形等面积计算整体呈现给学生,启发学生以方格纸为支架,自主进行类比、迁移,实现计算方法的转化,使学生形成整体化、结构化、系统化的研究平面图形面积的方法。
一、紧扣已有经验,凸显概念本质
借助方格纸“数”图形面积,可以加深学生对面积及面积单位的理解。学生在学习长方形的面积时,利用“数方格”的方法推导出计算公式。这种活动经验可以运用到其他平面图形面积的研究过程中,让面积单位的度量统一。
课始,笔者用课件依次呈现三幅图(如图1),帮助学生回忆长方形面积的推导过程,引导学生经历“铺满面积单位—只铺关键格数—提取关键要素”三个环节,唤醒学生对面积和面积单位含义的认知:长方形面积=长×宽,实际上是求这个长方形所包含的面积单位的个数。
这样的设计强化了学生对图形面积的本质理解,即选取一个合适的单位进行密铺,再计算出图形所含面积单位的个数。本环节突出“数方格”的作用,为后续的自主探究做铺垫。
二、探究开放问题,感悟转化方法
感知是思维的源泉,为学生提供丰富、典型的直观材料可以促进学生对知识的深度探究。以方格纸作为支架,能帮助学生体会转化策略、感悟数学思想、积累活动经验。
课上,笔者出示学习单和活动要求(如图2),请学生经历独立思考、小组交流、展示汇报的环节,借助方格纸研究下面多种平面图形的面积。
在汇报环节,一名学生选择数平行四边形的面积,他发现沿着高把右边的“三角形”切下来,平移到图形左边,可以把它变成一个长方形,算出它的面积是6×3=18(cm2)。笔者追问:为什么想到要把这一块切下来,补到哪里去呢?学生解释:通过观察发现切割和移补“三角形”可以将不完整的格数变成完整的格数,以便于数出面积,这样做只改变了图形的形状,而没有改变图形的大小。笔者小结:这个“变”的过程就是在“转化”,将平行四边形的面积转化为我们熟悉的长方形的面积。
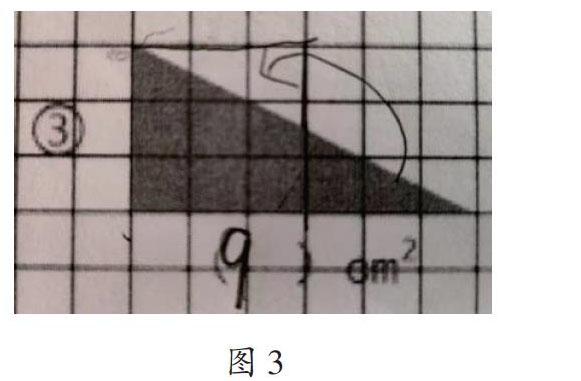
学生对学习单中直角三角形的面积很有兴趣,主要采用了两种研究方法:一是通過割补(如图3)将直角三角形变成正方形,数出面积是9cm2;二是“复制”一个完全相同的直角三角形,将两个直角三角形拼成一个长方形,长方形面积是18cm2,直角三角形的面积是它的一半,也就得到面积是9cm2。
笔者充分肯定了学生的空间想象力,并引导学生思考两种方法的差异。学生发现第一种方法是将直角三角形的一部分切下来,拼补到空白处,将原图形转化成正方形;第二种方法是通过想象两个完全一样的直角三角形拼合成一个长方形,面积比原来翻了一倍,求原直角三角形面积要除以2。笔者乘机总结:根据两种面积转化方法的特点,第一种叫“割补法”,第二种叫“倍拼法”。
在这个环节,笔者提供了一个开放性的大问题,给予学生充分的时间独立思考,让学生主动关联旧知,自主探究新问题。小组内不同转化方法的碰撞,启发了学生的思考,使他们感悟到图形面积转化方法的多样性以及转化思想的一致性。
三、灵活变换图形,形成转化思想
学生之间的交流碰撞、互相启发使解决问题的方法呈现出多样性和个性化。在此基础上,教师帮助学生提炼方法,不断地促进学生内化转化思想,可以让学生对图形转化方法融会贯通,促进学生对转化思想的深度理解。
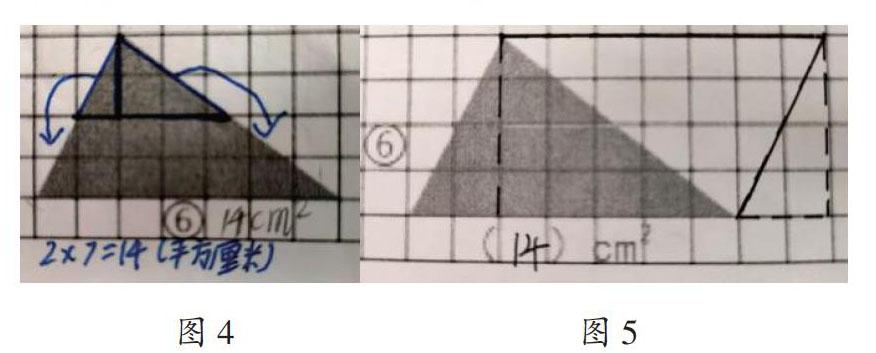
学生在数⑥号三角形的面积时,出现了多种转化方法。有的学生用割补法把三角形的上半部分进行分割(如图4),分别移补到下面,把原三角形转化为长方形,数出其面积为14cm2。有的学生把两种方法结合使用:先沿着高把三角形分成两个直角三角形,再把两个直角三角形分别“倍拼”,变成一个面积是28cm2的长方形,最后用28除以2,求出原三角形的面积是14cm2。还有的学生先用倍拼法把两个完全一样的三角形拼成一个平行四边形,再用割补法沿平行四边形的高把左边的“三角形”切下来平移到右边的空白处,拼成一个长方形(如图5),这个长方形的面积是28cm2,则原三角形的面积是14cm2。
对大问题的自主探究促使学生灵活运用“割补法”和“倍拼法”,将未知的平面图形的面积转化为已知的长方形的面积,并很好地掌握了变化前后图形面积的关系。课的结尾,笔者引导学生猜想圆的面积是如何转化和推导的,让学生的思维持续延伸。
学生通过开启课的学习,加深了对面积的理解,打开了“转化思想”的大门,积累了基本数学活动经验。这节课承上启下,为学生的后续学习做好了理解概念本质、开启转化思维、培植研究方法的准备。
(作者单位:黄石市白马山小学)

