配电系统网络性能及电能质量评估方法

何 涛，李肇卿，刘一涵，杨坤柔，董逸俊

(国网上海市电力公司，上海 200120)

随着网络技术[1]和电力系统[2]的不断普及与发展，电能质量已成为业界和消费者关注的重点。传统的电能质量检测方法主要应用检测技术衡量配电网络性能，目前的主流方法是通过电子测量活动[3]来测量电能质量。

电能质量[4-5]是电压质量和电流质量的结合。电能出现质量问题主要是由于配电网中不断增加的干扰源造成的，这些干扰源就是电网中包含的大量电源、输电线路、变压器和负载。如果电网中没有电压正弦信号，则意味着电网中可能出现中断(连续性问题)、电压平均凹陷、膨胀、谐波、噪声等失真。

为了解决这一问题，国内外学者对配电网中的电能质量进行了大量研究，并取得了丰硕成果。廖建权等[6]对谐波与波动、偏差与稳态不平衡、暂降与暂态不平衡间的关联性进行了分析，并对其在直流电能质量评估、指标限值制定等方面的重要作用进行了研究。冷华等[7]基于层次分析法建立了一套实用型配电网运行状态评估指标体系，并利用模糊隶属度函数确定了单项指标评分公式。姚强等[8]提出的一种适用于电能质量监测的智能检索系统，为电网运行提供了助力。王建波等[9]设计了一种基于电能质量监测平台的次同步振荡在线监测终端系统，提出了一种基于谐波分析、间谐波分析和振荡功率的快速算法，实现了同步振荡在线监测。然而，这些方法大多基于电能质量监测活动后产生的电压测量或电子记录，很少有学者提出在规划或运行阶段评估配电系统电能质量的方法。为了提高规划阶段配电系统的评估水平，有必要对规划阶段的元件可用性进行评估。因此，本文提出了一种混合式电路分析算法。

1 模型介绍

本文所提方法以传统电路分析为基础，结合短路模型、潮流模型及序贯蒙特卡罗算法，不仅能通过持续中断模型评估元件可用性，而且能在配电系统规划阶段结合瞬时中断来感知电能质量的影响。各算法具体实现如下。

1.1 短路模型

本文所提方法以三相线路总线导纳Ybus为基础，充分考虑了各相之间的相互关系。通过应用诺顿定理，短路阻抗矩阵可通过向每个节点注入1 A的电流确定，一次一相，得到的电压将代表短路阻抗ZSC的一列。在节点的每个阶段重复此过程，直到ZSC完全确定为止。此后，每个节点将有自己的ZSC和导纳YSC矩阵，具体定义为:

(1)

进一步，利用ZSC和戴维南-诺顿等效系统，可以得到各种类型的短路电路。对于三相短路，故障电流ISC通过故障前电压VP和节点的YSC获得，如式(2)所示：

ISC=YSC·VP

(2)

由于配电系统通常是不对称和不平衡的(每相的自阻抗是不同的)，因此在三相故障(对称故障)中，各相的短路电流大小也会不同。

同理，对于单相接地短路，故障电流If可由故障前电压与故障相自阻抗的关系求得，如式(3)所示：

(3)

式中：Rf为故障电阻。

在计算出故障电流后，短路电流引起的偏差电压ΔV如式(4)所示。可以应用叠加定理计算出发生故障后的电压VPo,由式(5)求出：

(4)

VPo=VP+ΔV

(5)

1.2 潮流模型

馈线上的三相潮流计算执行步骤如图1所示，图中V为瞬时电压，VC为阈值电压，具体计算步骤如下。

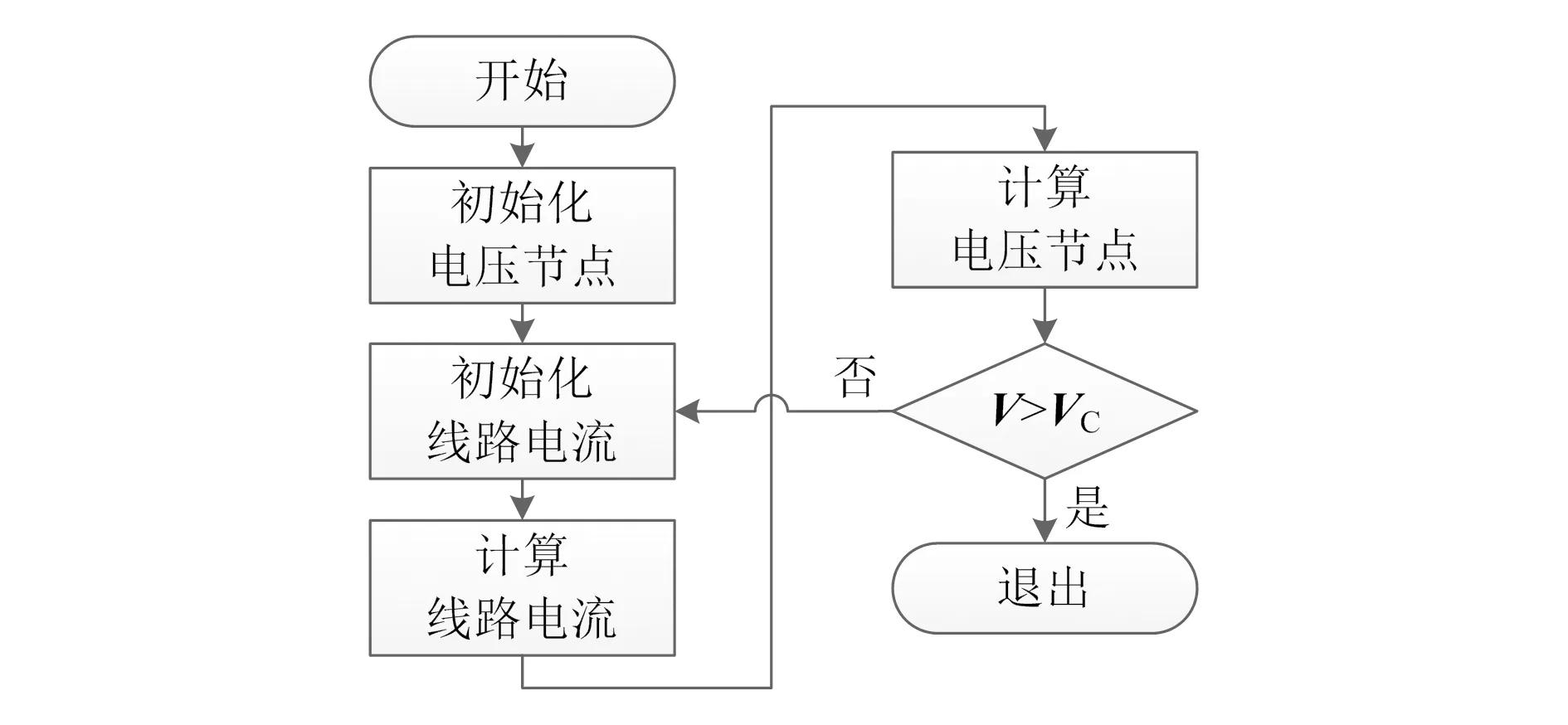
图1 基于电流总和法执行步骤

步骤1，用近似解初始化电压节点，并启动迭代计数器。

步骤2，连接设备用与负载类型相关的负载电流初始化线路电流。

步骤3，根据式(6)计算从终端节点到变电站节点的线路电流。

(6)

步骤4，根据式(7)和(8)计算从变电站节点到终端节点的电压。

(7)

(8)

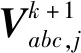
步骤5，更新迭代计数器并验证收敛性。如果剩余电压大于规定阈值，则返回步骤2；否则，停止仿真。

1.3 序贯蒙特卡罗算法

序贯蒙特卡罗算法[10]可以准确再现中断周期，从而模拟每个组件可能发生的故障。利用马尔可夫模型表示故障，可以估计出系统中每种保护方案的负荷损失指标以及与电能质量相关的指标。此外，规划者可以选择系统可靠性的最佳替代方案，并为用户确定敏感负载的安装位置。本文提出的序贯蒙特卡罗算法按照以下步骤执行。

步骤1，基于蒙特卡罗算法的潮流计算方法得到稳态电压。

步骤2，定义相对误差β和仿真的最大迭代次数，并对每个组件的初始运行状态进行取样。

步骤3，对组件可用或不可用期间进行采样。

步骤4，确定下一个状态，明确各部件的最短状态持续时间。

步骤5，评估所选状态，如果是成功状态，则转到步骤4；否则，执行步骤6。

步骤6，确定采样短路类型，计算受影响相位和故障电阻，同时计算各节点的故障电流和故障时电压。

步骤7，基于马尔可夫模型，对失效状态进行抽样。

步骤8，更新测试结果及相应指标。

步骤9，如果时间达到规定阈值，则存储索引，更新其相对误差并转至步骤7；否则，返回步骤3。

步骤10，如果达到最大迭代次数或可靠性指标的相对不确定度小于规定阈值，则仿真停止；否则，开始新的迭代并返回步骤3。

2 仿真分析

为了评估不同保护方案和网络几何模型对可靠性指标的影响，本文设计了图2所示的具有16个节点的配电系统。该配电系统从单相分支到三相分支，其几何结构类似于IEEE 13和34节点试验馈线中使用的架空线路。假定系统由一台115/24.9 kV变电站变压器供电，该变压器连接在电源总线和第一个节点之间。系统存在不平衡现象，且所有类型的负载(P(有功功率)、Q(无功功率)、Z(阻抗)、I(电流))以Y形或三角形连接。系统中主要有2个高负荷中心，其中一个为节点6(500个用户，其中C表示用户)；另一个为节点10(拥有1 500个用户)。本文假定系统中各支路永久性和暂时性故障率分别为0.5次故障/(km·a)和4.0次故障/(km·a)，且系统不考虑干线或横向故障。

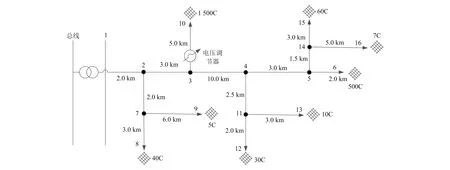
图2 系统设计方案

为了验证电网几何模型对电能质量指标影响的结果，本文给出了一个典型案例：图2所示的系统中变电站输出包括1个断路器(带重合闸继电器)、7个分支熔断器、1个重合器(线路3-6断路器)和1条附加线路(带NO(常开)开关，当线路3-10停机时，该开关闭合)。

表1所示为规则几何和垂直平行几何两种几何结构下的电能质量性能指标系统平均停电频率(system average interruption frequency index，SAIFI)、系统瞬时平均均方根变化频率指数(system instantaneous average RMS variation frequency index，SIARFI)、系统暂时平均均方根变化频率指数(system momentary average RMS variation frequency index，SMARFI)和系统暂时电压变动平均次数指数(system temporary average RMS variation frequency index，STARFI)的对比结果。可以看出，规则几何模型电能质量明显优于垂直几何模型。因此，不同的网格拓扑结构意味着导体之间的不同距离，从而导致互阻抗和互电势系数的改变。

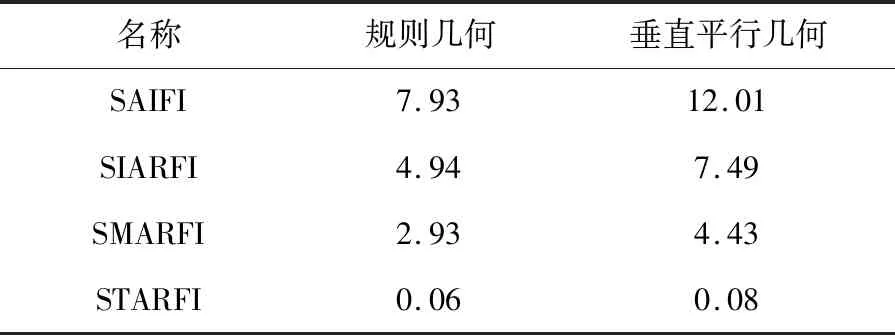
表1 不同模型下电能质量对比结果

图3所示为电网几何模型对所有规划方案电能质量指标的影响结果，可以看出，利用垂直平行几何结构可有效减少电网中电压骤升次数。实验结果进一步验证了本文所提方法的有效性。

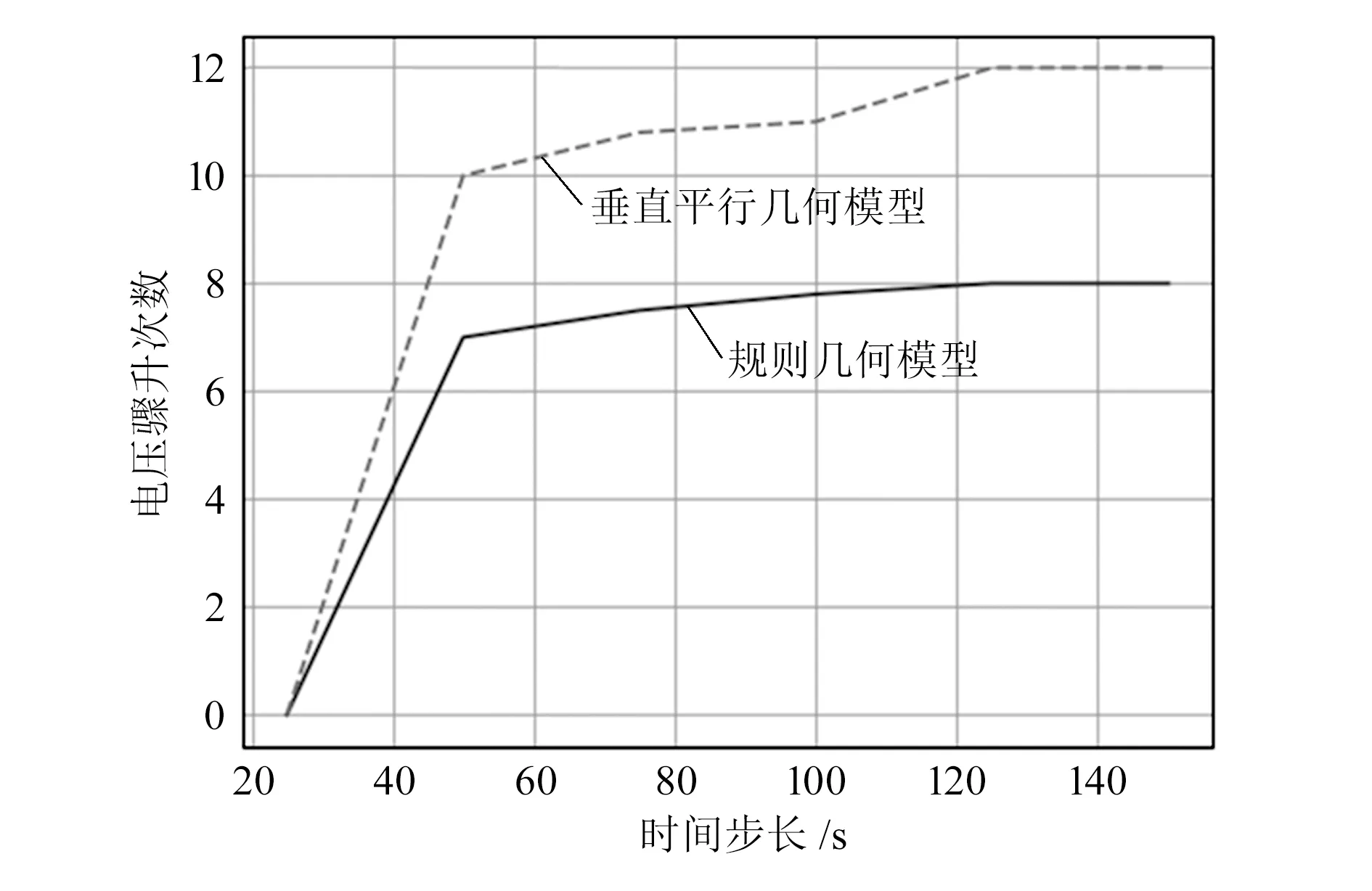
图3 不同模型对电能质量指标的影响

3 结束语

传统的电能质量监控主要是通过电子测量活动来进行的，很少有针对规划阶段配电系统评估水平的研究。针对这种情况，本文以传统电路分析为基础，结合3种经典算法(短路模型、基于电流总和法的潮流计算模型、序列蒙特卡罗算法)，在规划阶段评估配电系统的电能质量。未来可对谐波有功功率和无功功率的电能质量及可靠性进行评估，进一步提高配电网评估质量。此外，对电能质量监测布设位置进行优化，还能进一步节约成本。