烟囱定向爆破拆除前冲及塌落触地振动研究
费鸿禄,王 帅,钱起飞
(辽宁工程技术大学 爆破技术研究院,阜新 123000)
近年来,由于城市改建、扩建工程进入大规模的发展阶段,因此拆除建(构)筑物的需求也越来越大[1]。与传统拆除方法相比,拆除爆破是清除废旧建(构)筑物的一种实用、经济、高效、安全的方法。但这项高危作业,尤其是在城市地区,可能会引起邻近居民不必要的恐慌,且若待拆除的建(构)筑物自身结构、周边环境极其复杂,则任何微小的错误都可能导致悲剧的发生[2,3]。因此,在当前情况下对建(构)筑物爆破拆除整个过程及危害效应的研究益加重要。
控制爆破是钢筋混凝土烟囱拆除的主要方式之一,为确保爆破拆除过程更加精细、安全,广大学者对钢筋混凝土烟囱爆破拆除的相关领域进行了大量的研究。由现场观测或数值模拟结果可知[4-7]:钢筋混凝土烟囱定向爆破拆除倒塌过程主要分为爆破切口形成、中性轴形成及后移、定向倾倒和塌落触地4个阶段。在爆破切口形成后,余留支撑部位通常都会经历中性轴未形成期和中性轴稳定期两个阶段,中性轴的后移由烟囱自重和拉区弯矩形成的载荷与压区抗力的纵向平衡决定[7-9]。烟囱在定向倒塌过程中可能会伴随有前冲、下坐、后坐或空中折断的发生。爆破切口形成瞬间由上部筒体产生的突加荷载[7]、中性轴的后移[8,9]、烟囱自身结构特征及爆破切口参数是造成烟囱下坐的主要原因;烟囱的后坐、前冲、空中折断则与烟囱的爆破切口形状、倾向倒塌运动状态及筒体材料的力学性能密切相关[10-12]。大量工程实测数据表明,在塌落触地阶段建(构)筑物连续塌落诱发的塌落振动对周围建(构)筑物的危害最严重[13],因此周家汉、Lin F等分别建立筒形类高大建(构)筑物爆破拆除塌落振动速度计算模型[14,15],对建(构)筑物爆破拆除塌落诱发的振动进行预报。
工程实践表明:烟囱定向爆破拆除过程中的前冲决定着烟囱倒塌范围和塌落振动的大小,且与烟囱的触地姿态密切相关。烟囱爆破拆除尽管已经达到了可控性,但烟囱爆破拆除过程中前冲仍是一个威胁着拆除安全、成功的问题。本文基于烟囱定向爆破倾倒过程力学分析,结合实际爆破拆除工程,对烟囱的前冲机理进行深入探究;然后从烟囱的触地姿态入手,对前冲过程进行深入分析;最后在此研究的基础上对烟囱的塌落触地振动进行研究。
1 烟囱定向倾倒过程力学分析
钢筋混凝土烟囱从爆破切口形成瞬间到切口上部筒体触地解体之前,烟囱在自身倾覆力矩作用下定向倒塌。通过观测以往烟囱爆破拆除效果[4],可以发现从爆破切口形成后至切口闭合前,烟囱绕余留支撑部中性轴发生缓慢定轴转动;切口闭合之后,烟囱以切口下沿对应的预留体为转轴定轴转动。为简化分析,假设在定向倾倒过程中烟囱完好未发生解体破坏,切口截面平整,忽略空气阻力、爆炸荷载对烟囱倾倒过程的影响。
如图1所示,根据达朗贝尔原理列出下列平衡方程

图 1 烟囱定向倾倒受力分析简图Fig. 1 Force analysis diagram of chimney directional dumping
(1)
式中:m为切口部位薄弱截面以上部分烟囱质量;g为重力加速度;N、R分别为支座反力的径向力、切向力;ε为切口闭合之后阶段烟囱定向倾倒的角加速度,设烟囱倾倒方向为正,根据拉格朗日方程可求得
(2)
ω为切口闭合之后阶段烟囱定向倾倒的角速度,根据机械能守恒定律可求得
(3)
式中:l为切口闭合之后阶段切口部位薄弱截面以上部分烟囱质心到转轴的距离;Jb为切口闭合之后阶段烟囱的转动惯量;θ0为切口闭合之后阶段烟囱的初始倾角,θ0=α0-θ1;α0为切口闭合角;θ1为切口闭合之后阶段烟囱质心与转轴连线与烟囱中线的夹角;θ为切口闭合之后阶段烟囱的瞬时倾角;εb为切口闭合瞬间烟囱定向倾倒的角加速度
ωb为切口闭合瞬间烟囱定向倾倒的角速度

式中:lb为切口闭合瞬间切口部位薄弱截面以上部分烟囱质心到中性轴的距离;φ0为切口部位薄弱截面以上部分烟囱质心与中性轴的连线与竖直方向的夹角;JA为切口闭合瞬间烟囱的转动惯量;Mα0为切口闭合瞬间支撑部位的残余塑性铰弯矩;Mφ为转角为φ时对应的塑性铰弯矩,可根据下式进行计算[16]
Mφ=Mbcos(φ/2)
式中:Mb为支撑部位的塑性铰极限抵抗弯矩[17]
式中:fct、fcc分别为混凝土的抗拉和抗压强度;fst、fsc分别为钢筋的抗拉和抗压强度;ρ为烟囱切口部位的纵筋配筋率;Mct、Mcc分别为受拉区、受压区混凝土的极限抵抗弯矩,可由下式进行计算

将上述结果带入(1)式整理可得
(4)
因此,烟囱定向倾倒过程中的水平和竖向支座反力Fx、Fy分别为
(5)
2 烟囱定向倾倒前冲分析
烟囱在定向倾倒过程中,当倾倒至某一角度时往往会伴随着前冲的发生[11]。对该问题的研究,可在烟囱定向倾倒受力分析的基础上对烟囱的前冲机理进行分析,根据分析结果对前冲过程进行研究。为简化分析,假设烟囱在前冲瞬间与支撑部位相连的钢筋已经被拉断。
2.1 前冲机理分析
烟囱在定向倾倒过程中,由于烟囱在自重作用下倾覆造成烟囱发生前冲现象,尤其是在高位切口烟囱爆破拆除过程中。对于前冲问题可从两个角度进行分析:一是烟囱定向倾倒过程中支座反力的径向力(又称前冲力)大于零,即认为当前冲力大于零时,烟囱将脱离支撑部位发生前冲;二是烟囱倾倒过程中的水平支座反力大于该瞬间支撑部位提供的摩擦力,即认为烟囱在定向倾倒过程中,随着倾角的增加,支撑部位提供的摩擦力小于该瞬间烟囱的水平支座反力时,烟囱将发生前冲。本节分别从这两个角度进行分析,并与实际工程进行对比,找出烟囱前冲的原因。
判据一:当N=0时,则
判据二:为方便分析,令F为等效力,则当F=Fx-|μ1Fy|=0时,烟囱即将发生前冲。将该式带入MATLAB软件中进行求解可得[θ]值。
式中:[θ]为烟囱即将发生前冲时的转角(下文简称前冲倾角);μ1为支撑部位的摩擦系数[18],本文在理论计算时取μ1=0.7。
由上述分析可知,当烟囱定向倾倒至转角[θ]时,N、F的方向将发生改变,在不发生较大范围后坐的情况下,烟囱将脱离支撑部位做近似平面运动,即前冲。
2.2 前冲过程分析
爆破切口形成后,烟囱在自身重力作用下定轴转动,当转动至前冲倾角[θ]值时,由于受力状态发生了改变,烟囱原有的动态平衡被打破,烟囱将开始发生前冲。根据文献[19]可知:烟囱的前冲可分为两部分,一是烟囱从开始前冲至触地瞬间的运动,二是烟囱触地后克服摩擦力在地面上的运动。为便于表述,设烟囱从开始前冲至触地瞬间的运动为一次前冲,烟囱触地后克服摩擦力在地面的运动为二次前冲。
由2.1节分析可知:烟囱在发生前冲瞬间,有
(6)
2.2.1 一次前冲
由相关力学分析可知,烟囱的一次前冲可近似分解为绕质心的转动和随质心的平抛运动[]。在烟囱定向倾倒过程中,由于其触地姿态的不同会导致其前冲范围不同,为对前冲范围进行分析,因此需根据烟囱不同的触地姿态分别进行讨论。
(1)烟囱水平触地
设烟囱以水平落地姿态触地时烟囱下坐完成瞬间所在截面(后文简称烟囱下坐完成截面)距地面的高度为H0,该种情况的受力分析见图2,根据烟囱落地过程中的运动规律有
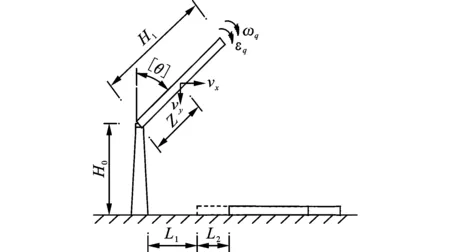
图 2 烟囱水平触地情况Fig. 2 Horizontal grounding of chimney
(7)
式中:t1为烟囱发生一次前冲所经历的时间,由(7)式可得
根据烟囱落地的运动规律及几何关系有
(8)
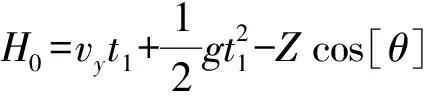
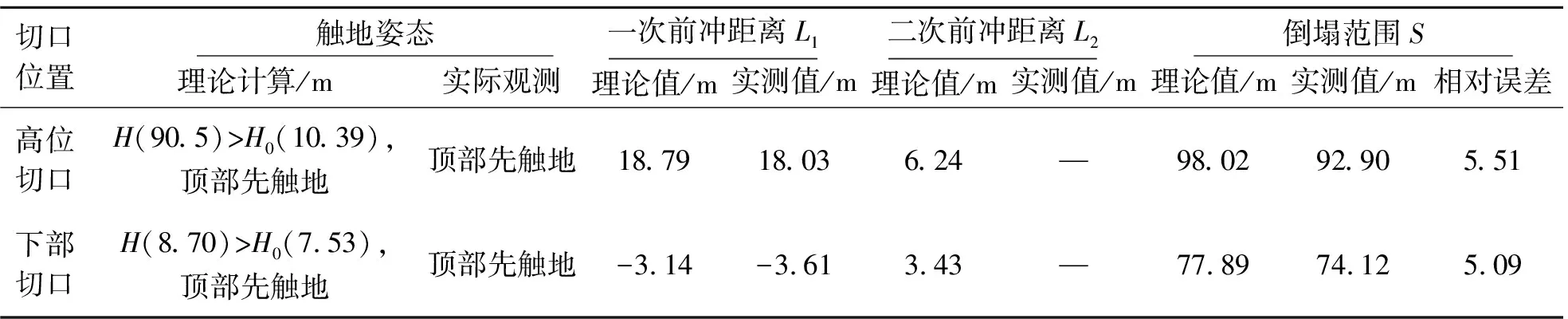
(2)烟囱底部先触地,即H 此时,受力分析见图3,根据烟囱前冲过程的运动规律及几何关系有 图 3 烟囱底部先触地情况Fig. 3 The bottom of the chimney touches the ground first (9) 将式(9)带入MATLAB软件中求解得t1。 (3)烟囱顶部先触地,即H>H0 此时,受力分析见图4,根据烟囱前冲过程的运动规律及几何关系有 图 4 烟囱顶部先触地情况Fig. 4 The top of the chimney touches the ground first H+Zcos[θ]-(H1-Z)cos(π-[θ]-ωqt1)= (10) 式中:H1为切口部位薄弱截面以上部分烟囱的高度。同理将式(10)带入MATLAB软件中求解可得t1。 2.2.2 二次前冲 烟囱触地后,筒体发生破碎或断裂,但由于烟囱在触地瞬间仍存在着水平加速度分量,且钢筋混凝土烟囱的强度较高,因此烟囱在触地后部分筒体会发生二次前冲。为保守分析,设烟囱在触地瞬间未完全发生解体破坏,如图2~图4所示,根据二次前冲的运动规律有 vx=μ2gt2 (11) 烟囱一次前冲的前冲距离理论上为烟囱从开始前冲到触地瞬间的水平位移量减去烟囱倾倒过程中的后坐和下坐量[20],即 L1=l1-l2-l3-R2 (12) 式中:L1为烟囱发生一次前冲的前冲距离;l1为烟囱从开始前冲到触地瞬间的水平位移量,l1=vxt1;l2、l3分别为烟囱倾倒过程中的后坐量、下坐量;R2为烟囱底部截面的外半径。 烟囱发生二次前冲的前冲距离为 (13) 式中:L2为烟囱发生二次前冲的前冲距离。 由此得到烟囱倒塌前冲距离S的计算公式 烟囱水平触地或底部先触地 (14) 烟囱顶部先触地 (15) 某电厂待拆除烟囱为钢筋混凝土结构,高180 m,C40混凝土,HRB335级钢筋。标高0.00 m处,烟囱外半径8.335 m,壁厚0.5 m,无隔热层和内衬;标高12.90 m处,烟囱外半径7.561 m,壁厚0.5 m,隔热层厚0.06 m,内衬厚0.24 m;标高92.75 m处,烟囱外半径3.080 m,壁厚0.4 m,隔热层厚0.06 m,内衬厚0.12 m。竖筋为双层布筋,环筋为水平箍筋。标高12.90 m处外侧布设235根φ22竖筋,内侧布设58根φ16、60根φ14竖筋,环筋布置规格为φ18@200;标高92.75 m处外侧布设100根φ28竖向筋,内侧布设48根φ14竖筋,环筋布置规格为φ14@200。标高12.90 m至90.50 m范围内筒体自重4072.16 t,重心高度40.49 m。标高92.75 m以上筒体自重1410.45 t,重心高度132.21 m。 根据现场周边情况及相关资料,综合考虑爆破危害效应对周边环境影响,确定该烟囱采用分段定向控制爆破拆除。首先在烟囱上部开设高位爆破切口对上半段筒体实施定向爆破拆除,然后在底部开设爆破切口对下半段筒体实施定向爆破拆除。烟囱爆破切口参数见表1。 表 1 烟囱爆破切口参数 观察实际烟囱爆破过程(图5、图6)可知,烟囱倒塌过程主要分为两个部分。首先,爆破切口形成瞬间,烟囱在自身倾覆力矩作用下定向倒塌,爆破切口逐渐闭合,此过程伴随有筒体的下坐;当烟囱定向倒塌至一定角度时,筒体将脱离支撑部位发生前冲,直至触地解体破坏。这与理论分析结果相吻合。通过观察爆破倒塌视频可知:烟囱高位切口爆破拆除和下部切口爆破拆除前冲过程中均为烟囱顶部先触地,测量得到两次爆破筒体的下坐量均近似等于切口高度,且没发生明显后坐。 图 5 烟囱高位切口爆破倒塌过程Fig. 5 Chimney blasting collapse process with high incision 图 6 烟囱下部切口爆破倒塌过程Fig. 6 Chimney blasting collapse process with lower incision 3.3.1 前冲机理分析 根据烟囱自身结构和尺寸带入相关参数计算可得表2和图7结果,其中表2为两种不同判据条件下烟囱前冲倾角理论值与实测值统计表,图7为判据二条件下μ1与[θ]的关系曲线。由表2可得,在判据一和判据二(μ1=0.7时)条件下烟囱的前冲倾角近似相等,二者与实测值的误差在可接受的范围内,因此可认为这两种判据是合理的。但由图7可知,对于判据二前冲倾角[θ]会随着μ1的增加而增大,当μ1取较小值时,其与实测值的误差会增大。因此,当μ1值确定时,两种判据均可作为烟囱发生前冲时的力学依据,只是其分析原理不同,反之则采用判据一对烟囱的前冲进行判断。实际工程中,在设计时往往难于精确测定支撑部位的摩擦系数,因此将判据一作为烟囱发生前冲时的力学依据更为合理。 图 7 判据二条件下μ1与[θ]的关系曲线[18]Fig. 7 The relationship curve between the μ1 and [θ] under criterion 2[18] 3.3.2 前冲过程分析 在判据一条件下根据烟囱自身结构和尺寸带入相关参数计算可得表3结果,表3为烟囱前冲过程分析结果,其中下部切口的一次前冲距离为负值是因为筒体虽然发生前冲,但仍然处于烟囱自身的建筑限界之内;除此之外,由于在爆破拆除过程中采取了一系列的防冲措施,难于准确量测出筒体的二次前冲距离,因此烟囱的二次前冲距离仅有理论计算值。 由表3可得,烟囱前冲过程的理论分析结果与实测结果吻合较好,由此说明本文提出的前冲分析理论计算模型是合理的。两次爆破拆除烟囱倒塌范围S的理论值均大于实测值,是因为在实际爆破拆除过程中采取了铺设减振堤坝、防冲墙等一系列的防冲措施造成烟囱的二次前冲距离较小,这也说明该理论计算模型的计算结果偏于保守,可为类似工程提供参考。 研究表明,烟囱爆破拆除过程中塌落振动对周围建(构)筑物的危害最严重[13],且塌落触地振动速度不仅与塌落段烟囱的动能有关,还与烟囱倒塌过程中的触地姿态有关[5],而通过本文分析可知烟囱倒塌过程中的触地姿态影响着烟囱的前冲距离,进而影响着烟囱的塌落触地点,最终对塌落触地振动速度产生影响。因此,为进一步研究烟囱的触地姿态对塌落触地振动速度的影响,在前冲分析的基础上通过理论计算得出两次爆破拆除烟囱塌落触地振动速度的预报值,并与实测值进行对比,对理论模型的准确性和合理性进行验证。 根据建(构)筑物爆破拆除过程中的塌落振动速度计算公式[14] (16) 式中:vt为建(构)筑物塌落引起的地面振动速度;m为塌落段建(构)筑物的质量;Hc为塌落段建(构)筑物的重心下落高度;σ为材料的破坏强度;Rt为监测点到建(构)筑物触地冲击地面中心的距离;Kt、β分别为建(构)筑物塌落振动速度衰减系数和指数,分别取Kt=3.37~4.09,β= -1.66~-1.80。 大量烟囱爆破拆除塌落振动监测数据分析表明[14],当地面采取减振措施时,能保证烟囱的塌落振动速度减少70%。分别采用本文的方法对两次烟囱爆破拆除塌落触地振动速度进行理论计算,并与文献[21]的理论计算值进行对比,计算结果见表4。 表 2 不同判据烟囱前冲倾角理论值与实测值 表 3 烟囱前冲过程分析结果 表 4 烟囱爆破拆除塌落触地振动速度理论值 为确定烟囱爆破拆除对周围重点保护建(构)筑物的影响,起爆前分别在监测点1、2、3位置布置振动监测仪器对相应位置的振动进行监测。爆破结束后,将两次爆破拆除烟囱塌落触地振动速度监测值整理见表5。 表 5 烟囱爆破拆除塌落触地振动速度实测值 由表4和表5中的数据对比可知,在前冲分析的基础上,两次爆破拆除烟囱塌落触地点到监测点的距离Rt与实测值偏差较小,塌落触地振动速度与实际监测值吻合较好,而文献[21]中两次爆破拆除烟囱的Rt值与实测值存在差异,导致塌落触地振动速度与实际监测值差异较大。因此在实际工程中,应考虑烟囱的触地姿态对塌落触地振动速度的影响,在前冲分析的基础上研究烟囱的塌落触地振动更可靠。 结合力学理论分析了烟囱定向爆破倾倒过程和产生前冲的原因,在此基础上研究了烟囱的塌落触地振速。通过上述分析和讨论,得出以下结论: (1)当支撑部位的摩擦系数μ1值可精确测定时,N=0和F=0两种判据均可作为烟囱发生前冲时的力学依据,但二者分析原理不同,反之则采用判据一对烟囱的前冲进行判断。鉴于在实际爆破工程中难以获取精确的支撑部位的摩擦系数,将判据一作为烟囱发生前冲时的力学依据更合理。 (2)新建前冲距离计算公式的理论结果与现场实测结果吻合较好,采用此模型分析烟囱的前冲合理可行。在实际爆破拆除过程中采取了铺设减振堤坝、防冲墙等一系列的防冲措施,导致烟囱的二次前冲距离较小,出现倒塌范围的理论值略大于实测值的情况,表征该理论模型的计算结果偏保守,可为类似工程提供参考。 (3)烟囱爆破拆除过程中其塌落触地振动与烟囱的触地姿态有关。在前冲分析的基础上,两次爆破拆除烟囱的塌落触地振动速度与实际监测值基本吻合。因此在实际工程中,结合前冲分析对烟囱的塌落触地振动进行研究更可靠。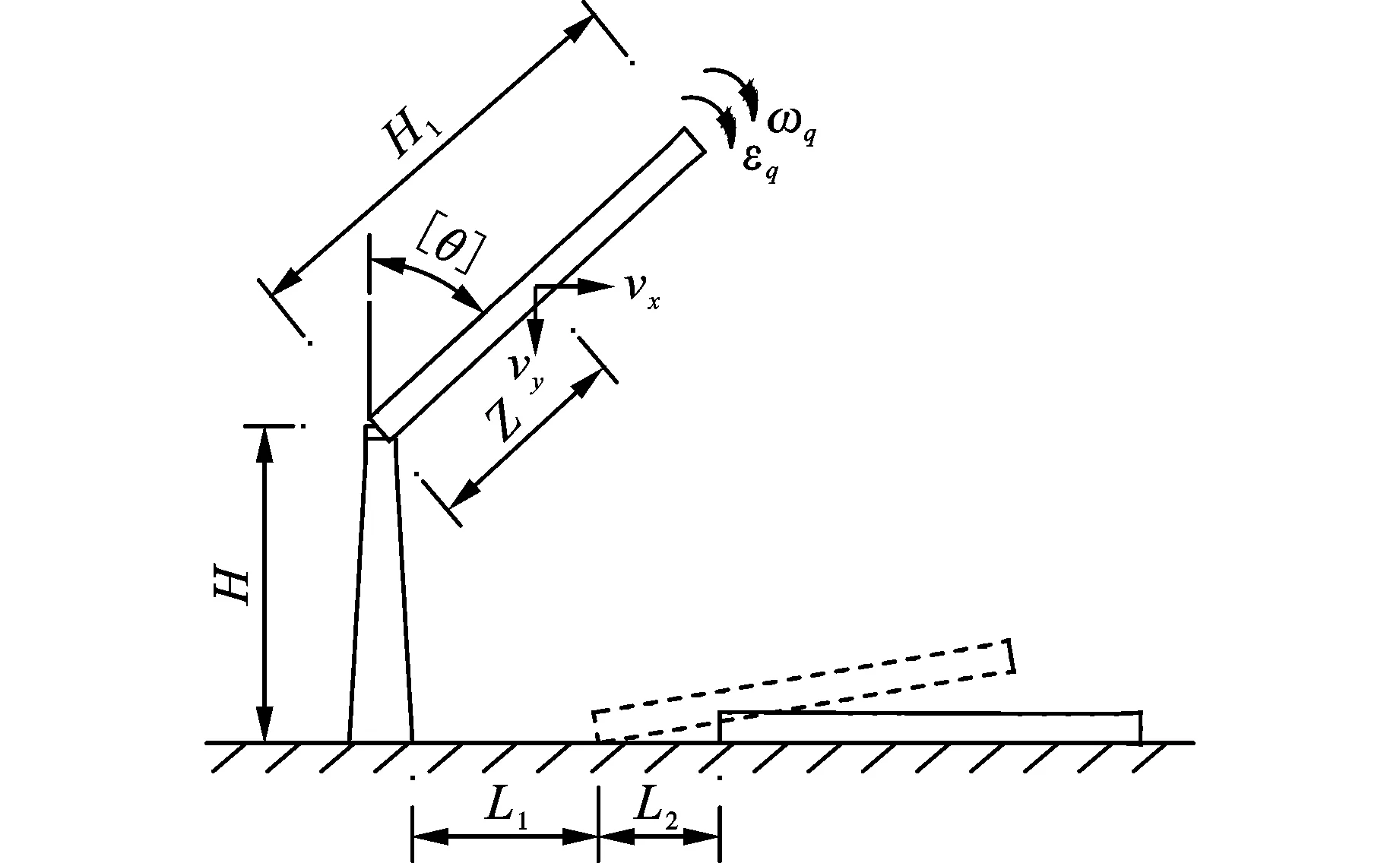


2.3 前冲距离计算
3 工程实例
3.1 工程概况

3.2 烟囱倒塌过程分析


3.3 前冲分析
4 烟囱爆破拆除塌落触地振动分析



5 结论

