圆形肋柱通道强化换热流动机理实验研究

段敬添 ，张 科,*，徐 进 ，雷 蒋 ，武俊梅

1.西安交通大学航天航空学院 机械结构强度与振动国家重点实验室，西安 710049

2.西安交通大学航天航空学院 陕西省先进飞行器服役环境与控制重点实验室，西安 710049

0 引 言

肋柱广泛应用于涡轮叶片内部的冷却通道，尤其是尾缘通道。一般认为，将肋柱安装于窄的冷却通道能够增加流体的润湿面积和湍流度，增强对流换热强度。此外，肋柱连接了压力面和吸力面，叶片结构强度也可以得到加强。

影响肋柱强化换热的因素很多，包括肋柱截面形状、肋柱阵列排布方式、通道几何形状和雷诺数等。研究[1-5]发现，在相同流动条件下，与顺排阵列相比，叉排阵列的总体换热系数较高，压力损失较大。在叉排通道中，Siw等[5]还观察到横向间距越大，通道壁面换热系数分布越均匀。Chyu等[6]利用瞬态液晶测温技术研究了肋柱高径比（H/D）对通道壁面换热系数分布的影响。结果表明，换热强化和摩擦系数均随H/D增大而增大，H/D=2.0的综合冷却特性最好。Chyu等[7]采用传质类比方法测量了圆形、方形和菱形肋柱窄通道的传质系数和压力损失，发现方形和菱形肋柱通道的整体平均传质系数高于圆形肋柱通道，而圆形肋柱通道的压力损失最小。Xu等[8]和Jin等[9]分别采用实验和数值模拟方法研究了肋柱截面形状对通道压力损失和传热特性的影响，发现NACA形、柳叶刀形截面肋柱的综合冷却特性优于圆形截面肋柱。在旋转工况下，Hung等[10]利用液晶示温方法研究了大小不均的肋柱交叉排布对通道传热特性的影响，观察到当插入较大尺寸的肋柱时，局部努塞尔数Nu和通道压力损失均增大。

毫无疑问，肋柱通道的换热特性和摩擦损失由内部流动结构决定。研究者对内部流场特性开展了大量研究。许相辉等[11]利用Tomo-PIV获得了圆形肋柱尾迹高分辨率的三维流场分布。王勇等[12]运用时间解析PIV研究了圆形肋柱绕流尾迹特性，发现肋柱后方1.9D位置附近两侧脱落涡交汇、掺混，湍流脉动最强。Marakkos等[13]利用PIV得到了固定于壁面的单根肋柱周围的速度场和涡量场分布，探究了马蹄涡系统的特性。Kirkil等[14]也研究了固定于平板的单根肋柱的马蹄涡特性，发现第一涡、第二涡和柱板交界处涡的随机性代表了肋柱阵列内部主要的流动特性。Xu等[3]利用微型PIV研究了顺排和叉排对微通道流场分布的影响，发现顺排通道中的流动转捩会引起涡脱落，从而导致横向流动，在交错排布通道中则未观察到流动转捩。在叉排通道中，Kannan等[15]使用大涡模拟方法研究了柱顶与壁面有/无间隙情况下的涡结构特征，观察到马蹄涡系统出现在每一根肋柱周围，且前两排马蹄涡强于后排。

研究肋柱阵列流动特征对于揭示其传热强化机理、指导叶片冷却构型设计至关重要。然而，目前针对传热和流动关联的研究十分不足。通常认为，肋柱附近的脱落涡会增强上游湍流度，破坏壁面的边界层[16-17]。Uzol等[18]采用液晶示温和PIV研究了双排圆形肋柱和椭圆形肋柱通道的传热特性和流动特性，发现通道中心线区域的湍流动能（Turbulent Kinetic Energy，TKE）与当地换热强度分布较为一致。Won等[19]测量了带肋柱矩形通道的努塞尔数Nu分布和流动结构，发现壁面上Nu最高的区域位于第一和第二马蹄涡正下方。Delibra等[20]采用数值方法得到了圆柱阵列的速度场、涡量场和温度场分布，研究表明：在远离壁面的区域，换热强弱主要受大尺度涡影响；壁面附近的区域，换热由小尺度的湍流脉动支配。Otto等[21]采用数值模拟和实验方法研究了圆柱阵列通道的Nu分布和流场分布，结果表明：随着雷诺数Re增大，尾迹区的闭合长度减小，剪切层内的湍流耗散加快。

以上研究主要关注于强换热区域的流动结构，仅对换热和流动进行了局部定性关联，对整个扰流通道内的流动特性分布尚不清楚，通道整体流动特性分布与换热特性分布之间的定量关联仍不明确。本文针对大宽高比通道内圆柱阵列的流动特性分布开展研究，并将其与努塞尔数Nu分布进行对比分析和定量关联。

1 实验装置

如图1所示，流场测量在一个封闭式水循环系统内进行。水从水箱内出发，流经泵、阀门、流量计、扩张段、发展段后进入实验段。实验段为宽高比RA= 4的矩形通道，通道中带有交错排布的圆形肋柱。带肋柱通道尺寸和布置与Xu等[8]的传热实验装置相同。

文献[22]表明叶片尾缘换热通道可近似为4∶1的矩形通道，肋柱高径比通常为0.5～4.0。本文采用高径比3.0的圆形肋柱。前人的研究表明，在叶片尾缘内部换热通道中，稀疏肋柱更有优势，本文采用流向间距4.5D、横向（垂直于流向）间距2.0D的稀疏肋柱。实验段上游扩张段由圆形逐渐过渡到矩形，圆形截面直径为28 mm，矩形通道的宽和高分别为W=100和H=25 mm（即矩形通道宽高比RA= 4）。扩张段之间布置阻尼网，减小来流脉动，使来流均匀稳定。从实验段进口下游510 mm（≈12.5Dh，Dh为通道的水力直径）处开始交错排布4排圆形肋柱，每根肋柱的直径为8 mm，高度与通道高度H相等（即肋柱高径比H/D≈3）。圆柱阵列排布如图2所示（图中定义流向为x方向，横向（垂直于流向）为y方向，坐标原点O位于第一排肋柱的中心），第一、三排分别布置6根完整的圆柱，第二、四排分别布置5根完整圆柱和2根半圆柱。

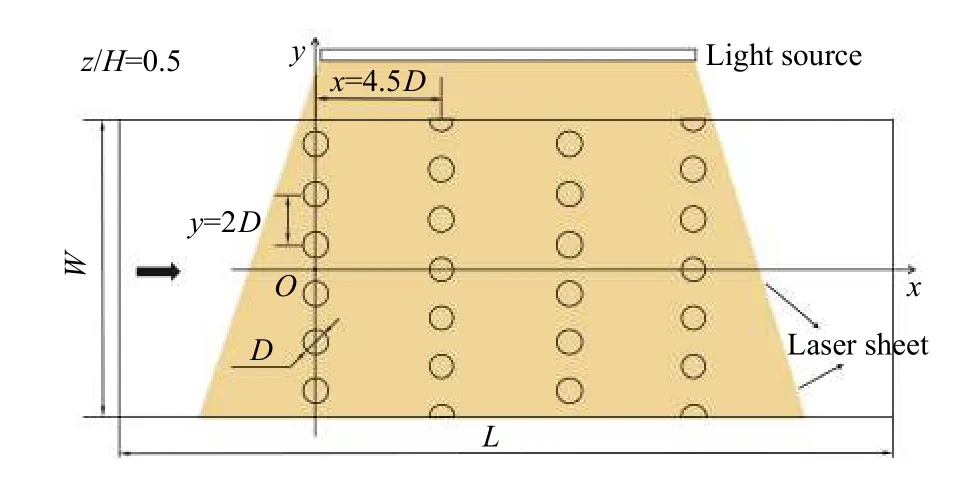
图2 测量区域圆柱阵列排布和尺寸说明示意图Fig.2 Orientation and dimension of pin fin array in the measurement domain

Otto等[21]的研究表明：在雷诺数Re较低的工况下，端壁附近的流动特性与通道中间平面相似（但湍流度较低）。因此，在Re=1.0×104和2.0×104条件下，本文采用激光粒子成像技术（PIV）测量通道高度方向中心截面（z/H=0.5）、x/D=–0.8～16.0之间的速度分布。Re=ubDh/ν，其中ub为通道内流体的平均速度（以涡轮流量计测量），Dh为通道的水力直径，ν为水的运动黏性系数。激光粒子成像技术（PIV）利用激光照射流体中均匀分布的示踪粒子，以相机记录相邻时刻示踪粒子的位移，进而计算得到流体瞬时速度分布。

在PIV实验中，以氧化铝（Al2O3）作为示踪粒子，均匀混合于水箱中。以波长532 nm的双脉冲Nd:YAG激光发射器产生激光片，从通道一侧射入，照亮测量平面，高速相机FASTCAM Mini AX从实验段正上方拍摄图像。激光发射器和高速相机由一个同步器控制，2个连续激光片或2次连续拍摄之间的时间间隔为400 ms（Re=1.0×104）和250 ms（Re=2.0×104）。PIV系统频率设置为2000 Hz，则速度测量频率为1000 Hz。基于快速傅里叶变换（FFT）的互相关理论，以MicroVec公司的MicroVec V3对2000对图片进行后处理，判读区域为16 pixel×16 pixel，50%重叠。经过后处理，可得到测量平面内每个位置（i,j）的1000个不同时刻k的瞬时速度（uk,vk）。其他与流动相关的物理量，如平均速度u、v，速度脉动强度urms、vrms以及湍流动能Kt等由以下方程结合（uk,vk）计算得到。

1）流向平均速度u、横向平均速度v

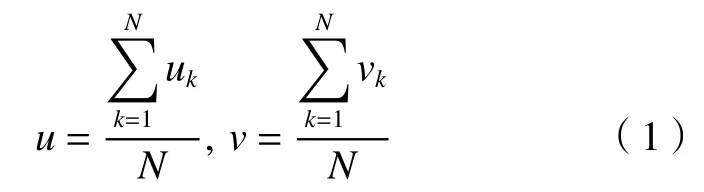
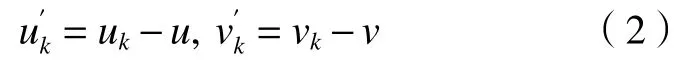
3）流向速度脉动强度urms、横向速度脉动强度vrms

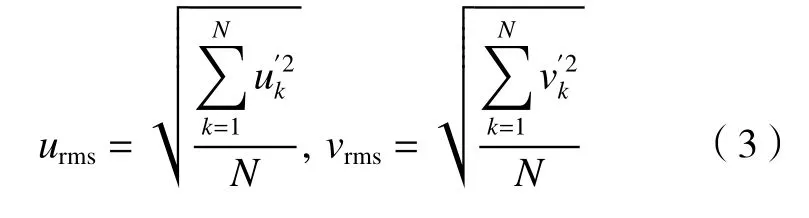
4）湍流动能Kt

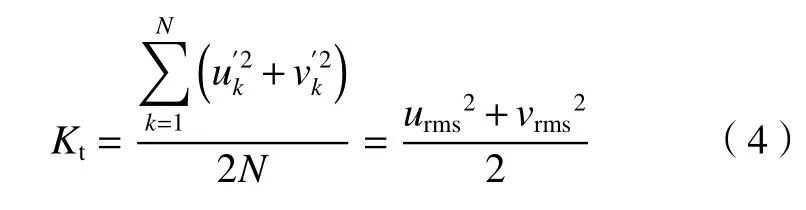
Xu等[8]以空气作为冷却流，并对端壁进行加热，使用热色液晶（Hallcrest公司，R40C20W）测量了相同通道结构、几何结构和雷诺数下的端壁内表面温度分布，经计算得到Nu分布。稳态液晶测温技术利用液晶颜色随温度变化的特性，以彩色相机记录稳态条件下喷涂液晶表面物体的颜色分布，实现壁面温度分布测量。热色液晶自身颜色与温度相关，测量之前需进行标定实验。当温度处在液晶显色范围之内时，液晶受热表面颜色发生变化，RGB相机记录不同温度下对应的标定板颜色，以此作为标准进行测量，便可得到被测表面的温度分布。关于传热实验和数据处理可参阅文献[8]。

2 结果与讨论

2.1 Nu分布与速度脉动场对比

为满足流动特性相似，传热实验和流动实验的Re保持一致。根据Dittus-Boelter公式，光滑通道参考努赛尔数Nu0=0.023Re0.8Pr0.4。此外，根据量纲分析，肋柱通道努赛尔数可表示为Nu=CRenPrm，其中C、m、n在特定情况下为常数。由于Re相同，水作工质的相对努赛尔数（Nu/Nu0）w和空气工质的相对努赛尔数（Nu/Nu0）a之间的关系为（Nu/Nu0）w=（Nu/Nu0）a（Pra/Prw）m－0.4。传热实验中Pra=0.7[8]，流动实验中Prw=0.9，二者均为常数，因此通道中（Nu/Nu0）w和（Nu/Nu0）a的比例为一常数。基于以上分析，本文假设空气工质的（Nu/Nu0）a与水作工质的（Nu/Nu0）w相似，讨论的传热结果也将基于空气工质的（Nu/Nu0）a。

图3展示了Re=1×104时的端壁Nu/Nu0分布以及通道中心平面的vrms和Kt分布（图中U0为通道中心截面来流进口的平均速度）。在传热实验中，受通道两侧壁面导热影响，通道底面靠近两侧壁面附近的温度比通道中间区域下降较大。本文主要讨论肋柱绕流导致的传热强化流动机理，不考虑通道底面靠近侧壁的传热数据。为与传热结果进行对比分析，流场结果展示区域与传热结果保持一致。从图3（a）可以看出：紧挨肋柱的上游区域与两侧传热有所增大。这些区域的传热强化由马蹄涡支配，其传热现象与Goldstein和Karni[23]以及Won等[19]的结果一致。

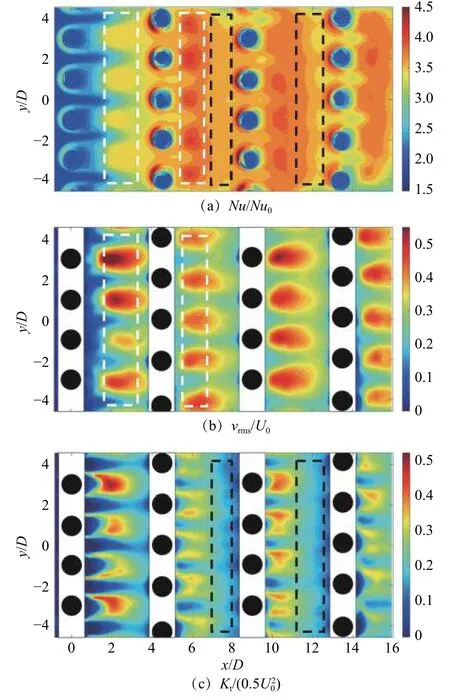
图3 Re =1×104时端壁Nu分布与测量平面内速度场统计量对比Fig.3 Comparison between Nusselt number distribution on the end wall and velocity field statistics in the measured plane for Re =1×104

从图3（a）还可以看出，肋柱强化换热主要发生于肋柱下游正后方大范围内，该范围的传热强化幅度与影响区域都非常大。Goldstein和Karni[23]以及Won等[19]将肋柱下游的传热强化与剪切层的再附联系起来。对比图3（a）和（b），可以发现第一、二排肋柱下游（尤其是白色虚线区域内）的Nu和vrms分布十分相似。具体而言，在回流区末端附近，Nu和vrms都出现了大幅度升高，在回流区内则有所降低，且两者的交界面沿横向是平坦的。Nu和vrms不仅分布相似，两者极值出现的位置也十分对应。这充分说明肋柱下游大范围的传热强化与肋柱下游横向速度脉动直接相关，而肋柱下游横向速度脉动应是由大尺寸涡脱落所引起。随着第二、三排肋柱下游流动的发展，肋柱回流区长度减小，较强的Nu和vrms区域前移，这些区域Nu和vrms的分布仍然相似。

作为对比，图3（c）给出了测量平面内的湍流动能分布云图。可以看出，在大部分区域，特别是高Nu分布区域，湍流动能分布和Nu分布并不吻合。除第一排肋柱下游外，湍流动能主要集中于肋柱两侧剪切层内，在第二、三排肋柱下游黑色虚线区域迅速变得均匀。相比之下，Nu在相应的剪切区域增强幅度并不大，Nu强化剧烈的区域主要在第一、二排肋柱正后方白色虚线区域内。这说明肋柱下游大范围传热强化更多来自于横向速度脉动，而剪切层内的小尺度脉动对传热强化贡献相对较弱。但是，如图3（a）黑色虚线内所示，在第二排和第三排下游更靠近其后排肋柱的区域，Nu分布比vrms更加均匀，和图3（c）黑色虚线内的湍流动能分布相似。

图4为Nu、Kt、vrms在x/D=6.0处沿y方向的变化曲线，其中Nu用被测表面最大值Numax进行归一无量纲化。可以看出，Nu和vrms在y方向上的分布以及峰谷位置非常一致，而Kt在Nu和vrms的峰值附近出现双峰。

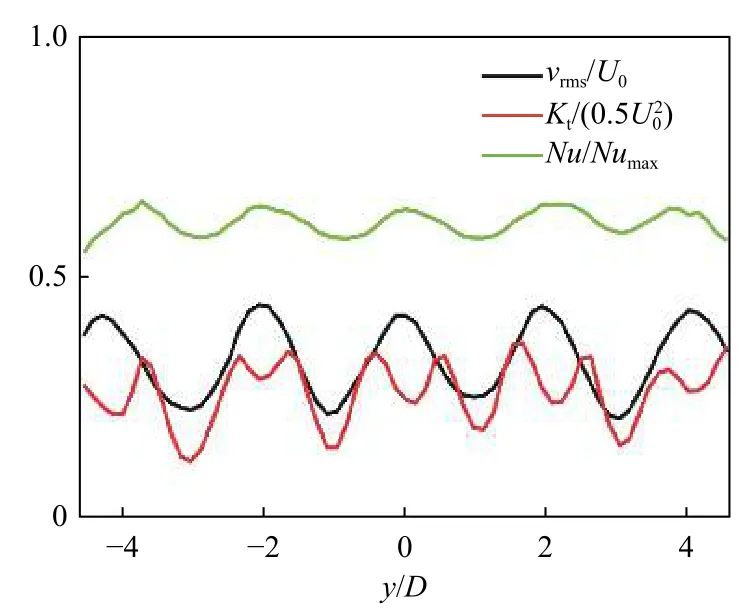
图4 Nu、Kt和vrms在x/D =6.0处沿y方向的变化曲线Fig.4 Variation of Nu, Kt and vrms along y at x/D =6.0

图5为x/D=6.0处Nu沿y向的分布与vrms及Kt沿y向分布的相关系数图。相关系数RNu,vrms与RNu,Kt的定义如下：

图5 Nu与vrms、Nu与Kt对应的相关系数曲线Fig.5 The corresponding correlation coefficient between Nu and vrms,Nu and Kt

以上相关系数分别表示该x位置Nu沿y向分布曲线与vrms沿y向分布曲线的相似性，以及Nu沿y向分布曲线与Kt沿y向分布曲线的相似性。从图5可以看出：零移位差时，Nu与vrms的相关性明显高于Nu与Kt的相关性，这说明传热强化分布与横向速度脉动强度变化更一致；而从图4也可以看到传热强化高的位置横向速度脉动强度大，两者一一对应，这说明传热强化与横向速度脉动存在直接关联。

以上讨论表明，圆形肋柱下游大幅度的局部换热强化主要和涡脱落引起的横向速度脉动相关，这可能是由于大的横向速度的冲刷作用极大地减小了壁面局部边界层厚度，使得局部热阻较小、换热增强，同时大尺度脉动也阻碍了当地边界层的发展，增强了换热[24]。然而，在图3（a）和（c）的黑色虚线区域内，Nu和Kt的分布较vrms分布更为均匀。

图6所示为Nu、Kt和vrms在x/D=7.5处沿y方向的变化曲线。可以看到，Nu/Numax沿y方向分布均匀，变化范围小于0.1，Kt的变化范围小于0.2。这些区域流动充分发展，肋柱排之间的换热和湍流动能分布更加均匀，说明在流动充分发展区域内，小尺度扰动起着均匀传热强化的作用。

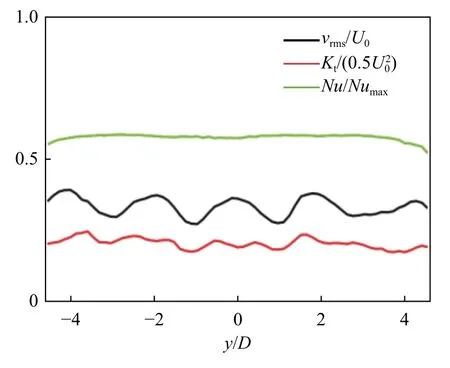
图6 Nu、Kt和vrms在x/D =7.5处沿y方向的变化曲线Fig.6 Variation of Nu, Kt and vrms along y at x/D =7.5

许多研究将Nu和Kt分布直接关联。然而，本研究发现，影响传热强化的因素并不只是湍流动能的增强。在流动发展过程中，由大尺度涡脱落引起的大幅度横向速度脉动是强化当地换热的主要流动因素。当流动充分发展后，小尺度脉动使传热分布更为均匀。

2.2 瞬时涡量分布

以上分析表明传热强化与横向速度脉动分布相似。本节聚焦单根肋柱下游局部速度与涡量分布及其演变，进一步说明肋柱下游流动结构与其演变，解释其对传热强化的作用。图7为第一排x/D=0、y/D=3.0处的肋柱下游涡量分布与速度向量在一个涡脱落周期内的变化（Re=1×104），其中Ωz表示z方向的涡量强度。从图中可以清晰地看到肋柱两侧剪切层在回流区下游x/D=1.6～3.0处（图中黑色虚线范围内）周期性脱落的大尺寸涡结构。在t =0～0.02 s、大尺寸顺时针涡向下游传递的过程中，可以看到肋柱下游x/D=2.5附近出现明显的向下速度，横向速度大小甚至和来流速度相当。而在t=0.03～0.05 s、逆时针涡向下游传递的过程中，可以看到肋柱下游x/D=2.5附近出现明显的向上速度。

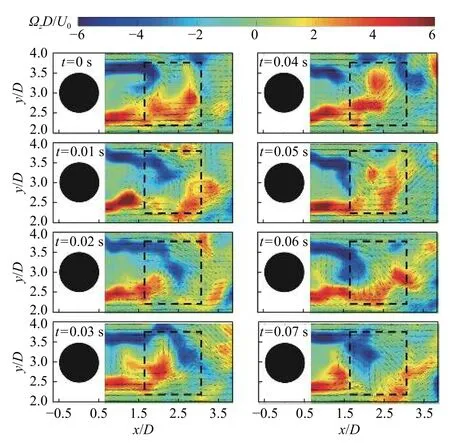
图7 Re =1×104时，第一排肋柱下游局部瞬时涡量分布Fig.7 Local instantaneous vorticity distribution with velocity vectors downstream of the 1st row for Re =1×104

图8和9分别给出了x/D=2.0、y/D=3.0处横向速度随时间的变化曲线及脉动能量频谱分布（Re=1×104），图9中Φ v’v’ 表示横向速度脉动的脉动能量。从横向速度随时间的变化曲线上看，可以发现涡脱落引起的横向速度最高可以达到来流速度的大小，且波动具有明显周期性。脉动能量频谱图展示了脉动能量的频率分布，从图中可以看到fD/U0≈0.32处有明显的突出峰值，说明横向速度脉动集中于这一特定频率，而这一频率正是肋柱尾迹涡脱落频率，这说明尾迹区下游强烈的横向速度波动是由肋柱涡脱落导致的。

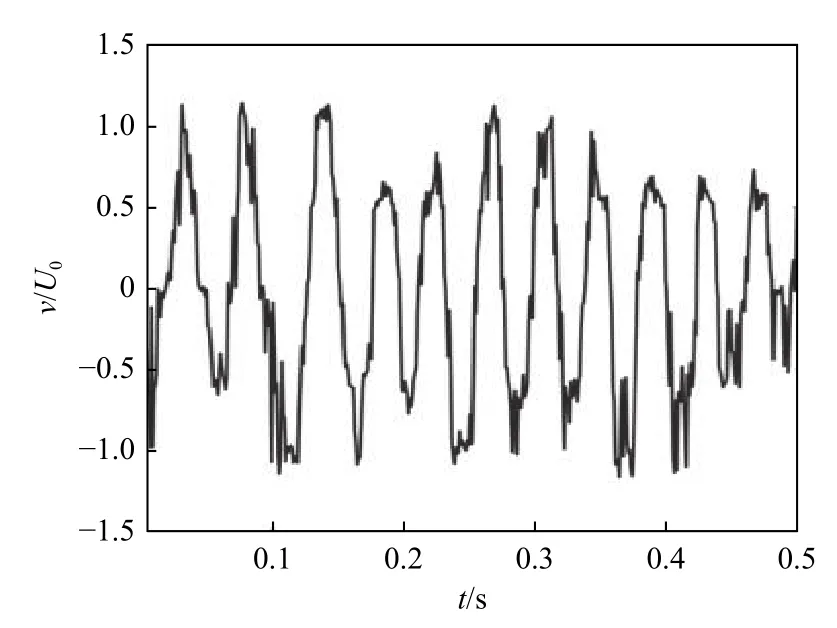
图8 Re =1×104时，x/D =2.0、y/D =3.0处的横向速度时间轨迹Fig.8 Time trace of the cross-stream velocity at x/D =2.0 and y/D =3.0 for Re =1×104

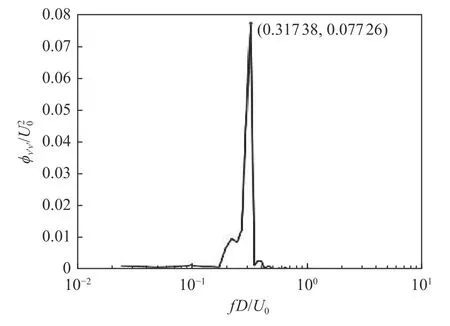
图9 Re =1×104时，x/D =2.0、y/D =3.0处的脉动能量频谱Fig.9 Power spectrum of the cross-stream velocity at x/D =2.0 and y/D =3.0 for Re =1×104

圆形肋柱下游周期性涡脱落与相应的速度脉动是研究者熟知的肋柱扰流中的流动现象。而在本文研究中，发现涡脱落与其诱导的横向速度高的区域（图7的黑色虚线区域）正好对应于肋柱下游换热大幅强化的区域（图3（a）的白色虚线区域），Nu和vrms分布相似度极大。有理由相信，涡脱落带来的强横向速度（或者横向冲刷作用）是圆形肋柱下游通道传热强化的主要原因；涡脱落带来的横向速度可以大大减小当地壁面边界层厚度，极大地提高当地对流换热系数。

作为对比，图10给出了第二排x/D=4.5、y/D=2.0处肋柱下游涡量分布与速度场演变图（Re=1×104）。可以看到，与第一排肋柱相比，第二排肋柱下游脱落涡尺寸更小，距离肋柱更近。因此，图3（a）中第二排肋柱下游局部传热强化的区域距离肋柱更近，位于x/D=6.0附近。同时可以看到，脱落涡在下游迅速被削弱破碎。

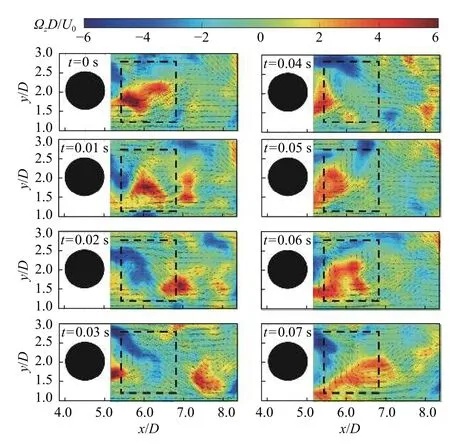
图10 Re =1×104时，第二排肋柱下游局部瞬时涡量分布Fig.10 Local instantaneous vorticity distribution with velocity vectors downstream of the 2nd row for Re =1×104

图11和12分别给出了x/D=7.5、y/D=2.0处（图3（a）的黑色虚线区域）横向速度随时间的变化曲线及脉动能量频谱图（Re=1×104）。可以看到，该处最大横向速度幅值相对第一排肋柱下游降低1/2，脉动能量分布不集中，同时出现小尺度高频（fD/U0>0.5）脉动能量。这说明流动向下游发展后，涡脱落尺寸减小，同时通道内小尺度脉动增强。因此，第二排肋柱下游局部传热强化区域较小，而涡脱落后小尺度脉动使传热分布更加均匀。

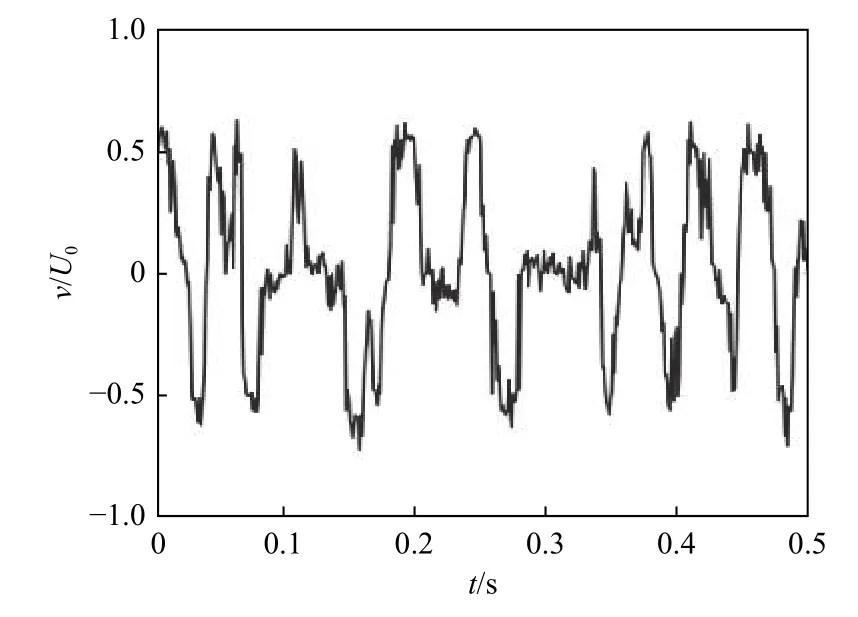
图11 Re =1×104时，x/D =7.5、y/D =2.0处的横向速度时间轨迹Fig.11 Time trace of the cross-stream velocity at x/D =7.5 and y/D =2.0 for Re =1×104

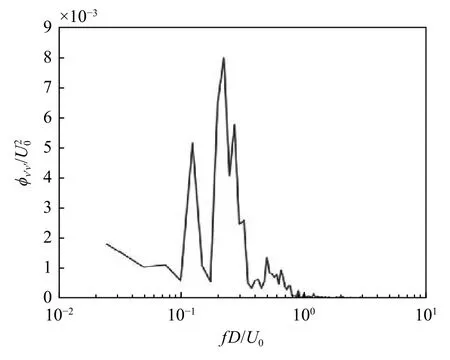
图12 Re =1×104时，x/D =7.5、y/D =2.0处的能量频谱Fig.12 Power spectrum of the cross-stream velocity at x/D =7.5 and y/D =2.0 for Re =1×104

2.3 Re的影响

当Re=2×104时，端壁Nu/Nu0分布和通道中心平面vrms和Kt的分布如图13所示。对比图3和13可以看出：当Re增大后，肋柱下游换热增强程度大幅度减弱，Nu/Nu0在较短的流动距离内趋于均匀；vrms也有相同的变化趋势，即横向脉动速度也随Re的增大而减小。但是，图13中的vrms和Nu分布和峰值位置仍然完全对应，说明涡脱落带来的横向速度波动仍然是局部传热强化的主要原因。

对比图7和14可以发现，当Re增大后，涡脱落尺寸减小、位置前移，诱导横向速度减小。说明当Re增大后，涡脱落强度减小，其引起的局部传热强化区域缩小、位置前移，同时强度减弱。而图13中Kt和Nu分布均匀的区域随Re的增大而扩大。说明当Re增大后，涡脱落之后的流动小尺度脉动占比增大，小尺度脉动使涡脱落之后的流场湍流动能与传热强化更加均匀。

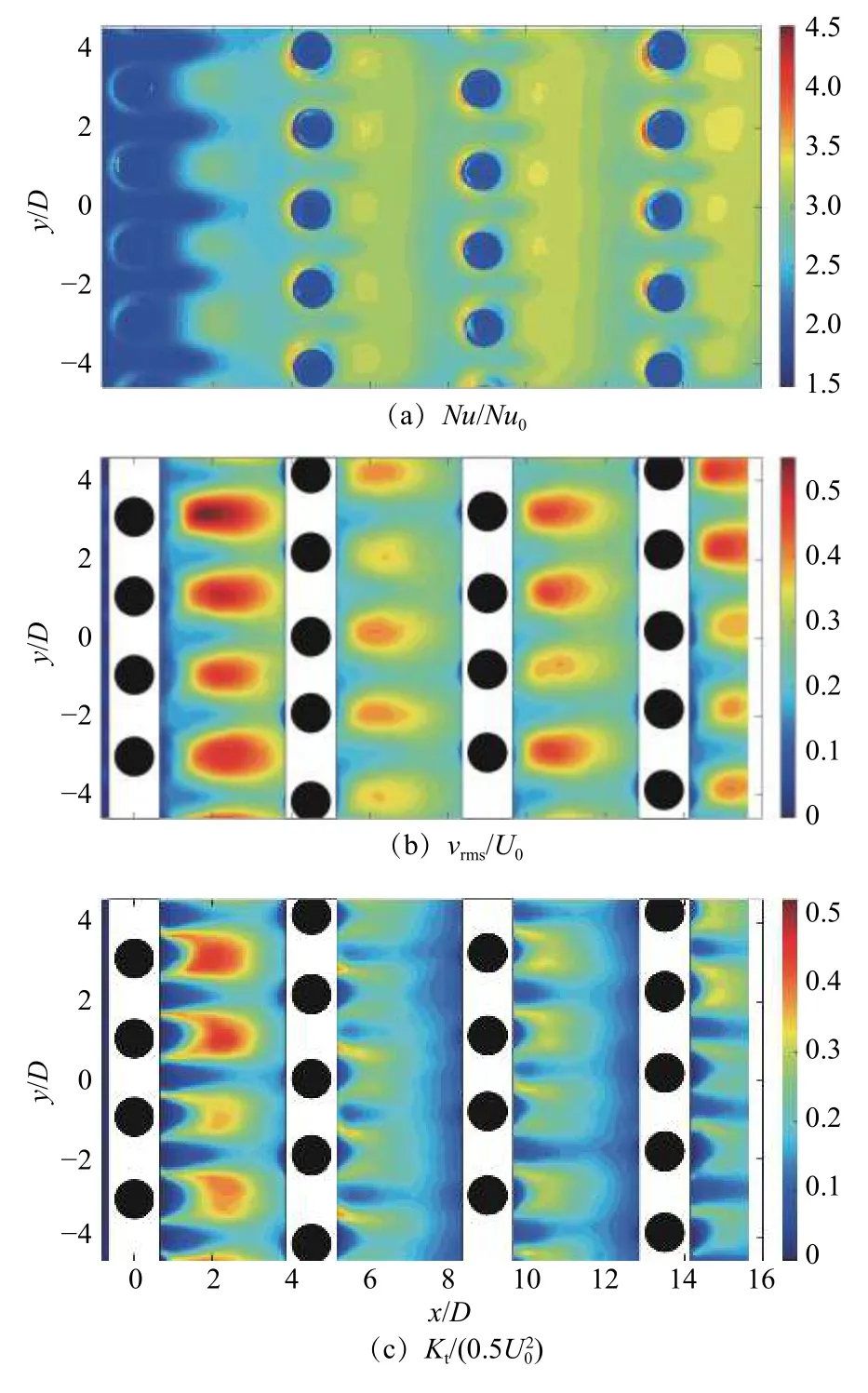
图13 Re =2×104时测量平面内的Nu, vrms和Kt分布Fig.13 The distributions of Nu, vrms and Kt in the measuring plane for Re =2×104

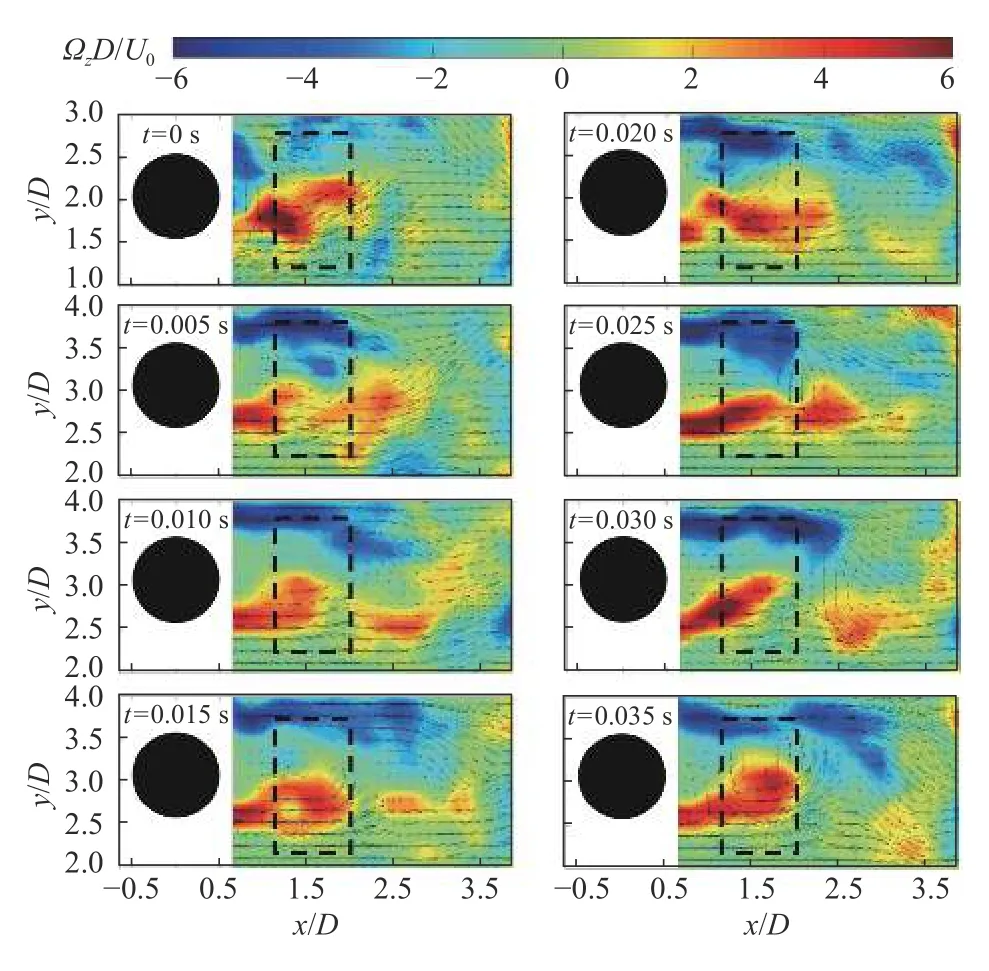
图14 Re =2×104时，第一排肋柱下游局部瞬时涡量分布Fig.14 Local instantaneous vorticity distribution with velocity vectors downstream of the 1st row for Re =2×104

需要再次说明：圆形肋柱下游大尺度涡脱落引起的强横向速度脉动是主导当地换热强化的主要因素，其引起的传热强化区域大、幅度强；涡脱落下游的小尺度脉动驱动当地传热强化，使得传热分布更为均匀。

3 结 论

利用PIV研究了圆形肋柱阵列矩形通道中间平面的流场特性，并与端壁的Nu分布进行了对比关联，得到了该通道中传热强化的主要流动机理。主要结论如下：

1）通过比较端壁上Nu分布和半高平面的流场分布特性，发现圆形肋柱回流区下游的Nu分布与vrms分布趋势非常相似，两者空间分布相关度极高。

2）从圆形肋柱回流区下游的流动发展与演变发现，肋柱下游大尺度涡脱落会导致大的横向速度分量，这种大范围大幅度的横向速度冲刷应该是当地局部换热强化的主要原因；而涡脱落下游区域的小尺度速度脉动占比增大，对该区域湍流动能与传热强化的均匀分布起到了关键作用。

3）圆形肋柱下游涡脱落与横向速度脉动均随Re的增大而减弱，端壁传热强化幅度也随Re的增大而大幅减弱。