汽车总装线的配置问题研究
崔亚 宋剑萍 韩晓东






摘要:本文围绕汽车总装线的装配问题,构建了以极小化生产成本为目标,以颜色等各个属性上的装配要求为约束条件的优化模型,并设计了基于贪心算法和遗传算法的新型混合算法,在matlab软件下编程求解,得到最优装配顺序。
Abstract: Focusing on the assembly problem of automobile final assembly line, an optimization model was built to minimize the production cost as the goal, and the assembly requirements on various attributes such as color as the constraint conditions. A new hybrid algorithm based on greedy algorithm and genetic algorithm was designed, which was solved by programming in MATLAB software to obtain the optimal assembly sequence.
關键词:优化模型;贪心算法;遗传算法;装配顺序
Key words: optimization model;greedy algorithm;genetic algorithm;assembly sequence
中图分类号:U471.23 文献标识码:A 文章编号:1674-957X(2021)17-0158-03
1 问题重述
汽车装配是汽车生产的一个重要环节,现有某汽车公司的装配流程图以及该企业一周的生产计划和每种型号汽车的品牌、配置、动力、驱动、颜色5种属性,现需根据装配要求使成本尽可能低的情况下,设计一个简单有效的算法将待装配车辆在总装线上重新进行排序。
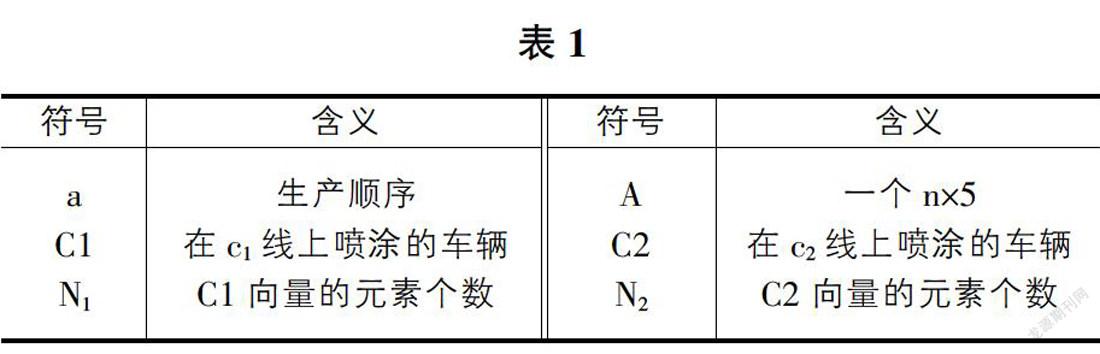
2 符号说明(表1)
3 问题分析
针对该问题,本文构建以极小化生产成本为目标,以颜色等各个属性上的装配要求为约束条件的数学优化模型。通过分析发现,贪心算法针对大规模问题很难获得最优解,故在求解上分为两步:首先使用贪心算法求解得到一个比较好的初值;然后运用遗传算法进一步改进,得到最终的最优装配顺序。
4 模型建立
本文运用线性约束和含有示性函数的约束条件来刻画生产中的限制条件,以生产成本最低为目标函数,构建了一个数学优化模型。将所有的示性函数转化为混合整数规划,形成一个大规模的混合整数的线性规划问题。
4.1 决策变量
设每天生产n辆车,其中一辆车有5种属性,就用一个n×5的矩阵把A所有车的信息表示出来。第一个属性取值为{1,2},分别对应品牌A1,A2;第二个属性取值可以为{1,2,3,4,5,6},分别对应配置B1,B2,B3,B4,B5,B6;第三个属性表示动力,取值为{1,2},分别对应汽油和柴油;第四个属性表示驱动,取值为{-1,1},分别对应两驱和四驱;第五个属性表示颜色,取值为{0,1,2,3,4,5,6,7,20}。则n×5的矩阵A表示如下:A=( )n×5。
此矩阵可用matlab软件生成。因为根据所给数据,已知每种车每天需要多少辆,例如9月17日,汽油、两驱,黄色的车要4辆。只需要把该属性的车对应的向量复制4次即可。程序为:,由此可生成矩阵A。
决策变量有两部分,第一部分是1×n维向量a,a中的元素是1到n的序号,代表生产顺序。例如a=(3,4,9,10,
6,5,…)代表先生产A中的第三行代表的车,然后生产第4行的,依次类推。第二部分是1×n维向量b,b中元素都为1或2,其中1代表在c1线上进行喷涂,2代表在c2线上进行喷涂。
根据以上所述可得决策变量为:
4.2 建立目标函数[1][2]
4.2.1 第一部分目标:降低车辆切换次数的成本
根据相邻两辆车之间的差异越大,成本越高,为了减少同一品牌下不同配置车辆之间切换次数的成本,故建立如下的目标函数,记为:
4.2.2 第二部分目标:降低喷涂线上更换颜料颜色的成本
设向量C1为在c1线上喷涂的车辆,C2为在c2线上喷涂的车辆,N1表示的是向量C1的元素个数,N2表示的是向量C2的元素个数。
因为有2条流水线,所以要识别出来每条流水线的车辆,就是把C1喷涂的那些车辆找出来,并把它们的序号记录下来。C1和a,b的关系是C1是b为1的那些a组成的向量。同理可得向量C2。例如a=(5,4,3,2,1),b=(1,1,1,2,2);那么C1=(5,4,3)。程序为:
为了使喷涂线上不同颜色的汽车之间切换次数尽可能少,分别建立以C1、C2两条线上颜色调换成本最小的目标函数如下:
其含义为:用向量的差或者向量部分分量的差来表示这种成本。
4.3 约束条件
由于工艺流程的制约和质量控制的需要以及降低成本的考虑,总装和喷涂作业对经过生产线车辆型号有多种要求:
4.3.1 装配要求
最多连续不超过2辆这个约束可以写成相邻2个且只有两个系数是1的线形约束,即在颜色之前的约束都可以用线性规划表示。综上所述,该项则需要细分为四个约束:
①四驱汽车连续装配数量不得超过2辆[3]。
②两批四驱汽车之间间隔的两驱汽车的数量至少是10辆。
③柴油汽车连续装配数量不得超过2辆。
④两批柴油汽车之间间隔的汽油汽车的数量至少10辆。
4.3.2 颜色要求
设颜色分别用数字0、1、2、3、4、5、6、7、20表示,如表2。
①黄与灰间隔。
②红与灰间隔。
③蓝与白间隔。
④金与红间隔。
⑤根据黑色汽车连续排列的数量在50-70辆之间,两批黑色汽车在总装线上需间隔至少20辆,可得:
4.3.3 通过引入辅助变量,我们将示性函数转化为混合整数约束
通过如上的转化技巧,可将所有的示性函数转化为混合整数规划约束。这样,就形成了一个大规模的混合整数的线性规划问题。
5 模型求解
5.1 模型算法
采用贪心算法结合遗传算法进行求解。首先使用贪心算法求解得到一个比较好的初值;然后运用遗传算法进一步改进,得到最终的的最优装配顺序。
5.2 模型求解实例
下面以求解9月20日的装配顺序为例,来介绍该模型的求解过程:
①考虑到1)每天白班和晚班都是按照先A1后A2的品牌顺序,装配当天两种品牌各一半数量的汽车;2)喷涂线上汽车颜色的要求;3)总装线上汽车颜色的要求,使用贪心算法得到一个汽车的装配顺序,即为初值向量。
②检验的最优性,利用matlab编写程序把生产汽车的数据生成矩阵,针对依然不满足的相邻班次衔接处的要求以及颜色的要求采用遗传算法进行调整,最终得到9月20日的最优装配顺序。
6 模型优缺点
6.1 模型的优点
新混合算法,一方面克服了贪心算法针对大规模问题难以获得全局最优解的不足,另一方面克服了遗传算法计算速度慢的不足,具有较好的实用价值。
6.2 模型的缺点
该混合算法相较贪心算法與遗传算法有了大幅的提升,但这两种算法都是人工智能算法,针对大规模问题找到最优解的速度很慢。
参考文献:
[1]孙文瑜,徐成贤,朱德通.最优化方法[M].第二版.高等教育出版社,2010.
[2]张可村,李换琴.工程优化方法及其应用[M].西安交通大学出版社,2007.
[3]刁在筠,刘桂真,戎晓霞,王光辉.运筹学[M].第四版.高等教育出版社,2016.
[4]Frank R. Giordano,William P.Fox,Steven B.Horton 著,叶其孝,姜启源 等 译. 数学建模(原书第5版),A First Course in Mathematical Modeling(Fifth Edition)[M]. 机械工业出版社,2014.

