基于LSTM模型的中国CO2排放量预测影响因素分析

赵雄飞 李远利

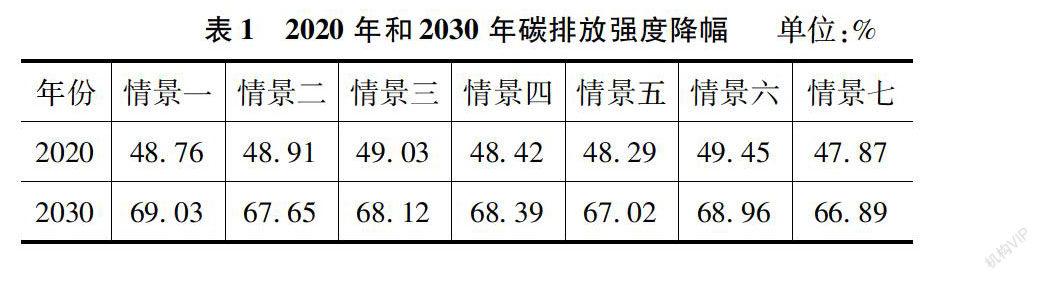
[摘 要]文章构建了基于LSTM的CO2排放量预测模型，利用中国1978—2016年的数据进行实证检验。为研究影响CO2排放量因素中的科技进步、产业结构及能源结构因素的组合效应，通过设定7种情景预测了2017—2030年的中国CO2排放量，并计算了2020年和2030年较2005年碳排放强度的降幅。结果表明：科技进步、产业结构和能源结构因素的变动能够大幅影响CO2的排放，三种因素组合减排的效果存在差异，且三种因素的叠加并非优于两种或一种因素带来的减排效果。

[关键词]CO2排放量;LSTM模型;组合效应;情景设定

[DOI]10.13939/j.cnki.zgsc.2021.22.015

1 问题的提出

近三十年来，中国的经济得到了飞速的发展，工业化和城市化进程的速度居于世界前列，而高速发展的背后很大程度上依赖于能源的巨大消费和高碳排放的基础，伴随着能源消耗产生的温室气体，特别是CO2被认为是导致全球气候变暖的主要因素，在此背景下，对CO2排放的研究则凸显得极其重要。虽然中国的经济正在飞速前进，但短期内中国依然是一个发展中国家，经济水平还不够高，因此在保持经济总量及能源消费持续增长和达到2020年CO2减排目标中如何控制相关影响因素的研究，就显得尤为重要。

2 文献综述

关于碳排放影响因素的研究已经受到国内外众多学者的关注，为顺应低碳经济的趋势，学者们尝试采用各种不同的方法研究碳排放与不同因素之间关系，以期找出节能减排和可持续发展的目标优化路径。目前关于CO2排放的方法使用上，取得较好成果的大体有环境库兹涅茨曲线（EKC）、指数分解分析方法（IDA）、投入产出法、KAYA等式及变形、计量经济学方法等五类。

关于CO2排放预测方法上，许多学者做出了大量的工作，主要分为两类，一类是单一建模预测方法，另一类是组合模型预测方法。现行的单一建模预测模型有STIRPAT模型、IPAT模型、灰度预测模型、神经网络模型等。相比其他模型，深度学习算法能够避开过多传统条件的限制，通过深度神经网络结构层挖掘变量之间潜在的非线性关系，从而提高对CO2未来排放量的预测精度。为了探寻影响CO2排放的多方面因素，选择深度学习模型中的LSTM神经网络预测模型。

3 CO2排放预测模型的构建

3.1  CO2排放量计算方法

采用碳排放系数法，碳排放系数法能够全面考察能源产业不同于化石燃料燃烧导致的温室气体排放，适用于各尺度的能源碳排放核算。文中对排放因子的选择采用中国全部省碳含量和平均低位发热量计算而来，这样更符合中国碳排放现实情况。

在计算碳排放过程中，由于煤炭、石油及天然气消耗总量占整个能源消耗的比重在90%左右，所以我们在碳排放计算过程中只计算这三种常用能源消费产生的碳排放情况。碳排放计算式为：

C=∑Ei×EFi×θi

式中：C为不同年份能源消费产生的碳排放总量，Ei为相应年份消费的第i种能源量，EFi为第i种能源的碳排放因子，θi为第i种能源消耗的氧化率。

3.2  LSTM预测模型

文章简要介绍LSTM神经网络模型，LSTM训练算法的总体框架主要包括：前向计算每个神经元的输出值;反向计算每个神经元误差σ的值，即采用BPTT算法进行计算;根据相应误差项，计算每个权重梯度。对于给定序列input=（x1， x2， …， xn），通过下列迭代式计算出h=（h1， h2， …， hn）和一个输出序列output=（y1， y2， …， yn）。

zt=tanh（Wzxt+Rzht-1+bz） it=σ（Wixt+Riyt-1+pi⊙ct-1+bi）

ft=σ（Wfxt+Rfht-1+pf⊙ct-1+bf） ct=it⊙zt+ft⊙ct-1

ot=σ（Woxt+Roht-1+po⊙ct+bo） ht=ot⊙tanh（ct）

xt和ht是LSTM連接层在t时刻的输入和输出。Wz、 Wi、 Wf和Wo分别为连接层输入、输入门、遗忘门和输出门的权重。Rz、 Ri、 Rf和Ro分别是连接层输入、输入门、遗忘门和输出门的循环层权重矩阵。bz、 bi、 bf和bo分别为连接层输入、输入门、遗忘门和输出门的偏置项。⊙为数组元素依次相乘。

3.3 变量选取及模型构建

结合过去学者研究总结，CO2排放的影响因素总结为科技、结构和规模等三个宏观因素，具体细分为经济规模、人口规模、城市化水平、科学技术、产业结构、能源消费结构、能源强度等七个微观因素。本文选择人均GDP、人口、机动车保有量、科技进步、能源强度、城市化率、产业结构和能源结构8个因素作为输入变量。

通过对上述所选8种影响因素的描述和分析，在构建LSTM神经网络模型时，将CO2排放量、人均GDP、人口、机动车保有量、科技进步、能源强度、城市化率、产业结构和能源结构9个变量都考虑作为神经网络的输入，考虑到样本量较少，同时也避免模型的拟合效果出现过拟合、欠拟合的情况，所构建的LSTM模型的隐含层个数和层神经元数分别为3、2。

3.4  精度检验指标

实验采用的常规误差评价指标主要有绝对误差百分比（MAPE）和均方根误差（RMSE），其中RMSE表示各期实际观察值与各期预测值的平均误差水平，两指标值越小模型误差精度越好。yi为第i年的实际CO2排放量，i为第i年CO2排放量的预测值。

MAPE=1N∑Ni=1yi-iyi RMSE=1N∑Ni=1（yi-i）2

4 模型构建

4.1 数据说明

文章从国家统计局、《中国统计年鉴》和OECD数据库中选取1978—2016年所选影响因素的相关数据。其中人均GDP是以1978年为基期计算的实际GDP除以总人口得到的;科技进步是以每年R&D支出与当年财政总支出的比求得，由于1978—1990年统计年鉴中缺少R&D支出项，因此选用有关科技的财政支出项代替;产业结构选用第二产业增加值占国民生产总值的比重表示;能源结构用煤炭消费量占能源消费总量的比例表示;能源强度的计算由每年的能源消耗总量与以1978年为基期求得的实际GDP的比值得到。