新型钢束柱体系的稳定性能研究

王庆贺,王仕奇,陈 宇,张龙巍

(1.沈阳建筑大学土木工程学院,辽宁 沈阳 110168;2.沈阳建筑大学建筑与规划学院,辽宁 沈阳 110168)

模块化建筑运用图解生成与转换设计的方式分析建筑原型,通过合理的模数控制对建筑原型进行标准化和规格化分解,形成标准化杆件、连接节点以及构成模块,通过对部件的叠加及转化形成结构模块[1]。装配式钢结构可采用格构柱,将多根单肢柱通过缀条或缀板连接。模块化装配式钢结构作为一种高度工业化的建筑,结合了模块化建筑及装配式钢结构的设计思路,具有施工效率高、安全性强及质量好等优点[2-3]。工程应用中,钢结构格构柱所受荷载方向与主轴有一定偏离,使构件处于双向压弯状态。因此,解决构件在双向压弯状态下的稳定问题是保证工程质量的关键。鹿翰[4]分析了长细比、分肢间距等因素对双肢格构柱稳定性的影响,得到各因素对双肢格构柱稳定性的影响规律:随长细比及分肢间距的增大,双肢格构柱的稳定性降低;通过对不同角度布置下格构柱的用钢量及临界荷载进行分析,认为缀条与单肢柱轴线的合理夹角为40°～55°。杨有福等[5-7]针对三肢钢管格构柱的极限承载力及抗震性能进行了研究,将试验结果及规范结果进行对比,发现随着单肢柱钢管壁厚的增加,构件承载力及初始刚度逐渐增大,规范公式计算结果偏于安全。柯晓军等[8-13]对四肢钢管格构柱在压弯条件下的稳定问题进行分析,在考虑几何和材料非线性的基础上,研究了初弯曲对构件稳定性的影响,认为初弯曲为构件长度的0.1%时,稳定承载力下降约10%,之后每增加0.1%,稳定承载力下降约5%。杨应华[14]等对压弯状态下四肢钢管混凝土格构柱的稳定性进行分析,得到偏心距、偏心率等因素对四肢格构柱稳定性的影响规律:随偏心距、偏心率增大,四肢格构柱的稳定性降低。目前,针对钢束柱体系稳定性的研究尚未见到报道,且现有的钢结构规范或规程的计算方法不能直接用于钢束柱体系的稳定性计算。

基于此,笔者提出四肢及六肢钢束柱稳定性及最不利荷载角的计算方法。分析弦板用钢量相同时,弦板间距、计算长度、荷载偏心距、荷载角对四肢及六肢钢束柱的整体稳定性及单肢柱稳定性的影响规律,量化各因素对钢束柱体系稳定性的影响幅度,为相关工程应用提供参考依据。

1 钢束柱稳定性理论分析

1.1 钢束柱体系设计

基于模块化钢结构建筑理念,笔者提出了一种新型钢束柱体系如图1所示。该体系包括多根单肢柱、法兰紧固盘及接榫梁等组件。其中单肢柱作为竖向受力构件,由上旋柱、连接柱、下旋柱构成,上、下旋柱通过连接柱成为整体,束柱加固弦板可以提高构件的抗剪能力,接榫梁为横向受力构件。法兰紧固盘作为核心的连接转换部件,固盘内部设置均质的柱孔,可以根据不同空间和承载需要,将不同数量的单肢柱及接榫梁通过榫卯锁连接。钢束柱体系可塑性强,当作用于钢束柱体系上的荷载发生变化时,可通过对梁柱系统的调配和法兰紧固盘的叠加布置,为钢束柱体系提供多种连接方式,从而提高钢束柱体系的精确性及高效性。钢束柱体系采用自锁式构造,可避免实体单元的柱体向杆件模块化过程中受到单量度的限制,进而通过杆件的阵列形成一定的空间体系,因此相对于传统的实体单元,阵列化杆件更显轻盈,更具空间视觉转化性。

图1 钢束柱体系设计及组成分析

1.2 钢束柱体系及单肢柱的稳定性分析

钢束柱体系的实际受力状态复杂,笔者基于其典型的受力形式提出稳定性计算方法。法兰紧固盘作为核心连接部件,可以抵抗轴向压力、弯矩、剪力及局部挤压力,因此将法兰紧固盘视作固定端,钢束柱体系采取两端固定的边界条件。钢束柱体系采用弦板与法兰紧固盘共同加强单肢柱的整体性,在分析单肢柱稳定性时,计算长度取相邻弦板间净距。钢束柱体系的稳定性采用边缘屈服准则,构件的应力变化服从线弹性规律,不考虑截面塑性发展。钢束柱体系的应力为

(1)

式中:σ为构件截面边缘处的正应力;A为构件的截面面积;N为构件的轴向压力;Mx、My为作用在构件主轴方向的弯矩;Wx、Wy为弹性截面模量。

考虑荷载初偏心时,钢束柱体系受到沿杆轴线的轴力和绕截面两个形心主轴方向的弯矩,结构处于双向压弯状态。钢束柱体系的整体稳定性采用《钢结构设计标准》(GB 50017—2017)中规定双向压弯构件的计算方法:

(2)

(3)

式中:λx为构件对x轴的长细比；λ1为单肢柱对最小刚度轴的长细比,计算长度取相邻弦板间的净距。

荷载角指荷载作用点与截面形心连线和截面形心轴的正向夹角[12]。当荷载的作用点与截面形心主轴的角度达到最不利荷载角时,钢束柱体系易发生压弯失稳。针对式(2)中关于荷载角θ的项数进行求导,得到钢束柱体系的最不利荷载角的计算方法:

(4)

单肢柱处于双向压弯状态时,构件会因受力过大进而丧失稳定性。单肢柱的稳定性检验采用《钢结构设计标准》(GB50017—2017)中规定双向压弯圆管的计算方法:

(5)

单肢柱数量增多可以增强束柱体系的稳定性,但同时导致用钢量增加,经济性降低。为此,笔者设计了4种新型构件,分别采用环形弦板的四肢及六肢钢束柱体系、矩形弦板的四肢及六肢钢束柱体系,量化单肢柱数量及弦板形式对钢束柱体系及单肢柱稳定性的影响。

1.3 四肢钢束柱体系的稳定分析

1.3.1 采用矩形弦板的四肢钢束柱体系

四肢钢束柱体系采用矩形弦板时,构件以虚轴作为弯曲轴。为增强钢束柱体系的整体性能,使主轴方向单肢柱间距相等。此时,各单肢柱至主轴的距离相同,即L=B。构件的形式如图2所示。

图2 采用矩形弦板的四肢钢束柱

钢束柱体系及单肢柱的应力分布服从线弹性规律,图3为四肢钢束柱体系的外力分布及单肢柱受力情况。

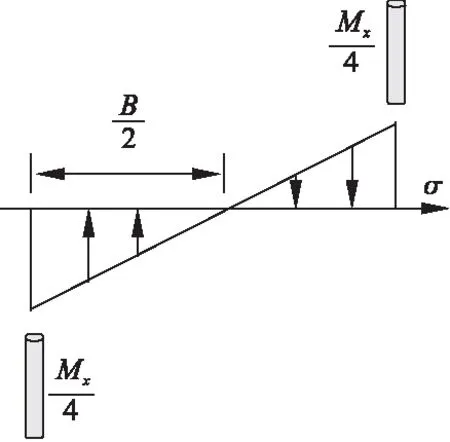
图3 四肢钢束柱的应力分析

此时,作用在单肢柱上的轴向压力为N/4、弯矩为M/4。其中M为荷载初偏心产生的附加弯矩。基于此,可以得到四肢钢束柱体系的单肢柱稳定性计算方法:

(6)

式中:d为单肢柱的直径。

由此可知,作用在单肢柱上的力与荷载角取值无关,单肢柱的稳定性与荷载角无关。

构件在弯矩作用平面内对受压最大纤维的毛截面模量W1x=W1y相同,得到四肢钢束柱体系的最不利荷载角为

(7)

1.3.2 采用环形弦板的四肢钢束柱体系

四肢钢束柱体系采用环形弦板时,构件的形式如图4所示。构件的受力情况与采用矩形弦板的四肢钢束柱一致,可按照边缘屈服准则及线弹性规律的基本原则对该构件整体稳定性和单肢柱的稳定性进行分析。当采用的环形及矩形弦板的用钢量相同时,采用矩形弦板的四肢钢束柱体系对主轴的弹性抗弯模量大,具有更好的抗弯性能,而两种体系中单肢柱的稳定性是一致的,均可采用式(6)进行计算。

图4 采用环形弦板的四肢钢束柱

1.4 六肢钢束柱体系的稳定分析

1.4.1 采用矩形弦板的六肢钢束柱体系

采用矩形弦板的六肢钢束柱体系的受力状态较四肢钢束柱体系复杂,构件以虚轴及实轴作为弯曲轴。此时,构件主轴方向上的单肢柱间距相等即L=2B。构件的形式如图5所示。

图5 采用矩形弦板的六肢钢束柱

该束柱体系在双向压弯状态下的外力分布及单肢柱受力情况如图6所示。该束柱体系的受力特点为实轴上两根单肢柱仅承受实轴方向的弯矩,作用在虚轴的弯矩由顶点的四根单肢柱承担,实轴上单肢柱用Z1表示,顶点的单肢柱用Z2表示。得到各单肢柱的受力情况如表1所示。

图6 采用矩形弦板的六肢钢束柱的应力分析

表1 各单肢柱受力分析

基于此,可以得到采用矩形弦板时,六肢钢束柱体系的单肢柱稳定性计算方法:

(8)

当矩形加固弦板的长为宽的2倍时,W1x=4/3W1y。该束柱体系的最不利荷载角为

(9)

分析式(8)可知,当荷载角θ=90°时,单肢柱的稳定性最差。

1.4.2 采用环形弦板的六肢钢束柱体系

六肢钢束柱体系采用直径为D的环形弦板时,构件在虚轴上的受力情况与采用矩形弦板的六肢钢束柱一致,构件形式如图7所示。

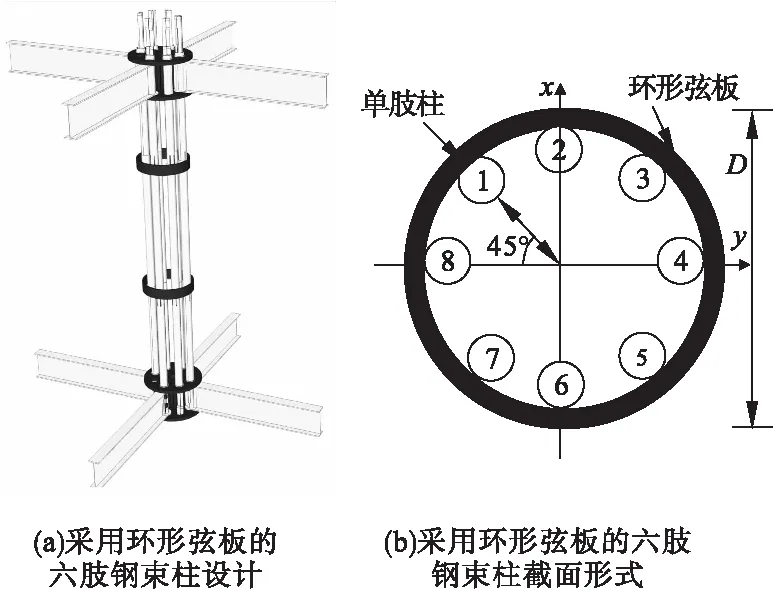
图7 采用环形弦板的六肢钢束柱

图8为该束柱体系在主轴方向的外力分布及单肢柱受力情况。该束柱体系中,实轴上的2个单肢柱受力大小相同,四角上4个单肢柱的受力大小亦相同。实轴上单肢柱用Z3表示,四角上的单肢柱用Z4表示,各单肢柱的受力分析如表1所示。笔者通过分析荷载角变化时,各单肢柱的受力大小进行单肢柱的稳定性计算。当荷载角θ=40.89°时,各单肢柱的受力大小相同;当荷载角θ<40.89°时,实轴上2个单肢柱所受弯矩较大,选取实轴上单肢柱进行稳定性计算;当荷载角θ>40.89°时,四角上的4个单肢柱所受弯矩较大。选取四角上的单肢柱进行稳定性计算,基于此,可以得到采用环形弦板时,六肢钢束柱体系的单肢柱稳定性计算方法:

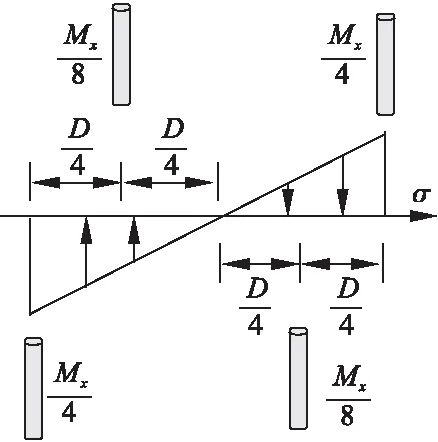
图8 采用环形弦板的六肢钢束柱的应力分析

(10)

(11)

构件中受力最大的单肢柱随荷载角的不同而变化,因此,单肢柱存在两个最不利荷载角。当θ<40.89°时,单肢柱的最不利荷载角为0°,当荷载角θ>40.89°时,单肢柱的最不利荷载角为90°,荷载角θ为40.89°时,单肢柱的稳定性最好。

2 钢束柱稳定性影响因素分析

笔者选取的钢束柱体系稳定性参数包括弦板间距、计算长度、荷载偏心距、荷载角[11-13]。利用所分析的计算方法量化双向压弯状态下各参数对钢束柱体系及单肢柱稳定性的影响规律。采用环形弦板的四肢及六肢钢束柱体系用S1、S3表示,采用矩形弦板的四肢及六肢钢束柱体系用S2、S4表示。工程中四肢格构柱常用的矩形缀板尺寸为500～600 mm[14];基于此,四肢钢束柱体系采用的矩形弦板长度L及宽度B均取550 mm,在保证弦板用钢量相同的前提下,单肢柱直径d取100 mm、环形弦板直径D取700 mm、六肢钢束柱体系采用的矩形弦板长度l取740 mm、宽度d取370 mm。在保证弦板稳定及构件刚度的情况下,钢材强度fy取235 MPa、弦板间距Δh取700～3 700 mm、计算长度l取3.0～4.5 m、荷载偏心距e0取0.1～0.4 m、偏心力N取200 kN、荷载角θ取0°～90°,构件的稳定性能用σ/fy表示。

2.1 弦板间距

图9为弦板间距Δh对钢束柱体系及单肢柱的稳定性影响规律。可以看出,弦板间距对钢束柱体系及单肢柱的稳定性影响较大,当钢束柱体系的计算长度一定时,应限制弦板间距。当弦板间距较大时,单肢柱的长细比较大,在钢束柱体系失稳之前单肢柱先发生失稳,当弦板间距较小时,增加弦板的数量对提高单肢柱的稳定性不明显。以采用环形弦板的六肢钢束柱体系为例,弦板间距Δh由2 700 mm减小至1 700 mm时钢束柱体系稳定性提高11.80%,单肢柱稳定性提高3.32%;弦板间距Δh由1 700 mm减小至700 mm时钢束柱体系的稳定性提高6.58%,单肢柱的稳定性提高1.80%。

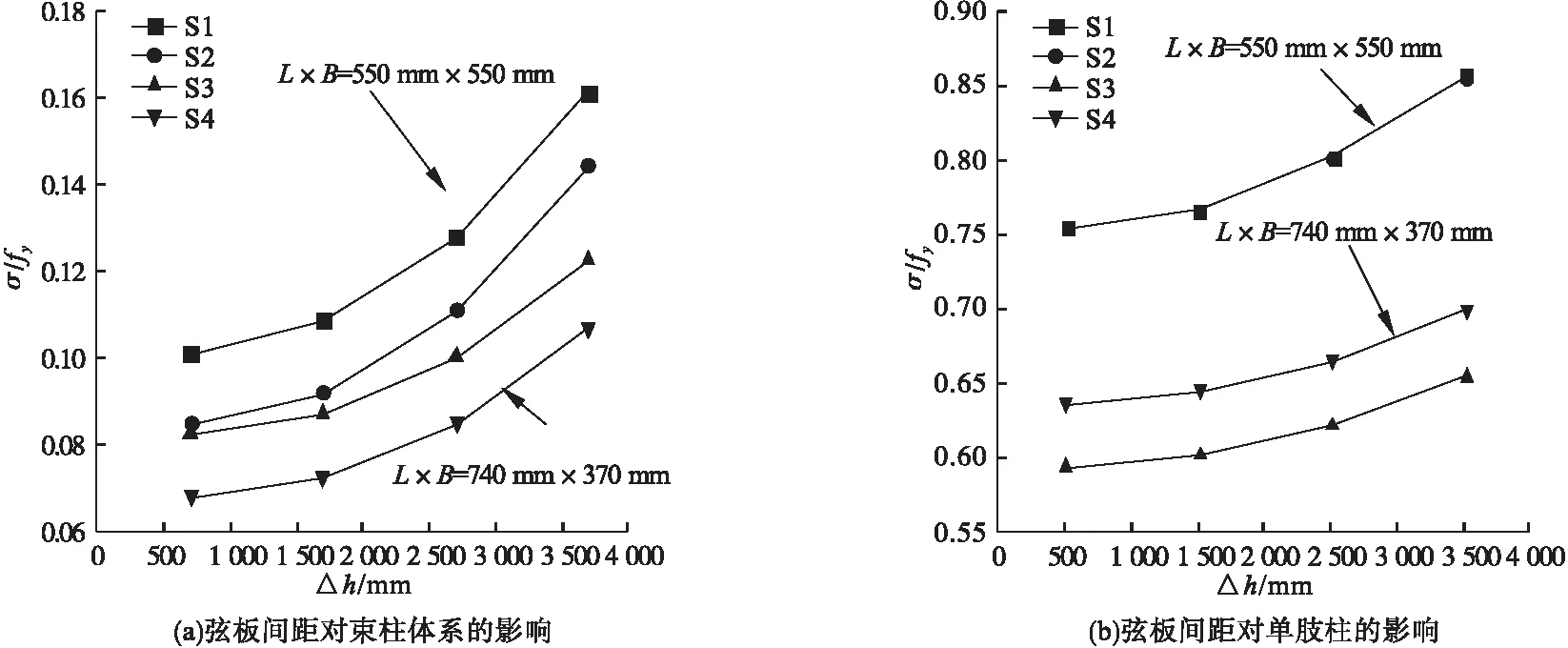
图9 弦板间距的影响

2.2 计算长度

图10为计算长度l对钢束柱体系及单肢柱的稳定性影响规律。由图10可知,钢束柱体系的稳定性随计算长度增加而降低,但不影响单肢柱的稳定性。这是由于随着计算长度的增加,换算长细比增大,二阶效应对构件稳定性的影响逐渐显著,构件趋向失稳破坏,而计算单肢柱稳定性所采用的长细比取决于弦板间距。以采用环形弦板的六肢钢束柱为例,当计算长度l由3.0 m增加至3.5 m时,钢束柱体系的稳定性降低22.06%,计算长度l由3.5 m增加至4.0 m时,钢束柱体系的稳定性降低35.69%。

图10 计算长度的影响

2.3 荷载偏心距

图11为荷载偏心距e0对钢束柱体系及单肢柱的稳定性影响规律,构件的稳定性随荷载偏心距的增加而降低,且偏心距越大,构件稳定性的下降幅度越大。以采用环形弦板的六肢钢束柱体系为例,荷载偏心距e0由0.1 m增至0.2 m时,构件的稳定性降低4.26%;荷载偏心距eo由0.2 m增至0.3 m时,构件的稳定性降低20.93%。

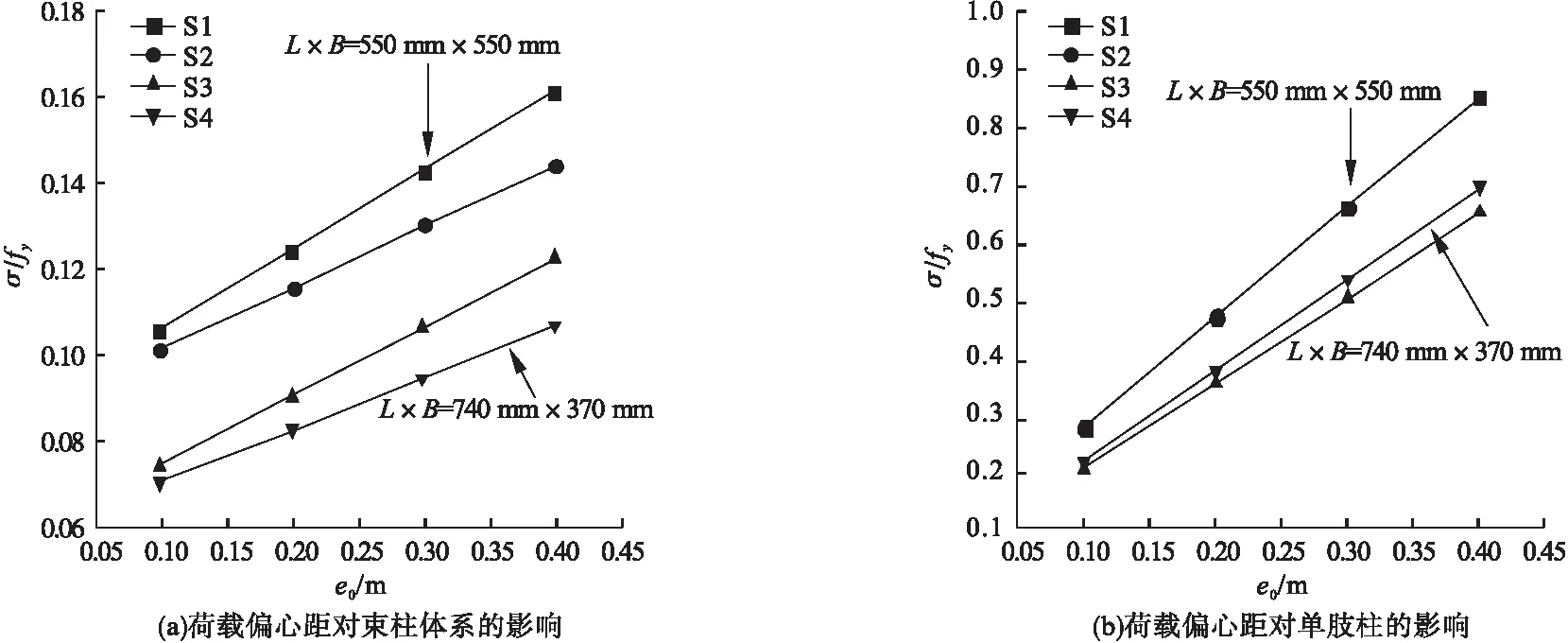
图11 荷载偏心距的影响

2.4 荷载角

图12为荷载角θ对钢束柱体系及单肢柱的稳定性影响规律,钢束柱体系的稳定性随荷载角θ增大呈现先减后增的趋势,四肢钢束柱体系中的单肢柱的稳定性不受荷载角的影响。六肢钢束柱体系采用环形弦板时,单肢柱的稳定性随荷载角θ增大呈现先增后减的趋势;而采用矩形弦板时,单肢柱的稳定性随荷载角θ增大而不断降低。当荷载角θ=36.7°时,两种体系的单肢柱稳定性相同;当荷载角θ<36.7°时,采用矩形弦板的束柱体系的单柱稳定性较好;当荷载角θ>36.7°时,采用环形弦板的束柱体系的单肢柱稳定性较好。

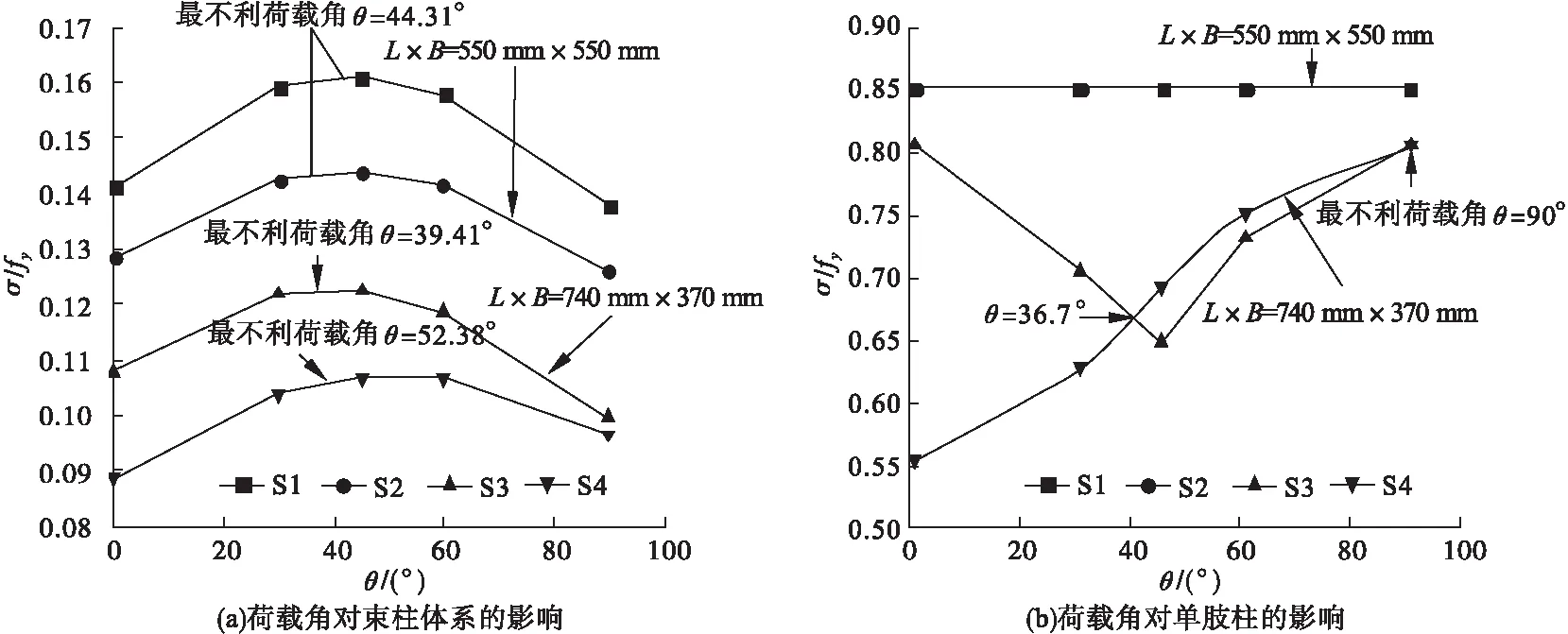
图12 荷载角的影响

3 结 论

(1)双向压弯状态下,六肢钢束柱体系的稳定性优于四肢钢束柱体系,相较于采用环形弦板的束柱体系,钢束柱体系采用矩形弦板的稳定性更好。

(2)推导了钢束柱体系的单肢柱稳定性及最不利荷载角的计算方法,当荷载角θ>36.7°时,采用环形弦板的束柱体系的单肢柱具有更好的稳定性。

(3)钢束柱体系及单肢柱的稳定性随弦板间距、荷载偏心距减小而增强,钢束柱体系稳定性随计算长度的增加而降低,随荷载角θ增大呈现先减后增的趋势。