工字形曲线组合梁负弯矩区侧向失稳分析

陈百玲,李明姝,刘文文,王连广

(东北大学资源与土木工程学院,辽宁 沈阳 110819)

曲线钢与混凝土组合梁是一种采用抗剪连接件将混凝土板与弯曲钢梁连接在一起的新型结构形式[1],它能充分发挥结构各自的优点,且安全、美观、适应性强,在许多大跨度桥梁中得到广泛应用[2-3],前景广阔。近年来,国内外学者对钢与混凝土组合梁的力学性能做了大量研究[4-5],刘劲等[6]研究了负弯矩作用下组合梁的抗弯刚度,提出了新的组合梁折减刚度法。L.ZHU等[7-8]分别对考虑时变效应、扭转变形和双轴滑移的曲线钢-混凝土组合梁进行了有限元分析。夏叶飞等[9]对弹性状态下曲线组合箱梁的挠度值进行了试验研究,结果表明,挠度值与荷载线性相关,不受工况的影响。LIN Weiwei等[10-11]研究重复加载、钢纤维混凝土(SFRC)和曲率对组合梁结构受力性能的影响。LIN Xinpei等[12]研究了混凝土收缩俆变和温度变化对组合梁力学性能的影响。李运生等[13]对曲线组合箱梁桥的横隔板间距进行了研究,给出了适用于使用阶段的理论计算公式。C.MANTHA等[14]研究了支撑构件刚度和支撑数量对双梁板的横向扭转屈曲和强度的影响。蒋丽忠[15]、李兴[16]等基于能量法分析了钢-混凝土组合梁的侧向稳定性。

上述研究中,对于曲线钢-混凝土组合梁稳定性的研究较少,且计算模型多为没有考虑上翼缘侧向变形的畸变屈曲[15-16]。在负弯矩区,曲线钢梁翼缘可能会因为承受的荷载较大而提前发生侧向失稳,对结构不利。我国现行规范主要采用钢梁的设计方法来计算组合梁结构的稳定性,与组合梁失稳的实际情况有一定差距。因此,对曲线组合梁稳定性的理论研究意义重大。基于此,笔者基于能量法研究负弯矩区工字形曲线组合梁的侧向失稳,建立考虑钢梁上、下翼缘均发生侧向弯曲变形与扭转变形的失稳模型,给出等端弯矩作用下曲线组合梁负弯矩区临界弯矩计算公式。计算分析混凝土板厚度、腹板高厚比(高度一定)、底板宽厚比(厚度一定)、曲率半径、钢筋用量和跨度对临界弯矩的影响。结果表明,腹板高厚比、底板宽厚比和曲率半径对临界弯矩的影响显著。

1 基本假定

工字形曲线组合梁的截面尺寸和坐标系布置分别如图1、图2所示。为便于计算,做如下基本假定[17]:

图1 曲线组合梁截面参数

图2 曲线组合梁的坐标系

①曲线组合梁的截面处处相等；

②曲线组合梁的侧向变形足够小；

③侧向失稳前,不考虑弯曲变形对侧向变形的影响；

④侧向失稳时,不考虑曲线钢梁翼缘形状的变化；

⑤不考虑曲线组合梁的扭转变形、残余应力以及初始缺陷；

⑥负弯矩区只考虑翼缘板中钢筋的抗弯能力。

2 钢梁失稳模型

钢梁下翼缘受外荷载作用时,将引起上、下翼缘均发生扭转变形和侧向弯曲变形。钢梁失稳计算模型如图3所示。

图3 钢梁失稳计算模型

依据钢梁上下翼缘的变形协调关系得出梁腹板的侧向位移为

(1)

式中:uA、uB分别为钢梁上、下翼缘横向位移;φA、φB分别为钢梁上下翼缘扭转角;uw为肋板横向位移;h0为曲线组合梁钢梁上翼缘重心至下翼缘重心的距离。

3 工字形曲线组合梁侧向失稳总势能

基于能量法推导等端弯矩M作用时工字型曲线组合梁钢梁上、下翼缘及混凝土板应变能。

3.1 曲线组合梁应变能

由材料力学[18]知,应变能为

(2)

式中:M为组合梁截面弯矩,规定组合梁上翼缘受拉方向为正方向;E为钢材弹性模量;I为钢梁抗弯惯性矩。

由式(2)计算曲线组合梁钢梁上、下翼缘侧向弯曲及扭转应变能,混凝土板约束应变能分别为

(3)

(4)

(5)

(6)

(7)

腹板弯曲应变能由薄板小挠度理论[19]求解得:

uBφA-uBφB)

}dz.

(8)

3.2 曲线组合梁的外力功

3.2.1 等端弯矩作用时的截面应力

当等端弯矩M作用时,由变形协调条件确定曲线组合梁的双力矩,由力的平衡条件确定曲线组合梁的弯矩,分别表示为

(9)

(10)

工字形曲线组合梁截面的应力[20]为

(11)

由式(11)可得工字形曲线组合梁钢梁上翼缘应力σtf、下翼缘应力σbf及腹板应力σw分别为

(12)

(13)

(14)

其中，

式中:βM为组合梁截面圆心角;ω为主扇形坐标;R为曲率半径;K为广义翘曲扭转系数;η为与K和R有关的系数,η=1/[1+(KR)2];h0为钢梁上翼缘重心至下翼缘重心距离;Ix为组合梁绕x轴惯性矩;Iω为扇形惯性矩;Bω为组合梁截面双力矩;Aa为钢梁上翼缘;Aw为钢梁下翼缘;Ab为钢梁腹板面积;As为组合梁截面纵向钢筋面积;ys为组合梁截面纵筋重心距x轴距离。

3.2.2 曲线组合梁的外力功

外力势能V与外力功W之间的关系表示为V=-W。

(15)

综上所述,工字形曲线组合梁的总势能表示为

Π=U1+U2+U3+U4+U5+U6-W.

(16)

将式(3)～ 式(8)、式(15)代入式(16)即可得曲线组合梁总势能的计算公式。

4 工字形曲线组合梁侧向失稳临界弯矩

基于势能驻值定理推导曲线组合梁侧向失稳临界弯矩。

(17)

由δΠ=0,得一元四次方程,求解可得曲线组合梁负弯矩区侧向失稳的临界弯矩。因一元四次方程求解较为复杂,根据实际情况,可将失稳模型进行适当的简化。当不考虑上翼缘形变即uA和φA均为零时,曲线组合梁的总势能为

(18)

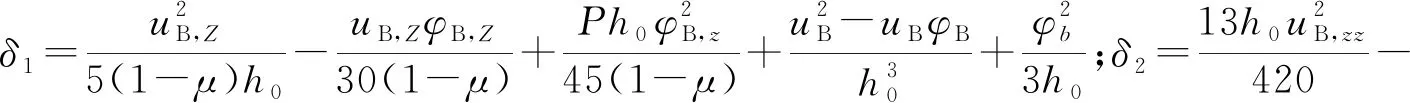
根据势能驻值定理δΠ=0,推得组合梁弯扭失稳时的两个平衡方程为

EIybA1u‴′B=0.

(19)

(20)

假设曲线组合梁侧向弯扭失稳时的侧向位移为n个半波长的正弦函数。

(21)

根据势能驻值定理δΠ=0，得一元二次方程，将式(21)代入此方程计算并简化可得：

(22)

(23)

这两个方程为一组线性齐次方程式,令其系数行列式等于零,求得临界弯矩值为

(24)

(25)

若下翼缘扭转角为0,那么可得到工字型曲线组合梁下翼缘只有横向位移的临界弯矩为

(26)

5 设计参数的影响

计算分析不同曲率半径、不同底板宽厚比、不同腹板高厚比、不同混凝土板厚度、不同钢筋用量和不同跨度下的工字形曲线组合梁负弯矩区侧向失稳临界弯矩。

5.1 曲率半径的影响

图4为曲率半径分别取4 000 mm、5 000 mm、6 000 mm、7 000 mm、8 000 mm时的临界弯矩值。

图4 不同曲率半径下临界弯矩曲线

由图4可知,在同等跨度下,曲线组合梁的临界弯矩与曲率半径呈正相关。曲率半径从4 000 mm增加到8 000 mm,临界弯矩增加了18.5%,且随着曲率半径逐渐增加,临界弯矩增长速度逐渐减小。

5.2 底板宽厚比的影响

定义bbf/tbf为工字形曲线组合梁的底板宽厚比(底板厚度一定)。底板宽厚比为9、11、13、15、17时的临界弯矩曲线如图5所示。

图5 不同宽厚比下临界弯矩曲线

由图5可知,保持底板厚度不变,曲线组合梁的临界弯矩与底板宽厚比呈正相关。底板宽厚比由9增加到17,临界弯矩增加了一倍,且随着底板宽厚比(底板厚度一定)逐渐增加,临界弯矩增长速度逐渐增加。

5.3 腹板高厚比的影响

定义hw/tw为工字形曲线组合梁腹板高厚比(腹板高度一定)。腹板高厚比为25、28、31、34、37时的临界弯矩曲线如图6所示。

图6 不同高厚比下临界弯矩曲线

由图6可知,保持腹板高度不变,曲线组合梁临界弯矩与腹板高厚比呈负相关。腹板高厚比由25变化到37,临界弯矩降低了40%,且随着腹板高厚比(腹板高度一定)逐渐增加,临界弯矩下降速度逐渐减小。

5.4 混凝土板厚度的影响

图7为混凝土板厚度分别为120 mm、130 mm、140 mm、150 mm、160 mm时的临界弯矩值。

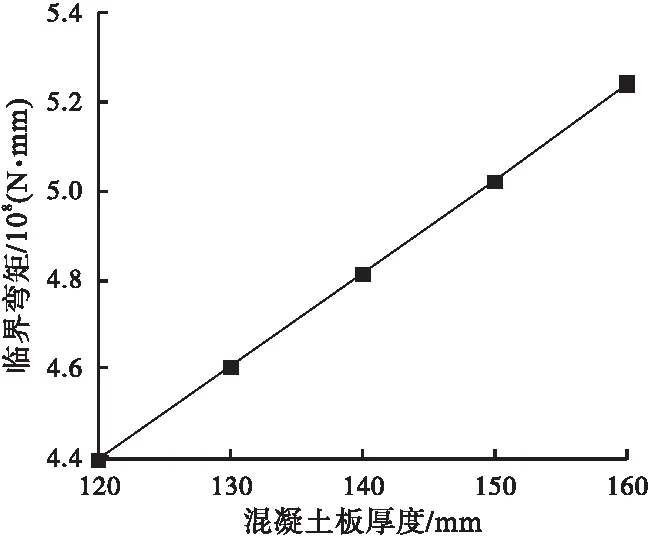
图7 不同混凝土板厚度下临界弯矩曲线

由图7可知,曲线组合梁的临界弯矩与混凝土板厚度呈正相关。混凝土板的厚度由120 mm增加到160 mm,临界弯矩增加了19.1%,且随着混凝土的板厚逐渐增加,临界弯矩也均匀增大。

5.5 钢筋用量的影响

图8为钢筋数量分别为8根、10根、12根、14根、16根时的临界弯矩值。

图8 不同钢筋用量下临界弯矩曲线

由图8可知,曲线组合梁的临界弯矩与钢筋用量呈正相关。钢筋数量由8根增加到16根,临界弯矩增加了8.9%,且随着钢筋用量逐渐增加,临界弯矩增长速度逐渐减小。

5.6 跨度的影响

图9为曲线组合梁的跨度分别为2 000 mm、3 000 mm、4 000 mm、5 000 mm、6 000 mm时的临界弯矩值。

图9 不同跨度下的临界弯矩曲线

由图9可知,曲线组合梁的临界弯矩随着跨度的增加整体趋势逐渐减小。曲线存在回弹,这是因为跨度不一样,失稳半波数不一样,从而导致临界弯矩的回弹。

6 结 论

(1)临界弯矩随着曲率半径、底板宽厚比(厚度一定)、混凝土板厚度和钢筋用量的增加而增大。曲率半径从4 000 mm增加到8 000 mm,临界弯矩增加18.5%。底板宽厚比由9增加到17,临界弯矩增加一倍。混凝土板厚度由120 mm增加到160 mm,临界弯矩增加19.1%。钢筋数量由8根增加到16根,临界弯矩增加8.9%。

(2)临界弯矩随着腹板高厚比(高度一定)和跨度的增加而减小。高厚比由25增加到37,临界弯矩降低40%。随着跨度的增加,曲线组合梁的临界弯矩整体趋势逐渐减小但曲线存在回弹。

(3)临界弯矩受曲率半径、底板宽厚比(厚度一定)和腹板高厚比(高度一定)的影响较大,受混凝土板厚度、钢筋用量和跨度的影响较小。