计及供能可靠性的电-气互联传输网络优化规划
黎静华,王治邦,姜 娟
(广西大学 广西电力系统最优化与节能技术重点实验室,广西 南宁 530004)
0 引言
随着综合能源系统的发展,电-气互联综合能源系统IEGES(Integrated Electricity-Gas Energy Sys⁃tem)将电、气2 种不同能源耦合互补并实现高效利用,有望成为未来能源形式的主流之一[1-2]。未来,只有通过工业基本建设、扩大能源系统规模才能满足用户对于能源不断增长的需求[3]。规划可按能源生产、传输和消纳等环节进行详尽开展,传输网络规划是连接能源生产和消纳的桥梁和纽带,需要兼顾经济性和可靠性。作为能源系统的重要组成部分,优化规划IEGES 传输网络,可保障电-气能源的安全、可靠、经济传输,是实现能源综合利用的重要基础工作[4-5]。
目前,国内外研究学者对IEGES 系统的传输网络优化规划已进行一定程度的研究。文献[6]结合图论,将系统组成划分为2 层,对能量枢纽、输电线路和天然气管道进行规划。文献[7]提出了一种考虑负荷特性互补的能源站网协同规划方法,并针对道路上的管网布局问题,提出相应的优化方法,结合线性优化模型实现了负荷与道路管网接入方向的优化。文献[8]计及天然气系统动态特性,得到热电联产CHP(Combined Heating and Power)机组和电转气P2G(Power to Gas)等耦合元件的最优规划方案。文献[9]考虑需求侧管理,对IEGES 中P2G、燃气机组、输电线路和天然气管道进行协同选址规划。文献[10]在场景分析的前提下建立风电场和P2G厂站的选址优化规划模型。上述关于IEGES传输网络优化规划的研究,在侧重于所研究重点的基础上,都得到了较好的规划方案,但在实现电-气等不同能源转化传输中,有必要考虑对耦合传输网络在规定时间、规定条件下完成能源转化传输能力,从而进一步提升不同或同种能源间的能源利用率。
为此,研究学者进一步在规划中考虑了能源的供给可靠性。可靠性可作为评估规划方案是否具有能源转化传输能力的重要指标,在规划模型中考虑供能可靠性可实现不同能源间高效传输转化。文献[11]基于改造措施与可靠性指标关联规则,实现配电网投资规划方案优选。文献[12]在IEGES中建立了燃气机组、输电线路、天然气供给站和管道的选址定容优化模型,但更偏向于电力系统的供电可靠性研究。文献[13]构建了一种考虑风电不确定性的综合能源系统扩展优化规划模型,但该模型仅考虑电能不足量的可靠性约束,忽略了气网。文献[14]建立了IEGES选址定容优化模型,考虑了切电、热负荷量的可靠性指标约束,但忽略了可靠性对系统规划的影响。上述研究或仅考虑了电力系统的可靠性指标约束,或未侧重于考虑电-气能源双向流动、电力传输、天然气输送这3 个方面的能源传输转化过程中供能可靠性。在工程实际中,用户对于综合能源的持续供给要求越来越高,并且,未来风电等新能源在电力系统的占比将进一步增加。上述得到的规划结果在体现IEGES 高效利用电、气能源的特点方面还可进一步完善,在协调耦合设备(P2G、燃气机组)、电力线路和天然气管道这三者间优化规划关系的同时,使电-气能源双向流动、电力传输、天然气输送可靠高效,达到提升系统经济性和持续供能的效果。
基于此,本文在已有的IEGES研究成果基础上,重点研究了计及供能可靠性的传输网络的规划,包括输电线路、天然气管道、P2G 和燃气机组的选址优化规划。首先,概述IEGES 的详细构成情况,并分析传输网络规划的主要内容。其次,介绍可靠性在IEGES 的重要作用和实际工程意义,针对IEGES 系统具体情况,分别在目标函数和约束条件方面分析可靠性需求和物理含义。然后,在原有的电力系统、天然气系统和耦合元件规划模型的基础上,建立考虑系统供能可靠性的IEGES 中输电线路、天然气管道、燃气机组和P2G 的选址优化规划模型;在求解模型方面,采用增量分段线性化的方法对天然气管道约束进行线性化处理,将原混合整数非线性规划MINLP(Mixed-Integer NonLinear Programming)问题转化为混合整数线性规划MILP(Mixed-Integer Linear Programming)问题,并在MATLAB 平台上实现求解。最后,基于IEEE 39 节点与比利时NGS 20 节点联合系统进行仿真,分析了4 种场景下的最优规划方案、规划成本、风电消纳能力和可靠性效果,验证了模型的可行性和求解方法的有效性。
1 IEGES及其传输网络规划
IEGES 可实现电、气能源之间的能量转换,其结构如图1 所示。IEGES 由电力系统、天然气系统和耦合环节构成,其中耦合环节有燃气机组和P2G,这些耦合元件将电力网络和天然气网络紧密联系在一起,构成了能源可靠双向流动、闭环运行的IEGES;同时电、气能源在各自子系统中通过传输网络实现能源可靠传输。IEGES 中,电、气能源传输至负荷的可靠性尤为重要,关系到IEGES的实用价值。
传输网络规划是IEGES 的基础,直接关系到系统整体功能及其可靠性,其通过确定在何时、何地投建何种类型的网络传输元件来实现规划周期内所需要的供能能力,在满足各项技术指标的前提下使系统的费用最小。由图1 可知,本文传输网络的规划对象包括电力线路、电-气耦合元件(P2G、燃气机组)和天然气输气管道。通常根据电力、天然气负荷预测及电源、气源规划对传输网络的这3 个对象进行规划。
在负荷方面,考虑电力负荷和天然气负荷。在负荷预测数据中,考虑电力、天然气负荷可能发生的不确定场景,计及负荷年平均增长率,采用10 a(每年按365 d 计)的数据作为其可能发生的场景。在能源供给方面,考虑常规电源、风电和气源,电、气源部分分别采用常规传统的发电机组和天然气井,按照给定的规划容量进行计算;风电部分主要考虑其可能发生的不确定场景,采用10 a 的数据作为其可能发生的场景。基于上述的电力负荷、天然气负荷、电源布局和天然气源布局等在规划年限内的基本情况,以此作为边界条件,对如图1 所列的3 个规划对象进行规划。
2 计及供能可靠性的IEGES
可靠性可分为充裕性和安全性,类比于传统、单一的供能系统,IEGES 的可靠性可引申为IEGES 中的各组成元件、运行设备及系统在规定的时间内和一定条件下所完成其规定供能任务的能力,其重要程度体现在IEGES的各个环节中,如图2所示。
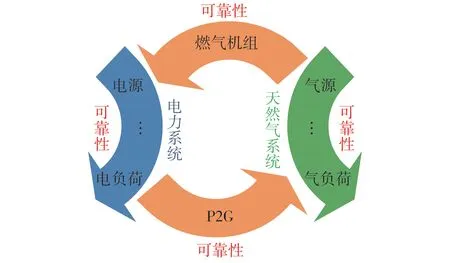
图2 IEGES及其供能可靠性Fig.2 IEGES and its energy supply reliability
IEGES 中,可由允许切电、气负荷量代表IEGES在研究时间内,不能够满足供应负荷需求而导致的切电、气负荷量。当系统中考虑风电时,系统的弃风量代表IEGES 发生弃风现象的严重程度。因而,为了更好地评估IEGES的可靠性和系统的弃风严重程度对IEGES 传输网络规划结果的影响,在IEGES 优化规划模型中采用允许切电负荷量、允许切气负荷量和系统弃风量等来表征系统供能可靠性,并分别在目标函数和约束条件中进行体现。
2.1 目标函数
IEGES 规划通常将IEGES 在规定年限的总建设成本与运行成本之和的净现值最小作为目标函数。随着综合能源系统的不断发展,负荷点对系统供能可靠性的要求越来越高,在对综合能源系统进行优化规划时,其可靠性逐渐被纳入考虑的范围。当前,可以通过将供能不足成本的罚函数[15]等添加到规划的目标函数中来体现对系统供能可靠性的影响,本文在目标函数中添加了计及可靠性约束的能量短缺成本和系统弃风成本的罚函数。
1)计及供能可靠性约束的能量短缺成本。
考虑到负荷高峰时段IEGES可能会出现因无法满足负荷需求而切负荷的现象,用年度切负荷量与能量短缺成本的乘积来表征IEGES可靠性的能量短缺成本。即在规划周期内第τ年的能量短缺成本Cens(τ)为:

2)计及供能可靠性约束的弃风成本。
采用单位弃风成本与年系统弃风总量的乘积来表征IEGES可靠性的弃风成本。即在规划周期内第τ年的弃风成本Cw(τ)为:
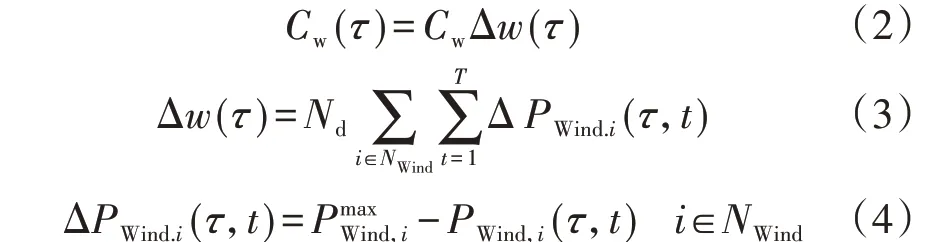
式中:Cw为系统的单位弃风成本;Δw(τ)为第τ年弃风总量;NWind为风电机组的节点集合;为风电机组i有功功率最大值;PWind,i(τ,t)为第τ年时段t风电机组i有功功率;ΔPWind.i(τ,t)为第τ年时段t风电机组i的弃风功率,即风电机组i在规划时段有功功率最大值与实际值之差。
基于所建立的模型,在规划年限内,单位电、气负荷量的能源短缺成本和单位弃风成本为给定值,计算得到允许切电、气负荷量和系统弃风量等变量值,最终计算得到“计及供能可靠性约束的能量短缺成本”值和“计及供能可靠性约束的弃风成本”值。此外,通过年度切电、气负荷量和弃风量等变量值,分别在模型的电力系统节点功率平衡、天然气系统节点流量平衡和变量限制等约束条件方面,建立与目标函数中可靠性因素的联系,从而获得满足可靠性约束的规划结果。
2.2 约束条件
IEGES 规划问题一般需要考虑的基本约束有:①产需平衡约束,即在规划年限内,不同能源系统的输入应该满足不同类型的负荷需求;②运行约束,如输电线路功率传输/天然气管道流量极限约束、节点电压/气压上下限约束、节点电功率/天然气平衡约束等;③耦合环节约束,即耦合环节在能量转换时的能量守恒;④投运逻辑约束,即设备在使用寿命或投建规划周期内,对拟投建设备的投建状态与设备运行状态的逻辑约束。
通常,约束条件通过计及投资建设约束、各系统运行约束和耦合约束,以此来确定规划对象的最佳设备组合、位置、容量和投建时间。IEGES 具有规模大、设备类型繁多、设备运行特性各异、随机性强等特征,增加了可靠性评估的复杂度[16]。同时,可以在规划模型的约束条件中增加系统可靠性约束来研究系统供能可靠性的影响。本文在IEGES规划模型的约束条件中考虑了允许切电负荷量、允许切气负荷量和系统弃风量的可靠性约束的方式来体现IEGES的可靠性对系统规划结果的影响,以此来保证系统在可靠性的前提下追求系统的经济性。体现年度允许切电、气负荷量和系统弃风量等指标的约束分别如下:


3 计及供能可靠性的IEGES传输网络优化规划模型
基于上述理论基础,建立考虑供能可靠性的IEGES 优化规划模型,在对IEGES 中的输电线路、天然气管道、P2G 和燃气机组进行优化规划时,考虑经济技术条件约束和系统供能可靠性的影响。
3.1 目标函数
以规划年限内IEGES的总成本净现值最小为优化目标,总成本包括投资成本、运行成本、计及供能可靠性约束的能量短缺成本和弃风成本四部分。
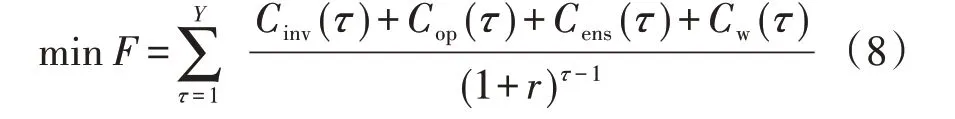
式中:F为规划年限内的总成本;Y为规划年限;r为折现率;Cinv(τ)和Cop(τ)分别为IEGES在规划年限内第τ年的投资成本和运行成本。
1)投资成本。
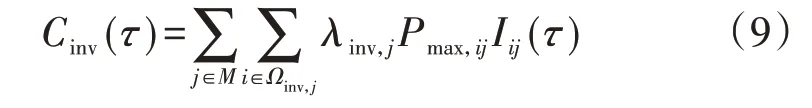
式中:M为候选设备种类集合;Ωinv,j为第j类候选设备集合;λinv,j为第j类候选设备单位容量投资成本;Pmax,ij为节点i处第j类候选设备额定容量;Iij(τ)为0-1变量,表示节点i处第j类候选设备第τ年新增情况(新增时取值为1,非新增时取值为0)。
2)运行成本。
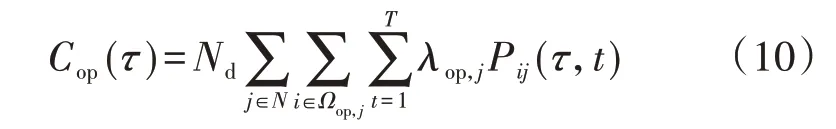
式中:N为运行设备种类集合;Ωop,j为第j类运行设备的集合;λop,j为第j类运行设备的单位容量运行成本;Pij(τ,t)为第τ年时段t节点i处第j类运行设备有功功率。
3)计及供能可靠性约束的能量短缺成本。
计及供能可靠性约束的能量短缺成本Cens(τ)模型见2.1节。
4)计及供能可靠性约束的弃风成本。
计及供能可靠性约束的弃风成本Cw(τ)模型见2.1节。
3.2 约束条件
约束条件考虑电力系统运行约束、投资建设约束、天然气系统运行约束、电气耦合转换约束和供能可靠性约束。
3.2.1 电力系统运行约束
1)常规发电机组约束。


3)输电线路约束。
输电线路的有功与节点电压相角之间的线性关系可用式(14)和式(15)来表示。

式中:PNGFP,i(τ,t)为第τ年时段t节点i处燃气机组输出有功功率;PP2G,i(τ,t)为第τ年时段t节点i处P2G消耗有功功率;PD,i(τ,t)为第τ年时段t节点i处电力负荷。
5)电力系统备用容量约束。
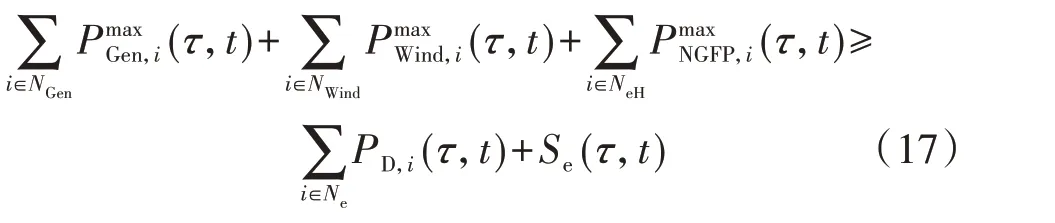
3.2.2 投资建设约束
设定各候选设备在规划年限内只能新建1 次,其表达式为:
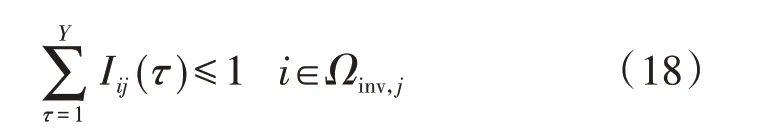
3.2.3 天然气系统运行约束
1)气源点出气约束。

3)天然气管道约束。
本文使用Weymouth 稳态潮流模型[10,17]来描述天然气管道输送流量与两端节点气压之间的非线性关系,如式(23)和式(24)所示,传输流量极限约束可用式(25)来表示。

式中:FP2G,m(τ,t)为第τ年时段t节点m处P2G 设备注入气流量;FNGFP,m(τ,t)为第τ年时段t节点m处燃气机组消耗天然气量;FD,m(τ,t)为第τ年时段t节点m处天然气负荷。
3.2.4 电气耦合转换约束
燃气机组和P2G设备容量限额约束可分别用式(27)和式(28)来表示,能量转换平衡约束可用式(29)来表示。

3.2.5 供能可靠性约束
供能可靠性约束模型见2.2节。
3.3 模型求解
所建立的计及供能可靠性的IEGES传输网络优化规划模型为MINLP 问题,求解处理复杂度高,较为繁琐,速度有待提高。为降低求解难度,采用增量分段线性化法[18-19]对模型中天然气管道约束的非线性部分进行线性化处理,使模型转化为MILP 问题,降低求解难度。
3.3.1 天然气管道非线性模型的线性化
1)模型的非线性部分。
目前所建立的模型中,如式(23)所示,天然气管道模型的节点气压(式(23)等号右边)与管道流量(式(23)等号左边)均为非线性,同理式(24)也为非线性,式(23)和式(24)的非线性无疑给整体模型求解带来了难度。而模型其余部分为线性,因此对天然气管道模型进行线性化处理,可将模型非线性部分转换为线性。
2)线性化过程。
此处以式(23)为例进行说明,该公式含2 个非线性部分,引入新的变量ζ(τ,t)和fmn(τ,t)分别替换节点气压的平方项和管道流量的非线性项:
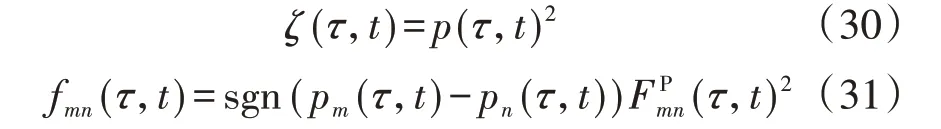
则式(23)可改写为:
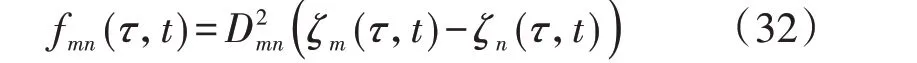
然后,将fmn(τ,t)采用增量分段线性化的方法进行线性化处理,其具体的线性化步骤如下:
(1)根据优化模型的规模和特点,综合考虑求解速度和线性化精度,确定合适的线性化分段子区间数Ns;

式中:Ns为天然气管道输送流量分段子区间数;δmn,k(τ,t)为第τ年时段t天然气管道(m,n)在第k个分段区间上的位置,其取值范围为[0,1];ωmn,k(τ,t)为二进制变量,由二进制约束和式(36)来确定。式(33)表示管道流量FPmn(τ,t)在取值范围的子区间划分;式(34)采用增量分段线性化法描述管道输送流量与节点气压之间的非线性关系;式(35)限制分段线性化时区间变量在Ns上连续取值,不出现跳跃。
3)线性化之后的表达式。
经过上述的线性化过程,可将原建立的MINLP问题规划模型中非线性部分,即式(23),转换为如式(30)—(36)所示的线性化形式。同理,模型中式(24)也可用上述增量分段线性化的方法来进行线性化处理。
3.3.2 优化规划模型的求解
通过上述增量分段线性化法进行线性化处理后,可将原MINLP问题,即式(1)—(29),转化为MILP问题,即式(1)—(22)、式(25)—(29)和式(30)—(36)。转化后的模型,根据电、气负荷计及年平均增长率的特点,选择合适的线性化分段子区间数,以实现MILP问题的求解。在MATLAB平台上使用YALMIP工具,并调用CPLEX优化求解器进行求解。
4 算例分析
4.1 算例说明
本文基于修改的IEEE 39 节点[10]与比利时NGS 20节点系统[17]进行仿真,其系统结构如附录A 图A1所示。IEEE 39 节点电力系统包含46 条原有输电线路、10条候选输电线路、10台常规发电机组和2台风电机组,2台风电机组分别位于节点9、13;NGS 20节点天然气系统包含19 条原有天然气管道、7 条候选天然气管道、2个气源点和4台储气装置。电力系统中的节点31—34 分别通过耦合元件与天然气系统中的节点1、12、14、20 相连,包含4 套燃气机组和4套P2G 设备,本文候选设备为规划年限内待投资建设的线路、管道和耦合元件。
给定规划周期为10 a,年平均折现率为6%,电、气间的等热值转换系数为0.01 MW·h/m3,假定规划周期内电负荷和气负荷的年平均增长率分别为2.5%和1.2%,典型日电、气负荷曲线如附录A 图A2所示。IEEE 39节点与比利时NGS 20节点联合系统的天然气管道参数、电力负荷参数、各元件参数分别如附录A表A1—A3所示。
本文根据规划类型和是否考虑可靠性,设计了以下4种情景来验证模型和方法的有效性,如表1所示。表中,以10 a 的仿真时长中某1 h 为例,列出了4 种情景下的变量数、整数变量数、等式约束及不等式约束等信息。需要说明的是,解耦、耦合规划的区别在于是否对IEGES 耦合元件进行规划;是否考虑供能可靠性的区别在于目标函数和约束条件是否计及可靠性因素,即未考虑可靠性时,目标函数中忽略计及供能可靠性约束的能量短缺成本和计及供能可靠性约束的弃风成本,约束条件中忽略体现年度允许切电、气负荷量和系统弃风量等指标的约束。然后,分析耦合优化规划和考虑系统供能可靠性对IEGES 的规划方案、规划成本、风电消纳能力和可靠性效果等方面的影响。
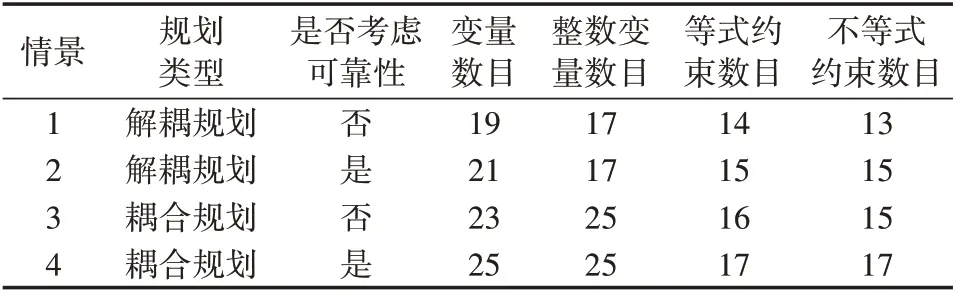
表1 仿真情景Table 1 Simulation scenarios
4.2 规划方案对比分析
为验证IEGES 耦合优化规划模型的有效性,将情景1—4 中的最优规划方案进行比较。表2 给出了上述4种情景所求解得到的最优规划方案。表中,(·)中的数字表示新建的输电线路/天然气管道/候选耦合元件所在的系统节点,[·]中的数字表示新建的年份,例如(1,16)[7]表示第7 年天然气网络在节点1、16 之间新建一条天然气管道,P2G(31)[10]表示第10 年在电力系统的节点31 处新建一套P2G设备。
从表2 可以看出,情景1—4 在规划年限内的最优规划方案都是不相同的。由此可以说明,系统的可靠性、耦合因素对电力系统和天然气系统的最优规划方案有一定的影响。从可靠性方面而言,情景2 相比于情景1,输电线路(10,20)节点规划时间由第8 年变为第1 年;同时,情景4 相比于情景3,输电线路(10,20)节点规划时间也发生变化,情景3第10年在电力系统节点31 新建一套P2G 设备。从耦合因素方面而言,情景3 和4 分别在情景1 和2 的基础上,第1年在电力系统的节点34新建一套燃气机组,第10年在电力系统的节点31、34各新建一套P2G设备,以及在天然气系统中,改变了在节点1、16 之间天然气管道的新建年份。
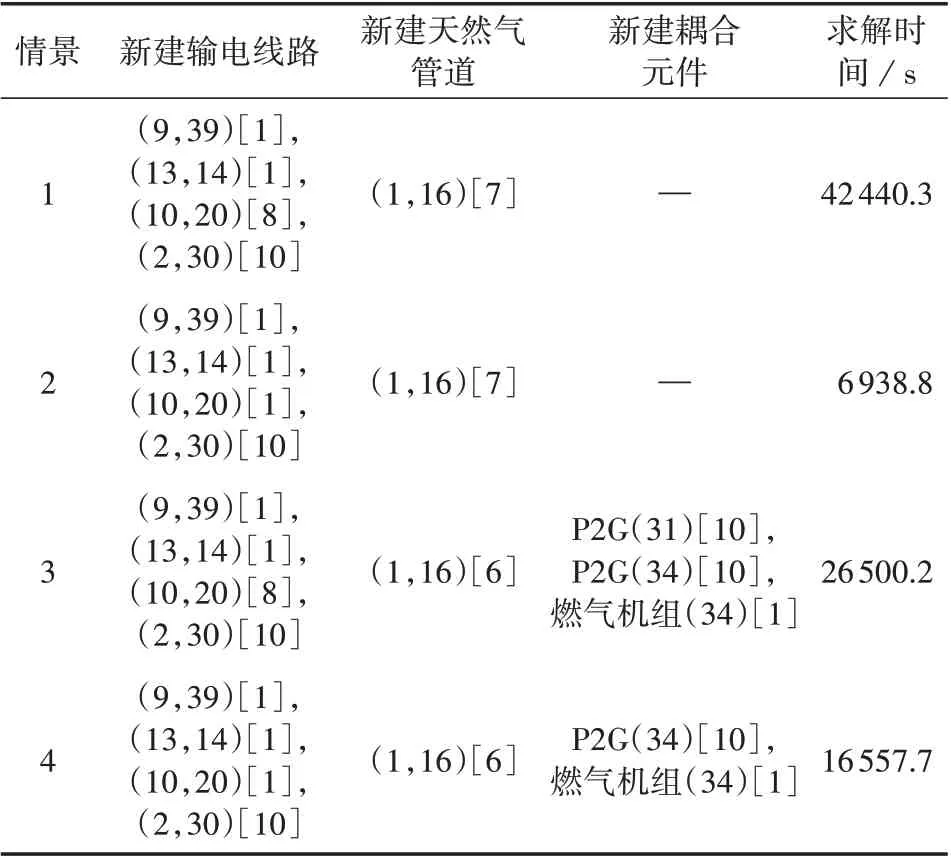
表2 4种情景下的最优规划方案Table 2 Optimal planning scheme under four scenarios
4.3 规划成本对比分析
图3 展示了在规划年限内的各项成本对比分析结果,图中数值的单位为亿元。各项成本包括投资成本、运行成本、计及可靠性约束的能量短缺成本和弃风成本。情景3 较情景1 的运行成本减少了1.47亿元,而投资成本增加了0.50 亿元。由于电力负荷与天然气负荷的峰谷期不完全重合,在情景3 中经过耦合优化规划后,可以实现电、气能源相互转化,减小IEGES 的运行成本。结合表2 所示的最优规划方案,由于新建燃气机组和P2G 设备,增加了投资成本;但由于运行成本的减少要大于投资成本的增加,即情景3 的总成本低于情景1。由此可以说明,与单一的电力网络和天然气网络的独立规划相比,电力网络和天然气网络的耦合优化规划有助于提高IEGES 在规划运行时的经济性。情景2 与情景4 的比较同理。
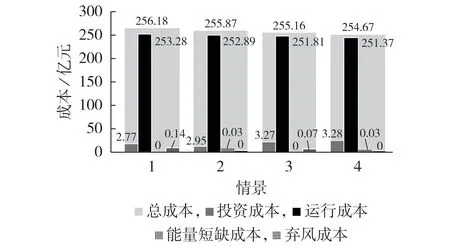
图3 4种情景下的成本对比分析Fig.3 Comparative analysis of costs among four scenarios
另外,与未考虑供能可靠性的情景1 相比,情景2 减少了0.39 亿元的运行成本且弃风成本接近为0,增加了0.03亿元的能量短缺成本和0.18亿元的投资成本,且总成本低于情景1。由此可知,考虑了可靠性的情景2比未考虑可靠性的情景1的经济性要好。在考虑了系统可靠性之后,风电的利用率得以提高,降低了系统的运行成本。情景4综合了情景3耦合优化规划和情景2 考虑系统可靠性的优点,总成本最低。由此可以说明,电力系统与天然气系统的耦合优化规划和考虑系统供能可靠性均可以提高IEGES在规划、运行时的经济性。
规划方案下各组成部分成本具体情况如附录A表A4所示。投资成本部分含线路和天然气管道,运行成本部分含电源和气源。在投资成本部分,4 种情景中的电网投资线路的成本都高于气网投资管道的成本。电网中,可靠性对线路投资成本(对比情景1、2 或情景3、4)的影响较大,而耦合规划对线路投资成本(对比情景1、3或情景2、4)的影响较小;气网中,耦合规划对管道投资成本(对比情景1、3 或情景2、4)的影响较大,可靠性对管道投资成本(对比情景1、2 或情景3、4)的影响较小。在运行成本部分(主要分析电源和气源),无论是气网或电网,情景1的运行成本是最高的,情景4 的运行成本是最低的,可见进行耦合规划和考虑可靠性之后降低了系统的运行成本。可靠性指标部分,体现年度弃风量指标在考虑可靠性后接近为0(情景2、4),耦合规划后相比于规划之前有所降低(对比情景1、3)。体现年切电负荷量指标为0,年切气负荷量指标为11 199.1 m3。耦合设备部分,耦合规划之前(情景1、2),耦合设备投资成本为0;耦合规划之后(情景3、4),考虑可靠性的情景4相比于未考虑可靠性的情景3,投资成本有所减少,并且情景4的总成本也为最小。
4.4 风电消纳能力对比分析
为了研究电力系统与天然气系统耦合优化规划和系统供能可靠性对系统风电消纳能力的影响,图4展示了规划年限内情景1—4下风电机组1某一典型日各时段(将一天等分为24个时段)的弃风曲线。
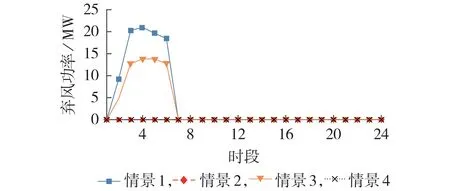
图4 典型日弃风曲线Fig.4 Daily curves of wind curtailment
通过对比情景1 和情景3 可以看出,在时段00:00—07:00,弃风功率减少了34.63%,原因是情景3 下P2G 设备在电力负荷的低谷时段,可将富余风电转化为天然气进行运输、存储和使用,消纳风电,减少弃风现象的发生。由此可知,相较于传统的电力系统和天然气系统的独立规划,通过对IEGES进行耦合优化规划,可以促进风电的消纳,从而减缓系统弃风现象的发生。
将情景2 与情景1 的弃风功率进行比较可以发现,情景2 下弃风功率减少至接近为0;由于情景2下目标函数中考虑了系统的弃风功率最小,促使风电的利用率得以提高,从而提高了风电消纳的能力,减少了系统的弃风。综上所述,无论是采用耦合优化规划的情景3,还是考虑可靠性的情景2,皆可以提高风电的利用效率。
4.5 供能可靠性对比分析
为了研究系统供能可靠性对IEGES耦合优化规划效果的影响,即在情景3 下目标函数中未计及供能可靠性约束的能量短缺成本和弃风成本,约束条件中未计及体现年度允许切电、气负荷量和系统弃风量等指标的约束。图5 给出了情景3 和4 在规划年限内的各项成本的对比结果。
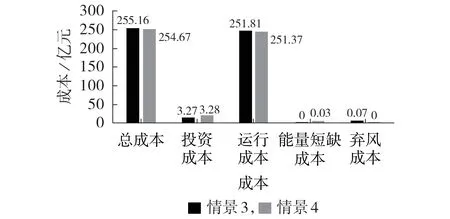
图5 情景3和情景4成本对比分析Fig.5 Comparative analysis of costs between Scenario 3 and Scenario 4
由图5 可知,情景4 相较于情景3 的运行成本降低了0.44亿元,能量短缺成本增加了0.03亿元,弃风成本为0,总成本降低了0.49 亿元。在考虑了系统的供能可靠性之后,促使IEGES 增强了电力系统和天然气系统间能量的双向流动,提高了能源的利用效率,从而降低了系统的运行成本。虽然情景4 因为考虑可靠性的影响增加了0.03亿元的能量短缺成本和0.01 亿元的投资成本,但相较于运行成本的减少,情景4的总成本还是要低于情景3。由此可以说明,在IEGES中考虑系统供能可靠性的影响,可以提高IEGES在规划运行时的经济性。
另外,为了研究IEGES 的耦合优化规划在系统供能可靠性效果方面的影响,图6展示了情景2与情景4在规划年限内的各项成本对比分析图。
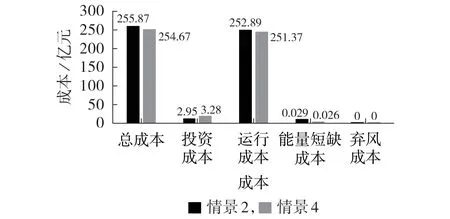
图6 情景2与情景4成本对比分析Fig.6 Comparative analysis of costs between Scenario 2 and Scenario 4
由图6 可知,除了情景4 的投资成本比情景2 增加了0.33 亿元之外,情景4 的运行成本和总成本分别比情景2 降低了1.52 亿元和1.20 亿元。由此可以说明,电力系统和天然气系统通过燃气机组和P2G设备的耦合优化规划提高了系统在规划运行时的经济性。情景4的能量短缺成本较情景2减少了0.003亿元,即情景4 较情景2 的可靠性得到进一步提升。综上所述,对IEGES 进行耦合优化规划,不仅能够提高IEGES 在规划运行时的经济性,还可以提高IEGES在规划运行时的可靠性。
5 结论
针对IEGES 中耦合元件、输电线路和天然气管道的选址优化规划问题,构建了计及供给可靠性的IEGES 选址优化规划的模型。对于模型呈非线性的特点,采用增量分段线性化法对模型中的非线性部分进行线性化处理,将原MINLP 问题转化为MILP问题进行求解。仿真案例表明考虑供给可靠性的IEGES 耦合传输优化规划可以提高系统在规划和运行时的经济性、可靠性和风电消纳能力。
随着综合能源系统的不断发展,IEGES 的优化规划和可靠性评估将不断得到完善,在考虑可靠性对IEGES 优化规划的影响时,如何使IEGES 的可靠性评价指标体系更加完善是后续研究亟待解决的问题。
附录见本刊网络版(http://www.epae.cn)。

