考虑综合需求响应的气电联合系统可靠性评估
龚凌霄,刘天琪,何 川,南 璐,苏学能,胡晓通
(1. 四川大学 电气工程学院,四川 成都 610065;2. 国网四川省电力公司电力科学研究院,四川 成都 610094;3. 国网四川省电力公司调度控制中心,四川 成都 610094)
0 引言
能源互联网是以电力为枢纽和平台的新一代能源系统,是支撑能源革命的变革性技术之一[1]。由电力系统和天然气系统耦合而成的气电联合系统作为能源互联网的重要组成部分,对促进可再生能源消纳、实现低碳环保具有重要意义。近年来,随着电力系统和天然气系统耦合程度的加深,传统局限于电、气子系统的可靠性评估已不能实现系统供电、供气可靠性水平的准确量化。因此,有必要建立气电联合系统可靠性模型并研究其可靠性评估方法,以期为综合能源系统的安全运行奠定科学、有效的理论基础。
目前,针对综合能源系统可靠性评估的基本步骤主要包括系统状态获取、系统建模与求解、可靠性指标计算[2]。其中,系统状态获取大多采用蒙特卡洛模拟法。文献[3]将多能流计算与序贯蒙特卡洛法相结合,提出一种综合能源系统序贯模拟可靠性评估方法;文献[4]提出一种马尔科夫链蒙特卡洛方法,将随机过程中的马尔科夫过程引入蒙特卡洛模拟中,实现动态蒙特卡洛模拟;文献[5]建立了负荷及风速的不确定性模型,并采用非序贯蒙特卡洛法对系统元件进行抽样;文献[6]采用解析法对气电耦合综合能源系统进行可靠性评估,同时考虑气网故障对供电可靠性的影响。在系统建模与求解方面,文献[7]提出了一种考虑热惯性的综合能源系统优化运行模型;文献[8]建立了区域综合能源系统负荷削减优化模型,并使用粒子群-内点混合优化算法进行求解;文献[9]计及天然气网络状态,对区域综合能源系统中的天然气环节进行稳态建模与潮流计算。上述文献所建立的气电联合系统模型大多是非线性的,求解较为困难。目前对于气电联合系统模型中的非线性天然气潮流方程的处理方法主要有2种:①利用线性化方法将原问题转化为混合整数线性规划模型进行求解;②利用锥优化方法将原问题转化为混合整数二阶锥SOC(Second-Order Cone)规划模型进行求解。文献[10]采用分段线性化方法对著名的Weymouth 稳态天然气潮流方程进行线性化处理;文献[11]采用二阶锥规划方法对电力系统和天然气系统潮流方程进行处理;文献[12]对气网潮流方程进行二阶锥松弛,转化为混合整数二阶锥规划模型进行求解。在可靠性评估指标方面,文献[13]研究并提出了区域综合能源系统的运行可靠性指标;文献[14]考虑弃风现象和电转气(P2G)设备,提出了系统级和设备级的可靠性指标。
需求响应DR(Demand Response)是需求侧负荷参与电网灵活互动的重要途径,国内外的研究表明,需求响应能够在一定程度上维持电力系统稳定性,促进可再生能源消纳,减小负荷峰谷差,降低系统运行成本。近年来,随着能源互联网的发展和不同能源间耦合程度的加深,衍生出多种能源的综合需求响应IDR(Integrated Demand Response)。综合需求响应对维持多能源系统安全运行具有重要意义。2021 年2 月15 日,美国得克萨斯州电网发生大停电事件,这次大停电部分原因在于极寒气候下发电机组和燃气机组出力下降,无法可靠供电,若电负荷与气负荷能提供需求响应,则能够避免一些强制停电的情况。进一步而言,有必要考虑气电联合系统的可靠性,单纯以经济性最优为目标函数的规划问题不能满足极端气候下多能源系统的可靠运行。目前,对于综合需求响应的研究大多侧重于综合能源系统的规划和优化运行[15-18]。文献[15]对综合需求响应的建模方法进行了介绍,提出了一种综合需求响应协调优化模型;文献[16]建立了电热耦合系统的综合需求响应模型,分析了不同响应方案下的可靠性和经济性;文献[17]考虑气电联合需求响应,建立了气电综合能源系统的协调优化调度模型;文献[18]研究了计及电、气、热储能的电、热负荷需求响应,建立了多能源系统负荷削减优化模型并采用蒙特卡洛模拟法对其进行可靠性评估。
通过阅读此类文献,发现在气电联合系统可靠性评估中,还存在以下不足之处:①在气电联合系统可靠性评估模型的求解方面,针对非线性的天然气潮流约束,一般采用分段线性化方法进行求解,但通常难以兼顾求解精度与效率;②在可靠性评估指标方面,较少有文献提出针对气电联合系统的可靠性评估指标;③目前对于气电联合系统可靠性评估问题,鲜有研究考虑电、气负荷综合需求响应对气电联合系统可靠性的影响。
为此,本文首先以电、气负荷削减量最小为优化目标建立气电联合系统负荷削减优化模型,在此基础上利用泰勒级数展开法对约束条件中的天然气潮流约束方程进行线性化处理,同时考虑气网潮流方向和天然气管道运行状态以保证线性化的精确性;其次对典型日内可中断和可转移电、气需求响应负荷进行详细建模,引入电、气负荷综合需求响应以提高系统可靠性;再次为对气网可靠性进行量化分析,将传统电力系统可靠性评估指标扩展到天然气系统,建立切气负荷概率、气量不足时间期望、气量不足期望值作为气网可靠性指标,并提出综合需求响应贡献系数指标来刻画综合需求响应对系统可靠性的影响;此外,由于需求响应对于负荷的调整具有时序性,本文基于序贯蒙特卡洛模拟法获取系统设备元件的运行状态,评估考虑电、气负荷综合需求响应的气电联合系统可靠性;最后对建立的气电联合系统负荷削减优化模型进行仿真分析,验证了本文所提方法的有效性。
1 考虑综合需求响应的气电联合系统负荷削减优化模型
综合需求响应可以显著提高综合能源系统的灵活性和可靠性。为了使系统尽可能避免出现负荷削减现象,或在不可避免时使负荷削减量最小,本文基于典型日建立考虑电、气负荷综合需求响应的气电联合系统负荷削减优化模型以实现该目标。
1.1 目标函数
本节以电负荷和气负荷削减量之和最小为优化目标,建立式(1)所示的目标函数。

式中:ΔPet和ΔGmt分别为时刻t下电负荷节点e和气负荷节点m的负荷削减量。
1.2 约束条件
1.2.1 电力系统运行约束条件
电力系统的运行约束条件包括节点功率平衡约束、传输线路约束、机组运行约束。考虑综合需求响应和电负荷削减,电力系统的节点功率平衡约束方程如式(2)所示。传输线路约束如附录A 式(A1)—(A3)所示。机组运行约束如附录A 式(A4)、(A5)所示。
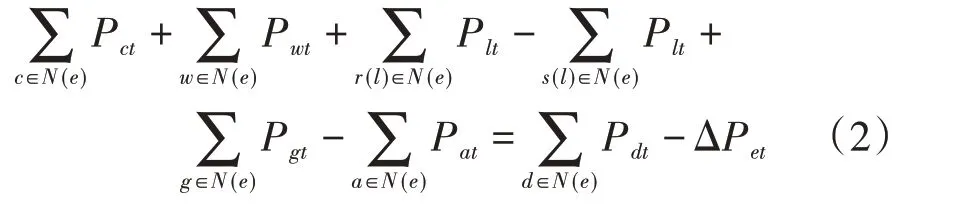
式中:N(e)为电力系统中连接到电负荷节点e的一系列设备集合;Pct为时刻t下非燃气常规机组c的出力;Pwt为时刻t下风电场w的出力;Plt为时刻t下输电线路l的潮流;s(l)和r(l)分别为输电线路l的送端母线和受端母线;Pgt和Pat分别为时刻t下燃气机组g产生的电功率和P2G设备a消耗的电功率;Pdt为时刻t下考虑需求响应后需求侧可响应负荷节点d的电负荷出力。
1.2.2 天然气系统运行约束条件
天然气系统主要由天然气气井、天然气传输管道、天然气负荷组成。与电力系统类似,天然气系统的运行约束条件包括节点能量平衡约束、天然气潮流约束以及设备运行约束等。考虑综合需求响应和气负荷削减,天然气系统的节点能量平衡约束方程如式(3)所示。天然气潮流约束方程如附录A 式(A6)—(A11)所示。设备运行约束方程如附录A 式(A12)—(A17)所示。
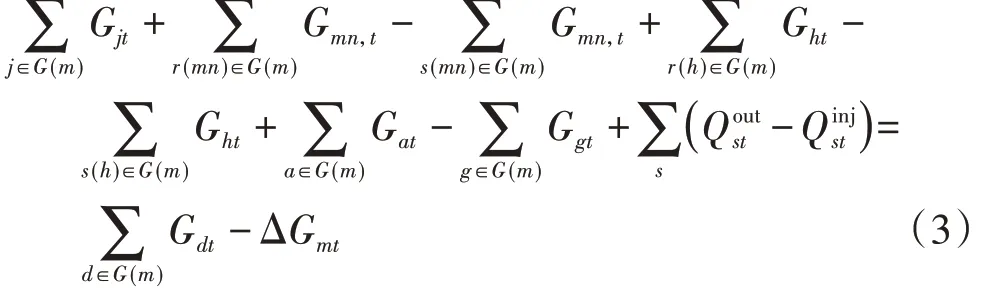
式中:G(m)为天然气系统中连接到气负荷节点m的一系列设备集合;Gjt为时刻t下天然气气井j的产气量;Gmn,t和Ght分别为时刻t下天然气管道mn和压缩机站h所在管道中的天然气潮流;s(mn)、r(mn)和s(h)、r(h)分别为天然气管道mn和压缩机站h所在管道的送端节点、受端节点;Gat和Ggt分别为时刻t下P2G 设备a的天然气产生量和燃气机组g的天然气消耗量和分别为时刻t下储气设备s的注入气量和流出气量;Gdt为时刻t下考虑需求响应后需求侧可响应负荷节点d的天然气消耗量。
1.2.3 耦合设备运行约束条件
电力系统和天然气系统通过P2G设备和燃气机组实现耦合,因此在气电联合系统运行时会受到耦合设备的运行约束。耦合设备的运行约束方程如附录A式(A18)—(A20)所示。
1.2.4 负荷削减量约束条件
电、气负荷削减量受其上下限约束,应保证在系统安全运行的条件下尽可能减小电、气负荷的削减量。电、气负荷削减量约束方程分别如式(4)、(5)所示。
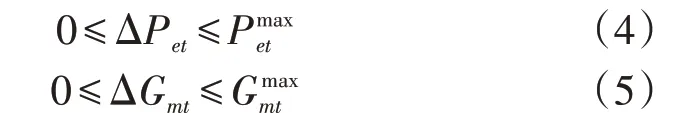
1.2.5 需求响应约束
需求侧可响应负荷分为可中断负荷和可转移电、气需求响应负荷[19]。通过电、气负荷综合需求响应,在系统可靠性受威胁时灵活中断一定量负荷或转移负荷的用电时间,能够更好地匹配可再生能源出力,提升系统可靠性,从而保障系统安全稳定运行。
需求侧可响应电负荷分为可中断电负荷和可转移电负荷,如式(6)所示;需求侧可响应电负荷与电负荷预测值关系如式(7)所示;各时刻下需求侧可中断电负荷和可转移电负荷受一定比例限制,如式(8)、(9)所示;需求侧可中断电负荷与可转移电负荷总量分别满足式(10)、(11);需求响应后的电负荷应满足系统最大电负荷约束,如式(12)所示。

与需求侧可响应电负荷类似,需求侧可响应气负荷满足约束方程式(13)—(19)。

1.3 泰勒级数展开法


由此可得,考虑天然气潮流方向的Weymouth潮流方程可线性化为式(29)、(30)。进一步考虑天然气管道故障,则可表示为式(31)、(32)。
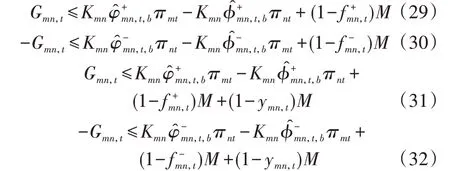
式中:M为足够大的数。综上所述,式(31)、(32)代表了考虑天然气潮流方向和天然气管道运行状态的Weymouth 潮流约束的有效线性近似,因此,可用式(31)、(32)替换附录A 式(A6),将非线性模型转化为混合整数线性规划模型以便于求解。
2 考虑综合需求响应的气电联合系统可靠性评估
2.1 可靠性评估指标
传统电力系统可靠性评估指标主要包括系统切负荷概率LOLP(Loss Of Load Probability)、系统电力不足时间期望LOLE(Loss Of Load Expectation)、系统电力不足期望值EENS(Expected Electric Not Supply)。为实现考虑综合需求响应的气电联合系统可靠性的量化分析,本文将传统电力系统可靠性评估指标扩展到天然气系统,提出切气负荷概率、气量不足时间期望、气量不足期望值指标以评估天然气系统可靠性。各指标具体计算公式[20]见附录A 式(A21)—(A26)。此外,建立需求响应对电力不足期望值贡献系数CDREE(Contribution of De⁃mand Response to Expected Electric not supply)、需求响应对气量不足期望值贡献系数CDREG(Con⁃tribution of Demand Response to Expected Gas not supply)指标,用于刻画需求响应对气电联合系统可靠性的影响,如式(33)、(34)所示。
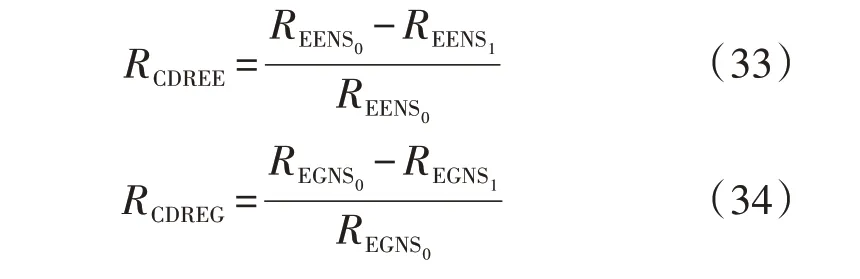
式中:RCDREE和RCDREG分别为需求响应对电力以及气量不足的期望值贡献系数;REENS0和REENS1分别为考虑需求响应前、后的系统电力不足期望值;REGNS0和REGNS1分别为考虑需求响应前、后的系统气量不足期望值。
2.2 可靠性评估方法
基于本文所建立的负荷削减优化模型和可靠性评估指标,利用序贯蒙特卡洛模拟法评估考虑综合需求响应的气电联合系统可靠性。具体评估步骤如下:
1)输入气电联合系统及其元件参数数据,初始化系统元件状态参数;
2)使用序贯蒙特卡洛模拟法在大量抽样年内对系统元件(机组、输电线路、气井、天然气管道等)进行状态抽样,得到系统元件状态和状态持续时间;
3)初始化模拟年数(z=1);
4)选取一个典型日,根据模拟的系统每小时元件状态,利用所建负荷削减优化模型求解该典型日每小时的负荷削减状态和最优负荷削减量;
5)根据优化模型求解结果和所提可靠性评估指标,计算该年系统可靠性指标,并令z=z+1;
6)若模拟年数达到设定的蒙特卡洛模拟时长或可靠性指标方差系数小于设定门槛值,则进入步骤7),否则转至步骤4);
7)统计计算气电联合系统的可靠性指标。
3 算例分析
3.1 算例概况
为验证本文所提可靠性评估方法的有效性,本节以IEEE 24-NGS 12 气电联合系统为例,进行仿真分析。该气电联合系统由修改的IEEE 24 节点电力系统和12 节点天然气系统耦合而成。其中,修改的IEEE 24 节点电力系统包含19 台非燃气机组、7台燃气机组、38 条输电线路以及17 个电力负荷,电峰荷电力系统最大负荷为2850 MW;燃气机组1—4连接电力系统节点1,由天然气系统节点11供气,燃气机组5连接电力系统节点21,由天然气系统节点5供气,燃气机组6、7连接电力系统节点23,由天然气系统节点12 供气;在节点1、2 接入容量为200 MW的风电场,同时配置容量为100 MW 的P2G 设备,在节点22 接入容量为300 MW 的风电场,同时配置容量为150 MW 的P2G设备;P2G设备产生的天然气由节点5、8、11注入天然气系统。
12节点天然气系统包含3个天然气气井、8条天然气管道、2座压缩机站、1台储气设备以及8个天然气负荷,气峰荷天然气系统最大负荷为254 700 m3;储气设备位于天然气系统节点12,该节点的最大注入气量和流出气量之差为14150 m3/h,最大储气容量为113 200 m3。此外,本文元件停运模型采用两状态模型[3],更加详细的气电联合系统参数参考文献[21]。
3.2 泰勒级数展开法的精度分析
通过泰勒级数展开法将Weymouth 天然气潮流方程线性化,可能会存在误差。为了验证本文所提出的泰勒级数展开法线性化近似的有效性,定义最大相对误差指标来评估泰勒级数展开法的外部近似精度,如式(35)所示。
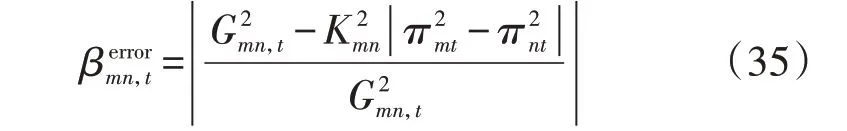
由式(35)可以看出,若给定的气压断点与实际求得的节点气压足够接近,则能保证泰勒级数展开法的最大相对误差足够小。因此,通过设置不同的气压断点数,得到泰勒级数展开法的精度与求解时间如表1 所示。分析表1 可以得出,一方面,增加气压断点数能够有效减小泰勒级数展开法的最大相对误差,从而提高其外部近似精度;另一方面,增加气压断点数也会牺牲部分求解速度。根据表1,气压断点数为500 时较气压断点数为200 时求解速度有所下降,而气压断点数为200 时的最大相对误差已经足够小,因此,在保证求解精度的前提下,为提高求解效率,设置气压断点数为200。
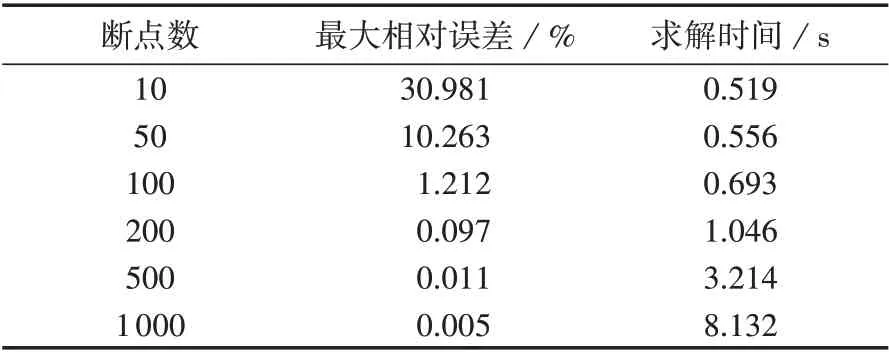
表1 不同气压断点数下泰勒级数展开法的精度与求解时间Table 1 Accuracy and solving time of Taylor series expansion method under different numbers of pressure breakpoints
表2 给出了利用分段线性化法处理天然气潮流方程的精度与求解时间。与表1 对比可以得出,在相同的误差数量级下,分段线性化法的求解效率低于泰勒级数展开法。其中分段数为12 时和气压断点数为200 时的最大相对误差较为接近,但是分段线性化法求解时间明显较长,当最大相对误差低于0.1%时,泰勒级数展开法在求解速度上具有明显的优势。
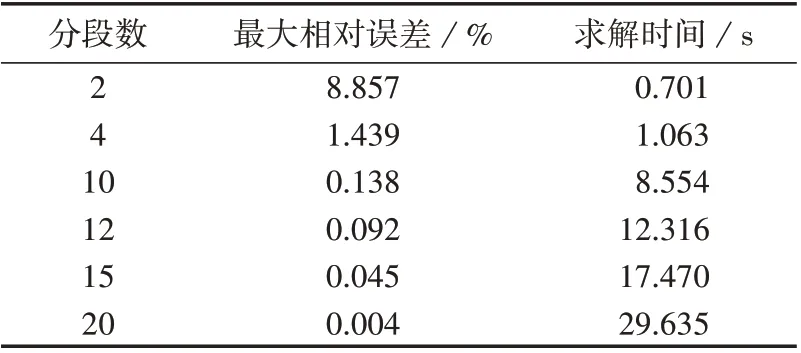
表2 分段线性化法的精度与求解时间Table 2 Accuracy and solving time of piecewise linearization method
在气压断点数为200 的基础上,增大负荷倍数来测试泰勒级数展开法的精度,表3 给出了不同负荷增大倍数下泰勒级数展开法的精度对比。由表3可知,当负荷增大倍数较低时,泰勒级数展开法的精度比较稳定;当负荷增大倍数较高(系统重载情况下)时,由于天然气系统输送能力降低,某些节点的气压达到其上限或下限,泰勒级数展开法的精度有所下降,此时需要设置更多的气压断点数来提高泰勒级数展开法的外部近似精度。
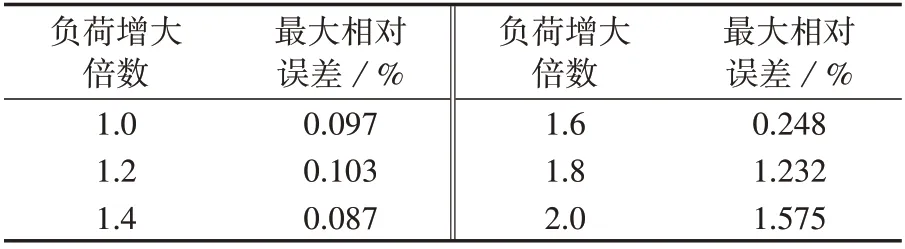
表3 不同负荷增大倍数下泰勒级数展开法的精度Table 3 Accuracy of Taylor series expansion method under different load magnification factors
为探究气压断点数对负荷削减优化模型求解结果的影响,本文计算不同气压断点数下的天然气管道潮流以及某典型日气负荷削减量。图1 给出了某典型日某时刻不同气压断点数下的天然气管道潮流。由图可知,气压断点数为200 时各管道的潮流和气压断点数为500 时各管道的潮流较为接近,气压断点数为500 时各管道的潮流和气压断点数为1 000 时各管道的潮流基本一致,随着气压断点数的增加,模型求得的天然气管道潮流的精确性有所提高。图2 给出了不同气压断点数下某典型日的气负荷削减量。由图可知,当气压断点数较少时,泰勒级数展开法的精度较低;当气压断点数达到一定数量后,系统切气负荷量趋于稳定,求解结果精确性较高。因此,适当增加气压断点数可保证泰勒级数展开法的精度,进而能够保证模型求解结果的精确性。
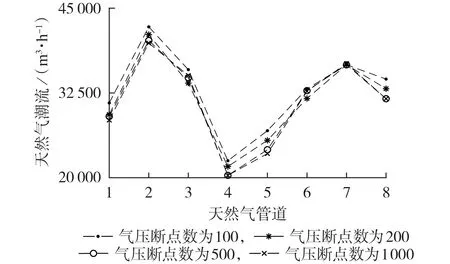
图1 不同气压断点数下的天然气管道潮流Fig.1 Natural-gas flow of pipeline with different numbers of pressure breakpoints

图2 不同气压断点数下某典型日气负荷削减量Fig.2 Typical daily natural-gas load shedding amount with different numbers of pressure breakpoints
此外,为进一步分析泰勒级数展开法的精度对系统可靠性指标的影响,在不考虑需求响应的前提下,设置不同的气压断点数,得到系统切电、气负荷概率指标(RLOELP、RLOGLP)的变化趋势如图3 所示。由图可知,系统切负荷概率指标对泰勒级数展开法精度的敏感性存在转折点。在气压断点数低于100时,由于泰勒级数展开法的精度很低,系统切负荷概率指标的精确性较差,当气压断点数达到100,进一步增加断点数,系统切负荷的概率对泰勒级数展开法的精度将不会太敏感,此时,可以认为系统的切负荷概率是精确的。因此,利用系统切负荷概率指标对泰勒级数展开法精度的不敏感性可以实现较少断点数下系统切负荷概率的精确求解,从而有效提高求解效率。
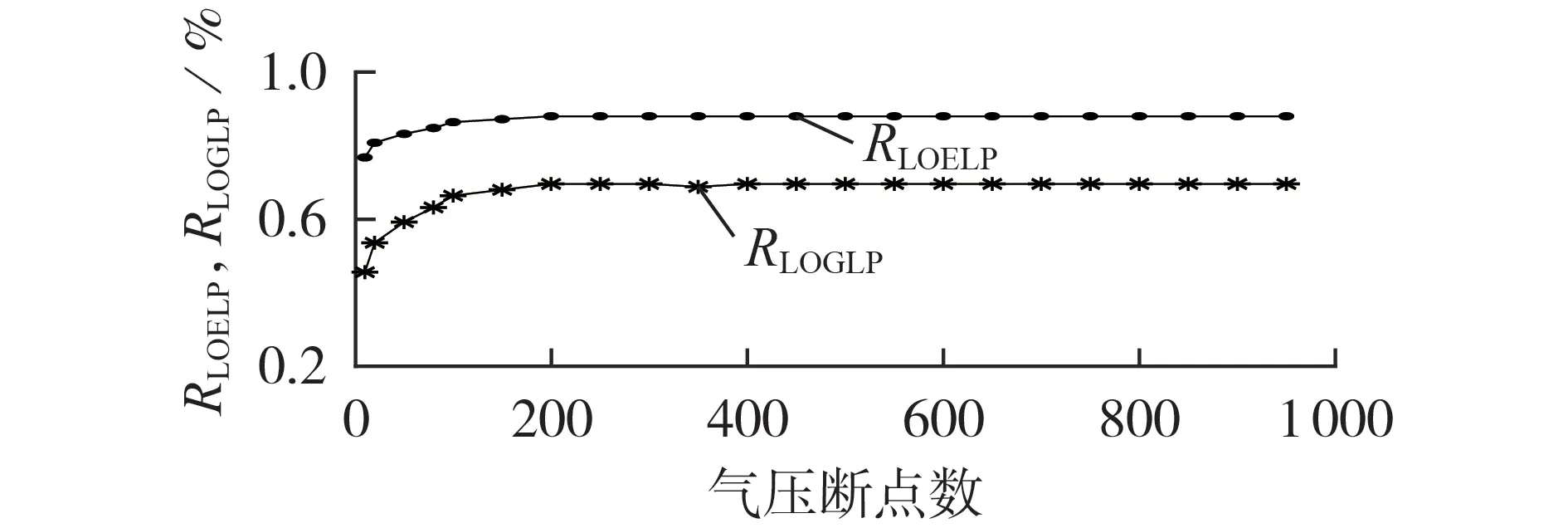
图3 系统切负荷概率指标随气压断点数变化趋势Fig.3 Tendency of probability indexes of system load shedding with different numbers of pressure breakpoints
3.3 气电联合系统可靠性分析
为探究需求响应对气电联合系统可靠性的影响,本节设置以下7 种不同场景:场景①,基础场景,不考虑储气设备、P2G设备以及电、气负荷需求响应;场景②,在场景①的基础上考虑储气设备;场景③,在场景①的基础上考虑P2G设备;场景④,在场景①的基础上同时考虑储气设备和P2G 设备;场景⑤,在场景④的基础上考虑电负荷需求响应;场景⑥,在场景④的基础上考虑气负荷需求响应;场景⑦,在场景④的基础上考虑电、气负荷综合需求响应。
各场景下的需求响应比例见附录B 表B1。仿真计算不同场景下气电联合系统的切电、气负荷概率指标(RLOELP、RLOGLP),系统电力、气量不足时间期望指标(RLOELE、RLOGLE),电力、气量不足期望值指标(REENS、REGNS)以及需求响应对电力、气量不足期望值贡献系数指标(RCDREE、RCDREG),结果如表4 所示。由表可知,以场景①为参考,场景②考虑了储气设备,在气负荷高峰时段供应气负荷需求,提升了天然气系统可靠性。同时,储气设备还可以通过燃气机组间接供应电负荷,因此电力系统可靠性也有所提高。场景③在场景①的基础上考虑了P2G 设备,通过将富余风电转化为天然气,一定程度上缓解了气负荷需求,因此系统气负荷削减概率和气负荷削减量均有所减小。可见,P2G 设备对系统气负荷具有一定的支撑作用。场景④同时考虑了储气设备和P2G设备,相比于场景②、③,气电联合系统的可靠性得到显著改善。
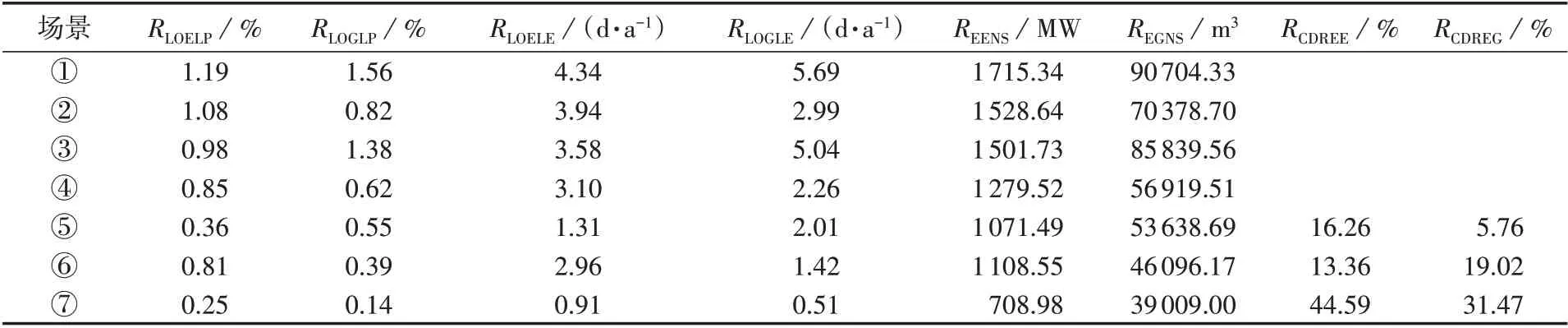
表4 不同场景下的可靠性评估指标计算结果Table 4 Calculative results of reliability evaluation indexes under different scenarios
场景⑤在场景④的基础上考虑了电负荷需求响应,通过在负荷高峰时段中断或转移电负荷,改善了电力系统可靠性。此外,由于电负荷需求响应也在一定程度上减少了电力系统对天然气的需求,因此,系统切气负荷概率指标RLOGLP和系统气量不足时间期望指标RLOGLE均有所减小。场景⑥在场景④的基础上考虑了气负荷需求响应,因此系统中RLOGLP、RLOGLE、REGNS较场景⑤下降更明显,需求响应对气量不足期望值贡献系数指标RCDREG从5.76%增加到19.02%,系统切气负荷量明显减小,天然气系统可靠性显著提升。同时,由于气负荷需求响应降低了天然气系统对天然气的需求,从而间接使得燃气机组能够利用更多的气流发电以供应电负荷,因此,场景⑥系统的切电负荷概率和切电负荷量均有所减小,但下降幅度不及场景⑤,需求响应对电力不足期望值贡献系数也低于场景⑤。与场景⑤、⑥相比,场景⑦考虑了电、气负荷综合需求响应,由表4 可知,系统切电、气负荷概率和切电、气负荷量相比于单一考虑电、气负荷需求响应更低,综合需求响应对于气电联合系统电力、气量不足期望值的贡献高于单一需求响应贡献的简单叠加。因此,考虑电、气负荷综合需求响应能够有效减小气电联合系统的失负荷量。综上所述,考虑储气设备、P2G 设备,以及电、气负荷综合需求响应能够显著提升气电联合系统的可靠性,保证系统的安全运行。
由于场景⑦仍存在电、气负荷削减现象,在场景⑦的基础上进一步提升需求响应比例,得到需求响应对电力、气量不足期望值贡献系数指标的变化情况如图4 所示。从图4 可以看出,随着电、气负荷需求响应比例的提高,需求响应对电力、气量不足期望值贡献系数相应提高,当需求响应比例达到一定值,需求响应对电力、气量不足期望值贡献系数达到100%,由式(33)、(34)可知,此时系统的REENS、REGNS均为0,系统不会出现负荷削减,若再增大需求响应比例则RCDREE、RCDREG将维持不变。因此,合理安排需求响应比例,能够有效避免系统出现失负荷现象。
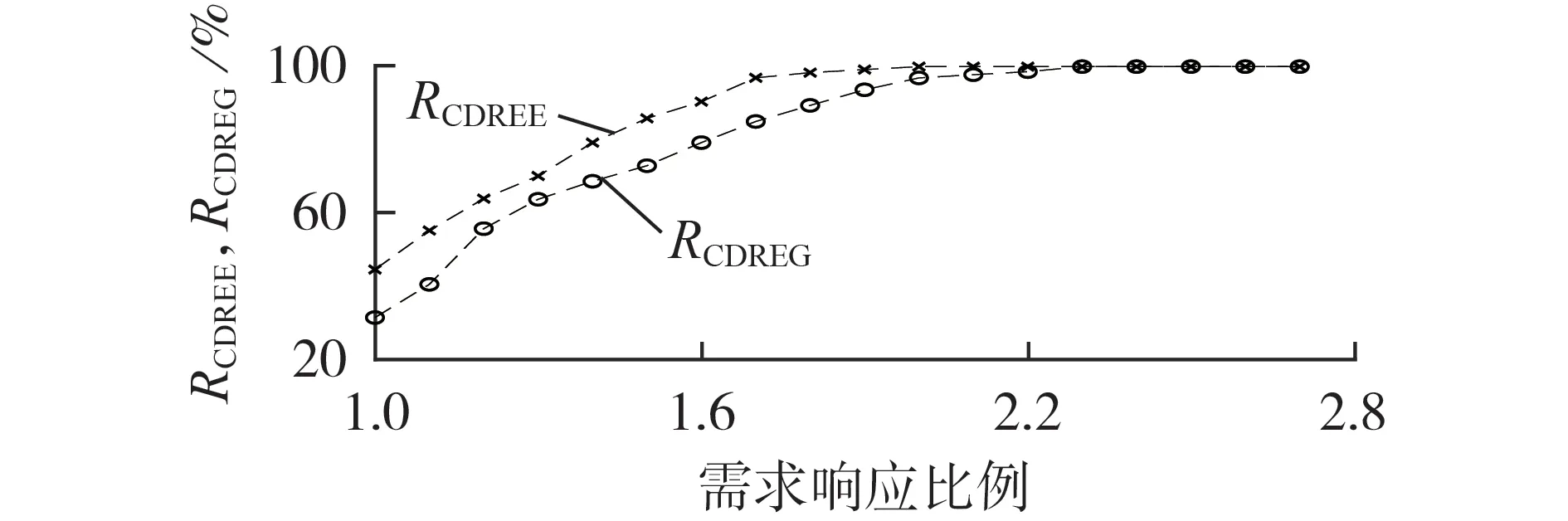
图4 需求响应贡献系数指标随需求响应比例变化趋势Fig.4 Tendency of contribution coefficient indexes of demand response with different demand response proportions
此外,为测试风电机组所在节点位置对系统可靠性的影响,在场景⑦的基础上,改变位于节点1、2的风电机组位置,得出的可靠性指标计算结果如表5 所示。由表可知,风电机组接入位置会影响电力系统可靠性,但基本不会影响天然气系统可靠性。在节点3、4 接入风电机组,系统切电负荷概率指标RLOELP和系统电力不足期望值指标REENS最小,系统的可靠性最高。因此,合理选择风电机组的接入节点,能够在一定程度上提升气电联合系统的可靠性。
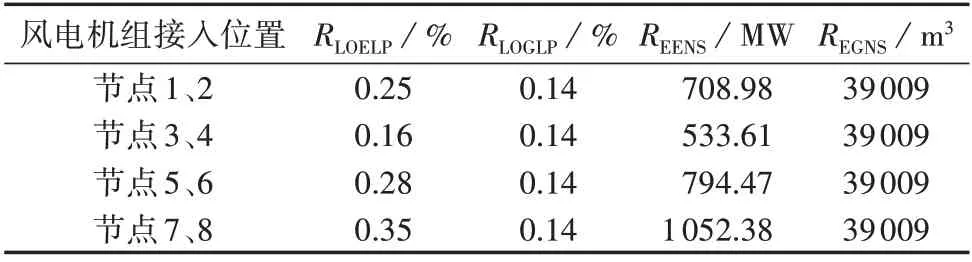
表5 不同风电机组接入位置下系统的可靠性评估指标Table 5 Reliability evaluation indexes of system under different connection locations of wind turbine units
4 结论
本文建立了考虑电、气负荷综合需求响应的气电联合系统负荷削减优化模型,提出了考虑综合需求响应的气电联合系统可靠性评估指标和方法,为提高模型求解效率,利用泰勒级数展开法对约束条件中的天然气潮流方程进行线性化处理。通过算例仿真分析,验证了本文所提模型、指标和方法的有效性。分析算例结果可得如下结论。
1)在相同的求解精度下,泰勒级数展开法的求解效率高于分段线性化法;合理设置泰勒级数展开的气压断点数,既能够保证气电联合系统负荷削减优化模型和可靠性指标的精确求解,又能够有效提高求解效率。
2)电负荷需求响应能在一定程度上改善天然气系统可靠性,气负荷需求响应能在一定程度上改善电力系统可靠性,两者具有互济性;相比单一需求响应,电、气负荷综合需求响应对气电联合系统可靠性指标的改善更显著,能够更有效地提升系统可靠性,保证系统运行安全性。
3)需求响应对系统可靠性的影响与需求响应的比例有关,合理协调各类型负荷需求响应比例、灵活中断和转移各类型负荷对系统的安全运行具有现实意义。
附录见本刊网络版(http://www.epae.cn)。

