改进果蝇优化算法的磁流变发动机悬置振动控制策略研究

申玉瑞，华德正，王宁宁，刘晓帆，刘新华,3

(1.中国矿业大学 机电工程学院， 江苏 徐州 221116；2.中国煤炭教育协会， 北京 100713； 3.姜堰经济开发区科创中心， 江苏 泰州 225500)

随着现代汽车设计朝着小型、大功率发动机方向发展，以及轻量化材料的开发使用，汽车噪声逐渐成为不可忽视的一大问题，而引起汽车噪声的主要来源之一便是动力总成。发动机悬置系统可有效抑制动力总成本身的振动及动力总成向车身传递的振动，从而提高汽车乘坐舒适性[1]。发动机液压悬置分为被动式液压悬置、主动式液压悬置和半主动式[2]液压悬置3种。其中，被动式液压悬置利用流体的粘性和惯性效应来满足大动态范围的刚度要求[3]，因此被动式液压悬置在低频共振区可以表现出良好的控制性能，但在非共振和高频区域的表现较差。主动式液压悬置可以在不同工作要求下提供良好的隔振效果，但其复杂的结构、较高的能耗和成本限制了主动式液压悬置在工业领域的广泛应用。而半主动式液压悬置在有效避免两者缺点的同时，又兼具了两者的优点，因此本文采用半主动式液压悬置[4]，具体地说，是一种基于磁流变液的半主动式液压悬置[5-7]。

磁流变液是一种固-液两相智能材料，其表观粘度可随外加磁场的变化而变化。磁流变液自问世以来，研究人员对磁流变液本身特性及在汽车工业等多领域的潜在应用进行了大量研究。就应用角度而言，磁流变液主要应用于振动控制部件或者系统：汽车悬挂系统[8-9]、驾驶员座椅悬挂系统[10]、桥梁振动[11]、建筑隔震[12]、其他柔性结构[13]。然而，由于磁流变液磁性颗粒的磁滞现象及流体的滞后特性等原因，使磁流变液具有强非线性特性，因此需要建立一种可预测的控制方法，以保证磁流变悬置快速准确地响应和动作。

PID控制器以其控制效果显著、控制简单、适用范围广等优点，在工业中得到了广泛应用。胥良等[14]采用基于神经网络算法改进非线性PID控制，对矿井提升机的控制策略进行了研究。此外，还有采用自适应模糊控制[15]、蜻蜓算法[16]、神经网络[17]和遗传算法[18]等对PID参数进行调整。研究结果表明，与这些算法相结合的控制器相较于传统的PID控制器其控制效果有着明显的提升。然而随着人们对控制效果要求的提高，简单地将优化算法应用于PID控制器已经不能满足需求，于是改进算法成为了研究人员的热点研究方向之一。Tavakoli 等[19]提出了一种带PID开关面的自适应自整定PID模糊滑模控制器，并用于抑制电力系统振荡。Sheng 等[20]将FOA用于调整电子节气门的分数阶模糊PID控制器的参数。Li等[21]提出了一种新的改进的飞行优化算法(MFOA)来确定PID控制器参数，仿真结果表明：MFOA-PID控制器优于FOA-PID控制器。Tian等[22]提出了另外一种改进的果蝇优化算法，采用一种新的惯性权函数，通过动态调整搜索范围来平衡全局搜索和局部微调。李强等[23]设计了微重力环境下的磁流变传动装置，提出了一种自适应模糊PID控制策略，有效减小了传动系统的速度波动，提高了运动稳定性。

基于以上研究，本文以磁流变发动机悬置系统为研究对象，首先，分别建立其参数化动力学模型与非参数化动力学模型。通过简化悬置系统结构建立其动力学方程；利用神经网络算法建立磁流变发动机悬置的正向、逆向非参数化辨识模型。其次，将改进的果蝇优化算法(IFOA)应用于磁流变悬置PID控制器的参数调整，从而提高磁流变发动机的隔振性能，有效降低车身的振动位移和振动加速度。最后，建立相应的动态特性实验和振动控制仿真实验以验证所提控制策略的有效性。

1 磁流变发动机悬置系统模型

1.1 磁流变发动机悬置参数化动力学模型

发动机在空间表现为6自由度的受约束系统，经由多个具有三向刚度和阻尼的悬置支承安装在车架上。现代悬置系统设计方法已经能在很大程度上实现振动系统各阶模态的解耦[24]。因此，仅研究磁流变发动机悬置在垂直方向上的阻尼可控，且不考虑路面不平度的输入。如图1所示，将发动机悬置系统简化为垂直方向的单自由度系统模型。

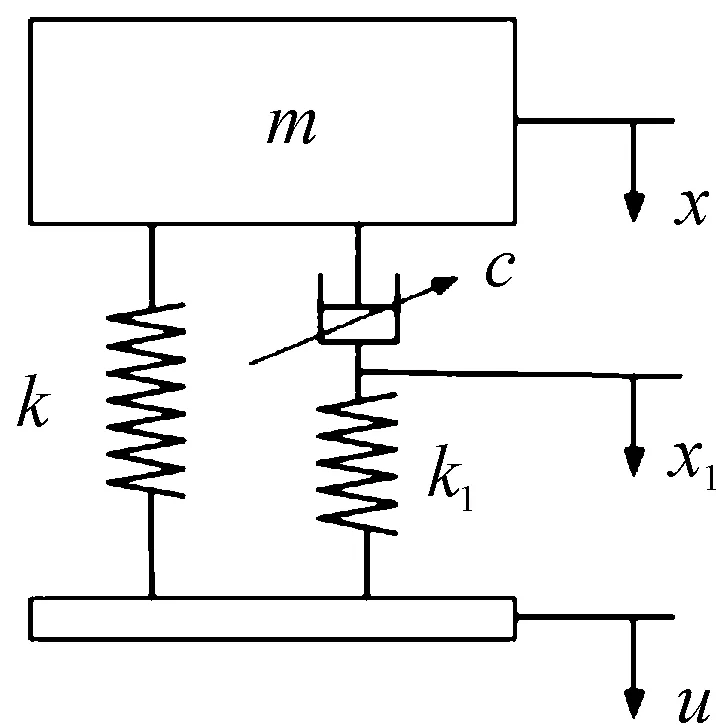
图1 悬置系统垂直方向动力学模型示意图

如图1所示，动力总成的质量和位移分别为m、x，悬置系统在垂直方向上的刚度为k，磁流变液压悬置的等效阻尼由弹性系数k1的弹簧和粘性阻尼系数c的麦克斯韦单元表示。车架的位移为u，悬置与附加弹簧连接点的位移为x1。对其进行动力学分析：

(1)

1.2 磁流变发动机悬置非参数动力学模型

神经网络可以通过输入的数据进行大量的模拟训练，在大量学习的基础上可以逼近目标函数，因此利用Elman神经网络来建立磁流变悬置的非参数动力学模型。设计磁流变悬置动态特性实验以获得神经网络所需的训练数据。取激振频率为15 Hz，振幅为5 mm，分别施加0.5、1.5、3 A的电流，所建立的磁流变悬置动态特性实验装置如图2所示。

图2 动态特性实验装置图

1.2.1磁流变发动机悬置正向模型

如图3所示，磁流变悬置正向模型将上一时刻的位移xk-1、速度vk-1、电流Ik-1、阻尼力Fk-1和当前时刻的位移xk、速度vk、电流Ik和激振频率fk作为神经网络的输入，当前时刻的输出阻尼力Fk为神经网络的输出，D表示延迟时间。

图3 磁流变悬置正向模型示意图

为了定量评价所建立磁流变悬置正向模型的预测精度，建立评价指标如下：

(2)

式中：EF为正向模型预测精度；Fk为实验中实际测得的输出阻尼力；Fk′为所建立磁流变悬置正向模型的输出阻尼力；nL为测试样本的个数。

0.5、1.5、3 A激励电流条件下的磁流变发动机悬置的阻尼力和位移值如图4所示。图中动态特性实验所测得的数据用实线表示，磁流变悬置正向模型的预测结果用虚线表示。

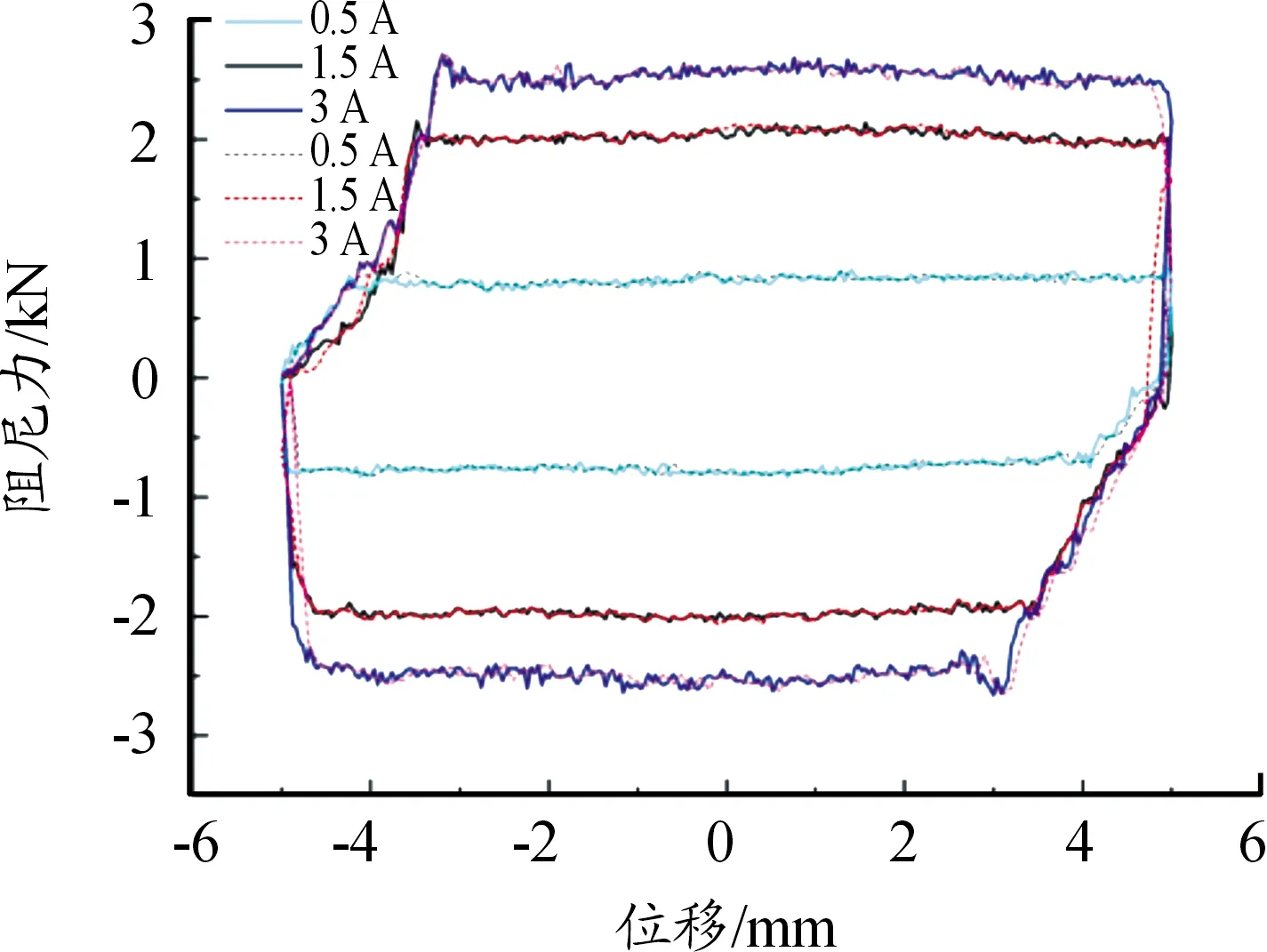
图4 悬置正模型辨识结果曲线

不同激励条件下磁流变悬置神经网络正模型对悬置阻尼力的预测精度如表1所示。

表1 磁流变悬置正向模型的预测精度

从图1和表1的结果可以看出：所建立的磁流变悬置正向模型的预测结果与磁流变发动机悬置动态特性实验的数据在整体上具有相同的变化趋势，且其预测精度普遍高于95%，进一步证明了正向模型的有效性。

1.2.2磁流变发动机悬置逆向模型

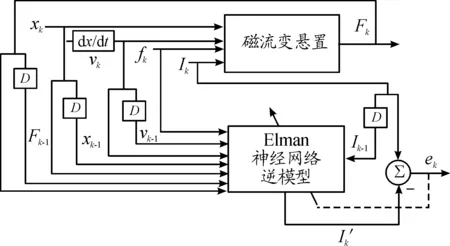
图5 磁流变悬置逆向模型辨识过程框图

为了定量评价所建立磁流变悬置正向模型的预测精度，同样建立评价指标：

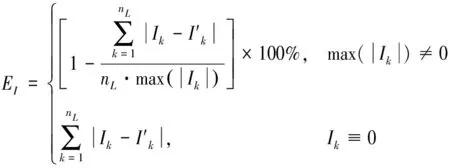
(3)

动态特性实验中实际输入电流与磁流变悬置逆向模型的预测结果如图6所示，图中动态特性实验所测得的数据用实线表示，磁流变悬置正向模型的预测结果用虚线表示。磁流变悬置逆向模型的预测精度如表2所示。

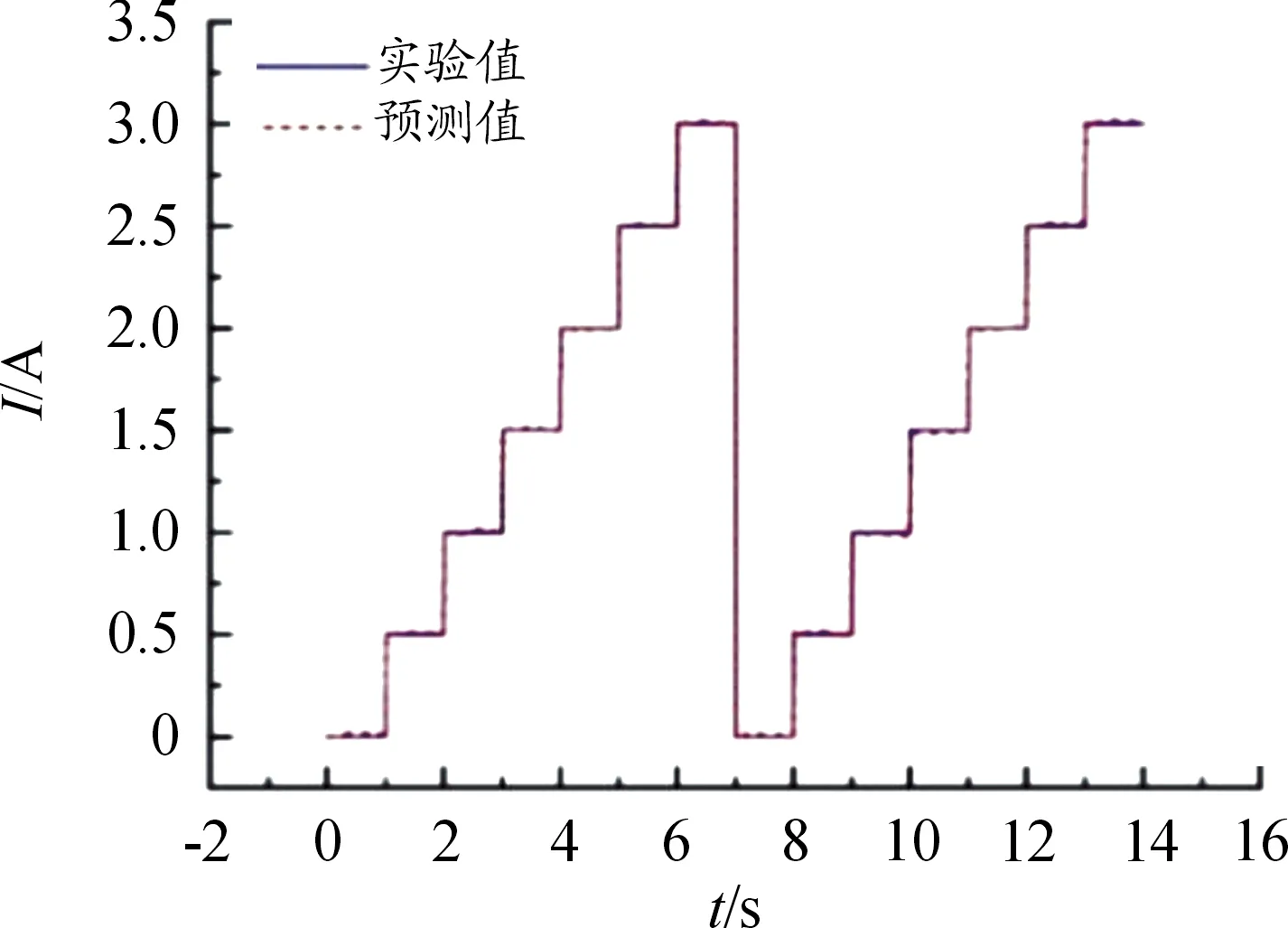
图6 悬置逆模型辨识结果曲线

表2 磁流变悬置逆向模型的预测精度

从图6和表2的结果可以看出：所建立磁流变悬置逆向模型辨识的电流大小与磁流变悬置动态特性实验过程中所施加的电流大小基本一致，其预测精度最低为98.10%，最高为99.82%。表明该逆模型具有较高的可靠性，这为磁流变悬置的半主动控制提供了先决条件。

2 控制策略

2.1 神经网络PID

图7 神经网络PID原理框图

2.2 改进果蝇优化算法

FOA是一种基于果蝇觅食行为的全局智能优化算法，更适合于复杂问题的优化。基本FOA的步骤可以表示如下[25]：

步骤1随机初始化果蝇数量P、最大迭代次数INmax、随机距离FR和初始位置(Xaxis,Yaxis)。

步骤2赋予果蝇个体飞行的随机方向Randi和距离FR。

(4)

步骤3计算果蝇个体与原点之间的距离Disti和味道浓度判别值Si。

(5)

Si=1/Disti

(6)

步骤4将味道判别值Si代入适应度函数，求出果蝇个体的味道浓度Smelli，找出种群中浓度最优的果蝇。

Smelli=Function(Si)

(7)

[bestSmell,bestindex]=min(Smell)

(8)

步骤5保留最优值Smellbest，果蝇群体飞往最优位置。

Smellbest=bestSmell

(9)

(10)

步骤6迭代寻优，重复步骤4～6，直至达到预设精度值。

从基本果蝇优化算法可以看出，飞行距离的参数分配很大程度上依赖于Randi函数，由于盲目搜索，极有可能陷入局部极值。因此采用云模型算法对果蝇优化算法的随机方向函数进行自适应调整，改进后的果蝇优化算法流程如图8所示。

图8 改进果蝇算法流程框图

当获得每只果蝇个体位置信息后，首先使用逆向云发生器将定量的果蝇个体信息数据转换成定性概念的数字特征。随后将原始果蝇种群X1，X2，…，Xn随机分成m组，每组q只果蝇(n=m×q且n，m，q都是正整数)。分别计算每组果蝇的组内样本方差：

(11)

(12)

最后使用正向云发生器，得到n个云滴及其确定度：

μ(x)=Randi=exp(-(Xi-Ex)2/2(Yi)2)

(13)

其中，Yi～N(En,He)，Xi～N(Ex,Yi)

(14)

He2=EY2-En2

(15)

(16)

(17)

2.3 基于改进果蝇优化算法的PID控制方法

基于IFOA的PID控制原理如图9所示。首先基于云模型改进的果蝇优化算法(IFOA)将获得的原始果蝇种群的信息Xi、Yi发送给逆向云发生器，得到果蝇种群的Ex、En、He；再经由正向云发生器得到Randi来迭代果蝇位置；最后将IFOA优化的PID控制器的3个参数作用于磁流变悬置，从而实现对输入电流的半主动控制。

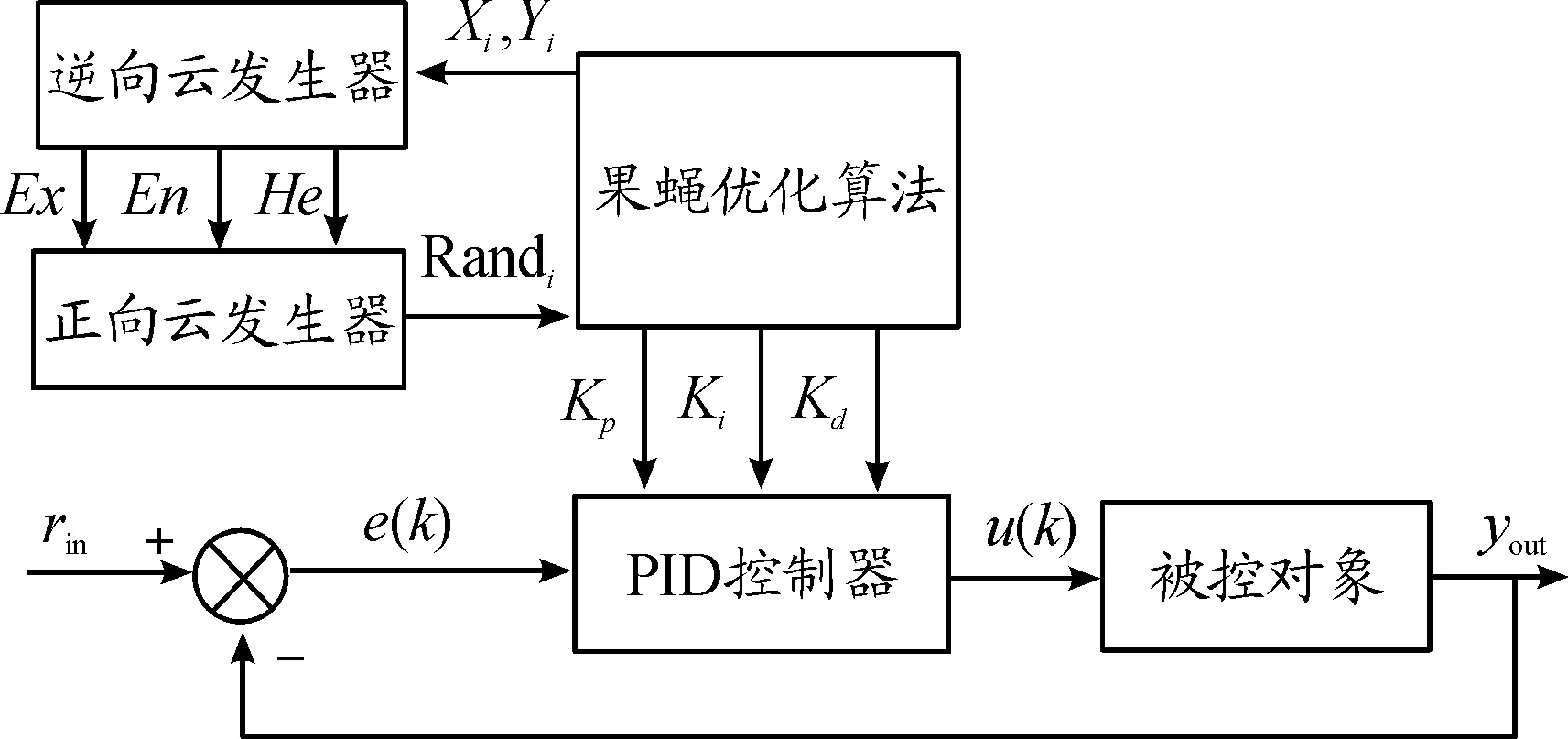
图9 基于IFOA的PID控制原理框图

3 磁流变发动机悬置半主动控制系统实验研究

3.1 电流控制实验

由于磁流变液的强非线性特性以及实际使用过程中不可预测的复杂多变的使用环境，对磁流变发动机悬置系统的半主动控制的关键是根据不同的工况、不同的振动阻尼需求对磁流变悬置上的输入电流进行相应的调整，进而达到减振的目的。实验中通过LabVIEW向DP811A直流电源传送信号。因此，检验磁流变液悬置减振效果优劣的先决条件是检验输出电流准确性与否。利用LabVIEW软件平台进行振动分析和电流控制，如图10所示。

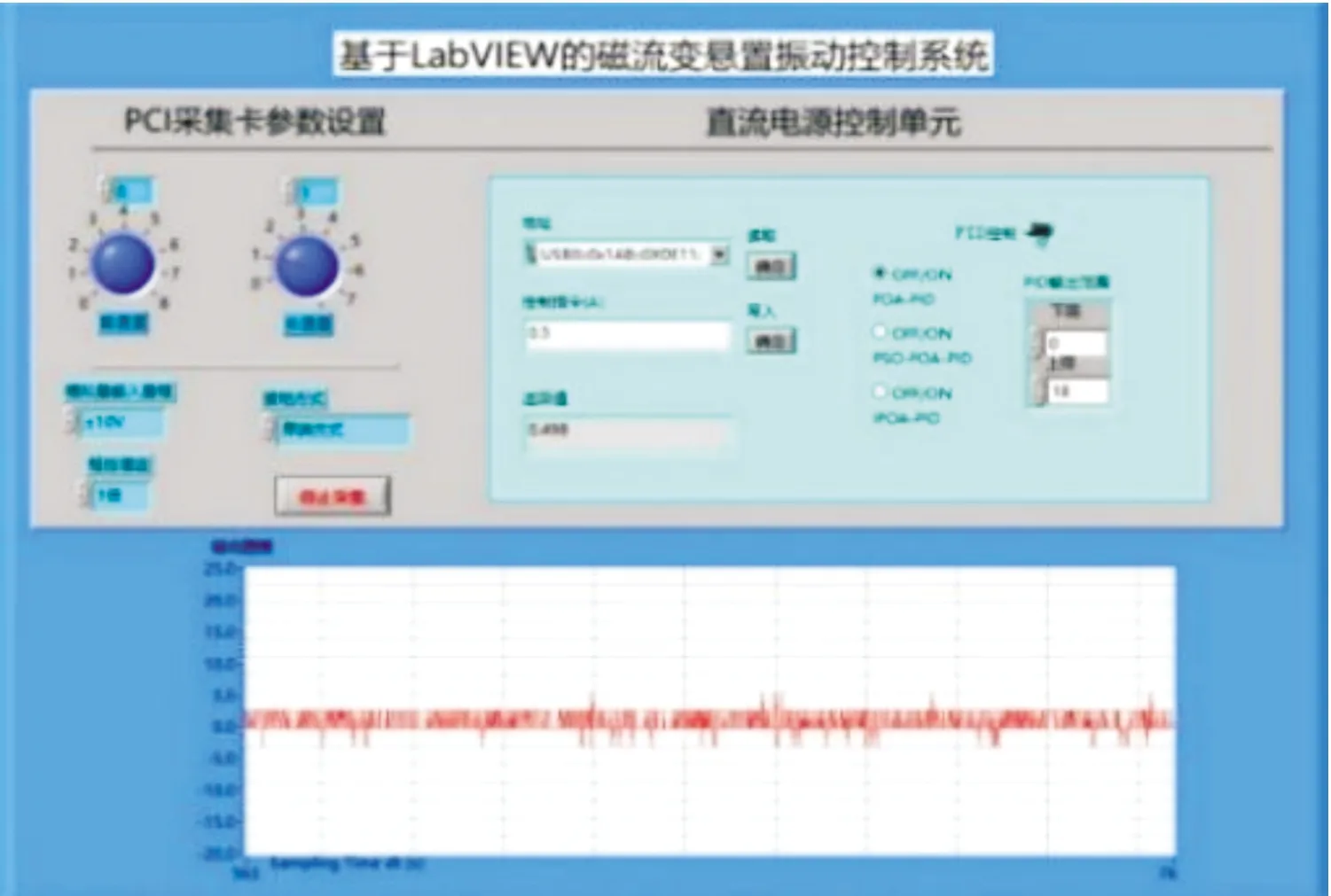
图10 磁流变发动机悬置控制系统界面

先后通过LabVIEW向可编程电流源发出0.5、2 A的输出电流命令，实验结果如图11所示。可以看到，直流电源与LabVIEW电流控制模块的通讯完好，输出电流总体上保持着0.5、2 A的恒定输出。但是从局部放大图可以看到，实际输出电流存在一定的上下波动。对其结果进行分析，输出电流的平均偏差为7.538e-0.3，相对平均偏差为1.499 8%，误差的峰峰值为0.014 1 A，输出电流的稳定性为后续试验奠定了基础。

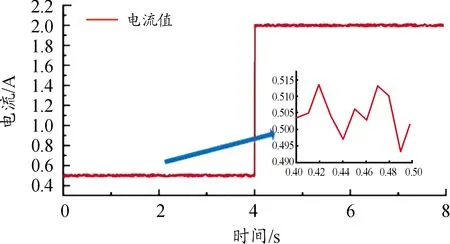
图11 电流控制实验结果曲线

3.2 磁流变悬置隔振性能实验

为验证所设计的磁流变悬置和控制算法的可靠性以及测试磁流变悬置的隔振效果，搭建磁流变悬置系统的振动控制实验台如图12所示。部分实验设备型号如表3所示。

图12 磁流变悬置控制系统实验台实物图

表3 实验设备型号

首先上位机发出电流信号通过变频器让振动电机模拟汽车发动机自身的简谐运动，分别模拟转速n=890 r/min和转速n=298 0 r/min 2种工况下的工作状态。振动信号通过振动台传递给磁流变悬置，其振动信号包括振动位移和振动加速度通过传感器实时采集。最后分别对FOA、PSO-FOA[26]和IFOA控制的磁流变悬置系统进行半主动控制实验，并分别对FOA、PSO-FOA和IFOA的实验结果进行比较。

在不同控制算法下，发动机悬置系统的性能指标测试曲线如图13所示。可以看出，低频时，由IFOA-PID算法控制的悬置系统的位移和加速度表现明显优于其他2种控制算法，其位移与加速度值最小、振幅最小；高频时，由IFOA-PID算法控制的悬置系统的位移与加速度控制效果也优于其他2种控制算法。此外，如图13(d)所示，FOA-PID算法控制的磁流变悬置系统在1.8～2.2 s时加速度出现了明显的波动，PSO-FOA-PID算法在0.5～1 s时加速度值也发生了同样的剧烈变化。反观IFOA-PID算法控制的高频加速度相较于自身加速度值虽有较为明显的数值变化，但显然受到了明显抑制，这进一步表明了所提算法的优越性。

图13 磁流变悬置振动测试曲线

为了更进一步地对实验结果进行分析，更定量化地表示3种算法的控制效果。如表4所示，分别计算了3种算法控制的磁流变悬置系统振动加速度和位移均方根值(RMS)。

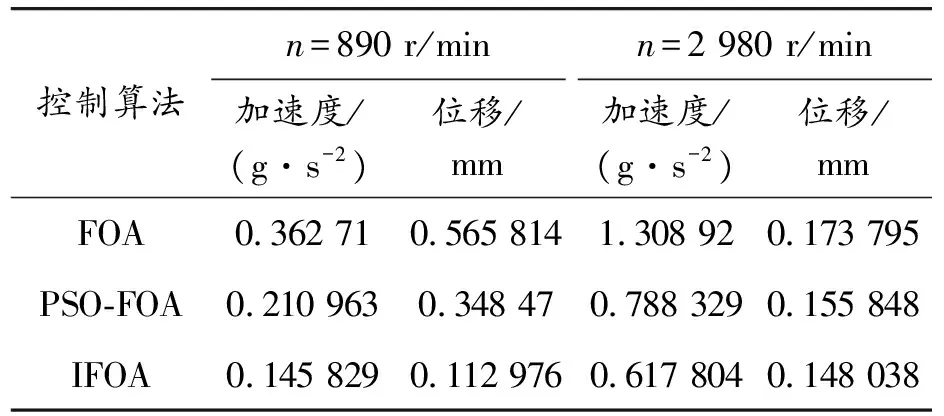
表4 不同频率的均方根

通过计算，IFOA-PID算法控制的磁流变悬置系统的低频加速度均方根值和位移均方根值分别为0.145 829 g·s-2、0.112 976 mm，其高频加速度均方根值和位移均方根值分别是0.617 804 g·s-2、0.148 038 mm。与FOA-PID相比，其低频加速度与位移均方根值、高频加速度与位移均方根值分别减少了59.794 6%、80.033 0%、52.800 4%、14.820 3%；与PSO-FOA-PID相比，其低频加速度与位移均方根值、高频加速度与位移均方根值分别减少了30.874 6%、67.656 9%、 21.631 2%、5.011 3%。

4 结论

1) 相比传统发动机悬置，磁流变发动机悬置表现了更优越的控制效果和更好的隔振性能。

2) 基于Elman神经网络建立的磁流变悬置正向、逆向辨识模型表现可靠，其辨识精度可达95%以上，增大训练样本种类与数量可进一步提高辨识模型的预测精度。

3) 文中提出的基于云模型改进果蝇优化算法的PID控制策略在振动位移和振动加速度的控制效果上表现出了明显的优势，可有效抑制发动机悬置系统的振动。