等离子体激励控制圆柱绕流的大涡模拟研究

赖晨光，付 航，凌志伟，贾 浩，周毓婷

(1.汽车零部件先进制造技术教育部重点实验室(重庆理工大学)， 重庆 400054；2.重庆理工大学 车辆工程学院， 重庆 400054)

圆柱绕流问题是流体力学的经典问题，蕴含了丰富的流动现象和机理，一直是空气动力学、水动力学和风工程领域中的重点研究问题[1-3]。针对此问题，许多研究者提出了各种流动控制方法，如以被动控制为主的添加附属杆[4]、分隔板[5]、涡流发生器[6]和在圆柱表面开细缝[7]等，和以主动控制为主的移动附面层[8]、吹吸气[9]、合成射流[10]、电磁控制[11]等。

近些年来，等离子体主动流动控制由于其结构简单、能耗低、响应快等优点深受各国研究人员的关注[12]。等离子体是除固体、液体和气体之外的物质第四态。等离子体由大量的电子和离子所组成，其整体呈电中性，并且其运动主要受电磁场力的支配，从而表现出显著的集体性行为[13]。由于非对称布置表面介质阻挡放电(surface dielectric barrier discharge，SDBD)产生的等离子体较均匀，控制效果较好，利用其进行流动控制是目前最常用的方法，其结构如图1所示[14]。电极由绝缘介质层隔开，非对称布置，上电极接电源正极，下电极接电源负极，当电压达到某一定值时，上电极右端空气被电离，产生稳定的等离子体，从而诱导流体加速流动。

图1 SDBD结构示意图

国内外各研究人员使用等离子体主动流动控制技术抑制气流流动分离，从而达到改善控制对象气动特性的目的[15-17]。更有不少学者对等离子体气动激励控制圆柱绕流流动分离做了相关实验研究[18-20]，从公开文献看，其大多数研究都只考虑了在特定来流条件以及固定激励器位置时的控制效果，并且利用数值模拟方法研究等离子体激励对圆柱绕流尾流区流场结构的影响也相对较少。

综上所述，基于Suzen等[21]提出的等离子体唯象学模型，通过Fluent仿真软件中的用户自定义标量(UDS)求解电势分布和电荷密度分布方程，并将得到的等离子体体积力以动量源项的形式耦合到大涡数值模拟控制方程中，从而探究等离子体气动激励对三维圆柱绕流流动分离的控制效果，同时分别考虑不同来流雷诺数和等离子体激励器激励位置对控制效果的影响，最后对控制前后圆柱绕流流场结构的变化进行了分析。研究结果对应用等离子体对圆柱绕流流场进行主动流动控制，从而实现减阻降噪具有一定指导意义。

1 数值模拟方法

1.1 控制方程

由于在三维圆柱绕流中其尾流区存在复杂的三维涡结构，为了更加精确地捕捉到其流动细节，将采用大涡数值模拟方法进行数值模拟计算。而大涡模拟的基本思想是使用一个滤波函数将流场中的大、小尺度的湍流脉动分隔开来，大尺度脉动可以通过湍流模型直接进行计算，而小尺度脉动将使用亚格子应力模型计算其对大尺度脉动的作用。大涡模拟控制方程为：

(1)

(2)

由于可以将等离子体激励对流体的作用效果等价于等离子体放电产生的电动体积力对流体的作用效果，忽略其放电过程。因此，将等离子体气动激励产生的体积力耦合到大涡模拟控制方程中：

(3)

(4)

1.2 等离子体唯象学模型及其验证

要得到等离子体对流体的作用效果，需要计算由等离子体放电所产生的电动体积力大小。在忽略电磁场力的条件下，单位体积的体积力可以近似表示为：

(5)

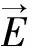
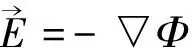
(6)

由高斯定律得：

▽·(ε▽Φ)=-ρc

(7)

其中ε为介电常数。

由于气体粒子是被弱电离的，可以认为总电势Φ由两部分组成：一部分由外部电场产生的电势φ，另一部分由等离子体中净电荷密度产生的电势φ，即：

Φ=φ+φ

(8)

因此，可由2个电势分别写出2个独立的方程，一个是由于电极上所加电压产生的外部电场：

▽(ε▽φ)=0

(9)

另一个是带电粒子产生的电场：

(10)

其中λD是德拜长度，方程(10)的详细推导请参见文献[21]。通过求解方程(9)(10)即可得到电荷密度ρc和电势φ，从而由方程(5)得到等离子体作用下的电动体积力。

通过对比在静止空气中等离子体诱导流场的实验流线及数值模拟流线，对数值方法进行了校准，如图2所示。从实验流线图可以观察到，在等离子体作用下，流体被吸入到植入电极上方表面区域中，并以射流的形式在大约1 m/s的速度下向下游发展，所得到的速度流线与文献[17]的实验结果和文献[21]的仿真结果都吻合。这表明本文对等离子体诱导流体流动仿真的准确性，并说明该模型可以应用到等离子体控制圆柱绕流流动分离的数值模拟计算中。

图2 等离子体在静止空气中诱导的速度流线图

1.3 几何模型与求解域

圆柱几何模型如图3(a)所示，圆柱直径为50 mm，厚为10 mm，展向宽度为πD。图3(b)展示了等离子体激励器安装在圆柱表面的位置，使用从圆柱前驻点到暴露电极最右端的圆弧所对应的圆心角θ表示其位置。在圆柱表面上下对称各布置一对等离子体激励器，激励器轴向宽度为10 mm，展向宽度与圆柱展向宽度相等，激励器厚为0.1 mm，暴露电极与植入电极轴向间距为0.5 mm，纵向间距(绝缘介质层厚度)取0.1 mm。

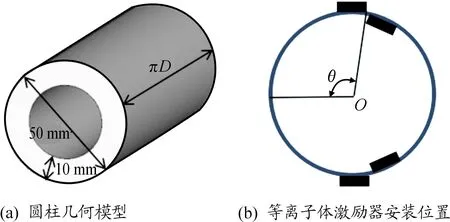
图3 圆柱几何模型和等离子体激励器安装位置示意图

数值模拟的计算域如图4所示，其中D为圆柱的直径。为了使流体流动充分发展，计算域的长和高分别取20D和10D，圆柱中心距离计算域入口与出口分别为5D与15D，圆柱中心距离上下边界均为5D。由于本文探究的是无限长三维圆柱绕流且Re均在亚临界区内，其流场均呈现三维特性，而当计算域展向宽度取πD时，就能体现出圆柱绕流的三维效应[22]，所以计算域宽度与圆柱的展向长度一致，均取为πD。

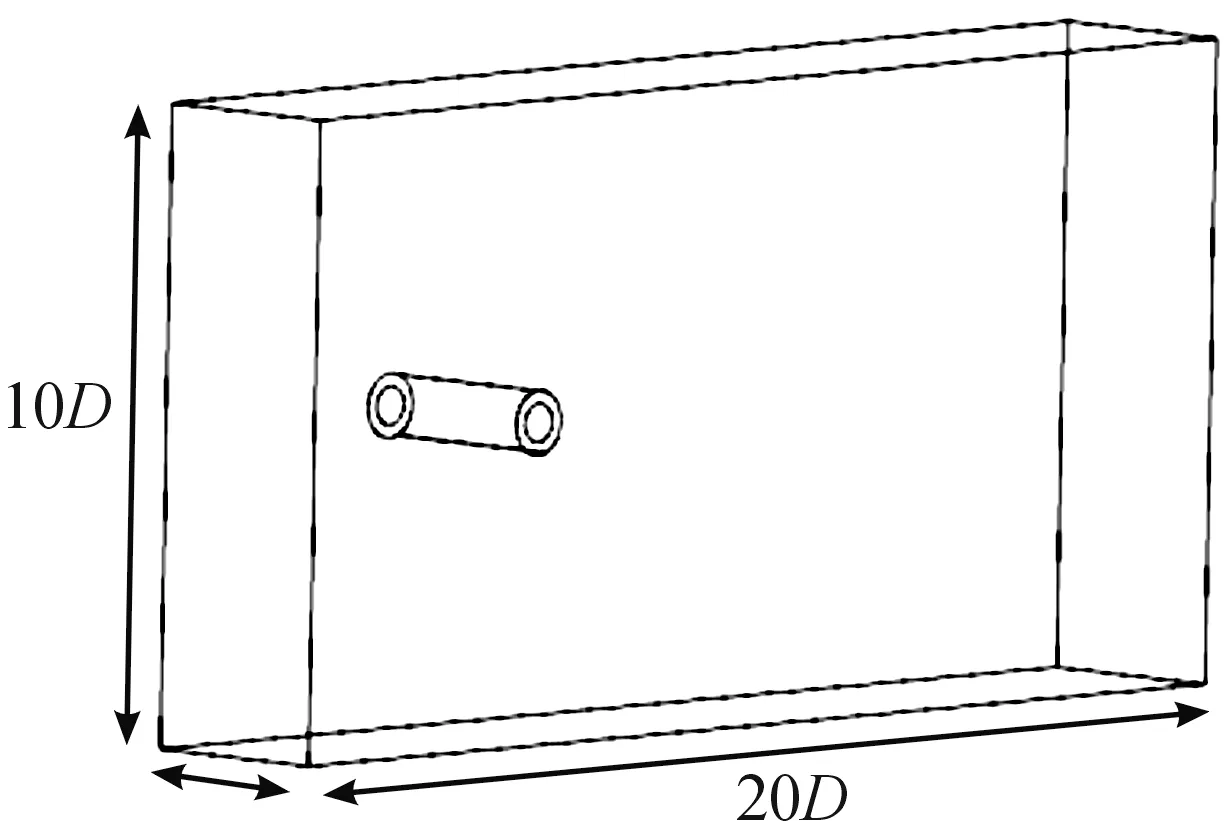
图4 流体计算域示意图

1.4 计算网格

数值计算的网格使用分块结构化网格进行划分，网格划分细节如图5所示。圆柱周围采用O型结构化网格，这能保证圆柱周围生成正交性良好的结构化网格，提高其网格质量，对圆柱近壁面区域的网格进行局部加密，使能更好地模拟其流动细节，同时保证边界层内第一层网格的y+≤1。不同雷诺数Re=3 900、10 000、20 000和30 000近壁处第一层网格厚度Δy=0.001D、0.000 5D、0.000 1D和0.000 05D。网格总数均保持在400万左右。

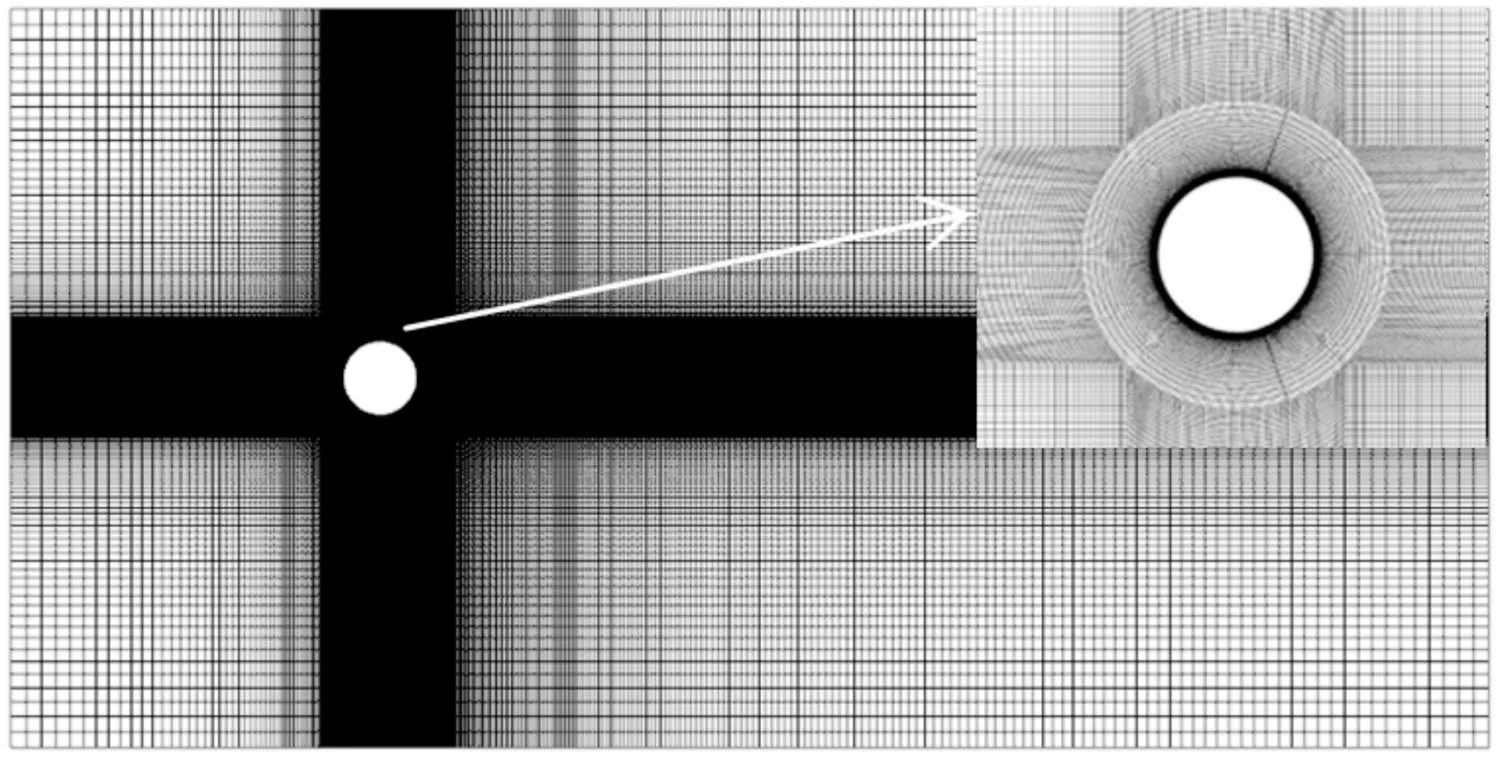
图5 网格划分细节示意图

1.5 边界条件与求解设置

设置的边界条件如表1所示，计算域入口为速度入口，速度大小分别设置为U∞=1.14、2.92、5.84和8.76 m/s，对应不同的雷诺数3 900、10 000、20 000和30 000，计算域出口为压力出口，参考压力为大气压，圆柱表面设置为无滑移壁面边界条件，其他边界均设置为对称壁面边界条件。数值求解方法采用SIMPLE算法，空间离散采用有界中心差分格式，时间离散采用隐式有界2阶差分格式，时间步长均取0.001 s。

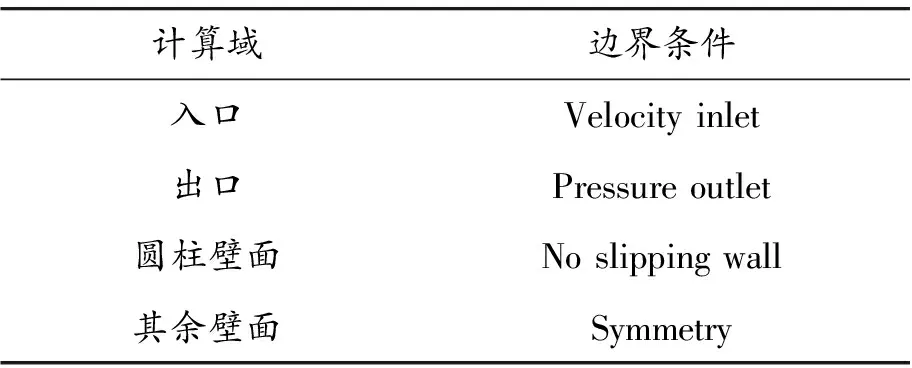
表1 边界条件

1.6 数值方法验证

为检验计算方法的可靠性，利用上述方法对未施加等离子体激励的圆柱绕流流场进行计算。待计算稳定后，对相关参数进行采样，并将采样得到的斯特劳哈尔数St、平均阻力系数Cd等流场特征参数与文献[23]的实验结果进行对比。特征参数St和Cd定义式分别如下：

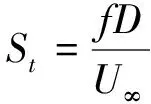
(11)

(12)

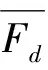
图6为在不同雷诺数下未加等离子体激励的平均阻力系数和斯特劳哈儿数与以往实验值的比较，可以清楚地看到数值模拟结果与实验值吻合较好，说明所采用的数值模拟方法具有可靠性，这为研究施加等离子体激励的控制效果奠定了基础。

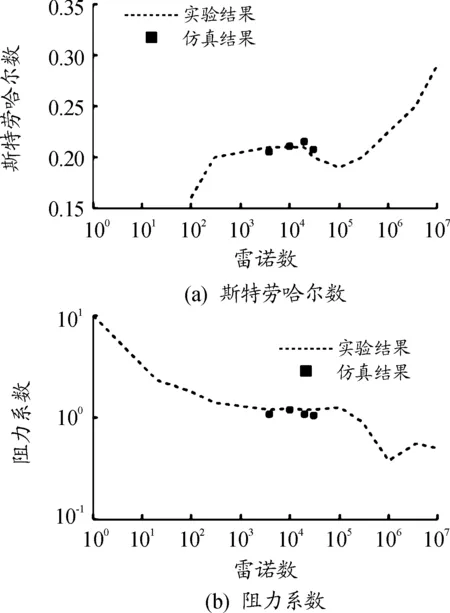
图6 斯特劳哈尔数、阻力系数随雷诺数的变化曲线

2 计算结果及分析

为了探究来流雷诺数和激励器安装位置对控制效果的影响，保持等离子体激励器激励参数不变。而根据文献[24]的实验结果，激励电压是影响等离子体控制效果最主要的参数，其值越大，等离子体控制能力越强，即等离子体诱导流体的流速越大，但当达到18 kV后，等离子体激励器放电将会达到饱和状态，此时诱导流速会趋于一个相对稳定的值(3 m/s左右)。而激励频率几乎对平均最大诱导流速没有影响，所以为了得到较好的控制效果，激励电压取18 kV。

2.1 无控制状态下圆柱绕流流场特性分析

图7给出了Re=3 900、10 000、20 000、30 000情况下z=0处截面的平均流向速度云图。由图7可直观地看出圆柱体尾流区流场结构。气流在受到圆柱前端阻挡后沿着圆柱表面向下游发展，并发生了明显的气流分离现象，最终导致在圆柱尾部形成一个明显的速度回流区，这是导致圆柱产生较大阻力的主要原因。而随着来流雷诺数的增加，即来流速度增大，回流区的速度也相对增大。

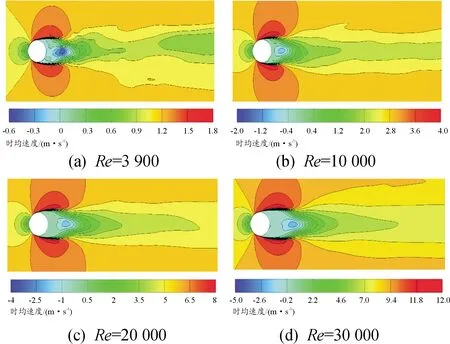
图7 平均流向速度云图(z=0)

2.2 不同来流雷诺数对控制效果的影响结果分析

为了对比在不同来流雷诺数下等离子体激励的控制效果，保持等离子体激励器安装位置一致，从圆柱前驻点开始，顺时针方向为正，如图3(b)所示，取θ=90°。图8给出了等离子体激励控制前后三维圆柱绕流升阻力系数变化曲线，从图中可以清楚地看到在相对较低来流雷诺数下施加一定等离子体激励强度对圆柱绕流都有一定的控制效果，特别是在来流雷诺数为3 900的情况下，平均减阻率达到了63.65%，升力的上下波动幅度也有所减小。在来流雷诺数为10 000和20 000的工况下，等离子体的控制效果也比较好，相对于来流雷诺数为3 900的工况控制效果有所减弱。当来流雷诺数增加到30 000时，几乎没有明显的控制效果。这说明随着来流雷诺数的增加，等离子体的控制效果会逐渐减弱。

图8 升阻力系数变化曲线

由于篇幅有限，仅选取了Re=3 900与Re=30 000两个典型结果进行流场分析。图9显示了在2种来流雷诺数情况下未施加等离子体激励与施加等离子体激励的圆柱绕流流场的平均流向速度云图。在Re=3 900情况下，可以看出施加了等离子体激励的圆柱尾部的流动分离明显得到抑制，相对与未施加等离子体激励的情况分离点向后推迟，尾部分离区也明显变小。造成这一结果的原因可能是在施加了等离子体激励后，产生的等离子体对近壁面气流有一个力的作用，进而诱导近壁面流体加速，增加了近壁面流体的动能，从而增强了边界层抵抗逆压梯度的能力。在Re=30 000情况下，等离子体激励的施加带来的影响并不如Re=3 900时效果那么明显，甚至可以说是微乎其微，这可能是由于随着雷诺数的增加，来流动能也相应增加，而当前激励参数下所产生的流动扰动能力有限，还无法对较高雷诺数流动造成明显的影响，如果想要在高雷诺数条件下得到明显的流动控制效果，需要优化等离子体激励器结构及参数从而提高其控制强度。

图9 平均流向速度云图

2.3 不同激励位置对控制效果的影响结果分析

激励器位置的安装也是影响其流动控制效果的一个重要参数。这里以3 900的来流雷诺数为基准工况，分别选取了3个激励位置，分别为θ=70°，90°，110°。图10给出了当Re=3 900时不同激励位置下的平均流向速度云图。

图10 平均流向速度云图

在将激励器位置前移至70°时，圆柱表面的流体分离点明显提前，并且圆柱尾部的回流区明显比激励位置为90°时更大，控制效果变弱。而将激励器位置后移至110°时，圆柱表面的流体分离点明显后移了，同时圆柱尾部的回流区相较于激励位置为90°得到进一步压缩，其控制效果明显要更好，这与之前的研究者得出的将激励位置尽量安装在流体分离点之前的位置相悖。造成这一结果的原因可能是在流动分离点前施加激励时，激励器周围气流的动能较大，其对周围的气流影响变弱，而在流动分离点之后施加激励时，激励器周围气流的动能较小，其对周围的气流影响会大一些。这说明在当前来流工况下，等离子体激励位置安装在靠近尾流区时有利于减小圆柱所受阻力。

为了更加直观地观察激励位置对圆柱尾流区的流场特征的影响，现取如图11特征位置所示近场直线进行流场分析，即x/D=1.06处平行于y轴的直线，直线范围是-3.0D～3.0D。图12给出了在Re=3 900情况下x/D=1.06处x方向的时均速度值。由图12可知，在90°位置施加了等离子体后，在圆柱尾部中心位置处速度损失减少，且速度恢复较快。将激励角度变为110°后，在圆柱尾部中心部位出现了速度增长区域，这可能是由于在等离子体激励作用下，主流核心区域的流体在等离子体诱导的作用下，与圆柱近壁面流体进行了参混，使近壁面流体动能增加，在到达圆柱后驻点之前，圆柱上下表面流体稳定地离开圆柱表面，并在圆柱尾流区中心横向轴处融汇，从而导致此处的流体流速出现增长。而将安放角度移动至70°后，速度的损失情况同原始模型几乎一致，但是损失速度的范围较原始模型有所改善。

图11 圆柱周围的特征位置示意图

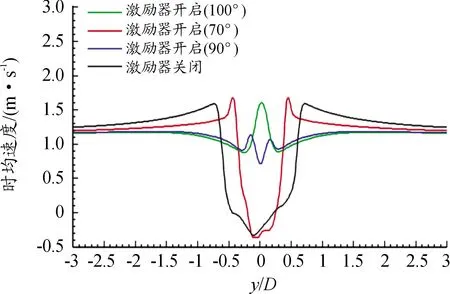
图12 x/D=1.06处时均速度曲线

3 结论

1) 在等离子体激励强度下，等离子体对圆柱绕流气动特性都有改善作用。

2) 当来流雷诺数增加时，等离子体控制效果明显减弱，要提高其控制效果，需增强等离子体控制能力。

3) 等离子体激励器安装位置对其控制效果影响明显，存在一个最佳控制位置。在相对较低的雷诺数下，将其安装在靠近圆柱尾流区时的控制效果明显好于安装在圆柱绕流气流分离之前的位置，具体原因还有待进一步深入研究。

本研究只探究了3 900雷诺数情况下的等离子体激励器安装位置对控制效果的影响，并未对相对较高雷诺数情况下的等离子激励进行位置比较研究。另外对于相对较高雷诺数的情况，使用多对等离子体激励器同时串联工作，是否会提高其控制效果，这些都是接下来需要去探究的内容。