基于SOA-BP神经网络的选择性激光烧结成型件精度预测模型

肖亚宁，郭艳玲，张亚鹏，王扬威，李 健

(东北林业大学机电工程学院，哈尔滨 150040)

选择性激光烧结是一种基于实体三维模型，然后利用高能量激光束逐层烧结堆积成型的快速成型技术之一[1]。相比传统的加工制造技术，其使用的成型材料丰富，节约资源且生产周期短，在各行业领域都有着巨大的应用前景[2-3]，然而激光烧结是一种复杂的热物理化学过程，受多种因素影响，成型件精度往往难以得到有效的控制，成为限制该技术在工业上普遍应用和进一步实际发展的重要原因，因此提高选择性激光烧结(selective laser sintering, SLS)成型件精度具有重要意义[4-5]。

目前，实际生产多采用试测法制定不同工艺参数组合[6]，然后根据成型效果寻找最优参数组合指导加工，这种方法往往需要花费大量的时间和成本，而且很难获得理想的关系模型[7]。随着机器学习和人工智能等科学的不断发展，为进一步提高激光烧结成型精度，越来越多的中外学者也尝试采用各种优化算法来建立工艺参数和尺寸精度间的映射关系。刘硕等[8]针对解决激光烧结增材制造过程中出现的几何尺寸误差问题，依据广义回归神经网络，建立了SLS工艺参数与收缩率间的定量模型，为实际加工中优化控制收缩提供参考；王丹妮等[9]应用粒子群算法和BP(back propagation)神经网络2种算法建立工艺参数与烧结件质量间的预测模型，同时分析了各因素间的相互关联，以此来选择相应加工参数；胡华清等[10]在大量实验基础上，利用遗传算法优化支持向量机确定了一定参数范围下的工艺参数组合方案，定性分析了各参数对于制件精度的本质影响；Sharma[11]提出利用人工神经网络建立扫描速度、扫描间距、预热温度与烧结精度之间的定量模型。

尽管上述算法在具体应用中均取得一定的效果，但由于算法本身存在收敛速度慢、搜索能力差。易陷入局部最优等缺陷，所以预测效果仍不尽人意。人群搜索算法是由Dai等[12]提出的一种新型元启发式算法，研究表明:人群搜索算法(seeker optimizaiton algorithm, SOA)相较于传统群智能优化算法具有更快的收敛速度和寻优精度[13]。结合SLS的工艺特点，选取激光功率、预热温度、扫描速度、扫描间距以及分层厚度五个工艺参数设计正交试验，提出了一种利用SOA算法优化BP神经网络初始权值和阈值的策略，对SLS成型件精度和工艺参数模型进行预测分析。最后将预测结果同PSO-BP以及传统BP神经网络预测结果进行对比，表明该方法具有良好的预测精度和更高的稳定性，可为实际生产提供科学指导。

1 SLS工艺参数的确定与实验

1.1 工艺参数的选取

SLS加工工艺参数与成型件间的精度具有非常复杂的非线性关系，影响成型结果的工艺参数主要包括激光功率、预热温度、扫描速度、扫描间距和分层厚度[14]。

1.1.1 激光功率

激光功率决定着单位时间粉末吸收的能量，激光能量密度是熔化粉末材料的主要能量输入来源，较高的激光能量会引起材料粉末瞬间熔化深度大于分层厚度，形成材料“过烧”[15]；反之，过低的激光能量会使粉末不能充分熔化，单层粉末难以粘结在一起。

1.1.2 预热温度

在正式加工前，材料粉末都要提前预热，预热能减少能量的消耗，缩短加工时间。若没有预热，将会使得零件成型时间增加，甚至无法烧结；当预热温度低于理想温度，零件因温差过大可能会出现严重的翘曲变形或错层现象；当预热温度过高，粉末会被直接烧结成型，不利于后期处理。

1.1.3 扫描速度

扫描速度即激光束扫描制件截面内部的速度，随着扫描速度的增大，材料难以充分熔融，反之随着扫描速度变慢，激光束产生的能量能熔化粉层内大部分粉末，制件致密度变高。

1.1.4 扫描间距

扫描间距决定了加工过程中热量分布状态以及相邻区域内材料的熔化程度。扫描间距小，则热应力大，从而使烧结效率变低；间距过大，则分辨率变低，成型精度低。

1.1.5 分层厚度

分层厚度即模型切片处理时的切片厚度，通常也被设置为铺粉厚度。分层厚度过小，扫描时间越长，效率越低，增加材料损耗，若分层厚度过大，则会产生“台阶现象”[16]。

1.2 实验样本数据的获取

实验设备为自主设计研发的CX-B200小型工业级激光烧结成型机，其主要技术参数如下:激光功率40 W，成型尺寸200 mm×200 mm×200 mm，分层厚度0.08～0.4 mm，最大扫描速度为2 000 mm/s，输入文件格式为Gcode。

本文中设计并采用直径25 mm、高度10 mm的圆柱体制件作为实验样件，实验材料为竹粉/共聚酰胺复合粉末[17]，同时选取激光功率P、预热温度T、扫描速度V、扫描间距L和分层厚度D作为正交试验的因子，设计了L16正交表，根据前期研究选取激光功率为10～25 W，预热温度为75～90 °C，扫描速度为1.0～2.5 m/s，扫描间距为0.10～0.25 mm，分层厚度为0.10～0.25 mm，每个因子的具体水平如表1所示。

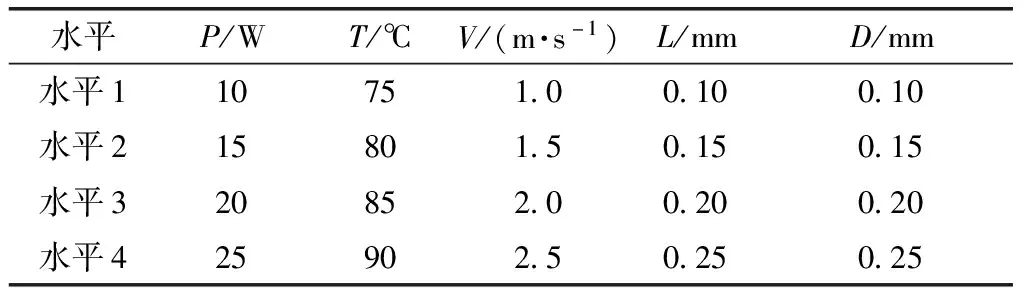
表1 正交试验因素水平

为了保证实验的准确性，本文中每组实验设计5个样件，分别采用游标卡尺和圆柱度测量仪测量5个样本的圆柱度误差Δε和高度误差ΔH并求取平均值作为每组实验结果，实验现场如图1所示。按正交表进行了16组实验，最终的实验样本数据如表2所示。

图1 实验样件模型

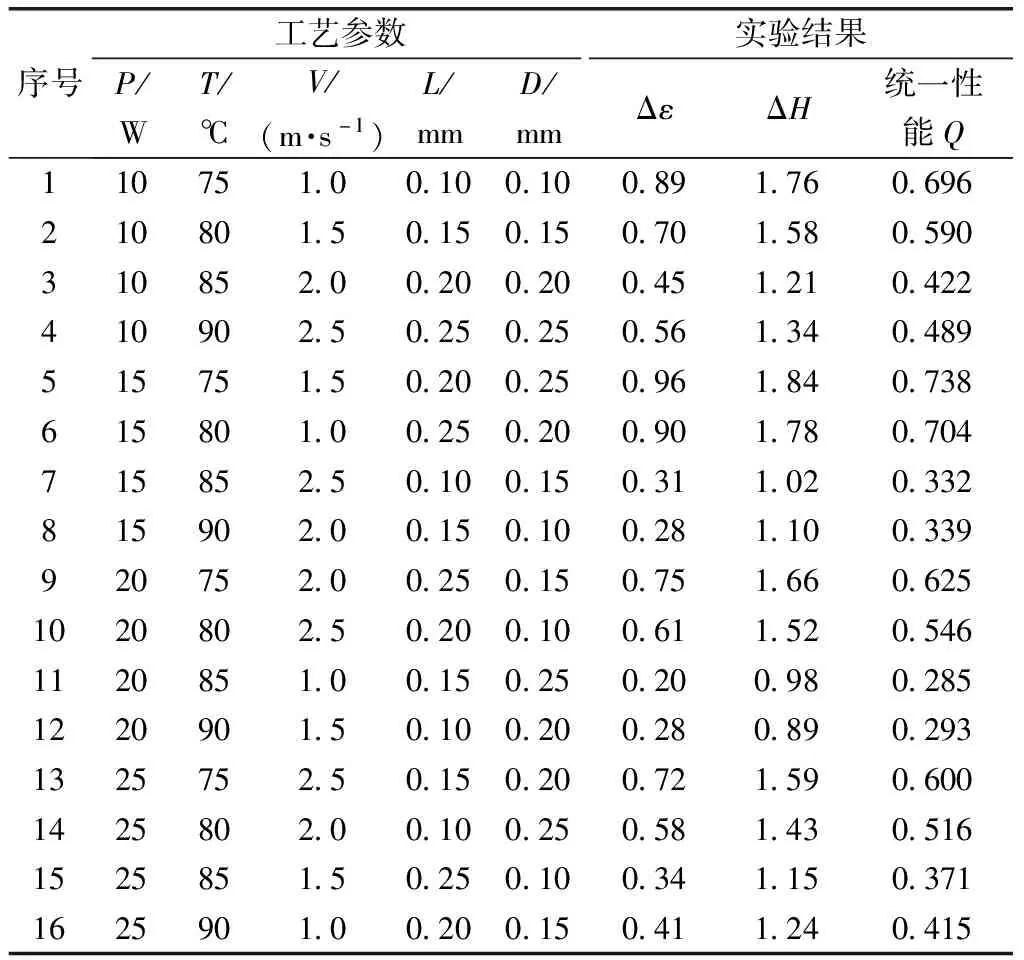
表2 实验样本数据

1.3 成型精度评价指标的确定

SLS工艺参数组合的选取是一个多目标优化问题。在多目标优化技术中，一般很难使其分目标同时达到最优[18]，本文利用线性加权组合法将其转化为统一目标函数，消除量纲并确定各项加权因子。

假设已知各项目标函数值的区间范围为

mj≤Yi≤nj，j=1,2,3,…

(1)

则

(2)

式(2)中：ΔYj为各目标函数容限，将加权因子取为

(3)

针对激光烧结工艺参数的优化问题，将实验样本数据中的圆柱度误差Δε和高度误差ΔH作为各项目标函数进行转化，得到成型件统一性能Q的目标函数为

Q=0.347Δε+0.220ΔH

(4)

式(4)中：转化后的统一性能Q作为成型件尺寸精度的评价指标，其函数值越小则成型精度越高。将上文实验数据代入式(4)中可以计算出目标函数值，见表2。

2 SOA-BP神经网络预测模型的构建

2.1 人群搜索算法

人群搜索算法是一种基于种群的新型启发式随机搜索算法，在该算法中，通过评估对应位置变化的响应，根据经验梯度来选择搜索方向，并基于模糊规则的不确定性推理来决定步长[19-20]。人群搜索算法具有概念明确、易于理解、收敛速度快和精度高等特点，其计算步骤如下。

2.1.1 搜索步长的确定

SOA算法在确定步长时先将个体最佳适度值按递减的顺序排列，并将个体赋予从1到N的顺序编号作为模糊推理的输入，采用高斯隶属函数表示搜索步长的模糊变量，即

(5)

式(5)中：uA为高斯隶属度；x为输入变量；u、δ均为隶属函数参数。

其他位置隶属度可表示为

(6)

uij=rand(ui,1)

(7)

式中：ui为第i个个体对应的隶属度；I(i)表示第i个个体最佳适应度值按降序排列后的顺序编号；N为种群规模；Umax为最大隶属度，Umin为最小隶属度；uij为j维搜索空间的目标函数值i对应的隶属度；函数rand(ui,1)产生均匀随机分布在[ui,1]上的实数。

搜索步长公式为

(8)

式(8)中：aij为j维搜索空间的搜索步长；δij为高斯隶属函数的参数，计算公式为

δij=ω(t)|zbest-10rand(1,3)|

(9)

(10)

式中：zbest表示全局最优；rand(1,3)表示产生均匀随机分布在[1,3]上的实数；ω(t)为第t次迭代的权重函数值，随迭代次数的增加从0.9线性递减至0.1，t为当前迭代次数；MaxIter为最大迭代次数。

2.1.2 搜索方向的确定

在确定搜索步长后，通过将第i个个体与个体最佳和全局最佳进行比较确定搜索方向是利己方向di,ego、利他方向di,alt还是预动方向di,pro，表示为

di,ego(t)=gi,best-xi(t)

(11)

di,alt(t)=zi,best-xi(t)

(12)

di,pro(t)=xi(t1)-xi(t2)

(13)

式中：gi,best表示第i个搜寻个体所在领域的群体历史最优位置；zi,best表示第i个搜寻个体寻经过的最优位置；xi(t)为个体当前位置。

通过采用三个方向的随机加权几何平均数为标准确定搜索方向，计算公式为

di(t)=sign(ωdi,pro+φ1di,ego+φ2di,alt)

(14)

(15)

式中：ω为惯性权值；φ1和φ2为常数，它们的取值范围为[0,1]内均匀分布的常数；t为当前迭代次数，取值为[2,MaxIter]之间的整数，权重最大值ωmax，权重最小值ωmin。

2.1.3 个体位置的更新

确定搜索步长和方向后，要对个体位置进行更新，位置更新公式为

Δxij(t+1)=αij(t)dij(t)

(16)

xij(t+1)=Δxij(t+1)+xij(t)

(17)

2.2 SOA算法优化的BP神经网络模型

BP神经网络(back propagation neural network，BPNN)是一种采用误差反传算法的多层前馈网络[21]，标准的BP神经网络模型主要由输入层、隐含层和输出层组成，其网络拓扑结构如图2所示。

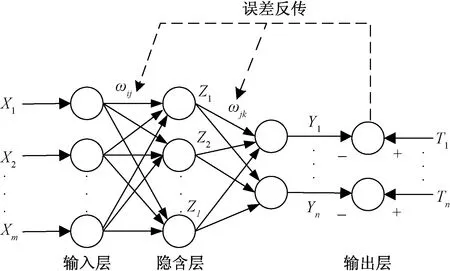
X1, X2,…, Xm表示m个实际输入；ωij表示输入层和与隐含层之间的连接权值；Z1,Z2,…,Zl表示l个隐含层；ωjk表示隐含层和输出层之间的连接权值；Y1, Y2,…, Yn表示n个预测输出；T1, T2,…, Tn表示n个期望输出

神经网络隐含层的节点个数计算公式为

(18)

式(18)中：m为输入层节点数；l为隐含层节点数；n为输出层节点数；a0为0～10的常数。

隐含层和输出层输出分别为

(19)

(20)

式中：f(·)为激励函数；aj为初始隐含层阈值；bk为输出层阈值。

尽管传统BP神经网络具有良好的逼近非线性映射能力，但其随机生成的初始权值和阈值难以准确获得，在迭代后期容易陷入局部最优点从而导致预测结果差别较大，预测效果不稳定。为弥补BP神经网络的局限性，通过人群搜索算法优化BP神经网络，用优化后的最优解作为BP神经网络迭代的权值和阈值，提高预测模型的效率和准确性。SOA算法优化BP神经网络的主要步骤如下。

步骤1预处理样本数据，确定BP神经网络结构并初始化BP神经网络各层连接权值和阈值。

步骤2初始化人群搜索算法的种群规模、种群个体、迭代次数、最大最小隶属度以及权值的最大值和最小值。

步骤3用训练后的BP神经网络得到的预测值与真实值之间的误差作为适应度值，将样本数据代入适应度函数中，计算全局最优、个体最优、个体最佳适应度和全局最佳适应度。

步骤4初始化经验梯度方向，确定搜索步长、搜索方向，确定搜索策略，将计算得到的步长和方向进行位置更新，更新个体和全局最优和最佳适应度值，直到迭代满足终止条件，输出。

步骤5将最佳网络权值和阈值赋值BP神经网络初始权值和阈值。

步骤6BP神经网络训练，初始化网络参数，调用Levenberg-Marquardt函数为训练函数，经过训练，将样本数据输入该模型进行预测，得到预测精度值，分析结果。

基于SOA-BP神经网络的选择性激光烧结成型件精度预测算法流程如图3所示。

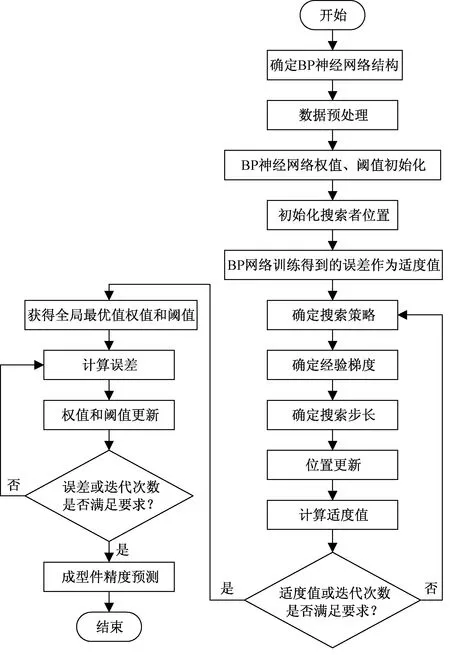
图3 SOA优化BP神经网络算法流程图

为加快梯度下降求最优解的速度，提高预测模型精度，在预处理样本数据时，还要对数据进行归一化处理[22]；在预测输出时，为了方便观察，对归一化的数据进行反归一化即可。采用Min-Max方法将样本数据归一化为[0,1]区间的小数，归一化公式为

(21)

式(21)中：x′为归一化后的样本数据值；xi为第i个样本数据；xmin为样本数据的最小值；xmax为样本数据的最大值。

3 基于SOA-BP神经网络模型的预测实验与分析

本文的BP神经网络输入为:激光功率、预热温度、扫描速度、扫描间距、分层厚度五个工艺参数，故输入层节点个数为5，网络输出选择统一性能Q，故输出节点个数为1；隐含层节点个数根据式(18)计算得出为9，因此整个BP神经网络结构为5-9-1；初始化SOA算法最大隶属度Umax=0.95，最小隶属度Umin=0.011 1，权重最大值ωmax=0.9，权重最小值ωmin=0.1，种群规模N=30，最大迭代次数MaxIter=500，选用Levenberg-Marquardt函数训练BP神经网络，设定学习目标误差为1×10-6。为了更好地展示结果，下面给出在相同实验条件下基于SOA优化、PSO优化的BP神经网络和传统BP神经网络对16组统一性能Q的预测结果，如图4和表3所示。

结合图4和表3可以看出，SOA-BP神经网络的预测值和真实值之间的误差相对传统BP神经网络和PSO-BP神经网络要小，与真实值的折线图更接近，更吻合。优化前的BP神经网络最大绝对误差为0.123，最小绝对误差为0.030；PSO优化后的BP神经网络最大绝对误差为0.055，最小绝对误差为0.008；SOA优化后的神经网络最大绝对误差为0.028，最小绝对误差为0.003，整体上看SOA-BP神经网络预测结果与真实值更加接近，这说明基于SOA-BP算法进行选择性激光烧结成型件精度预测的准确性更高。

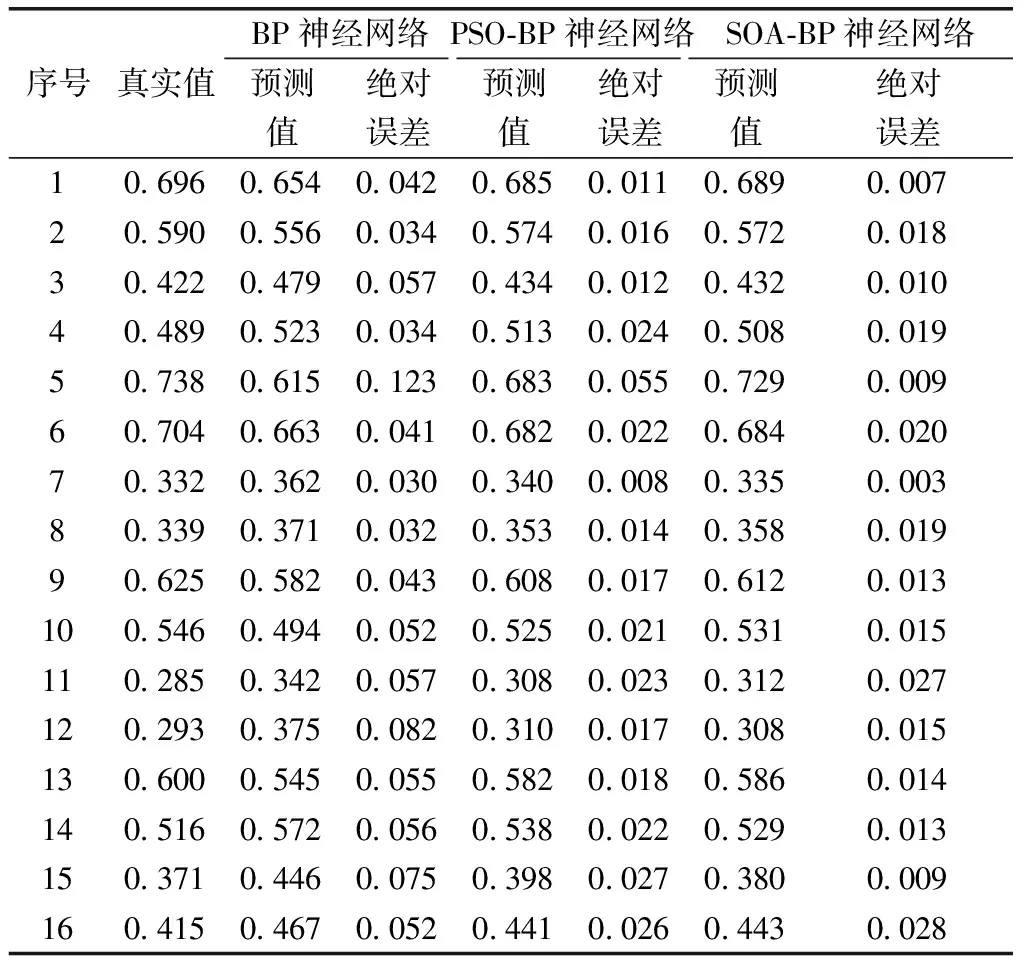
表3 预测结果对比

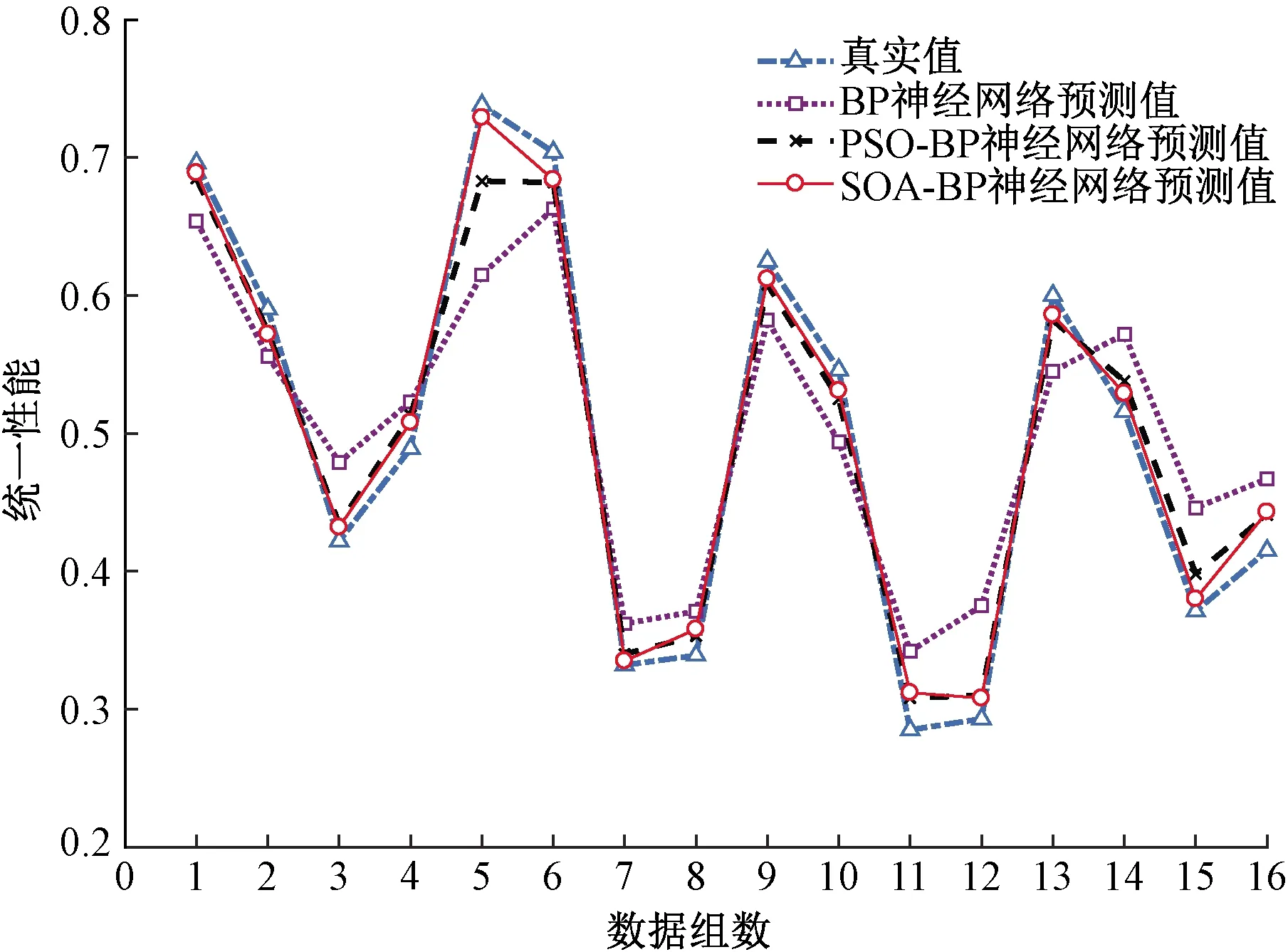
图4 不同预测算法的预测结果

为更直观地评估本文构建的精度预测模型的精确性和优越性，选择均方根误差(root mean square error, RMSE)、平均绝对百分比误差(mean absolute percentage error, MAPE)和平均绝对误差(mean absolute error, MAE)这三种误差指标来衡量预测值与真实值的差异。

均方根误差指标为

(22)

平均绝对百分比误差指标为

(23)

平均绝对误差为

(24)

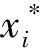
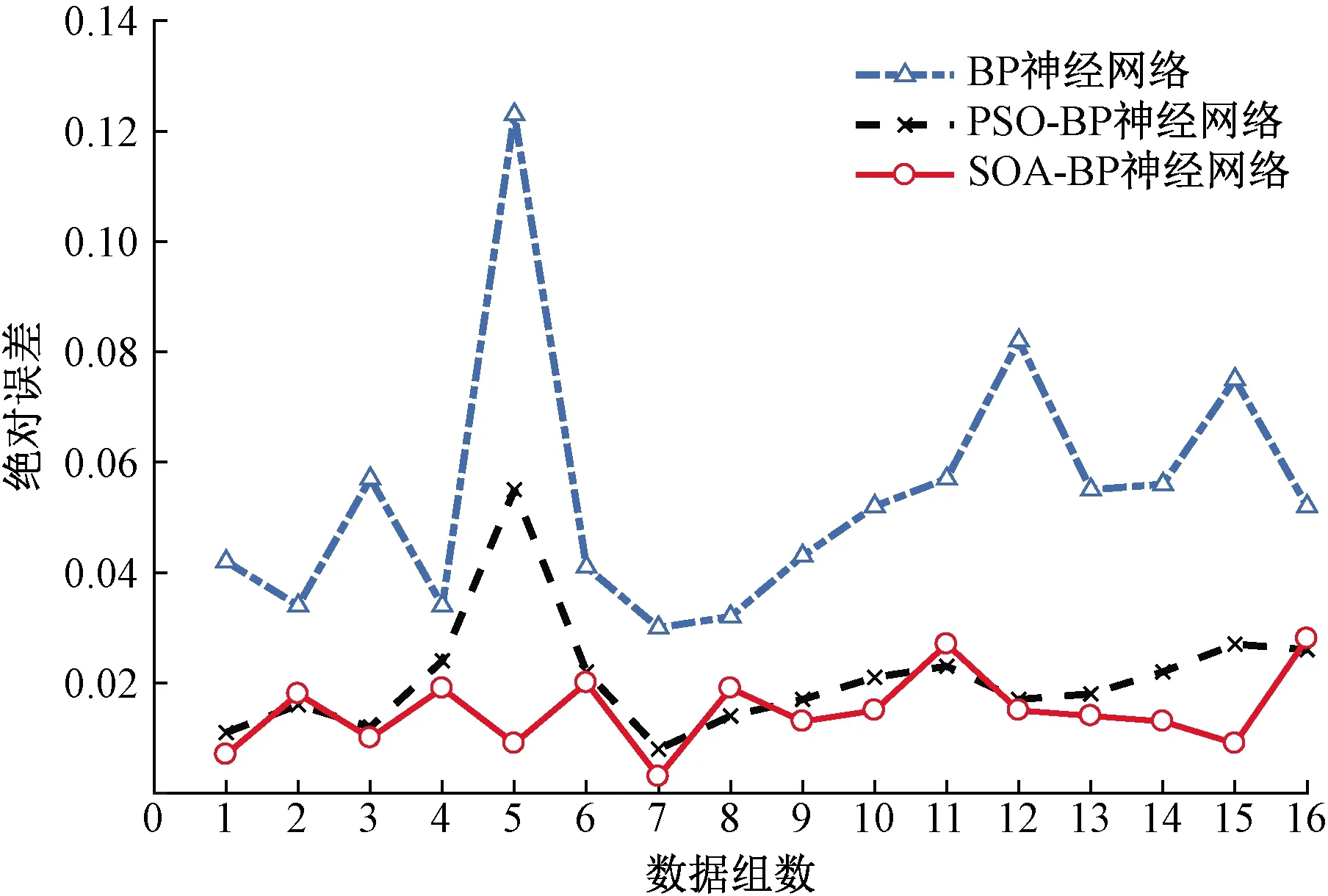
图5 不同预测算法绝对误差对比

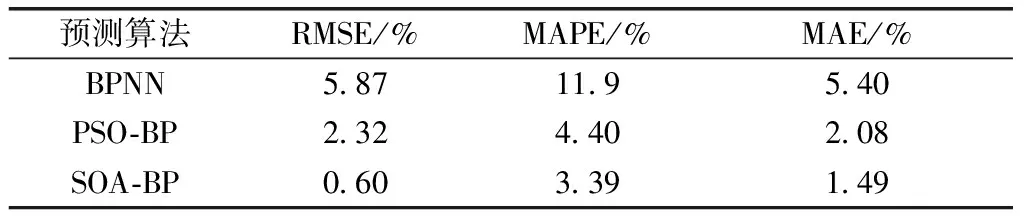
表4 精度对照表

从表4可以宏观地看出，基于SOA-BP神经网络得到的预测值与真实值之间的均方根误差、平均绝对百分比误差、平均绝对误差相比于传统BP神经网络分别减少了5.27%、8.51%、3.91%，相比PSO算法优化后的BP神经网络分别减少了1.72%、1.01%、3.91%，分析得出SOA-BP神经网络预测算法可以有效预测激光烧结成型件精度，且相较于其他两种算法具有更高的准确性。

4 结论

提出了一种基于SOA-BP神经网络的SLS成型件精度方法，得到以下结论。

(1)选取激光功率、预热温度、扫描速度、扫描间距以及分层厚度五个工艺参数设计正交试验获取样本数据，建立了激光烧结成型的工艺参数与其成型件精度之间的映射关系，解决了难以用数学方法建立精确模型的问题。

(2)对比PSO-BP神经网络、传统BP神经网络的预测结果，SOA-BP神经网络具有更高的预测精度。

(3)SOA-BP神经网络得到的预测值与真实值之间的均方根误差、平均绝对百分比误差、平均绝对误差分别为0.60%、3.39%、1.49%，这一结果对于绝大多数预测模型来说是可以接受的，为提高SLS成型件精度具有实际的参考价值。