移动荷载作用下离散支承曲线轨道振动特性分析

郑晨晨 ,黄 强 ,刘干斌

（1.宁波大学 岩土工程研究所,浙江 宁波 315211;2.宁波大学 滨海城市轨道交通协同创新中心,浙江 宁波 315211）

由于地形、地质条件和地下建筑物等原因,轨道交通线路往往需要设置大量的曲线线路,小半径的曲线地铁线路也在逐渐增多[1-3].列车在曲线轨道上运行产生的振动响应问题较之直线轨道更为严重.直线轨道只承受车辆的竖向荷载,而曲线轨道内外轨高差使得钢轨需要承受横向荷载,且受速度影响明显.如横向振动产生轨道波磨问题会对轨道和列车车轮产生很大影响,关系到列车的行车安全[4].曲线轨道的振源频率更广、振动幅值更大、横向加速度响应更为明显.根据实测数据[5],地铁列车通过曲线轨道时地表50 m 范围内的水平向振动加速度有效值可达竖向的2～4 倍.随着城市曲线线路增多,曲线轨道的振动问题逐渐受到关注[6-8].

国内外很多学者对曲线轨道的振动问题进行了研究.Dai 等[9]采用三角级数法对单层连续支承曲线梁的振动响应进行了研究,分析了扣件阻尼、曲线半径、移动速度等因素对曲线梁各向位移的影响,但没有考虑轨道离散支承的影响.刘维宁等[10]将曲线轨道简化为周期性离散支承曲线梁,首次推导出离散支承下曲线Timoshenko 梁平面外振动响应的解析解,发现曲线梁振动响应与荷载速度密切相关,但没有对平面内的振动响应进行进一步分析.王开云等[11]采用Ritz 法得到了离散支承型Euler 梁的扭转振动方程,研究了直线梁的振动响应,但忽略了曲率对梁扭转振动的影响.杜林林等[12-13]利用周期性结构原理,将曲线轨道视为离散支承结构,在频域下分析了曲线梁扭转振动响应;并用基于模态叠加法分析了移动简谐荷载下曲线轨道的空间振动特性,得到了频域下曲线梁的响应解答,但其曲线轨道位移的频域解答过程较复杂繁琐,一般用来分析轨道位移的频谱响应特征.时域解答更为直观,可以直接得到轨道位移随列车移动时的振动响应,当移动荷载为简谐荷载时,也可分析轨道频率特性.总的来看,目前时域解答多针对连续支承曲线轨道的情况,较少反映离散支承的影响.地铁轨道是由一个个离散的扣件支承而成,因此离散支承的影响不可忽视.

本文采用时域分析方法对离散支承曲线轨道的振动特性进行分析,揭示曲线轨道时域下的空间振动特性.以地铁隧道内的整体式曲线轨道为例,首先基于振型叠加法推导出离散支承下曲线轨道的空间振动常微分方程,然后利用Runger-Kutta 法,采用Matlab 软件编程求解该方程,分析移动荷载下离散支承曲梁平面内外的振动特性,最后对比不同工况下的轨道位移响应,以期为曲线轨道的减振提供参考.

1 曲线轨道振动响应求解

1.1 曲线梁振动方程

考虑到隧道质量和刚度远大于钢轨,隧道可视为固定端,将整体式曲线轨道简化为单层离散支承的Euler 长梁.假定曲线梁为等截面均质梁,曲率半径为常数且远大于梁截面尺寸,按照右手螺旋法建立坐标系(图1).钢轨受力计算模型如图2 所示,其振动方程如式(1).

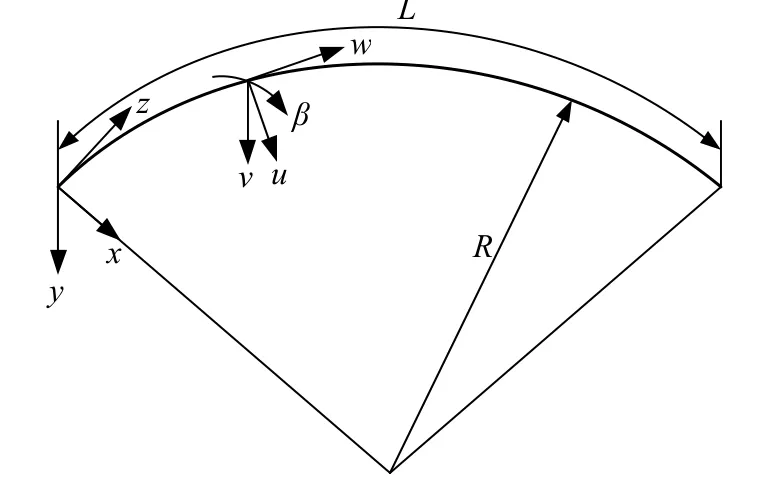
图1 整体式轨道位移示意图

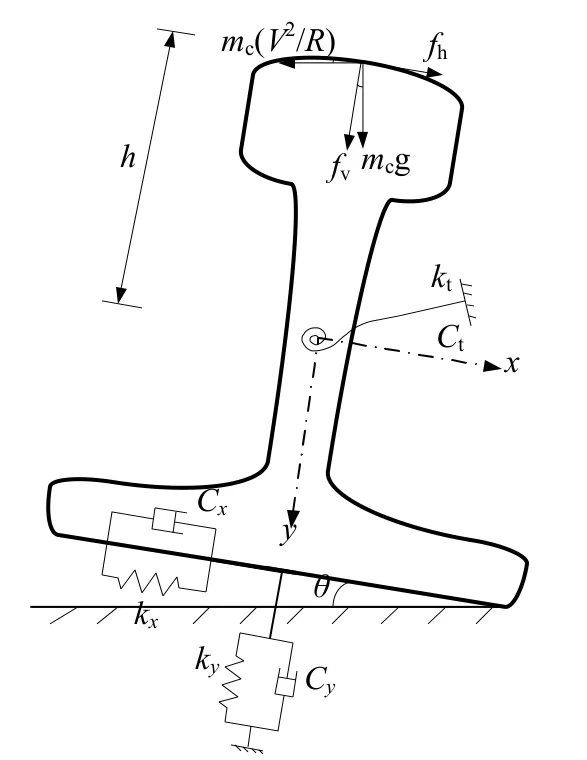
图2 钢轨截面受力图

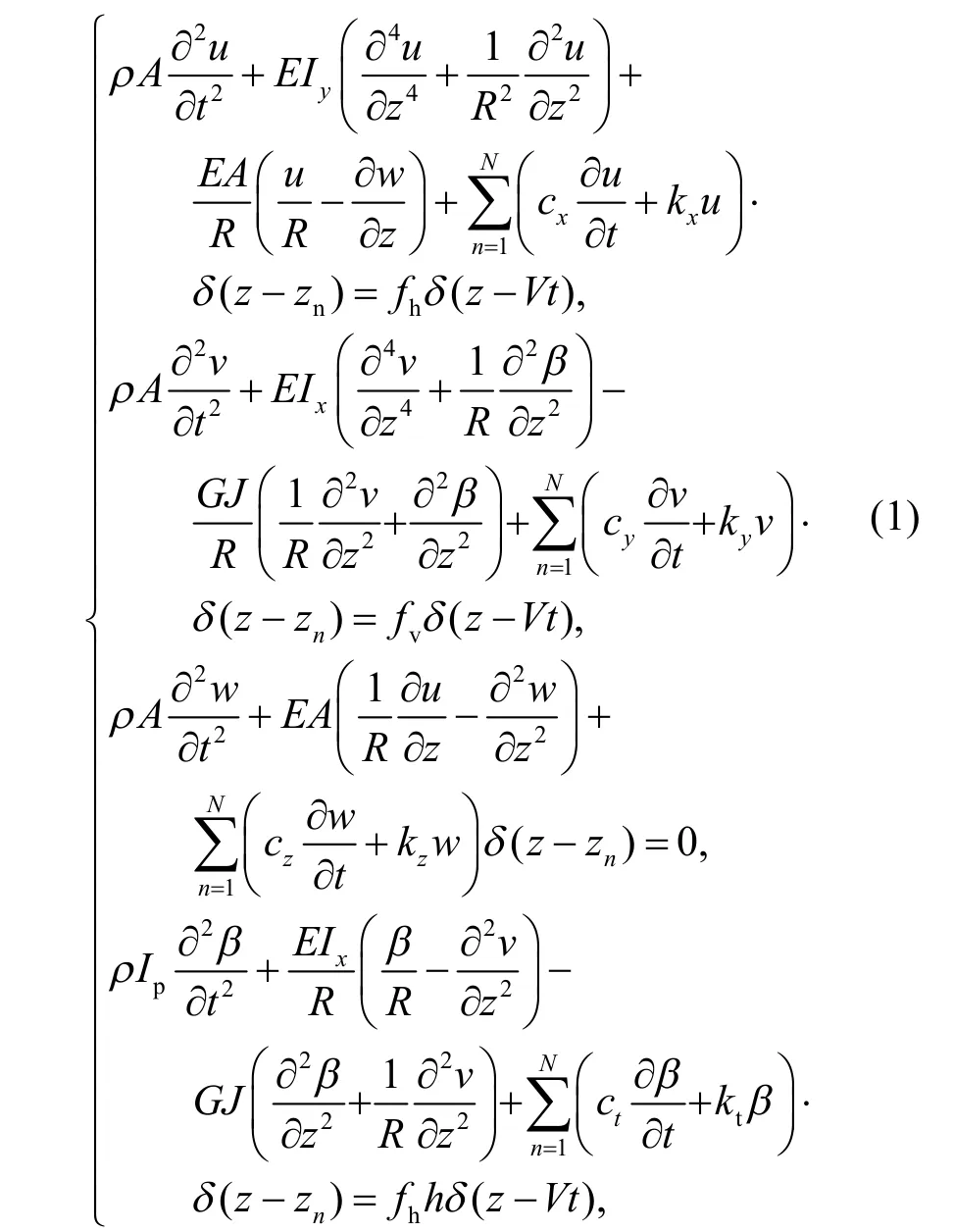
式中:ρ和A为曲线梁的密度和截面积;u为x方向位移(径向位移);v为y方向位移(竖向位移);w为z方向位移(轴向位移);β为扭转变形;Ix为绕x轴的惯性矩;Iy为绕y轴的惯性矩;Ip为截面极惯性矩;J为扭转常数;E和G分别为曲线梁的弹性模量和剪切模量;kx和cx、ky和cy、kz和cz分别为x、y、z方向的弹簧刚度和阻尼系数;fv和fh分别为作用在曲梁顶端的竖向和径向荷载;h为梁顶部与中性轴之间的距离;R为曲线梁的半径;zn为第n个扣件位置,等于 (n-1)dc;dc为扣件间距;列车速度为V.

1.2 振动方程求解

利用振型叠加法求解方程(1),根据Euler 梁理论,其振型函数可采用简支梁正则振型函数,其表达式为:

式中:Yi(z)为正则振型函数;qi(t)为对应的时间坐标函数;nm为振型数目.

对于Euler 长梁,其振型函数可表示为[14]:

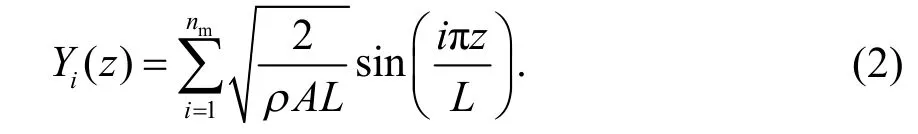
将正则振型函数代入式(1),经过傅里叶变换并简化,可将偏微分方程变换为如下常微分方程:

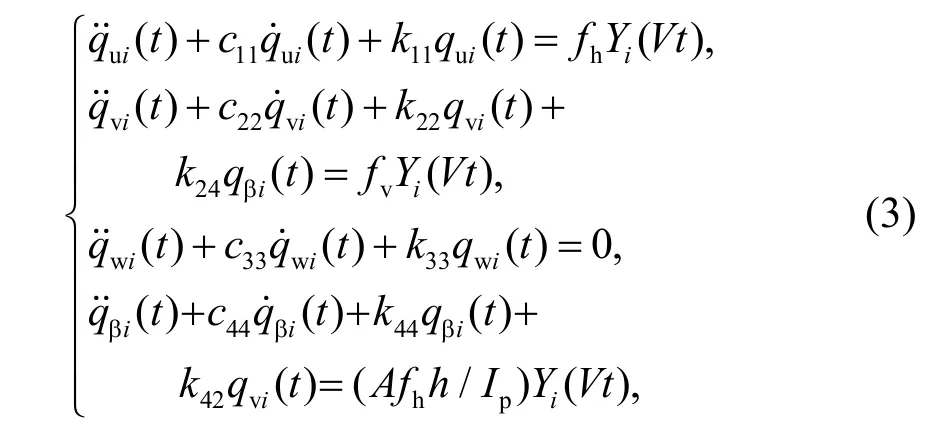
式(3)各系数为:

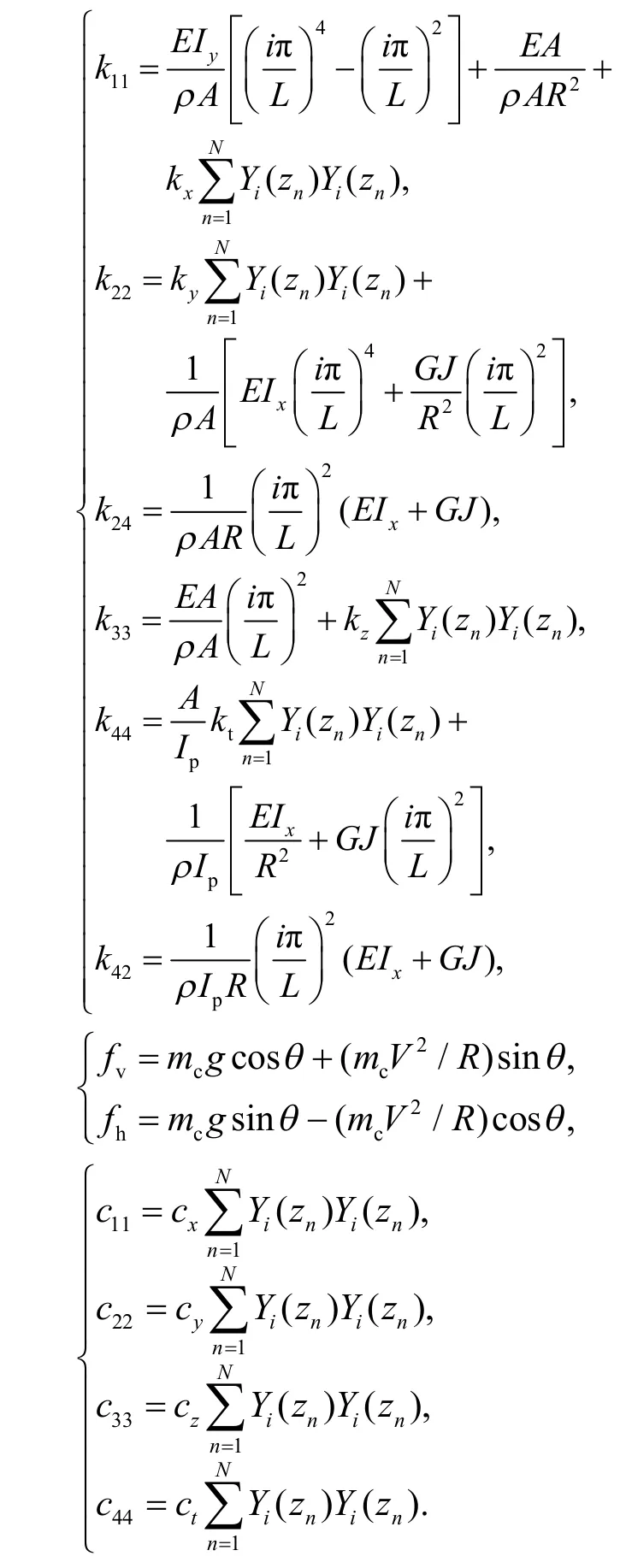
对方程组(3),可写成如下矩阵形式:

1.3 计算结果验证

经计算振型数目取120 能满足计算精度要求(图3).为验证本文所采用计算方法的准确性,参照文献[13]模型参数(表1),将本文计算结果与文献[13]结果进行对比.

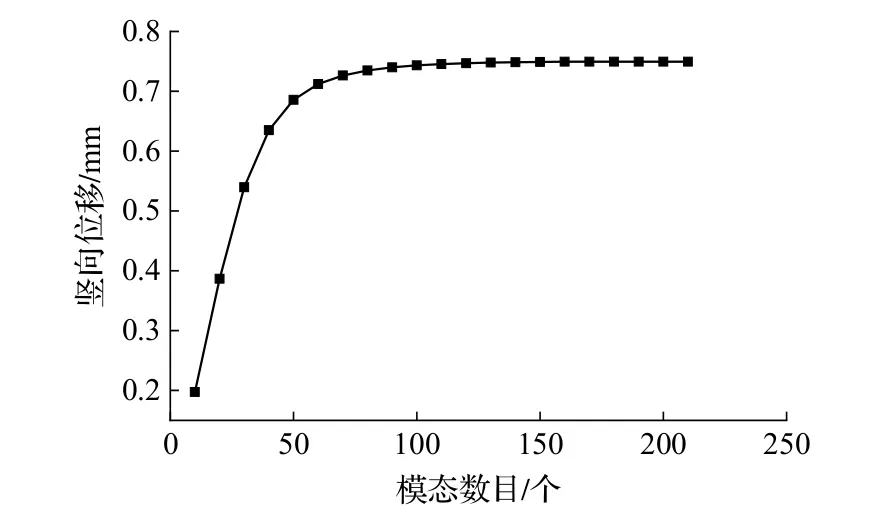
图3 竖向位移幅值随模态数目的变化

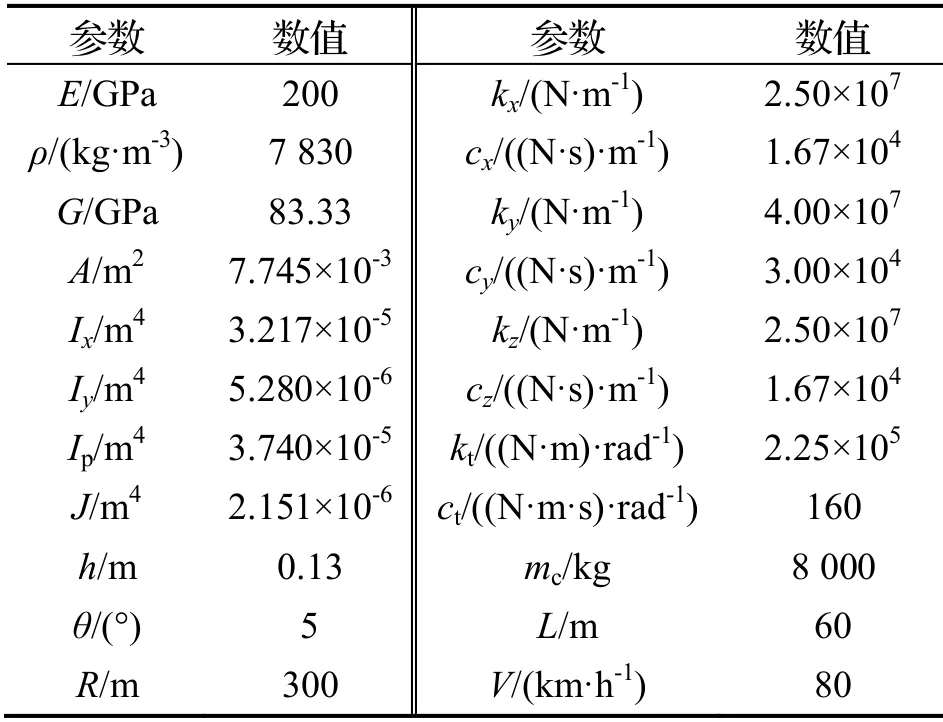
表1 T60 钢轨及DTVI2扣件参数[13]

图 4 为本文计算方法与文献[13]的对比结果.从图4 可知,两者径向位移、竖向位移和扭转变形响应结果基本一致,表明本文计算方法准确、可行.

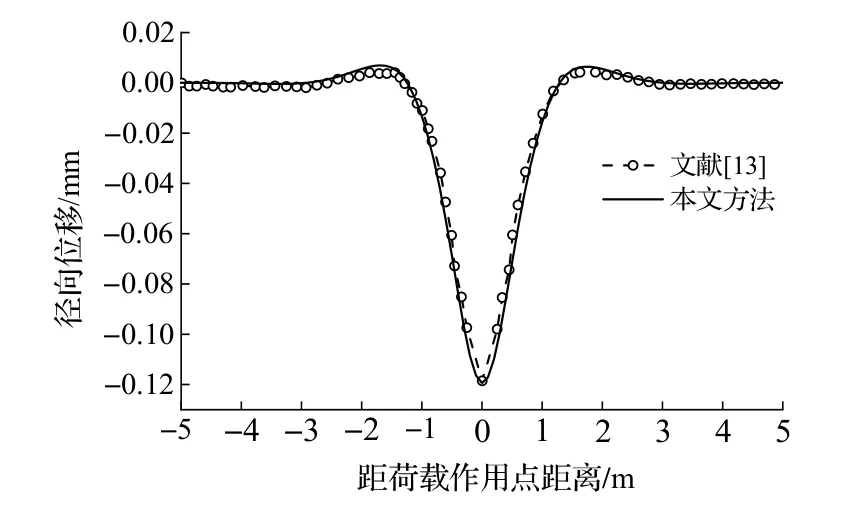
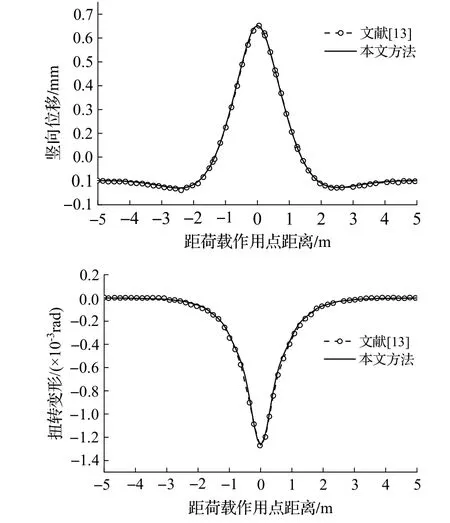
图4 曲线梁径向、竖向位移与扭转变形对比

2 曲线轨道振动特性分析

基于上述轨道参数,对曲线轨道的时域振动特性进行分析,研究扣件、曲率半径、超高角以及荷载列车速度对曲线轨道动力响应的影响.结果发现,径向位移与扭转变形的变化规律相似(都与fh的变化有关).因此,仅分析竖向挠度、径向挠度的响应规律.选取曲线轨道中点(支点处)的位移响应进行分析.

2.1 扣件影响

在我国轨道交通系统中,扣件间距大部分采用600～650 mm,而国外则相对较大,如新加坡整体式道床扣件间距为700 mm.相比之下,我国采用的扣件间距比较保守,在一定程度上提高了成本,增加了后期维护的费用.扣件对于钢轨有两大影响因素:扣件间距和支承刚度.选取曲线半径300 m 下10～40 MN·m-1的支承刚度,600～700 mm扣件间距进行分析,结果如图5 和图6 所示.

从图5 和图6 可知,钢轨的位移变化量随着支承刚度的增加而减小,随着扣件间距的增大而增大.当扣件间距为600 mm、支承刚度为40 MN·m-1时,竖向位移有最小值0.75 mm;当扣件间距为700 mm、支承刚度为10 MN·m-1时,竖向位移有最大值2.38 mm.在荷载作用下,钢轨位移受扣件支承刚度影响较大,受扣件间距影响较小.以钢轨间距650 mm 为例,径向支承刚度从6.25 MN·m-1增加到25 MN·m-1时,径向位移减小了66.8%,竖向支承刚度从10 MN·m-1增加到40 MN·m-1时,竖向位移减小了64.8%;在竖向支承刚度为40 MN·m-1时,扣件间距从700 mm减小到600 mm时,竖向位移仅从0.84 mm 减小到0.75 mm,变化量很小.因此,在移动荷载作用下减小扣件间距对减小钢轨位移的影响并不明显,增加扣件支承刚度则能有效减小钢轨产生的位移.

图5 不同支承刚度下径向位移随扣件间距的变化

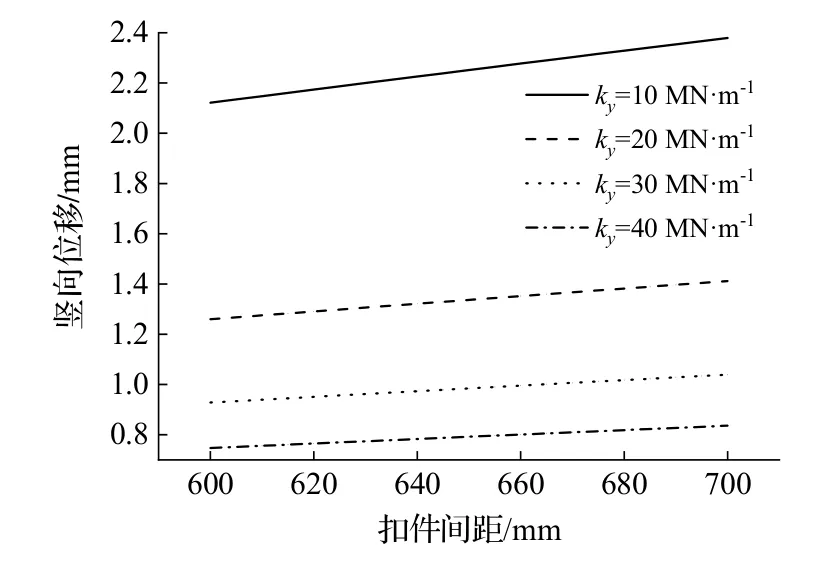
图6 不同支承刚度下竖向位移随扣件间距的变化

2.2 半径影响

由于横向曲率的存在,曲线轨道的振动较直线轨道更为复杂,曲线半径是关键因素.以列车速度20 m·s-1为例,半径300～1 500 m,轨道超高角为5º,超高为120 mm,满足规范里对超高上限的要求[15].

图 7 为不同曲线半径时径向位移峰值的变化曲线.从图7 可知,随着半径增加,径向位移方向发生改变,从负值变为正值,当曲线轨道半径增加至500 m 时,径向位移为零.直梁因没有承受横向力,所以径向位移始终为零.这表明列车速度和超高角一定时,可以选择合适的曲线半径使得径向位移为零.

图7 不同曲线半径时径向位移峰值的变化

图 8 为不同曲线半径时竖向位移峰值的变化.从图8 可看出,在列车运行速度范围内,竖向位移基本不随半径增加而发生变化,且与直梁相差极小,其主要原因是竖向振动荷载随曲线半径的变化不明显.可见,当列车设计速度和设计超高角确定后,可以确定最佳的曲线半径,使得径向的振动位移最小.

图8 不同曲线半径时竖向位移峰值的变化

2.3 超高角影响

曲线轨道正是由于超高角的存在,使得部分惯性力与重力分力平衡.因此,从横向荷载传递来看,超高角能减小钢轨所受的横向荷载.不同曲率半径下径向位移和竖向位移随超高角的变化如图9和图10 所示.为更加直观地看出规律,将图9 数据进行绝对值处理.

从图9 和图10 可知,曲线轨道超高角对径向位移的影响比竖向位移更明显.半径不变时,随着超高角的增加,径向位移幅值先减小后增大,在理想超高角(θ=arctan(V2(gR)-1))时径向位移为零.例如,轨道半径为600 m,列车运行速度为20 m·s-1时其理想状态超高角近似4º.随着轨道半径的增加,径向位移随超高角的变化规律趋于一致.

图9 不同曲线半径时径向位移随超高角的变化

图10 不同曲线半径时竖向位移随超高角的变化

当曲线半径较小时,竖向位移随着超高角的增加呈现先增加后减小的趋势;当曲线半径不断增大时,竖向位移随超高角的增加逐渐下降.这是由于fv与重力分力和惯性力分力有关,在小半径曲线下,惯性力分力增加量比重力分力减小量要多,因此竖向荷载增加,从而造成竖向位移增加.

2.4 速度影响

列车速度对曲线轨道振动响应有重要影响,鉴于三向位移变化规律相同,以径向位移为例,不同速度下径向位移时程的变化如图11 所示.

图11 不同速度时径向位移时程的变化

在目前列车速度下列车的振动荷载作用近似于准静态荷载作用,曲线轨道不会发生共振现象,最大位移出现在拾振点处.事实上,列车速度产生的影响还与轨道超高角和曲线半径有关,因此有必要综合分析,不同超高角和曲线半径下位移随速度的变化如图12～15 所示.

图12 不同超高角时径向位移随速度的变化

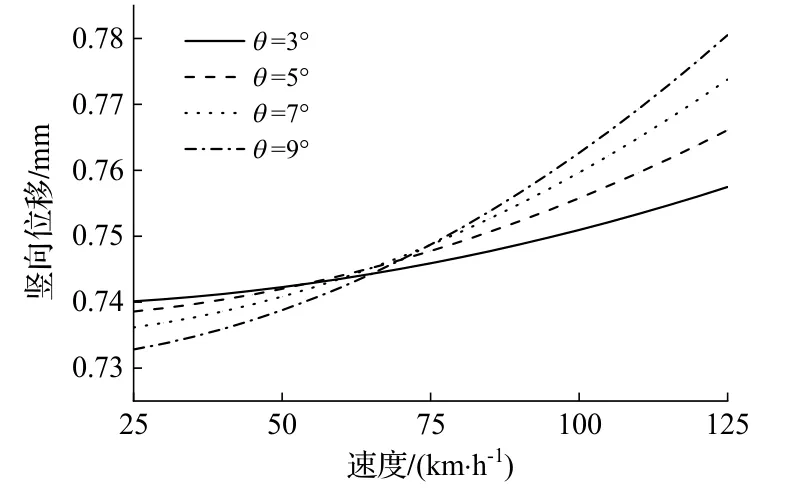
图13 不同超高角时竖向位移随速度的变化

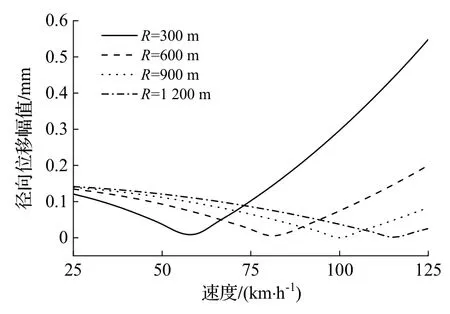
图14 不同曲线半径时径向位移随速度的变化

图15 不同曲线半径时竖向位移随速度的变化

由图12、13 可看出,超高角对曲线轨道径向位移、竖向位移影响较大,但超高角变化对径向位移和扭转变形的影响更大;超高角越小对应的理想车速也越小.荷载移动速度对曲线轨道径向位移影响更加明显,特别是当列车速度大于理想车速后,径向位移随速度的增加值远大于竖向位移.由图14、15 可发现,半径对曲线轨道径向位移和竖向位移有显著影响,随着半径的增加,各向位移变化曲线的斜率逐渐减小,在大半径曲线轨道中速度对曲线轨道动力响应的影响较低.可见,列车在小半径曲线轨道运行时要将速度控制在理想车速附近,以减小轨道产生更大的径向位移.

3 结论

(1)扣件的支承刚度是影响曲线轨道位移幅值的主要因素,减小扣件间距并不能有效减小钢轨产生的位移,增加扣件支承刚度对钢轨位移减小有明显作用.

(2)在目前的列车速度下,列车移动荷载近似于准静态荷载作用,钢轨不会发生共振,最大位移出现在拾振点处.

(3)曲线半径、超高角、列车速度三者之间相互影响,列车径向振动存在一个理想状态.随着半径的增加,横向荷载方向会发生转变,导致径向位移幅值先减小后增大.

(4)荷载移动速度对径向位移、扭转变形影响较大,竖向位移受速度影响较小,随着速度的增加,径向位移和扭转变形的振动响应先减小后增加,中间存在理想速度状态.