浅谈小学数学思想方法在计算教学中的应用

邱明清

《义务教育数学课程标准（2011版）》明确提出：把培养学生的“运算能力”作为数学核心素养。掌握算法、形成运算技能一直是传统计算教学的重点，但这并不是运算能力的全部。新课程背景下的计算教学不仅要求学生掌握正确的计算方法和熟练的计算技能，更重要的是为学生创造广阔的思维空间，让学生亲历算法的探索过程，在建构知识的过程中感悟基本数学思想、积累基本活动经验、发展数学思维能力。那么，在小学数学计算教学中，要让学生感悟哪些数学思想方法？如何去渗透这些数学思想方法？下面，笔者结合自己的教学案例浅谈在计算教学中如何让数学思想方法悄然绽放。

一、直观操作，让学生在演示中感受数形结合思想

数形结合思想就是通过数和形之间的对应关系和相互转化来解决问题的思想方法。它借助简单的图形、符号和文字所表示的示意图，使抽象的数学问题直观化，使繁难的数学问题简洁化，使原本需要通过抽象思维解决的问题，让学生在具体的操作活动中理解和掌握知识、解决问题。可见，直观操作就是“以形助数”，是数形结合思想很好的切入点。因此，在计算教学中，教师可以根据学生的认知特点设计实践活动，加强直观操作，帮助学生理解算理，让学生在理解算理的基础上掌握计算方法，感悟数学思想方法。

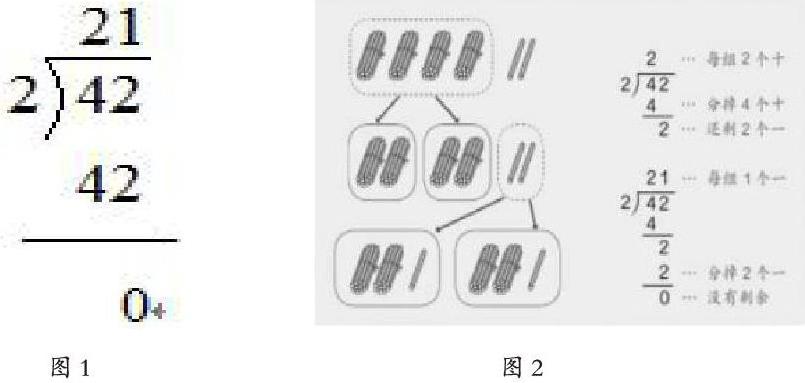
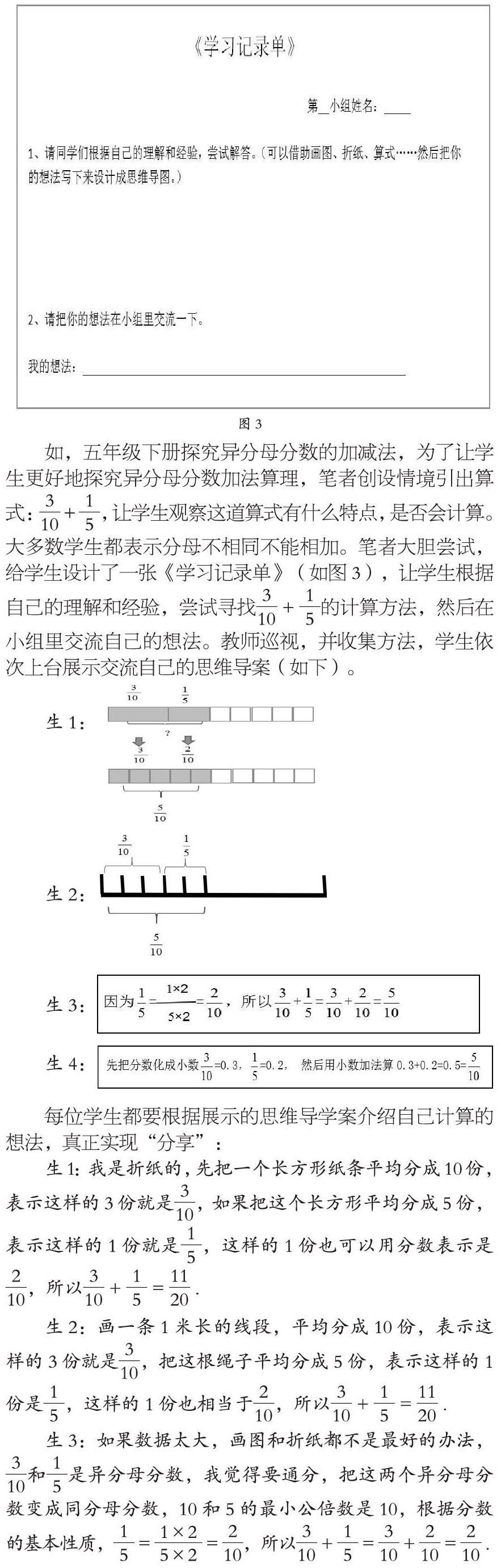
例如，在探究三年级下册“一位数除两位数的笔算除法”例1时，学生弄懂题意后，笔者让学生先口算出得数，并说出口算的过程，再要求学生用小棒来分一分，边分边说如何分。学生虽然会口算结果，但未能把分的过程和结果用竖式表示出来，大多数学生列出的竖式如图1。为了帮助学生理解42÷2笔算算理，笔者让学生摆一摆小棒，再结合摆的过程说一说“刚才分小棒分了几次？”“第一次分的是什么？第二次呢？能在小棒图中圈出来吗？在竖式中是怎样体现这两次分小棒的过程的？”“图中的小棒对应的是哪个数？”当学生汇报时，笔者利用课件直观演示小棒分的过程，对应着分步呈现竖式计算的过程，通过直观演示小棒图，让学生在数形结合中直观理解，使学生明确每一步计算结果的含义：原来竖式图2的写法是表示分小棒的过程，先分几个十，再分几个一，所以，写的时候先算十位 ，再算个位，把分的过程记录下来，就写出了除法竖式，建构了除法竖式的意义。

通过直观操作，教师给学生创设了实践操作平台，让学生将直观操作与竖式计算相对照，并通过摆一摆、想一想、说一说、看一看、写一写等形式，使学生充分体验由直观操作转化成抽象表述的过程，实现了从算理到算法的自然过渡。在这个过程，学生真真实实地感受到数形结合思想，也获得数学的基本活动经验，培养了学生的运算能力，同时促进了学生的思维能力发展。

二、思维碰撞，让学生在交流中感悟数学优化思想

计算允许多样化，但“多样”只有得到“优化”，才能更好地促进学生运算能力的提高。在计算的过程中，教师要让学生根据已有的知识经验，让他们在多样化的算法中找到一个普遍都能接受的、最能理解和最容易掌握的算法的过程，在这过程中感悟数学优化思想。

例如，四年级下册学生掌握了乘法结合律和乘法分配律后，为了让学生体验解题策略多样化，笔者让学生解决问题：“王老师购买25筒羽毛球，一筒12个，王老师一共买了多少个羽毛球？”要求学生自主探究计算方法，得出结果，然后在班里交流想法。

学生的板演情况展示如下：

生1：笔算12×25=300

生2：12×25=（3×4）×25=3×（4×25）=3×100=300

生3：12×25=（10+2）×25=10×25+2×25=250+50=300

生4：12×25=（2×6）×25=6×（2×25）=6×50=300

生5：12×25=（4+6+2）×25=4×25+6×25+2×25=100+150+50=300

生6：12×25=（3×4）×25=3×25+4×25=75+100=175……

看到學生出现这么多不同的计算方法，笔者马上追问：对以上同学的计算方法，你有什么意见？

生7：生6和生2都是把12拆成4×3，可计算结果不相同。

生8：他的计算结果都跟其他人不相同，肯定是错的？

师：这个可以作为判断他错的依据吗？

生9：我认为生2是正确的，我们把12拆成4×3，先算4×25=100，再算3×100=300;这是根据乘法结合律来就算，如果要按乘法分配律来计算就应该跟生3、生4、生5那样。（学生们都异口同声赞成生9的看法）

师：每一位学生都说一说你这样算的想法？（大家纷纷介绍自己的计算方法）

师：看来对于这道题，同学们是仁者见仁，智者见智啊。现在我们比较这五种方法，你认为哪种方法对我们来说比较方便，你喜欢哪种算法？（较多学生都赞同生2、生3的方法）

这里教师通过设计问题情境，不断追问，让学生思维碰撞，并提供一个独立思考表达想法、同伴互助分享思维的学习平台，让学生大胆交流展示自己的计算方法，也去倾听别人的想法，这样既审视了别人的做法，又反思了自己的方法，让学生在比较分析、交流分享的过程中，优化出简洁的计算方法，并内化为自己的认知，同时也经历了解决问题策略的多样化和优化过程，达到了“润物细无声”，巧妙渗透数学优化思想的效果。

三、自主导学，让学生在分享中体味数学转化思想

转化思想是解决问题的一种最基本、最常用的思想方法。在计算教学中巧妙渗透转化思想，可以将复杂转化为简单，陌生转化为熟悉，未知转化为已知。如，小数乘法转化成整数乘法计算、分数除法转化成分数乘法计算、异分母分数加减法转化成同分母分数加减法计算，等等。因此，笔者尝试让学生通过自主导学，分享发现，体会转化思想。

如，五年级下册探究异分母分数的加减法，为了让学生更好地探究异分母分数加法算理，笔者创设情境引出算式：+，让学生观察这道算式有什么特点，是否会计算。大多数学生都表示分母不相同不能相加。笔者大胆尝试，给学生设计了一张《学习记录单》（如图3），让学生根据自己的理解和经验，尝试寻找+的计算方法，然后在小组里交流自己的想法。教师巡视，并收集方法，学生依次上台展示交流自己的思维导案（如下）。