三维非轴对称直流电弧射流过程数值模拟

徐 龙，李秋菊，马文会，魏奎先，吕国强，邢爱民

(1.昆明理工大学 冶金与能源工程学院，云南 昆明 650093；2. 昆明理工大学 省部共建复杂有色金属资源清洁利用国家重点实验室，云南 昆明 650093； 3. 上海大学 省部共建高品质特殊钢冶金与制备国家重点实验室，上海 200444； 4. 云南能投化工有限责任公司，云南 昆明650093 )

0 引 言

电弧炉(EAF)生产工艺广泛应用于铬铁、铁镍、镁、二氧化钛、铂族金属、锌等的生产，目前该工艺占世界粗钢总产量的40%.电弧炉在生产过程中有两种技术：直流(DC)系统及交流(AC)系统.与传统的交流电弧炉设备相比, 直流电弧炉具有许多优势,如降低了能源和电极消耗，防止闪变效应以及降低噪音水平等，目前在全球范围内投入使用的新电弧炉大约有70%采用直流技术[1].同时，直流电弧炉的容量也在不断增大，目前投产的直流电弧炉大都在100 t以上，其单位变压器容量一般在1 000 kVA/t以上[2].

电弧炉是将电能转换为熔化炉料所需的热能的热工设备，如图1所示.直流电弧炉通常由一个圆柱形壳体组成, 炉衬有冷却元件和耐火材料.石墨电极从顶部进入容器，原料材料通常通过顶盖的位置处送入容器,并通过向炉内输入电力将炉料加热到熔化.与进料同时引入的化学还原剂能够与熔融材料发生非常迅速的反应，从而产生所需的产品.

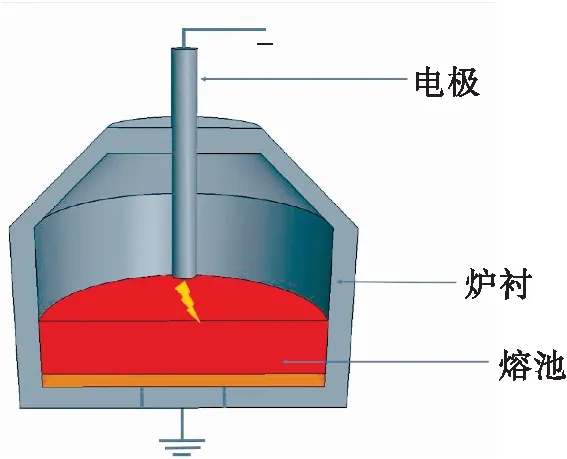
图1 直流电弧炉示意图

炉的主要能量来源是直流电弧，电弧在石墨电极的末端和导电熔池的表面之间撞击.等离子体电弧通过电阻电加热来提高电极和熔池之间气体的温度，一旦气体的温度达到一定的临界点(约5 000 K)，它的组成分子和原子开始电离成带正电荷的离子和带负电荷的电子，产生一个中性但非常强导电的等离子体气体.这种导电材料使电流从炉电极到熔池形成一个完整的闭合电路.由于电弧附近的极端环境，在系统上进行测量和实验非常困难，因此，开发系统的数值模型成为了研究与直流等离子体电弧相关的关键行为的最佳方法.Ushio[3]和Szekely等[4]首次尝试用数学方法描述电弧区的流体流动和传热，求解湍流的Navier-Stokes方程和能量方程，他们首先分析了电弧到熔池的不同传热机制的贡献.由Szekely等[4]提出的直流等离子电弧炉的分布参数数值方法随后得到了许多研究学者的进一步加强和扩展，而后Zhu[5]、Shamsi[6]、Qian[7]、Alexis等[8]引入了完全耦合的电磁场计算，以消除与经验指定的电流密度相关的不确定性.在这些求解中，电势和电流密度由产生于电磁学原理的偏微分方程描述，并与流场和温度场一起数值求解.Alexis[9]和Ramirez等[10]考虑了这一方法的变化，并重点讨论了在磁输运方程中包括感应电流项的问题.以上众多学者在直流等离子体电弧系统上进行的绝大多数建模工作主要集中在稳态二维轴对称模拟上.等离子体电弧系统实验研究有关的大部分学术工作表明，电弧经常处于不稳定的瞬态运行模式[11-12].在这种模式下，电弧快速移动，并在空间中形成复杂的形状，这是近似稳态建模的研究无法做到的.这种不稳定的行为会对直流电弧炉设备的运行产生重大影响，这既包括控制和测量系统的困难和灭弧等直接影响，也包括噪音污染等间接影响.

考虑到这一点，基于之前的研究基础，本文主要研究的是三维直流等离子体电弧射流现象.这些现象依赖于时间，包括振荡和螺旋电弧柱的发展、电弧非对称性和不稳定性，并且对表征电弧的相关物理场之间的耦合作用做了分析.

1 电弧射流数学模型

1.1模型假设

流体宏观模型认为流体是由无数流体元组成的连续介质，对流体元的质量、速度及温度进行统计平均可以获得流体的宏观性质参数.磁流体动力学理论是将等离子体看成导电流体，研究其宏观性质，能够得到不少的比较符合实际情况的结果，而且计算大大简化.等离子体电弧射流是一种非常复杂的物理现象.为了简化数学模型，基于磁流体动力学的理论，做了以下假设：

1)假设电弧处于局部热力学平衡(LTE)，这意味着电子和重粒子的温度没有明显的差别；

2)假设等离子体是光学薄的，因此可以使用单位体积的光学薄辐射损失来计算辐射；

3)假设熔池表面是平坦的；

4)忽略电极和熔体表面的金属蒸气对等离子体性能的影响[13-14].

电弧引起的高强度流动是湍流的，采用标准k-模型对湍流场进行表征.电弧等离子体由电弧炉中的空气组成，其物理性质即密度、粘度、导热系数、热容及等离子体(空气)的电导率，在模型中被视为与温度相关的函数[15].

1.2 控制方程

根据上述假定，从质量、动量和能量守恒出发，在三维笛卡尔坐标系下，给出如下电弧的控制方程：

连续性方程:

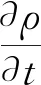
(1)

动量方程:

(2)

能量方程:

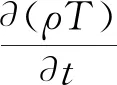
(3)

湍动能k方程：

(4)

耗散率ε方程：

(5)

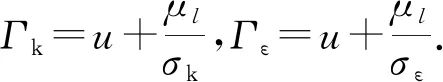
式(1)～式(5)中：ρ为密度；p为压力；T为温度；t为时间；U为速度矢量；B为磁通密度矢量；J为电流密度矢量；σ为电导率；SR为热辐射损失；μ为动力粘度系数；μl为湍流粘度系数；e为电子电荷；kb为Boltzmann常数；Pr为普朗特数；常系数C1ε、C2ε、Cμ、σk、σε的取值分别为1.44、1.92、0.09、1.0、1.3[16].

电磁场的影响以电磁力、焦耳热的形式作为源项添加到动量和能量控制方程中.为此还需求解描述电磁场的控制方程组，其描述如下：

(6)

式中：J为电流密度矢量，U为速度矢量，ø为电势，A为磁矢量势，μ0为真空磁导率，B为磁通密度矢量.

2 数值计算

2.1 计算区域与边界条件

目前，对直流电弧射流求解的模拟的验证，多与Bowman[17]对电流为2 160 A的空气中自由电弧等离子体燃弧所测实验数据进行验证对比.为此，采用FLUENT软件对该实验进行仿真求解并与实验数据进行对比，以求验证本文模型的可靠性.

2.1.1 计算区域

在实验中，鲍曼采用一种基于“钢球偏移技术”的实验方法对位于直径为 5 cm的石墨阴极和直径为15 cm的石墨阳极之间的自由电弧的速度场进行了测量，通过测定钢球的位置偏移量和一系列的公式推导来得到电弧射流的流场分布，实验时电弧弧长的取值为7 cm，电弧电流的取值2 160 A[18].图2为该实验的仿真计算区域示意图，炉体①和石墨电极②均简化为圆柱体，炉体高HCD=7 cm,直径øC1=15 cm,石墨电极直径øC2=10 cm.表面命名：炉底阳极表面为S1；石墨电极下表面(不含S3)为S2；阴极斑点为S3；炉体剩余表面为S4.

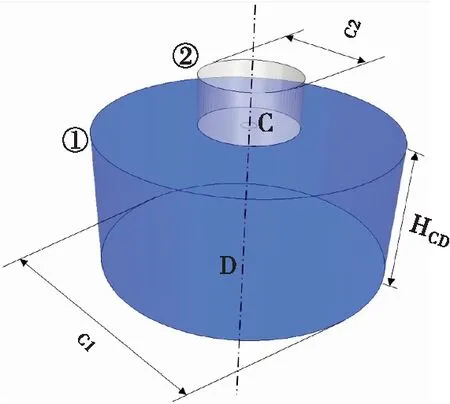
图2 仿真计算区域示意图

2.1.2 边界条件

几何模型建立后，为了获得相应问题的数值结果，还需要指定相关变量沿计算区域的边界条件，图2的边界条件设置如表1所示.

表1 三维电弧模型边界条件

假设电弧及其周围形成一个封闭系统，完全包含在计算域内,那么可以将炉体区域的边界视为壁面条件.因此可以指定速度的简单边界条件：无滑移壁面.温度边界条件是通过在所有表面上使用恒温来定义传热边界条件，主要根据模型边界上可能的不同墙体材料指定不同的温度，在此设定为2 000 K.阳极和电极上的温度由它们所组成的材料的蒸发温度来控制，因为与这些边界相比，电弧的温度要高得多，所以这些表面的温度将主要由表面材料转变成气态的相变来控制,即T=T∞.电极采用的是石墨材料，在计算中设置TC=4 100 K，低于碳的沸点(4 700 K)，是合理的；阳极设置为Ta=1 500 K，主要依据的是所要熔融物料的熔融温度.直流等离子体电弧另一重要的方面是电磁场的产生及其相互作用.电磁场受麦克斯韦定律支配，同时等离子体电弧中电导率是温度的强函数，提供了各种输运现象之间的基本耦合.电场边界条件通常设置表面上的固定电流或表面上的固定电流密度.对于直流等离子体电弧问题，阳极通常设置接地ØS1=0;阴极斑点内为固定电流密度jk，其余均认定为电绝缘.电流能够从电极表面顺利导通到气体中，主要是受制于电极表面热电子运动.根据Richardson-Dushman Equation：

(7)

式中：Ac的值主要取决于电极材料，石墨电极一般为60 A/(cm2·K2)；Tc为发射表面温度，即阴极表面温度；e为电子电荷；kb为Boltzmann常数；Wf为发射表面功函数，石墨电极的功函数为4.4 eV.对于固定的Tc,依据上述方程即可确定表面电流密度jk,同时可以确定阴极斑点半径rc：

(8)

式中：rc为阴极斑点半径，I为电弧电流.磁场求解是利用磁矢势的方法，也是目前普遍使用的方法.电弧炉的外侧壁和炉顶通常由钢或其他铁磁材料制成,起到非常有效的屏蔽作用，防止容器内部的磁场散发到周围的空间.因此可以认为周围的边界是磁绝缘的，即磁通线只允许在电流流经的边界部分进出计算区域.

2.2 耦合分析与网格划分

由流体流动、能量和电磁模型所体现的完整直流等离子体电弧模型展示了各种场之间的许多重要耦合效应，正是这些耦合效应导致了弧的形成，并随着时间的推移而持续下去.因此，对模型中存在的相互耦合作用提供一些附加的分析对进一步的理解是有必要的.图3给出了三者之间的耦合关系.

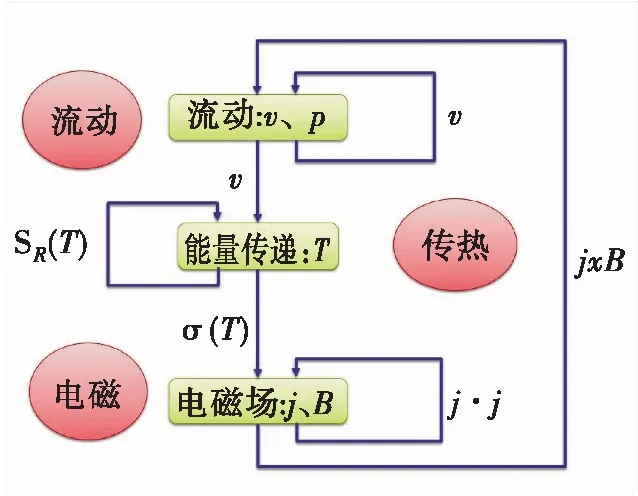
图3 多物理场耦合流程图

能量转移并不明显影响流体流动，但它非常强烈地影响电场和磁场，通过洛伦兹力作为外力源项反馈到流体流动方程中.同时，电磁场所带来的等离子体电阻加热，作为能量源项又影响着能量转移.能量自身也存在耦合，热等离子体气体发出的热辐射耦合效应通过能量吸收项体现.

首先对该计算区域进行网格划分，对电弧区域进行网格加密，网格划分结果如图4所示；然后采用有限体积的方法对控制方程进行离散求解.

图4 计算区域网格

3 结果与验证

本文输入电流采用2 160 A进行求解.时间t=1 ms之后，电弧开始出现不稳定性，射流速度开始下降，电弧开始扭曲旋转变形，为此可以认为在1 ms时达到稳定.

3.1 模型验证

在t=1 ms时，温度等值面分布如图5所示.采集该时刻炉体中心线处电弧温度和速度在Y方向上的分量值与Bowman[17]实验数据进行对比.由图6可以看出，二者基本吻合，初步验证了本文模型的可行性.继续进行求解，在1 ms后电弧开始出现不稳定性变化.

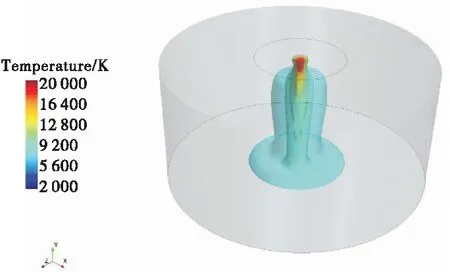
图5 1 ms温度等值面图

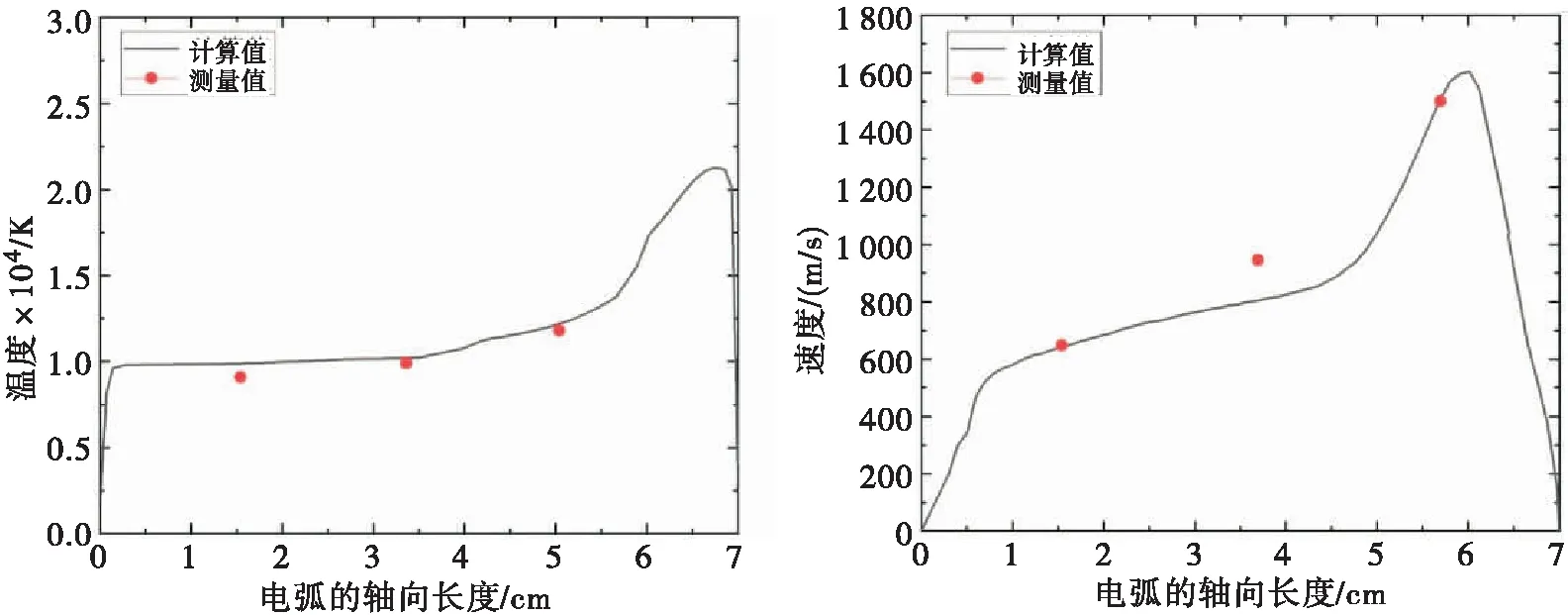
(a)电弧轴向温度分布 (b)电弧轴向速度分布

3.2 直流电弧射流行为3.2.1直流电弧的射流形态

直流等离子体电弧中包含流体动力学的描述模型，对于系统的完整模型的建立至关重要.电弧是由流动与其他物理现象相互作用驱动的高速气体射流,实质上是一个流体流动问题.在三维模型中，能够完整展现出阴极点附近流体更复杂的运动，图7显示了时间分别为2 ms和10 ms的流场.流线显示了流动的矢量行为.流线显示等离子体被吸引到阴极点附近的电弧中，沿着柱状物向下行进，并随着射流到达阳极表面而改变方向再循环到该区域，即：①→②→③→①.该运动表现为阴极点表面初期的合理规则的振荡到后期的无序混乱振荡.弧根的这种运动变化导致电弧喷射方向在靠近该点处旋转，这一影响又在电弧体下方的流场继续发展，最终生成螺旋形状.正如计算结果所得到的，随着初始条件的衰减，系统最初形成伪稳定弧，但是随着计算的进行，稳定性下降，偏弧行为开始发生.

(a) t=2 ms (b) t=10 ms

电磁场集中在阴极斑点表面附近如图8～图9所示.阴极斑点表面是该区域的最高电压点，磁场亦是如此，场的梯度在靠近下表面处也变得更大.在下表面处，阳极温度较低，到达其附近的等离子体气体被冷却，温度下降，同时其电导率降低.由于电势场在空间中的分布受与温度相关电导率的控制，靠近该区域的中心，电弧柱的连接导致温度升高，同时导致电势场梯度在电弧彼此接近的点附近被高度压缩到阳极表面.

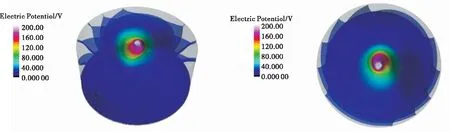
(a)主视图 (b)俯视图

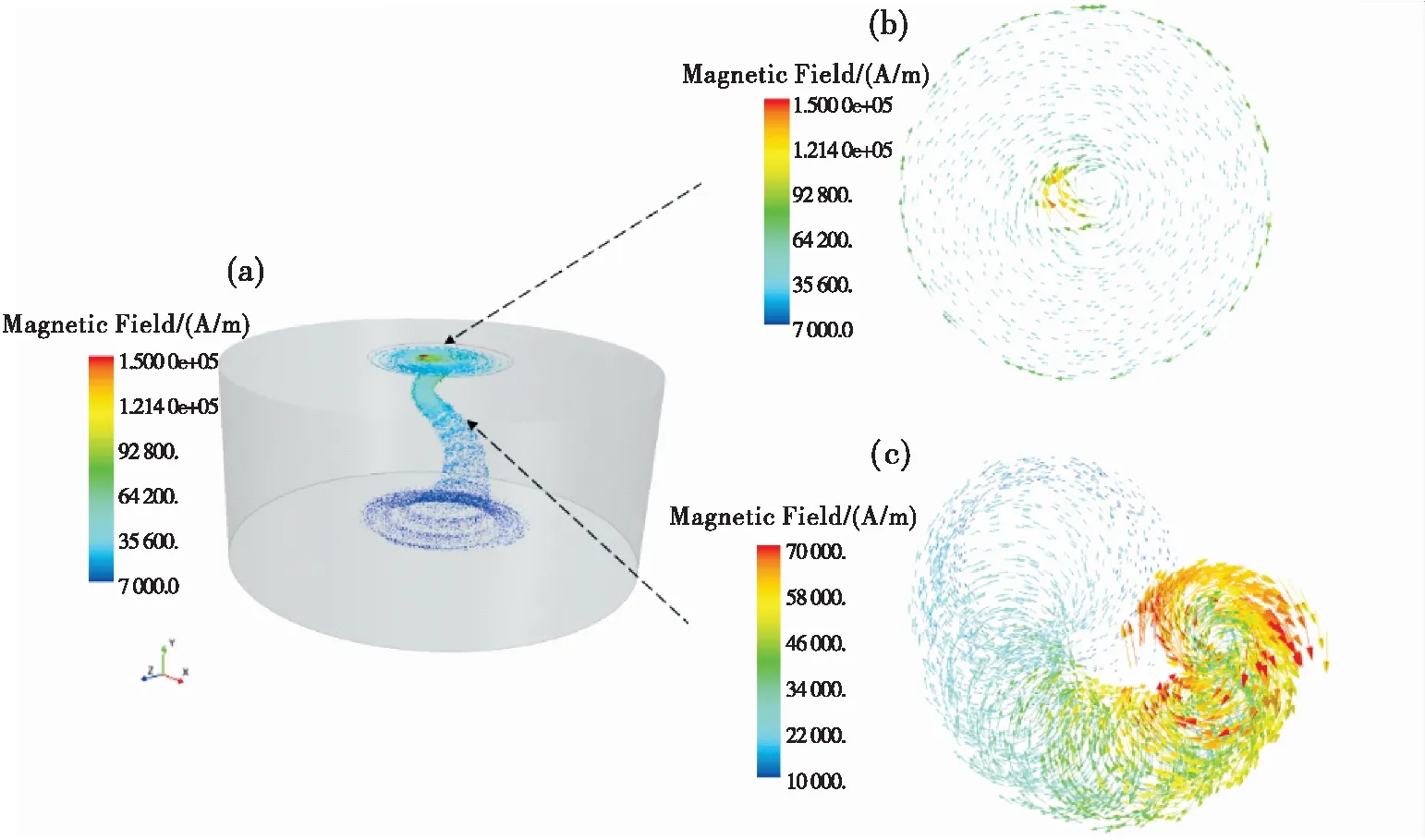
(a)全域磁场；(b)电极表面磁场；(c)弧柱磁场

3.2.2 温度场

图10显示t=10 ms的三维温度场，可以清楚的看到，三维模型更加准确地表示了弧柱与其附近空间的相互作用，显示了电弧柱的螺旋结构.该电弧柱是由阴极斑点表面附近的瞬态行为产生的，电弧在阴极点附近有一个高温的电弧根部区域，将高温气体沿电弧射流向下逐步扩展演变，形成特征柱状.

(a)主视图 (b)弧柱视图 (c)俯视图

t=10 ms时,固定三个维度中的两个，并沿着剩下的一个进行数据采集，可以对获得的数据进行更定量的可视化.对阳极表面上方不同高度的温度场进行采样，可以显示弧形柱的弯曲形状如图11(a)和图11(b)所示.图11(a)固定y=0 m,z=0 m,沿x轴提取数据；图11(b)固定y=0 m,x=0 m,沿z轴提取数据.当从上表面移动到下表面时，温度峰值给出了高温电弧射流中心线位置的估计.离阴极弧根越近电弧温度越高，对比图11(a)和图11(b)可以明显看出图11(a)中y=0.01 m处的温度高于y=0.03 m处的温度，而在图11(b)中是相反的，弧的射流中心发生偏转，充分说明了电弧的不对称性偏弧现象.

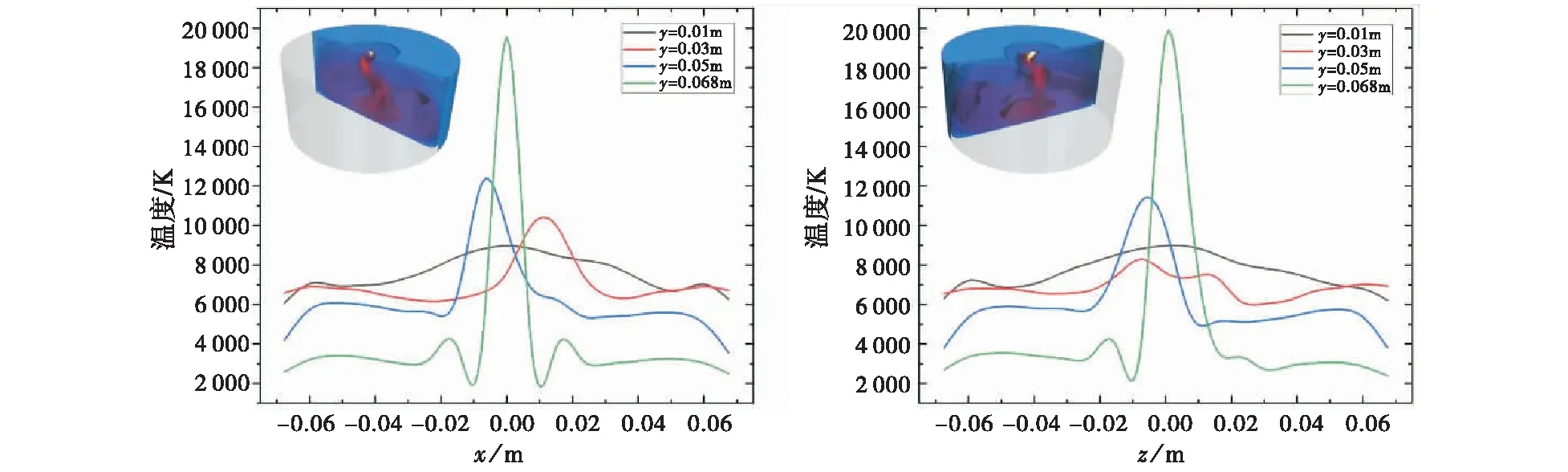
(a)z=0 m (b)x=0 m

在模拟过程中，对不同时间中轴线处速度场的y分量数据进行监测，显示了由过渡到非稳态运动所产生的变化.由图12可以看出，随着电弧的瞬态行为变得越来越动态，更多的能量被转移到螺旋进动运动中，阳极方向上的射流的峰值速度显著下降.

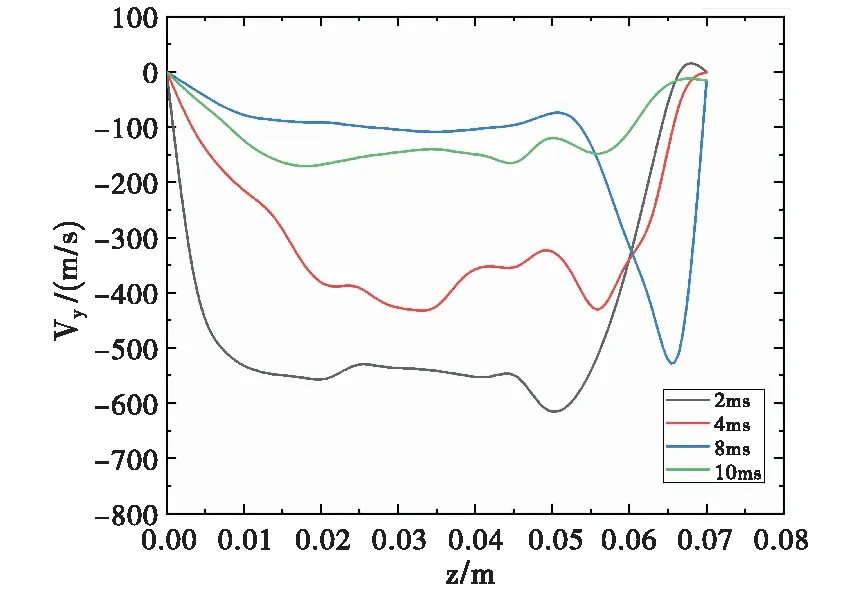
图12 中轴线处不同时刻速度在y方向的分量

为了研究三维等离子体电弧模型中某些位置的场的可变行为，考察阴极斑点表面下2 mm的位置处G点温度变量随时间的演变，如图13所示.三维模型初期呈现高度规则的振荡，后续发展到无序混乱的振荡.这里发生的电弧不稳定性的本质与电弧射流围绕每个阴极点表面的规则运动有关.它产生了电弧的螺旋形状以及在靠近阴极点的温度变量中观察到的规则振荡行为.对同样位置电势进行采集得到图14，获得了和温度场同样的现象.电势场的变化在一定程度上抑制了温度以及电导率的巨大变化，但振荡仍然可见，随着时间推移，电势出现较大的振荡，同时导致了温度的巨大变化和不稳定性.

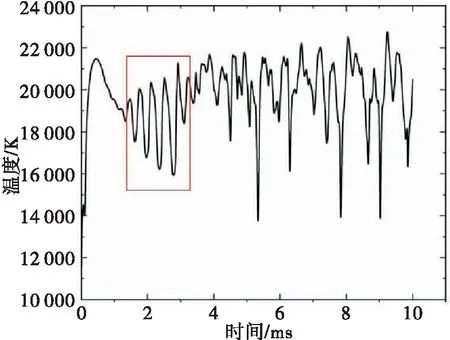
图13 G点温度随时间的变化

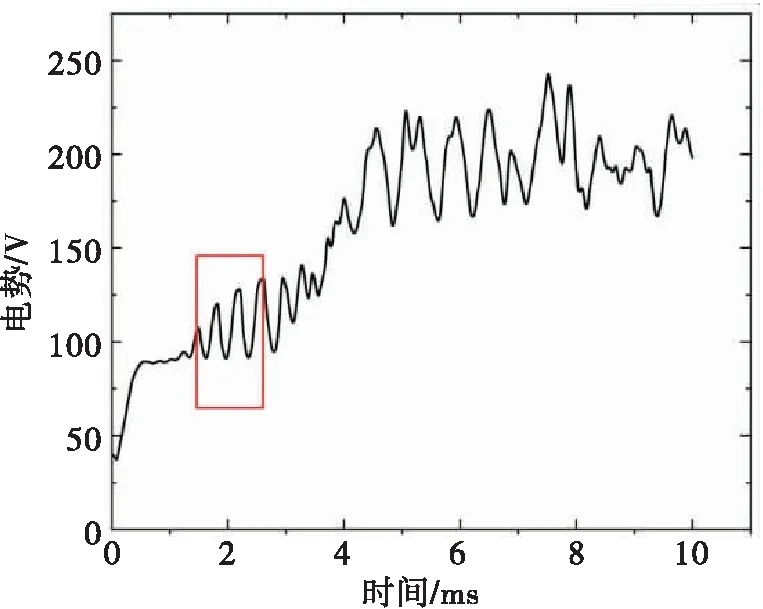
图14 G点电势随时间的变化

4 结 论

本文研究了三维直流等离子体电弧炉射流的动态行为.模型以速度、温度和电磁场的时间相关数据描述三维电弧系统的演化.计算了速度、温度和电弧电压的值，并与早期的实验数据进行了比较.对三维直流电弧的模拟研究表明:

1)电弧射流最初表现为直的、稳定的圆柱形柱，但是阴极点附近的不稳定性导致发生振荡，并最终导致电弧射流围绕阴极点偏移，产生螺旋状非对称结构，这是电弧的一种不稳定和持久的动态行为.

2)由于电弧起弧的时间尺度非常短，许多定义电弧的耦合多物理场产生的现象不容易通过实验测量或量化.在没有测量的情况下，这样的计算模型可以帮助进一步理解直流等离子电弧如何作为一种耦合的、电磁驱动的流体流动现象，这类知识对电弧炉系统的控制和操作有很大的帮助.