面向深度调峰的火电机组灵活性改造规划模型

杨寅平，曾 沅，秦 超，王成山

（智能电网教育部重点实验室（天津大学），天津市 300072）

0 引言

可再生能源大规模接入电网，对电网调峰能力提出了更高的要求。以中国现有的电源结构，无论装机容量还是发电量都是以火电为主，故利用火电机组进行深度调峰仍是当前电网的主要选择［1-2］。在火电机组参与深度调峰时，需要提前进行灵活性改造以降低机组的最低出力极限。文献［3］构建了适用于大规模风电接入场景下的火电机组灵活性改造规划模型，在优化目标中计及了改造、发电和弃风成本，并采用Benders分解法实现了模型的高效求解。文献［4-5］从技术角度分析了影响火电机组调峰能力的主要因素，提出了火电机组在各调峰阶段中的能耗成本模型，并详细分析了火电机组在不同调峰深度下对系统产生的影响。目前，研究工作仍集中于火电机组在实施不同灵活性改造方案下的系统经济性分析，网络拓扑结构对灵活性改造规划所造成的影响以及方案在多个场景下的适应性等仍有待进一步深化研究。

综上，结合火电机组在深度调峰阶段的运行特性，本文提出了一种基于区间整体优化［6-9］的火电机组灵活性改造规划模型，该模型具有如下特性。

1）在模型中引入了火电机组在深度调峰不同阶段运行中的详细成本模型，包含了显性的燃料费用和用于稳定锅炉燃烧的柴油费用，以及隐性的机组损耗费用［4-5］。因此，所构建的成本模型更加贴近实际运行中的经济特性。

2）火电机组运行在深度调峰阶段中的单位发电成本大幅上升，选择以非投油调峰方式和投油调峰方式来消纳风电，或者选择弃风均会对系统运行费用产生较大影响。针对这一问题，在模型中引入了区间优化方法，以结合多个场景运行费用以及机组改造费用的年综合费用区间作为优化目标，并使用2个步骤来实现求解。首先，使用多领头群优化（group search optimizer with multiple producers，GSOMP）算法［10-12］来协同优化目标区间的2个特征量，得到多个具有不同目标区间特性的候选方案。其次，使用多属性决策（multiple attributeddecision making，MADA）方法［13-14］对各个候选方案的目标区间进行综合评估，从而得到一组综合经济性最优的方案。

3）需要火电机组进行深度调峰的电网往往接入了高比例风电，这些风电的高不确定性极易造成各运行场景下的潮流阻塞，尤其在风电极限送出场景下。所提出的模型以区间优化方法实现了全场景优化，特别考虑了各风电极限送出场景下的潮流优化，从而提高了模型所提供方案的潮流适应性，有效减少了各场景下由于潮流阻塞所造成的弃风量。

1 火电机组灵活性改造规划模型的建立

1.1 火电机组调峰成本模型

依据不同的调节能力和成本特性，火电机组的运行过程可以分为常规调峰（regular peak regulation，RPR）、非投油调峰（deep peak regulation without oil，DPR）、投油调峰（deep peak regulation with oil，DPRO）3个阶段。如图1所示［4-5，15］，Pa、Pb、Pc、Pmax分别为机组在RPR、DPR和DPRO阶段的最小技术出力以及最大出力。

图1 火电机组调峰过程示意图Fig.1 Schematic diagram of peak regulation process of thermal power units

在RPR阶段，火电机组的运行成本仅包含煤耗费用，该费用通常基于煤耗特性函数f(·)进行计算，如式（1）所示。

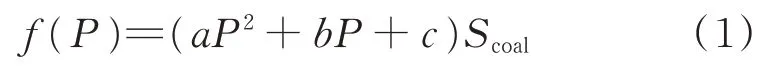
式中：a、b、c分别为机组耗量特性函数的二次项、一次项、常数项系数，其取值与机组类型、锅炉型号和煤质有关；Scoal为当季的单位煤炭价格；P为机组有功出力。

在DPR和DPRO阶段，深度压低机组出力会造成转子轴系热应力过大，引起转子低周疲劳损耗和蠕变损耗，进而导致机组本体发生严重的变形和断裂，缩短机组寿命。汽轮机转子寿命的计算是一个非常复杂的问题，现有研究中尚无公认的计算公式可以有效解决。本文将按照转子材料的低周疲劳特性关系进行低周疲劳寿命损耗计算。

Manson-coffin公式体现了总应变幅度与转子致裂循环周次的关系，其函数关系为：

式中：σf为材料的疲劳强度系数；qf为材料的疲劳延性系数；d为材料的疲劳强度指数；e为材料的疲劳延性指数；Nt为时刻t转子致裂循环周次，与机组出力P有 关；Δεt为 时 刻t转 子 总 应 变 幅 度；E为 弹 性模量。

根据机组转子的应力及离心切向应力可得到转子的总应变幅度Δεt，代入式（2）可以确定转子致裂循环周次Nt，再结合机组购机成本可粗略得到机组的损耗费用wcost(P)为：

式中：Sunit为机组购机成本。

在DPRO阶段，锅炉的燃烧稳定性、水动力工况安全性都迅速下降，会出现无法稳定燃烧的情况，机组需要投油助燃以保证机组的安全运行，投油费用woil为：

式中：Scost为机组当季燃油价格；Zoil为机组投油量。

综上，火电机组在不同调峰阶段中的运行成本具有不同的特性，详细的火电机组运行成本可以表述为如下的分段函数：

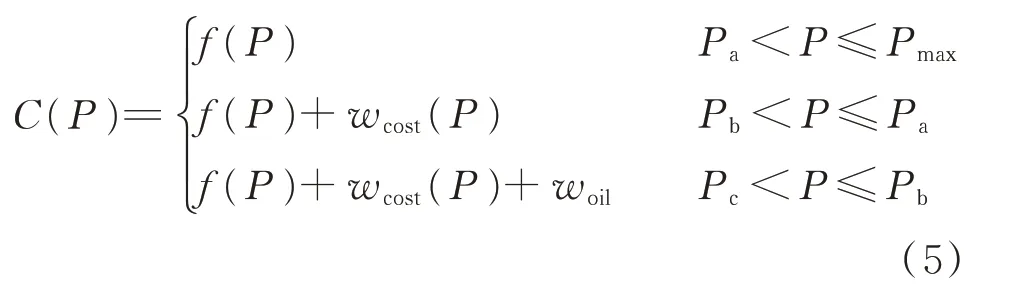
式中：C（P）为火电机组的运行成本。

式（5）中f(P)和woil均属于显性成本；wcost(P)属于隐性成本。

1.2 火电机组灵活性改造规划确定性模型

所建立的火电机组灵活性改造规划确定性模型，综合考虑了火电机组的灵活性改造费用以及改造后的运行费用。为了便于长期规划及运行中计算周期的统一，将模型的优化周期选择为1年，即以年化改造费用和年运行费用的年综合费用作为模型的优化目标。该模型具体表述如下。

式（6）表示模型的优化目标为最小化年综合费用，包括了年化改造费用和年运行费用。式（7）给出了火电机组年化改造费用的公式。式（8）给出了单位容量的年改造费用的折算公式。式（9）给出了系统中年运行费用的公式。式（10）为系统中的功率平衡约束。式（11）为火电机组的出力约束。式（12）和式（13）为火电机组的灵活性改造约束。式（14）为火电机组的爬坡约束。式（15）为线路潮流约束。式（16）为风电机组的弃风量约束。

该模型可以表示为如下的通用形式：

1.3 火电机组灵活性改造规划区间模型

较之传统的火电机组，风电机组的出力具有较强的波动性，这导致实际计算中风电的出力存在较高的不确定性。当多个风电场在各时段出力范围区间内波动时，将产生多个不确定场景，不确定场景s可表示为：

从给出的场景s表达式Ps，m中可以看出，考虑到多个风电场的波动性后，会衍生出大量的不确定场景。在系统中存在大量不确定场景的情况下，区间方法通过限定各个节点不确定场景的波动范围，进而限定场景集的边界，边界范围内可以覆盖所有过渡场景中的值。所提出的模型旨在寻找一组火电机组灵活性改造方案，使之能够满足在多个运行日中风电波动范围内电网潮流可行并具有最优的经济性。

原模型中的式（9）—式（11）、式（14）—式（16）可以转换为区间形式，其表述形式以及相应的场景削减方法如下。

1）系统运行费用

年运行费用区间的上、下限分别如式（20）和式（21）所示。

2）功率平衡等式

系统中的功率平衡等式由4个部分构成，分别为火电机组出力、风电机组出力、负荷以及弃风量。由于风电机组出力及负荷功率都是一个已知量，故可将该已知量转移至等式的等号右侧，从而反映未知量的出力范围。

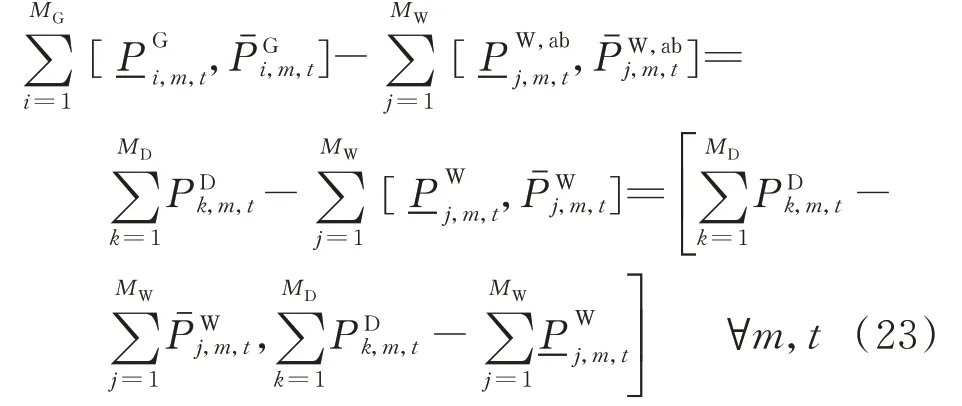
将式（23）等号左侧2个区间的上限值和下限值分别进行结合，可以得到2个极限场景，该区间等式可以转换为如下2个极限场景下的功率平衡等式。

依据区间不等式的上限、下限严格约束，可以将式（26）转换为以下2个不等式。

4）爬坡约束

通过对这2个区间的上限、下限进行约束，可以将式（29）转换为以下2个不等式。

5）线路潮流约束

将该区间不等式的已知量与未知量分别转移至不等式的两侧，并将该双侧不等式转换为2个单侧不等式以便于求解，可得：

对于等式右侧的已知量，依据低边界理论对区间边界进行缩紧，选择不等式右侧的最小量作为边界的缩紧条件，该条件为加于线路潮流中的最紧约束，可以保证所有可能场景下的潮流可行。对于等式左侧的未知量，依据区间的上限、下限进行约束。通过上述过程，可以将2个不等式转换如下。

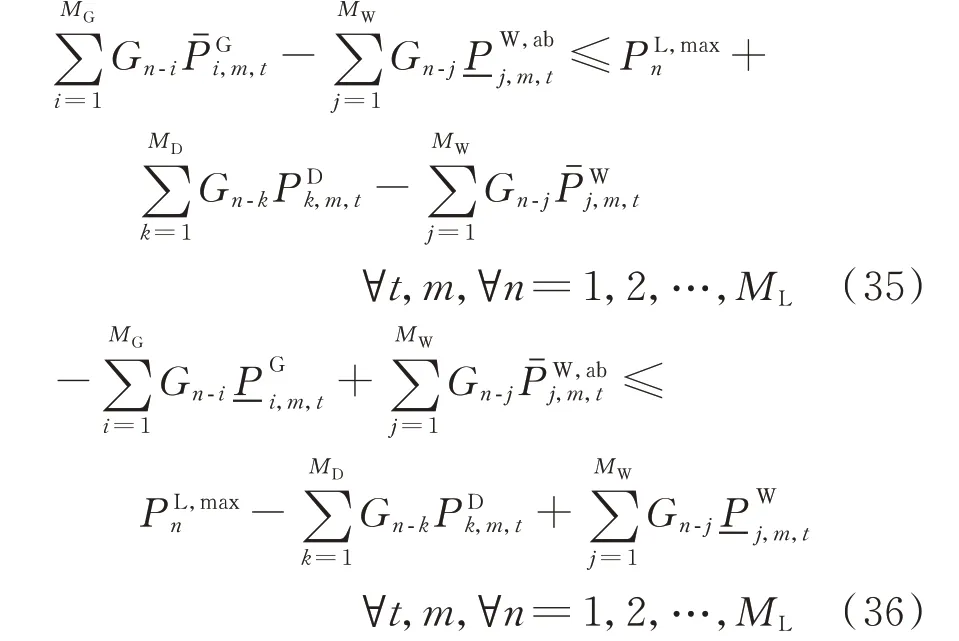
6）弃风约束

对于该区间不等式，只要对2个区间的上、下限分别进行约束即可保证所有场景均可满足要求。该不等式可转换为以下2个约束。

综上所述，原有模型中的约束条件以及目标函数可以由区间形式来表述，并可以通过严谨的数学推导来进行全场景削减，确保各区间范围覆盖了所有可能的过渡场景。原模型可以表述为如下的通用形式：

所提出模型的优化目标中共包含2个部分，一部分是火电机组的年化灵活性改造费用，是一个单值目标；另一部分是在给定风电出力预测区间下形成的年运行费用区间，是一个区间目标。为了便于计算，合并这2个部分的费用得到年综合费用区间。为了综合衡量目标区间的整体特性，使用区间均值和偏差值作为区间的特征量来进行协同优化。原模型可以转换为［9，11，16］：

2 火电机组灵活性改造模型求解方法

本文中将所提出的火电机组灵活性改造模型转换为一个多目标优化问题。多目标优化本质上是一个两阶段优化问题，包含多目标寻优和多目标决策2个阶段。在该模型的求解中，首先，使用GSOMP算法对所提出的模型进行多目标寻优，求解得到一组最优的非支配解集。其次，使用证据推理方法对解集内的每个解进行综合评估，依据用户的需求从解集中选择一个最优解。

2.1 基于GSOMP算法的区间优化模型求解方法

GSOMP算法［11-12］是一种基于群体搜索的多目标优化方法。该方法在寻优过程中模拟了蜂群智能搜索技术，因而在搜索非支配解集的应用中具有良好的表现。本文采用GSOMP算法求取一组侧重于不同子目标的非支配最优解集（帕累托解集），具体的计算流程如图2所示。图2中K和Kmax分别为迭代次数和最大迭代次数。

图2 采用GSOMP算法求解模型的流程图Fig.2 Flow chart of model solved by GSOMP algorithm

2.2 基于证据推理的目标区间评估方法

采用GSOMP算法对所提出的模型进行多目标寻优可以获取一组非支配解集，该解集中包含了多个具有不同年综合费用区间特性的候选方案。本节采用证据推理方法对多个优化子目标进行综合评估，从多个候选方案中选择最优方案。

证据推理方法是一种基于属性的三层启发式评估方法［13-14］，整体结构如附录A图A1所示。在评估框架的底层，定义了各待评估的基本属性Ii（i=1，2），每个基本属性具有一个相应的权重值αi（i=1，2），该模型中的基本属性即为年综合费用区间的均值和偏差值。在评估框架的中间层，共设置了5个评价等级Hn（n=1，2，3，4，5），分别为优秀、良好、一般、勉强和差。该层将各个基本属性划分至5个评价等级中并生成相应的等级置信度βn，i，通过结合各个基本属性的等级评估结果以及权重值，可以得到各方案在5个评价等级上的综合评估结果。在评估框架的顶层，将各个等级的评估结果以及相应的等级需求程度进行结合，就得到了方案的综合评估结果。

依据上述步骤对每个候选方案进行评估，并对评估结果进行依次排序即可得到一组最优方案，具体的评估方法如文献［9］所述。

3 算例分析

3.1 基础算例

本文以修改后的IEEE 39节点系统［17］为例，验证所提出的火电机组灵活性改造规划模型及其求解方法的有效性。该算例系统包含10台火电机组，装机容量共计6 512 MW；系统中拥有17个负荷节点，各节点负荷共计6 147 MW。该系统在节点28、30、37、38分别接入了1个风电场，容量均为700 MW。火电机组参数详见附录A表A1，机组的运行参数采用算例原始数据，机组的煤耗数据来自实际电网中的火电厂数据，煤炭价格和投油所用的柴油价格分别为550元/t以及6 130元/t，购机费用为火电厂的实际建设费用［1］。节点负荷数据详见附录A表A2，各月典型日的负荷数据来自实际电网，负荷在各时段的值则依据各节点的原始负荷情况按比例进行增减。风电场的出力采用某电网中的实际风电场出力，风电场出力的预测误差设置为20%，弃风惩罚费用为500元/（MW·h）［18］。火电机组损耗参数［15］见附录A表A3，该表显示了火电机组在不同调峰深度下的机组损耗情况。

火电机组在实施灵活性改造前的调峰容量为额定容量的50%［19］。按照不同的调节能力可将火电机组的灵活性改造方案分为2种，分别为非投油调峰改造方案和投油调峰改造方案，改造后的机组最低出力分别为额定容量的35%和20%。火电机组的灵活性改造费用为105万元/MW［20］，按照改造后机组继续运行20年、年利率6%进行折算，年化灵活性改造费用为8.8万元/MW。在模型的求解中，设置GSOMP算法中的最大迭代次数为60次，每次迭代中存储5个最优解，附录A图A2中给出了不同迭代次数下的最优非支配解集，以验证所设置的迭代次数可以保证足够的计算精度。在评估阶段设置了5个评价等级，分别为{优秀、良好、一般、勉强、差}，各个评价等级的划分标准表述如下：依次排序各个候选方案中的年综合费用区间和偏差值，选择最优值为优秀等级的评价标准，选择最差值为差等级的评价标准，其他等级的评价标准则依据最优值和最差值之间的偏差均分得到。各个评价等级所设置的效用值分别为{1.00，0.85，0.55，0.35，0}［13］。

3.2 基础算例仿真结果

在MATLAB软件中搭建所提出的模型，使用CPLEX求解器进行求解。所提出的模型以包含火电机组年化改造费用和多个不确定场景下运行费用的年综合费用区间作为优化目标。当协同优化目标区间的均值和偏差值时，可以获取6个非支配最优解，每个解代表一组火电机组灵活性改造方案，分别为方案A1、A2、A3、A4、A5、A6。

如图3所示，以所获取的6个候选方案A1至A6实施火电机组灵活性改造时，各组方案所形成的年综合费用区间呈现出不同的区间特性。方案A1具有最低的区间均值，方案A6具有最小的区间偏差值。从方案A1到A6，各方案中的区间偏差值持续降低，而区间均值则有所升高。年综合费用区间的均值和偏差值作为模型中的2个优化子目标，往往呈现相互冲突的关系。

图3 候选方案的年综合费用区间Fig.3 Annualized comprehensive cost intervals of candidate schemes

为了综合考虑和权衡各候选方案的年综合费用区间的均值和偏差值，使用证据推理方法进行综合决策。对各个候选方案的年综合费用区间的均值和偏差值分别进行等级评估，并结合每个区间特性所对应的权重值，得到候选方案在各个评价等级上的分布情况。依据等级评估结果以及所设置的等级效用值，可以得到候选方案的综合评估结果，即为综合效用值。在评估过程中，为了更好地计及各场景的运行费用，采用风电出力的概率分布生成3 000个随机场景，并依据年综合费用区间均值和偏差值的概率分布情况来实现等级评估。评估的具体步骤如文献［9］所述，评估结果如表1所示。将候选方案A1至A6的综合效用值进行排序可知，方案A2为所选择的最佳方案，综合效用值是0.70。

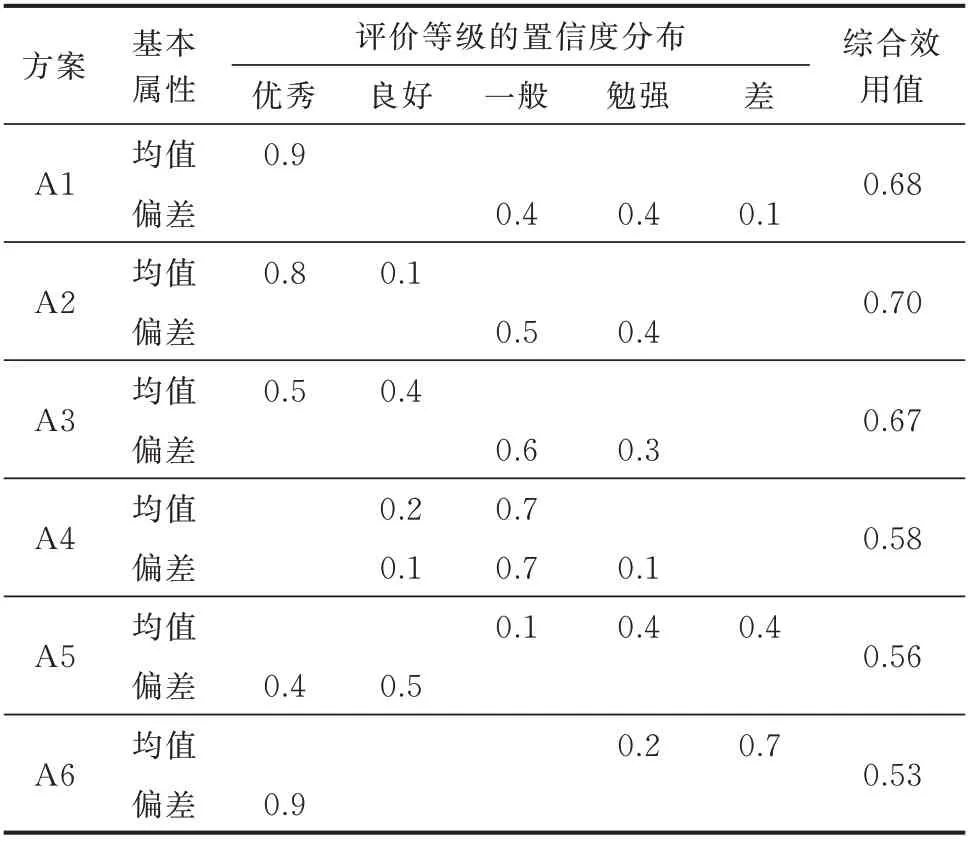
表1 候选方案的多属性决策结果Table 1 Multi-attribute decision-making results of candidate schemes

表2给出了火电机组G1至G10的灵活性改造的候选方案A1至A6。表3给出了各候选方案中的机组改造容量。表4给出了各个候选方案中的各项费用。如表3所示，方案A1至A6中实施了调峰改造的机组容量分别为1 166.4、1 068.9、996.0、934.8、832.2、769.8 MW，各组方案中的改造容量呈现逐渐减少的趋势。

表2 火电机组灵活性改造候选方案Table 2 Candidate schemes for flexibility reformation of thermal power units

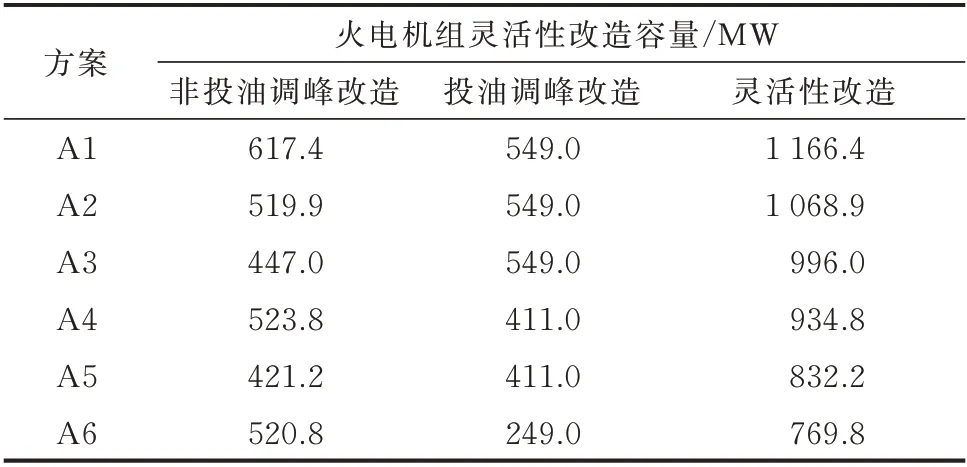
表3 候选方案的火电机组灵活性改造容量Table 3 Flexibility reformation capacity of thermal power units in candidate schemes

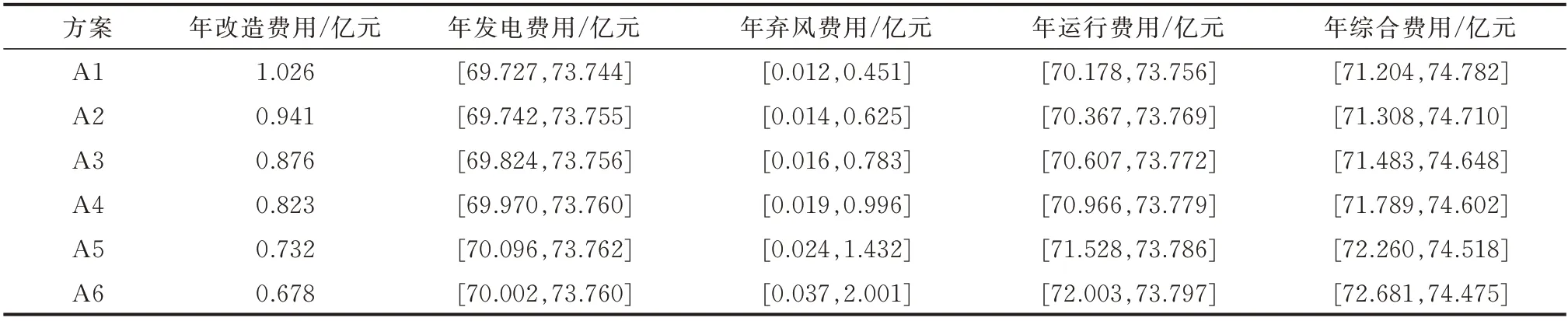
表4 火电机组灵活性改造候选方案的各项费用Table 4 Various costs for flexibility reformation of thermal power units in candidate schemes

方案A1具有最大的机组调峰改造容量，该方案尽可能地提高了系统中的风电消纳量，减少了所有场景中的弃风费用，但由于方案中的调峰改造容量相对较大，引起机组调峰改造费用的增加，造成方案的综合经济性有所下降。最优方案A2适当地削减了机组调峰改造容量，虽然在部分运行场景中弃风费用有所增加，尤其是在风电出力波动范围的上限，即风电大发场景下的弃风量最大，造成区间的下限略微上升，但大部分场景中的运行费用仍可以维持在较低值，结合方案中较低的机组调峰改造费用，该方案的综合经济性最优。方案A3至A6中的机组调峰改造容量进一步降低，系统中逐渐出现调峰容量不足的现象，各方案中的弃风量呈现大幅上升的趋势。由于弃风费用相对较高，故各方案中的运行费用也随之大幅上升，在方案A6中运行费用的增加已非常明显。虽然各方案中的机组调峰改造费用会相应地有所下降，但由于弃风所引起的运行费用上升则更为明显，造成各方案的经济性逐渐变差。

综上，在所得到的最优方案中提供了各机组的最优灵活性改造计划以及改造容量。并且该方案可以实现对系统中大部分风电的消纳，同时将部分造成经济性不佳的风电予以丢弃，有效地折中了机组改造费用以及多个场景下的运行费用。

3.3 算法比较

当火电机组在深度调峰阶段运行时，机组的单位发电成本明显上升，各运行场景中将面临单位发电成本不均衡的现象。本文以区间整体优化方法来综合多个场景下的运行费用，从而提高模型在各场景下的适应性。同时，区间优化方法以全场景方式进行优化，从而提高模型在高风电接入比例下的潮流适应性。为了验证所提出模型的有效性，与文献［3］中所提出的模型进行了对比，该模型中仅考虑了火电机组灵活性改造方案在各月典型场景中的适应性。表5给出了2种优化方法得到的最优火电机组灵活性改造方案。表6给出了2种最优方案中的具体改造容量。方案A2和方案B1分别代表区间优化方法和确定性优化方法所得到的最优方案。

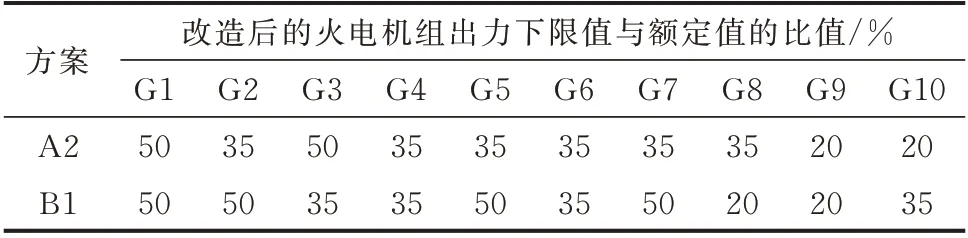
表5 两种优化方法下的最优火电机组灵活性改造方案Table 5 Optimal flexibility reformation schemes of thermal power units with two optimization methods

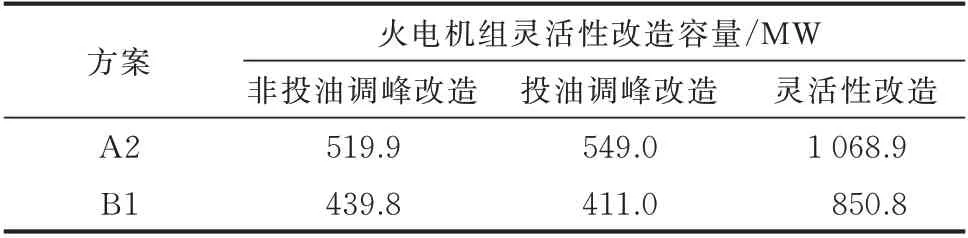
表6两个最优方案中的火电机组灵活性改造容量Table 6 Flexibility reformation capacity of thermal power units in two optimal schemes

图4给出了2种优化方法所得到的最优方案在不同风电出力场景中的年运行费用。如图4所示，在常规风电出力场景中，方案A2和方案B1的年综合费用相近；而在风电出力较大的场景中，方案A2的年综合费用则明显偏低。综合多个风电出力场景下的年综合费用，可表明方案A2的综合经济性更佳。为了更加直观地表明2个方案在不同风电出力场景下的运行经济性，选择了3个典型风电出力场景并将这些场景中的各项费用列于表7中。其中方案A2和方案B1的年化灵活性改造费用分别为0.941亿 元和0.749亿元。

如表7和图4所示，方案A2明显降低了风电出力较大的一些场景中的运行费用以及弃风量。该现象主要由2个原因造成：第一，风电出力较大场景中的火电机组出力较低，故这些场景中的运行费用将明显受到火电机组灵活性改造方案的影响，而在改造方案中选择非投油调峰改造、投油调峰改造或者弃风下的单位运行费用会存在2～3倍的差距，所提出的模型以全场景优化方式计及了风电出力较大场景中的运行费用，有效降低了这些场景中的运行费用；第二，所提出的模型考虑了全场景下的潮流优化，所得到的机组改造方案具有更好的潮流适应性。如表5所示，方案A2适当增加了风电送出侧的机组改造容量，从而有效降低了由于线路阻塞所造成的弃风惩罚费用。附录A图A3和图A4分别给出了方案A2和方案B1中风电送出侧线路1-2在冬季典型日中传输的有功功率，进一步说明了方案A2有效缓解了半夜时段和晚高峰时段的风电阻塞现象。

图4 两个最优方案在不同风电出力场景下的年综合费用Fig.4 Annualized comprehensive costs of two optimal schemes in different wind power output scenarios

表7 两个最优方案在不同出力场景下的费用Table 7 Costs of two optimal schemes in different wind power output scenarios

4 结语

本文提出了一个基于区间优化的火电机组灵活性改造规划模型。该模型以火电机组灵活性改造费用和多场景运行费用的年综合费用区间作为优化目标，并采用全场景优化方法来协同多个场景下的运行费用，从而得到一组综合经济性最优的火电机组灵活性改造方案。

所提出的模型提取了目标区间的均值和偏差值作为该区间的特征量，并将其选择为模型中的2个优化子目标。为了综合衡量目标区间的整体特性并筛选出最大限度满足用户需求的方案，在模型求解中使用了多目标寻优和多属性决策2个步骤。首先，使用GSOMP算法来协同优化目标区间的均值和偏差值，从而生成多个候选方案，每个方案具有不同的年综合费用区间特性。其次，使用多属性决策方法对各个方案中的年综合费用区间进行评估，依据各区间特征量的综合表现选择一组最优的方案。经算例验证，所提出的模型有效提高了方案的综合经济性以及潮流适应性。在经济性方面，由于火电机组在深度调峰阶段中的单位发电成本变化明显，故各不确定场景下的运行费用均将很大程度地依赖于改造方案。该模型采用全场景优化方法，明显改善了风电出力较大场景下的运行费用，并维持了常规风电出力场景下的低运行费用，实现了方案的综合经济性提升。在潮流适应性方面，全场景优化方式能够更好地适应高风电接入比例下的潮流不确定性，有效缓解了潮流阻塞现象并减少了各不确定场景下的弃风量。

需要说明的是，所提出的模型仅对机组灵活性改造的布点和方案进行了优化，并没有考虑机组改造停运所造成的影响。实际上，机组进行灵活性改造具有一定的停运周期，而这部分停运周期会对电网的安全稳定运行造成一定的影响，故机组的灵活性改造应遵循一定的时序性。因此，下一步计划开展具有时序特性的机组改造方案研究，以提供在保证电网安全稳定运行前提下可以逐步实施的火电机组灵活性改造方案。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。