基于风力发电机典型控制策略的控制参数设计及稳定性验证

朱 瑛，郭雅慧，王志聪

（河海大学能源与电气学院，江苏省南京市 211100）

0 引言

据国际能源署（IEA）和中国可再生能源学会风能专业委员会（CWEA）称，由于新型冠状病毒肺炎疫情的蔓延，为加速全球经济复苏，电力结构需更大程度地转向可再生能源以促进能源转型［1］。近些年，由于化石燃料等传统能源日益紧缺，风电发展迅速，风能成为目前世界上最成熟、最有前途的可再生能源之一［2］。2019年，中国风力发电量首次突破400 TW·h，占总发电量的5.5%［3-5］。随着全球的风电产能持续增长，风电技术将进一步发展。

然而，由于风速的随机性［6-8］，波动的风电功率会给电网带来电压或频率的波动，降低了电能质量，且会导致一系列的不稳定问题［9］。针对功率的波动，学者们提出了很多平滑方法，总体可分为间接功率控制、直接功率控制两大类［10-11］。

间接功率控制利用储能系统实现，只要引入足够大容量的储能就可显著减轻功率波动，同时不影响风力发电效率［12-13］。然而，加装储能的成本较高，且无法改善风力发电机端侧变流器所造成的功率波动。因此，研究依靠风力发电系统自身平滑输出功率的控制策略很有必要，即直接功率控制。直接功率可通过转子动能、直流母线电压、桨距角等来控制［14-16］。然而，直流母线电压控制引起的过大电压脉动会影响系统正常稳定运行［17］；频繁的桨距角控制往往会增大风力机叶片机械应力且会降低风力发电效率［18］；风力发电机转子较大的惯性能储存大量的能量［19-21］，调节转速来释放储存的转子动能可间接控制风力机输出功率。

文献［20-21］中研究了基于转子动能的功率控制策略，但是没有详细分析控制策略，且未考虑控制参数对风力机运行稳定性的影响。文献［22］从功率平滑的角度对恒功率控制、恒转矩控制和最大功率控制进行了比较，推导出了风速与输出功率间的传递函数，利用惯性能量来平滑功率，并分析了平滑的效果及稳定性，但没有给出频域中转速控制的优化设计。文献［23］基于改进最大功率点跟踪（MPPT）控制策略，在文献［22］的基础上建立了从风速到输出功率、转矩和转速的传递函数，深入考虑了频域中转速控制的优化设计，得到了控制器的优化参数，但未考虑风力发电机平滑策略变化对该优化设计的影响。针对控制器参数的设计和整定也有较多研究，文献［24］通过分析系统特征值和相关因子，研究得到全风况下系统特征根轨迹及相应振荡模式，为研究电力系统变换器和控制器的设计提供了理论参考。文献［25］通过研究双馈风力发电机变换器控制参数与系统特征根之间的关系，提出了使电力系统小干扰稳定的变换器控制参数设计方案。但是，上述研究均没有分析风力机稳定运行条件，也没有考虑优化参数的设计。

本文在控制器优化设计的基础上，深入考虑控制参数对风力机运行稳定性的影响，并进行了稳定性验证，分析了不同风力发电机控制策略在优化设计下的不同表现。首先，建立了风力发电机控制策略——改进MPPT和功率反馈控制下的传递函数，并提出了风力机的稳定运行约束条件。然后，对控制器进行了合理的优化设计，得到了控制器的优化参数，研究并保证了转速的稳定性。此外，根据2种控制策略下不同风速时系统的控制器参数根轨迹、Nyquist曲线和Bode图，进一步验证了风力发电机控制器设计的稳定性，并分析了不同滤波时间常数对功率平滑效果的影响。

1 系统模型

1.1 风力机模型

风力机吸收的最大功率PW，opt可表示为：

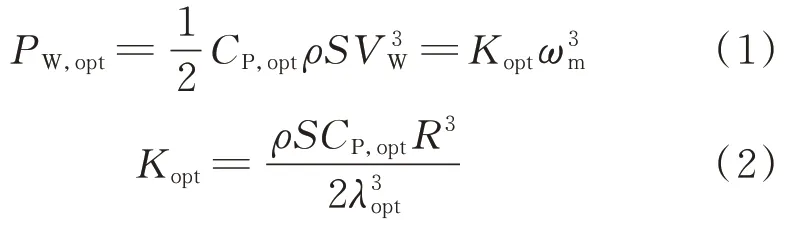
式中：S=πR2为风力机的扫描面积，其中，R为风力机的叶片半径；ρ为空气密度；VW为实际风速；ωm为风力机的旋转角速度；λopt为最佳叶尖速比；CP，opt为桨距角β=0时的最大风能利用系数。当β=0时，表征风力机吸收和利用外界风能效率高低的风能利用系数CP与叶尖速比λ之间的关系曲线如附录A图A1所示。

同时，风力机捕获的功率PW可以表示为：

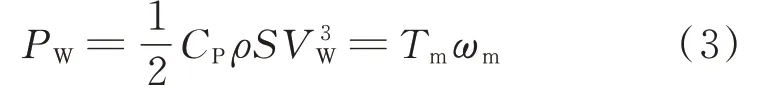
式中：Tm为输入风力机的转矩。

由式（3）可推出：

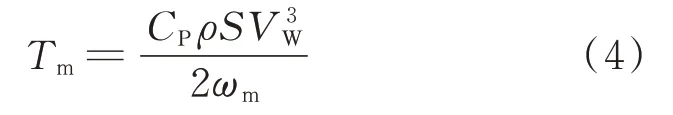
1.2 永磁同步发电机模型

永磁同步发电机（PMSG）在d-q旋转坐标系下的电压为：

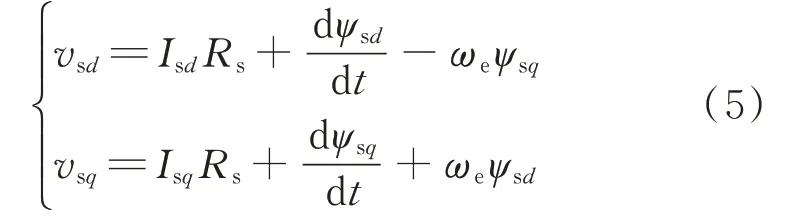
式中：vsd和vsq分别为PMSG的d轴和q轴电压分量；Isd和Isq分别为PMSG的d轴和q轴电流分量；ψsd和ψsq分别为d轴和q轴定子绕组磁链，具体见式（6）；Rs为定子的等效电阻；ωe=pωm为电角速度，其中，p为发电机极对数。

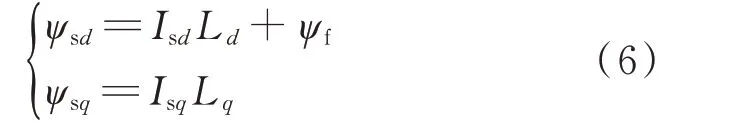
式中：Ld和Lq分别为d轴和q轴定子等效电感；ψf为永磁磁链。

PMSG的电磁转矩Te可表示为：

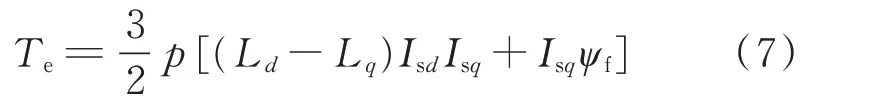
PMSG的运动方程为：

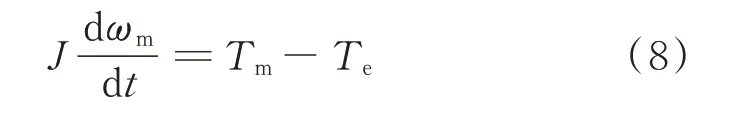
式中：J为转动惯量。由于直驱PMSG与风力机同轴相连，J可等效为风力机和PMSG的转动惯量之和。

2 风力机稳定性分析

2.1 传递函数的建立

在转速ωm下，风力机转子中储存的动能Em可以表示为：

当ωm变化时，风力机转子动能变化所提供的功率Pm可表示为：

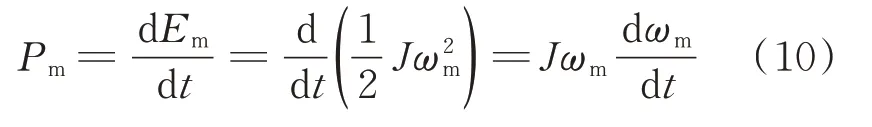
由上述方程可知，功率Pm不仅与转速ωm有关，还与速度变化率dωm/dt有关。因此，可根据风力发电机的输入功率PW、功率Pm和输出功率Pe间的基本关系调节dωm/dt来平衡功率，具体表达式为：

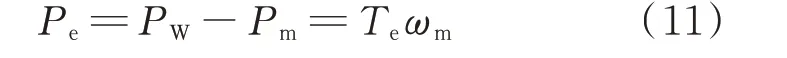
附录A图A2表示的是风速、转速变化时风力发电机的输入功率PW的变化曲线，图中给出了高、中、低3组不同风速。

在稳定运行状态下，风力机按照MPPT曲线（即附录A图A2中虚线）运行以便最大程度地吸收风能。风速在9 m/s和12 m/s之间发生突变时，风力机获得的功率PW将随着曲线ABC增加，然后随曲线CDA减少（图A2中橙色箭头）。然而，此时功率变化得很快，甚至在风速降低时会发生过冲，导致并网系统不希望发生的大功率波动。因此，为了获得更平滑的功率，可使功率变化遵循曲线AB′C和CD′A（即图A2中紫色箭头），以转子动能变化所提供 的功率Pm来补偿区域ABCB′、CDAD′内功率的差异。Pm由控制器间接调节，因此重要的是对控制器进行优化设计，并需考虑风力机运行的稳定性，具体分析如下。

首先，建立风力发电机从风速到输出功率、转速、转矩的无量纲传递函数GP/V(s)、Gω/V(s)、GT/V(s)［22-23］：

考虑风力发电机的2种典型功率平滑控制策略，即改进MPPT控制和功率反馈控制，分别建立这2种控制策略下从风速到输出功率、电磁转矩和转速的传递函数，在频域上设计控制器的优化控制参数。图1为2种控制策略下转速与输出功率的关系图。

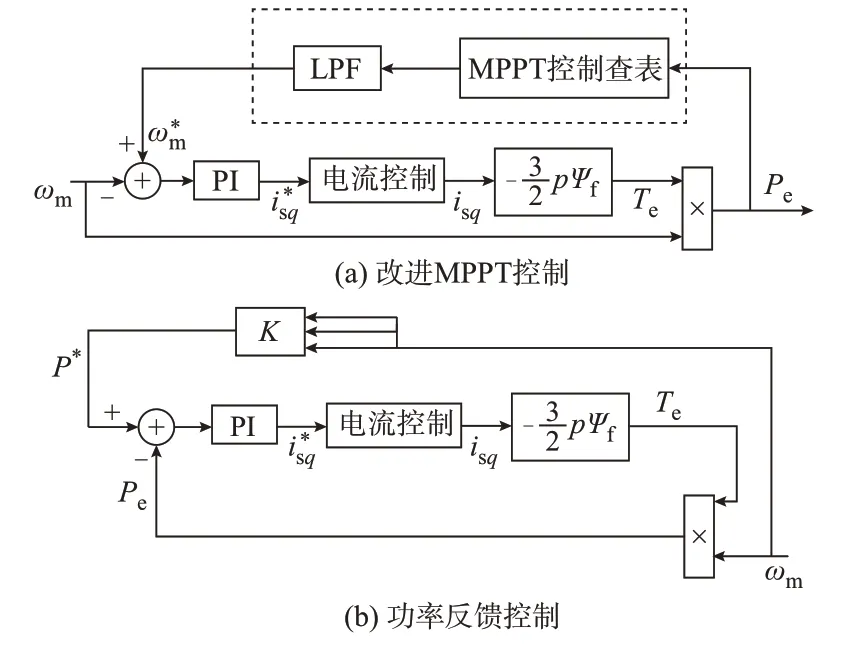
图1 转速与功率的关系Fig.1 Relationship between rotational speed and power

2.1.1改进MPPT控制下的传递函数

MPPT控制下，风力发电机的输出功率会自动跟踪并稳定在下一个风速的最大功率点处。由于风电系统较大转动惯量的作用，风速变化时系统转速不会发生突变，并利用风力机转子来储存动能，该动能可用来平衡功率。因而MPPT控制具有一定程度的功率平滑能力。改进MPPT控制在其基础上引入低通滤波器（LPF），可将大于截止频率的高频输出信号剔除，以进一步增强系统对更低频段的功率波动的平滑作用。改进MPPT控制可进一步利用系统的转动惯量，保证其对有功功率波动更好平滑效果的同时，避免功率输出信号的振荡。

根据上述发电机模型以及转矩方程式，转速ωm与风力发电机的输出功率Pe间的关系如图1（a）所示，附录B图B1是基于滞环矢量控制的PMSG控制框图。图中：ω*m为转速的参考值，可通过查找Pe与ωm之间的关系曲线得到。MPPT控制中LPF的传递函数可表示为：

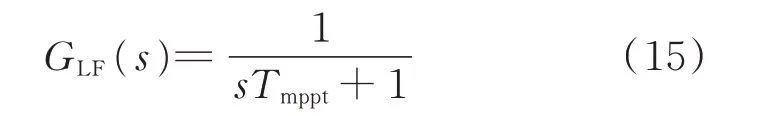
式中：Tmppt为LPF的滤波时间常数。

定义变量slope为：

根据图1（a）的MPPT控制框图，可得转速参考值为：

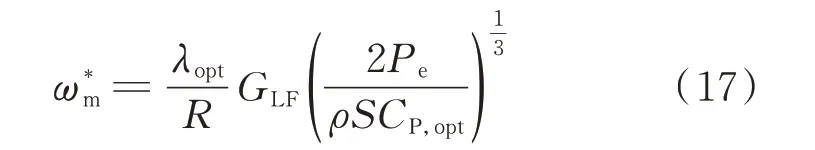
由附录B式（B1）—式（B7）可推出：

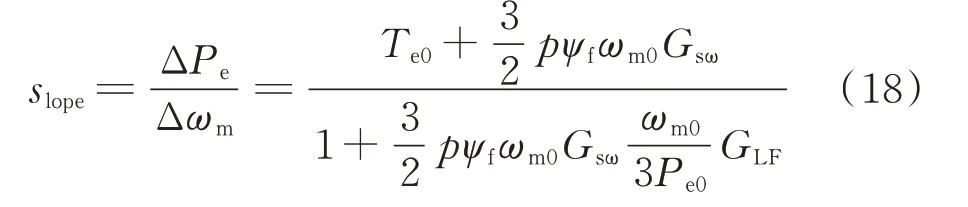
风力发电机转速环的比例-积分（PI）控制器的传递函数Gsω可表示为：

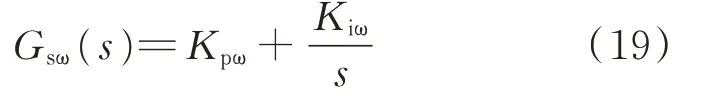
式中：Kpω和Kiω分别为PI控制器的比例系数和积分系数。

由附录B式（B11）可知，从风速到输出功率的无量纲传递函数实际上是3阶的，为将其简化为2阶，考虑

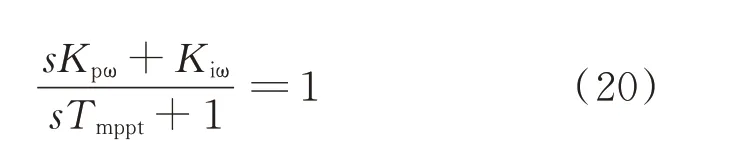
即令控制器的参数满足Kpω=TmpptKiω。当式（20）不满足时，3个3阶传递函数的表达式如附录B式（B12）—式（B15）所示。此时，可令控制器的参数满足Kpω=TPIKiω，其中，TPI为某一常数值。

当降阶条件式（20）满足时，将式（18）、式（20）代入附录B式（B8）—式（B10）中，可得改进MPPT控制下从风速到输出功率、转速、转矩的传递函数，具体表达式如下。

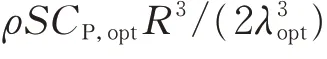
2.1.2功率反馈控制下的传递函数

根据上述风力发电机模型以及转矩方程，考虑风力发电机的功率反馈控制策略，以风力机捕获的最大风能作为功率参考值，转速ωm和风力发电机输出功率值Pe间的关系如图1（b）所示，附录C图C1是基于滞环矢量控制的完整框图。图中：P*为风力机输出功率的参考值，通过风力机的最大跟踪功率PW，opt得到，参数K根据实际需求选择，在MPPT控制下取Kopt。控制器的传递函数表达式同2.1.1节式（19）。

当风力发电机以MPPT的工况运行时，其无法预留有功备用，在电网频率跌落发生时，将不能提供有功支撑。因此，风力机往往通过减载控制放弃风能的最大捕获，使风力机保持一定的备用容量［26］。低风速段通常使用风力机在MPPT区域的超速减载控制来获取备用。

考虑一定减载率下的功率反馈控制，风力机所获得的最大风能为PW，opt，d，图1（b）中K值取Kd，具体表达式如下。

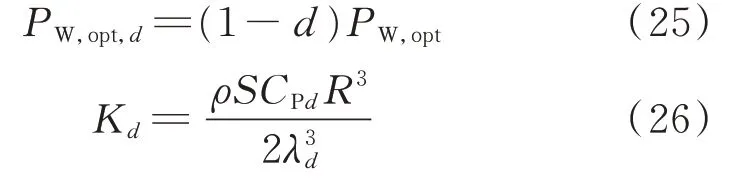
式中：d为减载率，一般取小于1的值；CPd和λd分别为减载率取d时风力机的风能利用系数和叶尖速比，可由式（27）和式（28）求得。

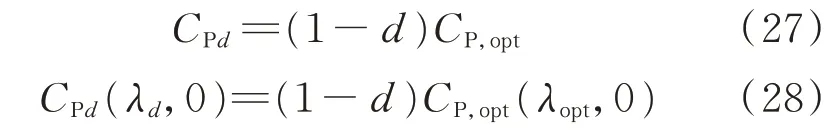
推导功率反馈控制下的传递函数，根据图1（b）的功率反馈控制框图可得：

由附录C式（C1）—式（C5）可得：

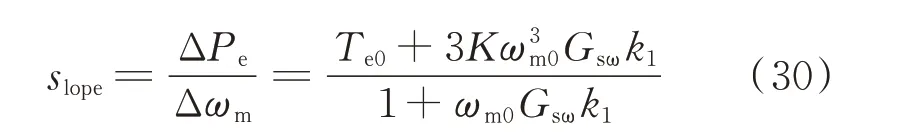
另外，为了简化从风速到输出功率的无量纲传递函数的计算，考虑

式中：T为某一固定正值。

将slope的推导式（30）及简化条件式（31）代入附录B式（B8）—式（B10），可得功率反馈控制下从风速到输出功率、转速、转矩的传递函数表达式如下。

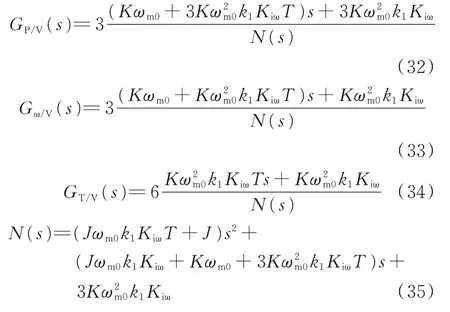
2.2 风力机运行稳定性分析

为了使功率得到最大限度的平滑，应尽可能减小GP/V(s)的带宽，而前提是必须始终将风力机保持在稳定的区域。附录D图D1（a）表示机械转矩与转速的函数关系。曲线L由每个风速下的最大转矩点组成。曲线L的右侧称为稳定区域（dTm/dt＜0），所以风力机的运动将被阻尼；曲线L的左侧称为不稳定区域（dTm/dt＞0），因此，风力机的运动将得到增强。若风力机位于不稳定区域且dωm/dt＞0，则其将加速进入稳定区域。但是，若风力机处于不稳定区域且dωm/dt＜0，则其将减速直到停止，除非风速低于切入风速，否则这是不期望发生的［23］。

在MPPT控制下，风力机的静态运行点均处于稳定区域。但在稳定区域中，若风速下降（下降量为ΔVW）时，转 速 会 下 降（下 降 量 为 Δω1）即dωm/dt＜0，且有一个超调Δωos响应，风力机有可能进入不稳定区域。转速的运动由Δω1和Δωos组成，如附录D图D1（b）所示。超调Δωos可以是正的，但应小于MPPT曲线和曲线L之间的间隙，以免风力机意外停机。

2.2.1基于传递函数的稳定约束条件

对于传递函数GP/V(s)、Gω/V(s)、GT/V(s)，令s=jω，可 得 频 域 下 的 频 率 特 性GP/V(jω)、Gω/V(jω)、GT/V(jω)。接下来将基于传递函数的频率特性分析稳定约束条件。

由于在风速大幅降低的情况下存在Δωos≪Δω1，因此，对风力机稳定性的约束可由式（36）表示，即在MPPT的稳态运行状态下，风速与转速之比固定。

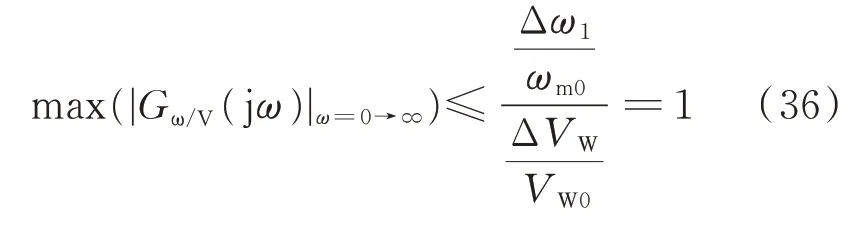
由式（22）和式（33）可得，改进MPPT控制及功率反馈控制下存在：

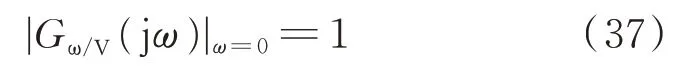
因此，若要有效地确保风力机的稳定和正常运行，需|Gω/V（jω）|≤1。同时，将GP/V(jω)、Gω/V(jω)和GT/V(jω)的超调量MP、Mω、MT定义为：

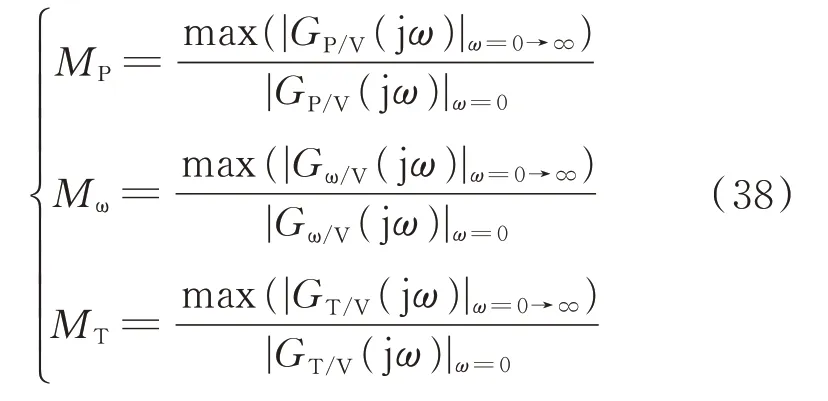
故对风力机稳定性的约束可表示为：

2.2.2基于特征根的稳定约束条件

由传递函数表达式（21）—式（24）可知，该改进MPPT控制下的特征根方程表示为：

由传递函数表达式（32）—式（35）可知，该功率反馈控制下的特征根方程可表示为：

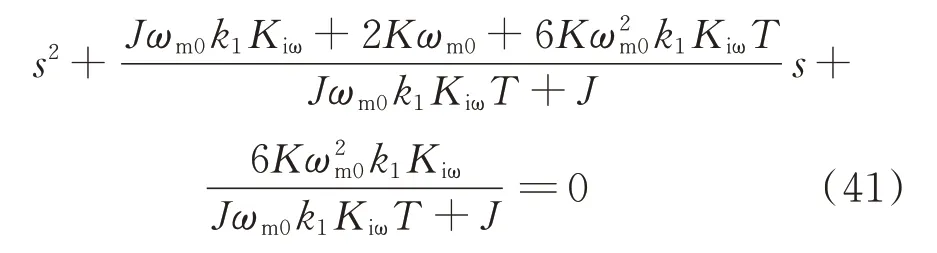
特征根的位置可以反映稳定性，当所有特征根的实部均为负时，表明系统是稳定的。为保证系统稳定，同时增大振荡阻尼、减少振荡周期数，控制器参数的选取应使得特征根的实部全为负且尽可能保证实部绝对值较大、虚部绝对值较小［27］。

3 控制器的优化设计及稳定性验证

3.1 控制器的优化参数设计

将式（21）—式（24）、式（32）—式（35）分别代入式（38）可得2种控制下各传递函数的最大幅度即超调 量MP、Mω、MT的 计 算 公 式。选 取 低、中、高（6 m/s、9 m/s、12 m/s）3组风速，分别绘制不同风速下各超调量随控制器参数Kiω变化的关系曲线。根据曲线选取控制器的优化设计参数值或范围，其中，时间常数Tmppt为1 s，风电系统的其他参数为：风力机 中，R=35 m，ρ=1.225 kg/m3，λopt=8.1，CP，opt=0.48，额 定 风 速VWN=12 m/s，额 定 功 率PN=2 MW；PMSG中，定子电阻为0.01Ω，电感为0.835 mH，J=128 500 kg·m2，ψf=8.76 Wb，极对数p=32。

3.1.1基于改进MPPT控制的参数设计

当满足降阶条件即Kpω=TmpptKiω时，超调量MP、Mω、MT随控制器参数Kiω的变化关系如图2所示，并取LPF的 时 间 常 数Tmppt=1 s。当Kiω减 小 时，带 宽减小，而GP/V(jω)、Gω/V(jω)和GT/V(jω)的超调值具有不同的变化趋势。基本上，GP/V(jω)、Gω/V(jω)的超调值将增加，而GT/V(jω)的超调值将减少。因此，当需要更平滑的输出功率时，需要更窄的带宽，但是同时将引入更大的转速变化。

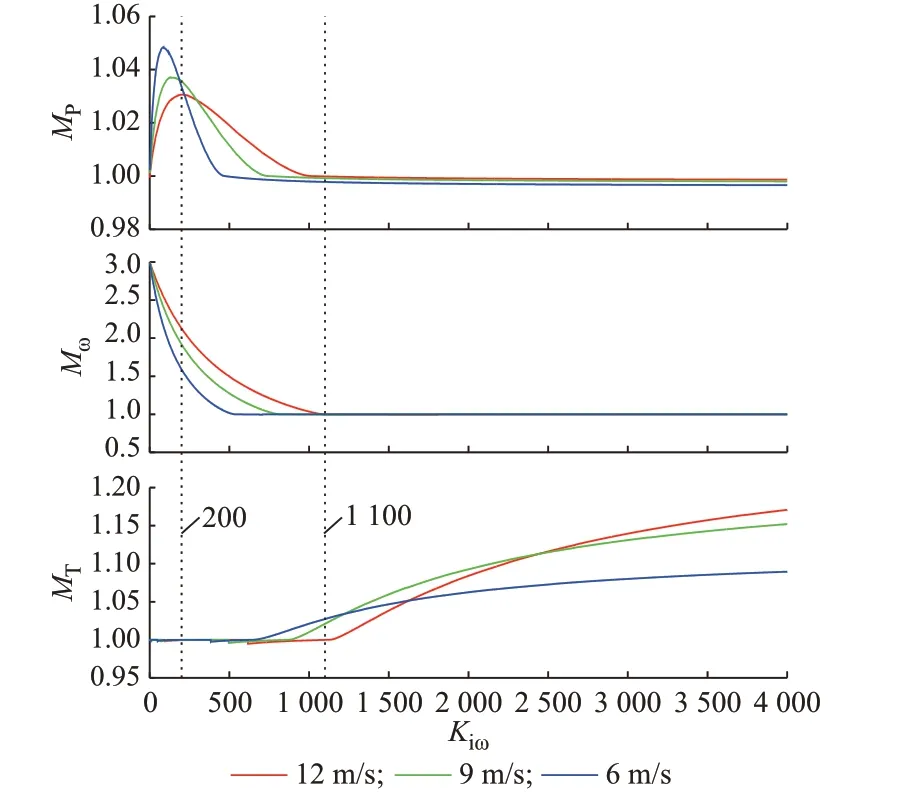
图2 改进MPPT控制下超调量MP、Mω、MT与控制器参数的关系Fig.2 Relationship between overshoot MP、Mω、MT and controller parameters with improved MPPT control

由图2的超调量关系曲线可以看出，Kiω取1 100左右是控制器参数在最佳取值区间的情况，此时获得了较小的GP/V(s)带宽，同时保证了较小的转矩谐振（振幅不超过1.03 p.u.），但仍满足风力机稳定运行的约束条件。位于Kiω=1 100左侧区域的风力机是不稳定的，转速超调量Mω＞1；右侧区域是稳定的，但是转矩的谐振振幅随着Kiω的增加而逐渐增大，故过大的Kiω也不是理想的控制器参数取值。因此，分别在过优设计、优化设计、欠优设计区间内选取3组参数，如表1所示。

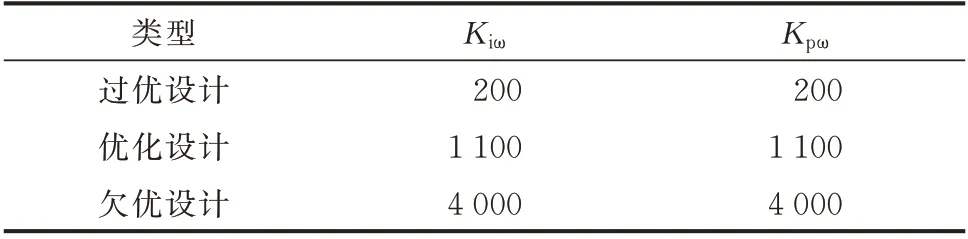
表1 PI控制器参数Table 1 Parameters of PI controller

3.1.2基于功率反馈控制的参数设计

在减载率d=20%的功率反馈控制下的超调量随控制器参数的变化关系如附录E图E1所示，并取控制器中Kpω与Kiω的倍数T=1。另外，根据附录C式（C6）和式（C7）可知，由于传递函数表达式里与变化 参 数有关的 变量R中ωm0k1的值较大，故Kiω取 值稍大时R值近似为1，各传递函数幅值波动变化较小。对 应 于 附 录E图E1，当Kiω变 化 时，GP/V(jω)、Gω/V(jω)和GT/V(jω)的超调值几乎保持不变。由图E1可得出结论：在当前系统参数取值下，无论控制器参数Kiω如何取值，风力机都是运行在稳定区间的，且均有着较小的GP/V(jω)带宽和较小的转矩振荡。

3.2 基于设计参数的稳定性验证

3.2.1变控制器参数的根轨迹

由2.2.2节所得的传递函数的特征根方程式（40）和式（41）绘制2种控制策略下控制器参数Kiω分别在1 000～4 000和1～1 000范围内变化时的根轨迹曲线及局部放大图如图3所示，灰色箭头方向为Kiω增大时的根轨迹走向。

根据特征根轨迹曲线图3（a）可看出，当风速分别为6、9、12 m/s（图3（a）中从上到下的根轨迹对应的风速分别为6、9、12 m/s），Kiω在1 000～4 000范围内变化时，根轨迹均位于坐标系左半平面，即所有特征根的实部均为负。因此可知控制器参数在该取值范围内时风力机是稳定的，所得结论与2.2.1节风力机稳定约束条件一致，即在优化设计区间及欠优设计区间内选取的控制器参数是满足稳定运行条件的。

同理，由根轨迹曲线及其局部放大图（图3（b））可知，当风速分别为6、9、12 m/s（图3（b）中从上到下的根轨迹对应的风速分别为6、9、12 m/s），Kiω在1～1 000范围内变化时，特征根均位于坐标系左半平面。因此，可知控制器参数在该取值范围内时风力机是稳定的，所得结论与由附录E图E1得出的结论一致。

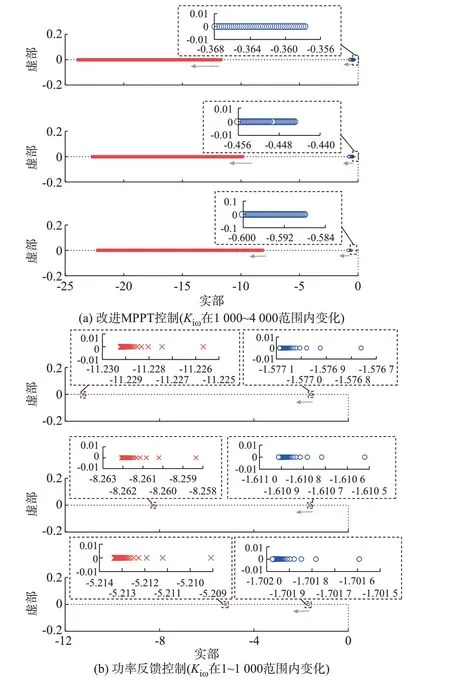
图3 不同风速的变控制器参数根轨迹Fig.3 Root locus of variable controller parameterswith different wind speed

3.2.2基于控制器参数的Nyquist曲线及Bode图

根据自动控制原理中Nyquist稳定判据可知，反馈控制系统稳定的充要条件是：Nyquist曲线逆时针包围(-1，j0)点的次数等于系统开环右极点的个数。接下来将通过不同控制器参数下的Nyquist曲线和Bode图即对数幅频特性、对数相频特性曲线来验证2种控制下风力机运行的稳定性及优化设计参数选取的合理性。

改进MPPT控制中，3种控制器参数下系统的各传递函数Nyquist曲线和对数幅频特性、对数相频特性如图4所示。

由图4可以看出，在欠优设计和优化设计下，Gω/V(s)都没有谐振，且满足了Nyquist稳定判据，但欠优设计中GP/V(s)的带宽要高于优化设计，且欠优设计中GT/V(s)存在一些很小的谐振。在过优设计中，虽然GT/V(s)几乎不存在谐振，且GP/V(s)的带宽小于优化设计，但其Gω/V(s)的谐振较大，与图2所得结果一致。而优化设计下，GT/V(s)和Gω/V(s)几乎不存在谐振，且GP/V(s)的带宽较小。因此，可知在优化设计参数及欠优设计参数下，风力机均能处于稳定运行状态，但优化参数下控制系统滤波的效果要优于欠优参数；而在过优设计参数下，控制系统虽然有着较好的滤波效果，但风力机不能稳定运行。

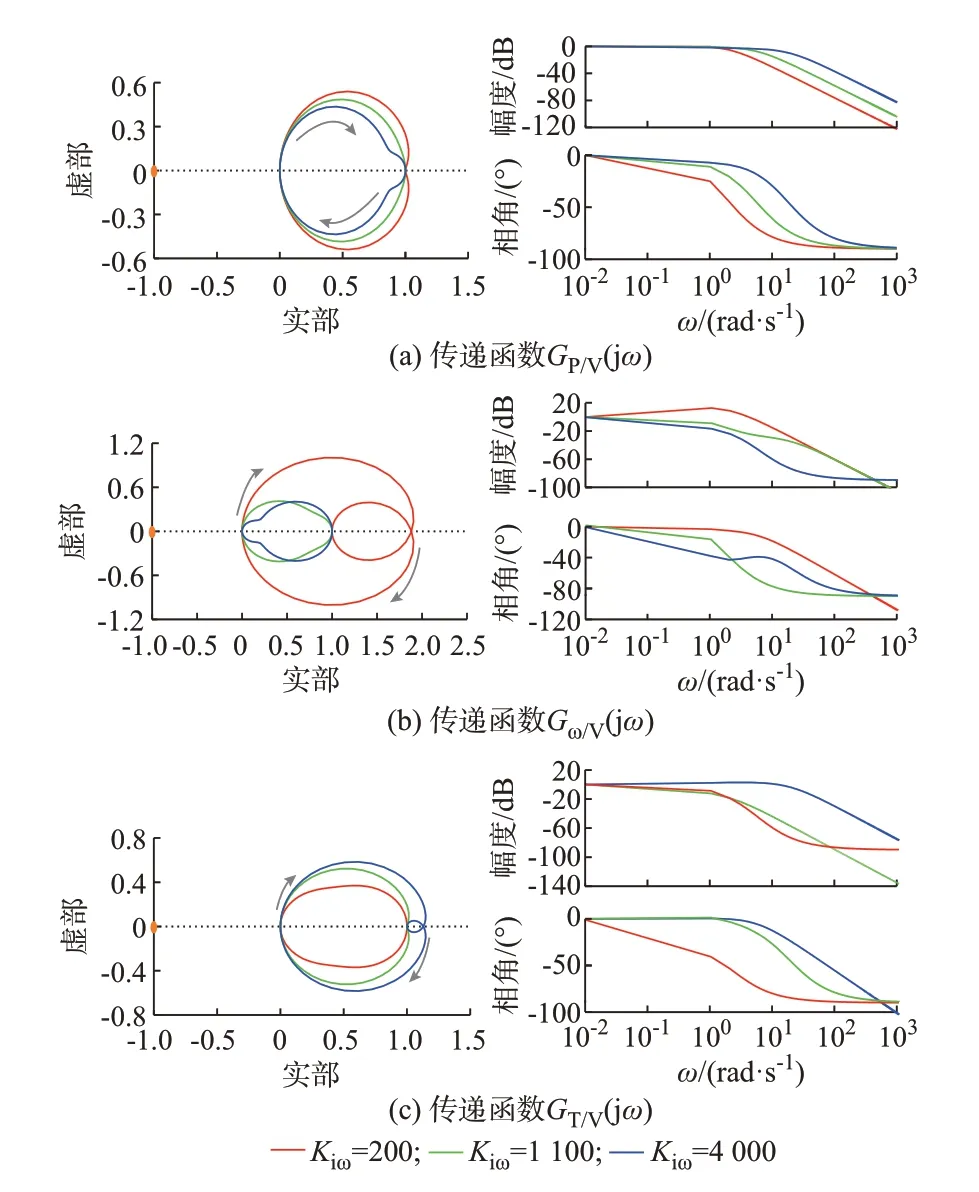
图4 不同参数下各传递函数的Nyquist曲线及Bode图Fig.4 Nyquist curves and Bode plots of various transfer functions with different parameters

基于前文提出的控制器参数优化方法，分别另选时间常数Tmppt为5 s和0.1 s，根据该参数下的传递函数超调量曲线，得出此时改进MPPT控制下优化设计的控制器参数。Tmppt取5 s时，控制器优化参数Kpω和Kiω分 别 取1 100和220；Tmppt取0.1 s时，控 制器 优 化 参 数Kpω和Kiω分 别 取770和7 700。接 下 来将分析不同滤波时间常数Tmppt对功率平滑效果的影响。控制器取优化参数时，3个传递函数GP/V（jω）、Gω/V（jω）和GT/V（jω）在不同时间常数下的对数幅频特性曲线见附录E图E2。

由附录E图E2可看出，在优化设计参数的取值下，GP/V（jω）、Gω/V（jω）和GT/V（jω）的幅度值均在0以下。另外，随着时间常数的降低，GP/V（jω）、Gω/V（jω）和GT/V（jω）的带宽会有所减小，但变化并不大，且功率与风速间的传递函数GP/V（jω）的带宽几乎是没有变化的，说明滤波时间常数的改变对功率平滑效果的影响较小。

在减载率d=20%的功率反馈控制中，基于3.1.2节的分析可知，不同控制器参数下各传递函数的频率特性几乎相同。故仅考虑控制器参数Kiω=100下3个传递函数的Nyquist曲线、对数幅频特性和对数相频特性曲线，见附录E图E3。由图E3可以看出，在该控制器参数下，GP/V（jω）、Gω/V（jω）和GT/V（jω）几乎都没有谐振，且满足Nyquist稳定判据，与图E1和图3（b）所得结果一致。

4 仿真验证

在MATLAB/Simulink中建立了永磁同步风电系统仿真模型，验证第3章所提出的基于功率平滑的控制器优化参数设计方法的有效性和可行性。风力机和PMSG的参数同3.1节，转动惯量是风力机和PMSG两者的总和。直流侧参考电压设为2 000 V，无功功率参考值设为0。

4.1 改进MPPT控制策略下的仿真

4.1.1满足传递函数降阶条件时的仿真

基于改进MPPT控制策略，当Tmppt=1 s、Kpω=TmpptKiω且其余仿真参数相同时，分别对比了过优设计、优化设计、欠优设计3种不同水平的控制器参数下输出功率跟踪及平滑的效果。仿真所得的风力机输出功率如图5所示。控制器参数取值依次为200、1 100、4 000。优化设计、欠优设计下输出功率对比及局部放大图见图5（d）。Kiω取200、1 100、4 000时的转速和电磁转矩变化波形见附录F图F1。

由图5可看出，在过优设计的控制器参数下，虽然风力发电机能很好且快速地跟踪上最大功率点，并且具有一定的平滑效果，但在仿真进行到12 s左右时，风力机会失去稳定。在优化设计的控制器参数下，风力发电机能跟踪最大功率点，且随着仿真的进行风力机也不会失稳。同样地，在欠优设计的控制器参数下，风力发电机也可以跟踪最大功率点，且风力机也不会失稳。但由图5（d）可知，与优化设计参数下的结果相比，欠优设计下的平滑效果要稍差于前者，且效率也略低。综合来看，优化设计参数的选取可使风力机在保证稳定运行的同时，达到较好的功率跟踪、平滑效果。

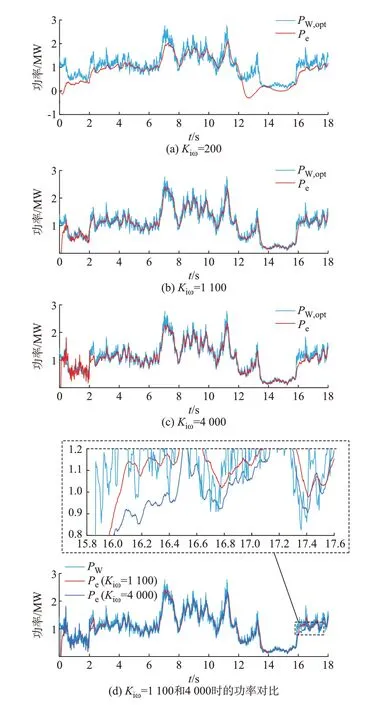
图5 改进MPPT控制下不同Kiω取值的输出功率波形Fig.5 Output power waveforms with different values of Kiωand improved MPPT control

由附录F图F1的转速波形可看出，在优化和欠优设计的控制器参数下，实际转速值可较好地跟踪参考转速，且优化设计下跟踪效果更好；而在过优设计下，实际转速波动较大，且仿真在12 s左右时实际转速由30 r/min跌落至-30 r/min，风力机失去稳定。

4.1.2不满足传递函数降阶条件时的仿真

当Kpω=TPIKiω时，超 调 量MP、Mω、MT随 控 制器 参 数Kiω的 变 化 关 系 如 附 录F图F2所 示，并 取LPF的 时 间常数Tmppt=5 s，TPI=1。由图F2可 看出，Kiω取2 000左右是控制器参数值在最佳取值区间的情况，此时转矩的谐振相对较大（小于1.3 p.u.），GP/V(jω)的谐振和带宽均较小（振幅约1.03 p.u.），转速超调值小于1，仍满足风力发电机稳定运行的约束条件。故而在优化设计区间内取控制器参数Kpω=Kiω=2 000。

基于改进MPPT控制策略，在其余仿真参数相同时，对比过优设计（Kiω=100）、优化设计（Kiω=2 000）、欠优设计（Kiω=5 600）这3种不同控制器参数下输出功率跟踪及平滑的效果，如附录F图F3所示。由图F3可以看出，在Kiω=2 000时的输出功率的平滑效果较好；实际转速能很好地跟踪参考转速并保持稳定，电磁转矩的波动也在可接受范围内。

4.2 功率反馈控制策略下的仿真

基于功率反馈控制策略，结合优化参数设计的分析，在其余仿真参数相同时，首先分析了没有减载即风力机运行在MPPT状态以及减载率为20%、50%时的输出功率，如附录F图F4所示。然后，对于减载20%的功率反馈控制做了进一步仿真，比较了控制器参数取值依次为1、10、100、1 000这4种不同情况下的输出功率跟踪及平滑的效果。仿真所得的风力发电机输出功率如图F5所示。Kiω=100时，未减载和减载20%、50%下的转速和电磁转矩变化波形如图F6所示。

由附录F图F4可以看出，在风力机减载运行后，反馈控制输出的功率值会随着减载率的变化而变化。由图F6可以看出，随着减载率的提高，实际转速值会相对提高，电磁转矩值会相对降低。由图F5可以看出，减载20%时，在这4种控制器的设计参数下，风力机都没有失稳且都能很好地快速跟踪最大功率，3.1.2节所研究分析的结论得以验证。

5 结语

本文建立从风速到输出功率、电磁转矩和转速的传递函数，在此基础上合理设计了风力发电机的2种控制策略——改进MPPT控制及功率反馈控制下用于功率平滑的控制器的参数优化取值。此外，分析了风力机基于传递函数和特征根方程的稳定运行约束条件，并通过研究控制器参数变化下的根轨迹曲线，验证了在该优化参数下风力机的运行是稳定的；通过研究不同设计水平控制器参数下的Nyquist曲线和Bode图，验证了优化参数下风力发电机功率跟踪和平滑效果较好。控制参数设计下的系统稳定性在仿真中得到了进一步的验证，优化设计区间内的参数可使风力发电机更好地追踪功率，且在使功率和转矩更加平滑的同时，风力机仍能处于稳定运行区域内。

本文在进行参数优化设计及验证时，只研究了基于滞环矢量控制的传递函数和单个控制器参数的设计，没有进一步研究基于空间矢量脉宽调制（SVPWM）的多个控制参数的优化。因此，下一步研究应考虑推导SVPWM下风力发电机控制策略的频域传递函数，并分析风力机运行稳定条件，研究多个控制器间的相互影响，对多控制参数进行合理的优化设计。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。