三叉式-球笼式双联万向联轴器的扭转振动特性分析

魏建宝，李松梅，徐雨田

（青岛科技大学机电工程学院，山东青岛266061）

万向联轴器作为大型旋转机械传动系统的重要组成部分，其力学性能对机械设备的稳定、安全运行有重要影响。三叉式万向联轴器具有结构简单、传输能力强和承载能力大等优点，广泛应用于汽车工业和冶金行业等［1-3］，其结构如图1所示。万向联轴器的主要运动形式是转动。在自身结构和外力的影响下，万向联轴器会产生附加运动，从而导致联轴器产生一定的振动，这会对机械设备传动系统的平稳运行造成极大的危害。

图1 三叉式万向联轴器结构示意Fig.1 Structure diagram of tripod universal coupling

近年来，许多学者对万向联轴器的振动特性进行了大量研究。Farzad 等［4］对万向联轴器的驱动轴进行了多体动力学分析，建立了万向联轴器的扭转振动方程并分析了振动产生的原因，最后通过实验进行了对比验证。Han等［5］通过研究发现，船舶传动系统的疲劳失效主要是由万向联轴器的扭转振动造成的，为避免传动系统疲劳失效，应将万向联轴器的刚度减小至目标值的70%。Jayananthan 等［6］对动力传动系统的扭转振动特性进行了建模分析，通过研究发现防止由临界速度下的共振引发的过早失效十分有必要。Sugawara等［7］考虑汽车传统系统驱动轴的轴向力，通过实验分析了驱动轴空转时的振动特性，发现驱动轴空转时的振动特性受到三脚架轴向位置变化幅度和谐波周期的影响。卢曦等［8］从球笼式等速万向节的内部结构出发，对其振动的产生原因进行了分析，并推导出球笼式等速万向节传动轴的弯曲、扭转振动方程以及对应的临界转速。常德功等［9-10］设计了一种汽车用新型等速万向联轴器，通过运动学分析验证了其准等角速特性，并对所设计的万向联轴器的驱动轴进行了预应力作用下的谐响应分析，得到了驱动轴的危险频率及动态特性，有效避免了共振现象的出现。徐翔等［11］通过更改参数的方式得到：三叉式万向联轴器的固有频率随其输入轴与输出轴之间夹角的增大而逐渐减小，当夹角小于20°时，可忽略夹角的影响，直接进行扭振特性分析。王鸿恩等［12］采用渐近法分析了三维空间多节万向传动轴的结构参数以及扭振的主、从动件的旋转非等速性等因素对动力放大系数的影响，提出可通过对传动件刚度、转动惯量、轴间夹角及十字轴转角相位差等进行优化设计的方法来减小动力放大系数和降低旋转的非等速性。袁跃兰等［13］建立了某车辆动力传动系统的多自由度质量-弹性-阻尼动力学模型，着重分析了万向联轴器的刚度和阻尼对车辆动力传动系统的固有频率、固有振型和强迫振动响应等模态参数的影响。李松梅等［14］针对三叉式万向联轴器在实际应用中所产生的振动影响，设计了一种橡胶减振型三叉式万向联轴器，并通过理论分析和实验研究的方式获得了提高其使用寿命的措施。综上所述，目前缺乏对双联万向联轴器扭转振动特性的研究。考虑到在实际应用中三叉式万向联轴器常与球笼式万向联轴器串联使用，且其扭转振动会对机械传动系统产生影响，以三叉式-球笼式双联万向联轴器为研究对象，对其扭转振动特性进行分析，旨在为其设计、制造和应用提供理论依据。

1 三叉式-球笼式双联万向联轴器的扭转振动模型的建立

三叉式-球笼式双联万向联轴器的物理模型如图2所示（其中三叉式万向联轴器为橡胶减振型三叉式万向联轴器）。图中：R为三叉杆的旋转半径；β为输入轴与中间轴的夹角；l为中间轴的长度；θ1、θ2及θ3和θ4分别为输入轴、中间轴和输出轴的扭转角度。忽略新型三叉式万向联轴器和球笼式万向联轴器自身的转动惯量，且不考虑连接处附加转动惯量和速度的变化，采用集中参数法建立三叉式-球笼式双联万向联轴器的扭转振动简化模型，如图3所示。其中：中间轴为细长轴（扭转刚度为kL，扭转阻尼为cL），其扭转变形量较大，分析计算时将中间轴分解为转动惯量相等的2个圆盘，对应的转动惯量分别为J2和J3；输入轴的转动惯量为J1，输出轴的转动惯量为J4。

图2 三叉式-球笼式双联万向联轴器的物理模型Fig.2 Physical model of tripod-ball cage double univer‐sal coupling

图3 三叉式-球笼式双联万向联轴器的扭转振动简化模型Fig.3 Simplified torsional vibration model of tripodball cage double universal coupling

基于图3所示的扭转振动简化模型，采用第一类拉格朗日方程［15］建立三叉式-球笼式双联万向联轴器的动力学方程：

式中：M为广义质量矩阵，M=diag(J1J2J3J4)；q为广义坐标，q=[θ1θ2θ3θ4]T；Cq为雅克比矩阵；λ为拉格朗日乘子；Qe为阻尼矩阵；Qf为外力矩阵。

由图2 可知，三叉式-球笼式双联万向联轴器输入轴、中间轴与输出轴的扭转角度的关系为：

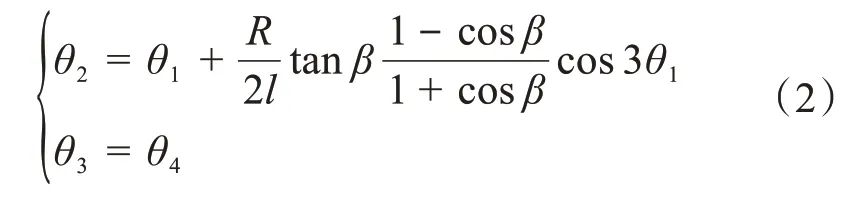
则三叉式-球笼式双联万向联轴器各轴扭转角度的约束矩阵C为：

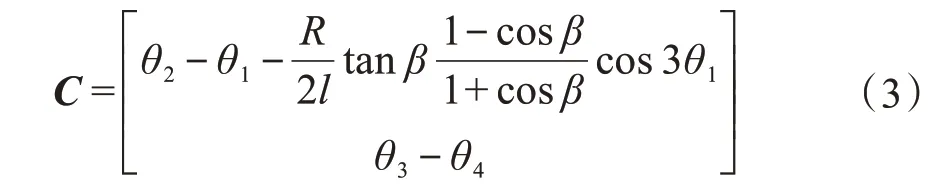
求解式（3）关于广义坐标q的偏导数，可得Cq：

根据图3所示的扭转振动简化模型，可得阻尼矩阵Qe为：

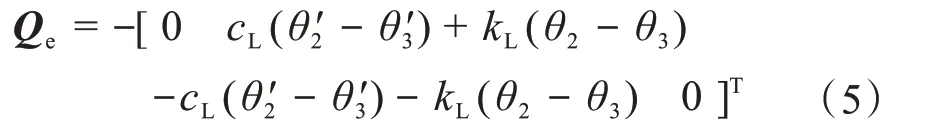
求解式（2）关于时间的二阶导数，可得Cqq''=Qc，则有：

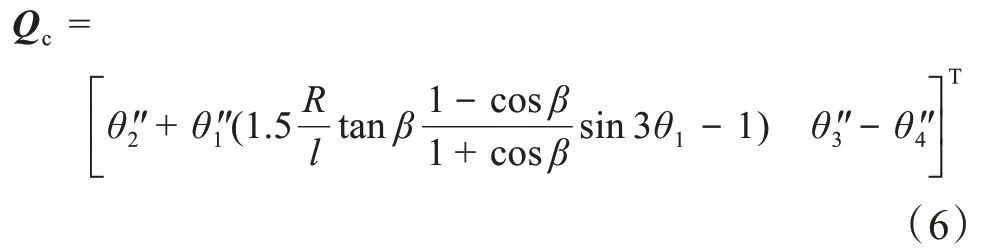
将Cqq''=Qc代入式（1），可得：

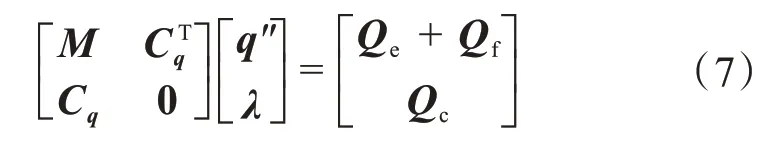
当外力为0 N 时，阻尼为0 N/（m/s）时，式（7）为三叉式-球笼式双联万向联轴器的自由扭转振动方程。令β=0°，则θ1=θ2，θ3=θ4，由此可得角加速度也相等。此时该双联万向联轴器的自由扭转振动方程可以简化为：

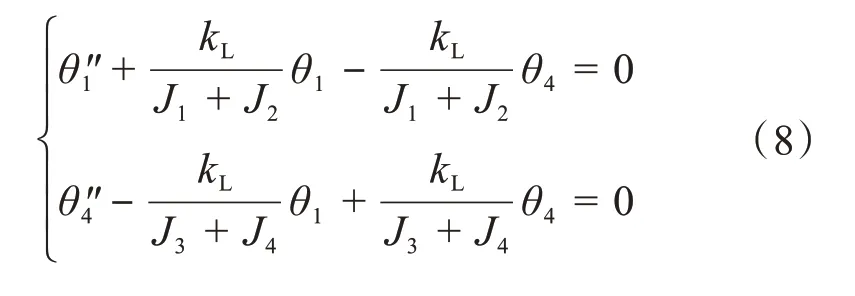
2 三叉式-球笼式双联万向联轴器的固有频率求解

基于式（8），由公式法［16］求解得到三叉式-球笼式双联万向联轴器的固有频率fn：

三叉式-球笼式双联万向联轴器各轴的转动惯量分别为J1=J4=4×10-3kg⋅m2，J2=J3=9×10-3kg⋅m2；双联万向联轴器的剪切模量G=8×1010Pa；中间轴的直径d=0.04 m，长度l=0.40 m；三叉杆的旋转半径R=0.03 m。则可得中间轴的扭转刚度kL为：

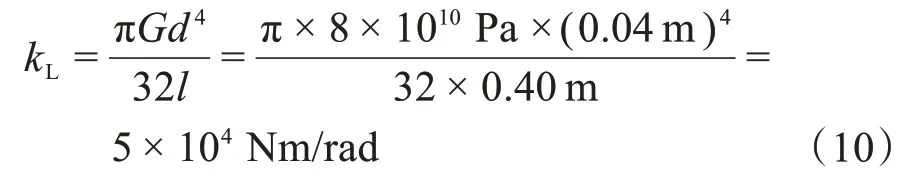
将各数值代入式（9），可得三叉式-球笼式双联万向联轴器的固有频率为2 769.4 rad/s，即440.99 Hz。

若三叉式-球笼式双联万向联轴器输入轴与中间轴的夹角β≠0°，保持输入轴与输出轴的轴线平行，则基于式（7）得到该双联万向联轴器的振动方程，为：

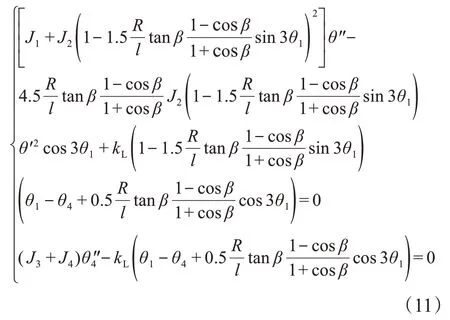
式（11）为非线性振动方程，利用公式法求解较为复杂且误差较大，因此采用Runge-Kutta 算法对式（11）进行数值求解。设三叉式-球笼式双联万向联轴器输入轴的初始角速度为1 rad/s，分析时间为1 s，步长为10-6s；取输入轴与中间轴的夹角β=0°，10°，20°和30°。利用MATLAB 软件对三叉式-球笼式双联万向联轴器的振动特性进行仿真分析。

图4所示为输入轴与中间轴的夹角不同时三叉式-球笼式双联万向联轴器的频域响应。由图4 可知，当输入轴与中间轴的夹角β=0°时，该双联万向联轴器的固有频率为440.99 Hz，与理论计算结果一致，验证了仿真分析的正确性。此外，从图4中还可以看出，随着输入轴与中间轴的夹角的增大，三叉式-球笼式双联万向联轴器的固有频率略有降低。

图4 输入轴与中间轴的夹角不同时三叉式‑球笼式双联万向联轴器的频域响应Fig.4 Frequency domain response of tripod-ball cage double universal coupling with different included angles be‐tween input shaft and intermediate shaft

3 三叉式-球笼式双联万向联轴器的扭转振动响应分析

在考虑外力且忽略阻尼的情况下，在三叉式-球笼式双联万向联轴器的输入轴上加载转矩T，输出轴上施加负载F，则有：

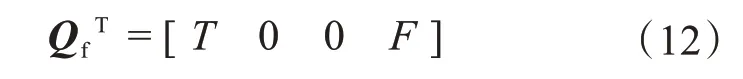
将Qf代入式（7），得到三叉式-球笼式双联万向联轴器的扭转振动方程，为：

设施加在三叉式-球笼式双联万向联轴器输入轴上的转矩T=sin 8πtN∙mm，不考虑该双联万向联轴器的效率损失，利用Runge-Kutta算法对式（13）进行数值求解，得到该双联万向联轴器输入轴与输出轴之间的转角差和角速度差随时间的变化情况。

3.1 不同夹角下的扭转振动响应分析

在实际应用中，三叉式-球笼式双联万向联轴器输入轴与中间轴的夹角会发生改变。为研究该双联万向联轴器输入轴与输出轴的转角和角速度与输入轴与中间轴的夹角的关系，设输入轴和输出轴的初始角速度均为1 rad/s，保持输入轴与输出轴的轴线平行，取输入轴与中间轴的夹角β=0°，10°，20°和30°，负载F=sin 8πtN∙mm，分析时间为1 s。通过仿真分析得到不同夹角下三叉式-球笼式双联万向联轴器输入轴与输出轴之间的转角差和角速度差随时间的变化情况，如图5所示。

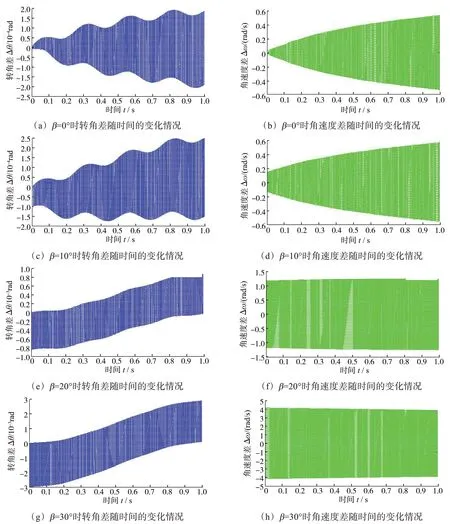
图5 不同夹角下三叉式-球笼式双联万向联轴器输入轴与输出轴之间的转角差和角速度差Fig.5 Rotation angle difference and angular velocity difference between input shaft and output shaft of tripod-ball cage double uni‐versal coupling under different included angles

由图5 可知，对于三叉式-球笼式双联万向联轴器，当输入轴与中间轴的夹角β=0°时，随着时间的增加，其输入轴与输出轴之间的转角差逐渐增大，呈波浪形，角速度差平稳增大。当输入轴与中间轴的夹角β=10°时，输入轴与输出轴之间的转角差和角速度差的整体变化趋势与β=0°时相似，但波动幅度增大。当输入轴与中间轴的夹角β=20°时，随着时间的增加，输入轴与输出轴之间的转角差和角速度差整体趋于稳定，转角差的最大值约为0.8×10-3rad，角速度差的最大值约为1.3 rad/s。当输入轴与中间轴的夹角β=30°时，输入轴与输出轴之间的转角差和角速度差的变化趋势与β=20°时相似，其中转角差的最大值约为3×10-3rad，角速度差的最大值约为4.1 rad/s，随着时间的增加，角速度差略有减小。

由图5还可以看出，对于三叉式-球笼式双联万向联轴器，随着输入轴与中间轴的夹角β的不断增大，同一时刻下输入轴与输出轴之间的转角差增大。从整体上看，在t=0 s附近，随着输入轴与中间轴的夹角β的增大，输入轴与输出轴之间的转角差和角速度差的初始值增大；当输入轴与中间轴的夹角β较小时，输入轴与输出轴之间的转角差整体呈波浪形变化，变化趋势不稳定；当输入轴与中间轴的夹角β增大到20°后，输入轴与输出轴之间的转角差的整体变化趋势由波浪形趋于平滑，即变化逐渐趋于稳定；随着输入轴与中间轴的夹角β的增大，输入轴与输出轴之间的角速度差增大，且在t=0 s附近的角速度差随夹角β的增大而快速增大，逐渐接近t=1 s时的角速度差。

综上，三叉式-球笼式双联万向联轴器输入轴与中间轴的夹角的改变导致其输入轴与输出轴之间的转角差和角速度差发生改变，从而造成联轴器产生不稳定的扭转振动。

3.2 不同外激励下的扭转振动响应分析

为研究三叉式-球笼式双联万向联轴器输入轴与输出轴的转角和角速度与外激励的关系，分别取施加在输入轴上的转矩T=30sin 8πt，60sin 8πt和90sin 8πtN∙mm，输出轴外激励为相应的负值，取输入轴与中间轴的夹角β=10°，输入轴和输出轴的初始角速度均为1 rad/s，其他条件不变，得到输入轴与输出轴之间的转角差和角速度差随时间的变化情况，如图6所示。

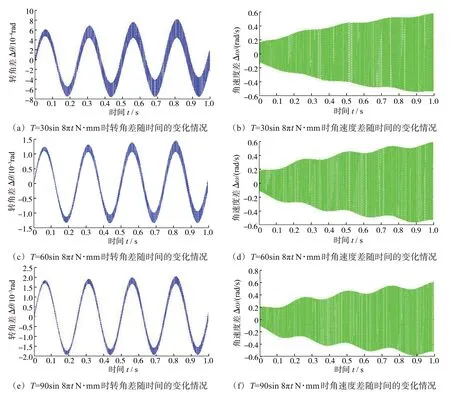
图6 不同外激励下三叉式-球笼式双联万向联轴器输入轴与输出轴之间的转角差和角速度差Fig.6 Rotation angle difference and angular velocity difference between input shaft and output shaft of tripod-ball cage double uni‐versal coupling under different external incentives

由图6（a）、（b）可以看出，对于三叉式-球笼式双联万向联轴器，当外激励T=30sin 8πtN∙mm时，输入轴与输出轴之间的转角差整体呈周期性变化，变化周期约为0.25 s，正、反向转角差的最大值随时间的增加而增大，正向转角差的最大值约为8×10-4rad，反向转角差的最大值约为-8×10-4rad；输入轴与输出轴之间的角速度差在0 rad/s上下波动，且随着时间的增加，角速度差呈小波浪形增大，正向角速度差的最大值约为0.60 rad/s，反向角速度差的最大值为-0.55 rad/s。由图6（c）、（d）可以看出，当外激励T=60sin 8πtN∙mm时，输入轴与输出轴之间的转角差的变化趋势以及变化周期与T=30sin 8πtN∙mm时相似，正向转角差的最大值约为1.8×10-3rad，反向转角差的最大值约为-1.8×10-3rad；输入轴与输出轴之间的角速度差的变化趋势也与T=30sin 8πtN∙mm时相似，但波动程度有所增大。由图6（e）、（f）可以看出，当外激励T=90sin 8πtN∙mm 时，输入轴与输出轴之间的转角差的变化趋势以及变化周期同样与T=30sin 8πtN∙mm时相似，正向转角差的最大值约为2.0×10-3rad，反向转角差的最大值约为-2.0×10-3rad；输入轴与输出轴之间的角速度差的变化趋势同样与T=30sin 8πtN∙mm时相似，且正、反向角速度差的最大值与T=30sin 8πtN∙mm时相近，但角速度差的波动程度略有增大。

综上，外激励的存在和改变导致三叉式-球笼式双联万向联轴器输入轴与输出轴之间的转角差和角速度差发生改变，从而造成联轴器产生不稳定的扭转振动。

为了更清楚地观察三叉式-球笼式双联万向联轴器输入轴与输出轴之间的转角差随时间的变化情况，给出0.2 s内转角差的变化情况，如图7所示。

由图5 至图7 可以看出，随着外激励的不断增大，三叉式-球笼式双联万向联轴器输入轴与输出轴之间的转角差的变化趋势几乎不变，但其幅值的整体波动程度越来越大。在单个变化周期内，输入轴与输出轴之间的转角差的波动程度几乎不变；正向转角差的最大值由6.0×10-4rad增大到1.75×10-3rad，反向转角差的最大值由-7.5×10-4rad减小到-1.9×10-3rad。

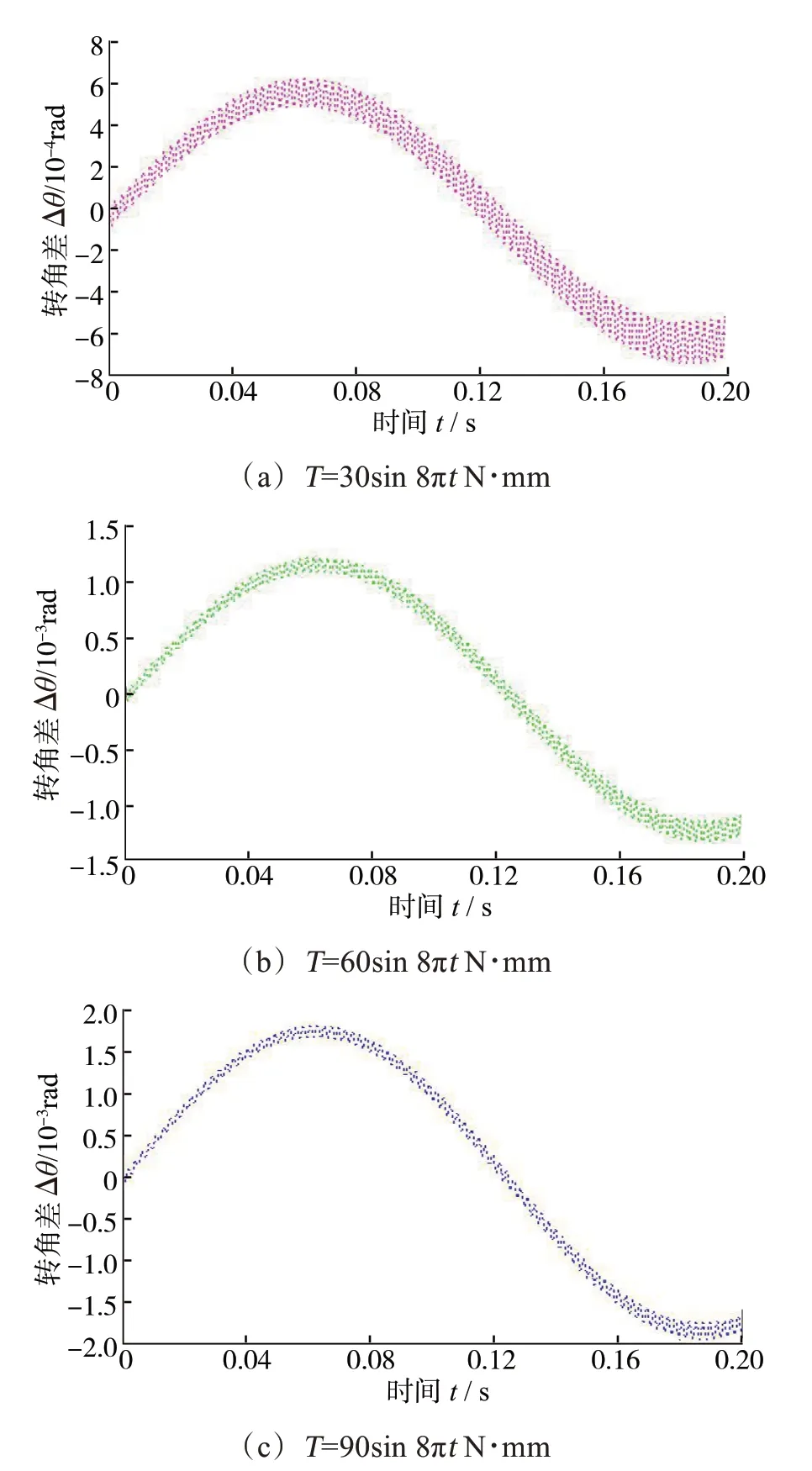
图7 0.2 s 内不同外激励下三叉式-球笼式双联万向联轴器输入轴与输出轴之间的转角差Fig.7 Rotation angle difference between input shaft and out‐put shaft of tripod-ball cage double universal coupling under different external incentives within 0.2 s

4 结论

1）利用Runge-Kutta 算法对三叉式-球笼式双联万向联轴器的振动方程进行了求解，并通过MATLAB软件进行了数值仿真分析，得到该双联万向联轴器的固有频率均为440.99 Hz，即理论计算结果与数值仿真分析结果一致，验证了仿真分析的正确性。

2）在整个三叉式-球笼式双联万向联轴器中，其输入轴与中间轴的夹角的改变会影响其输入轴与输出轴之间的转速差和角速度差，进而导致联轴器产生扭转振动，夹角越大，联轴器产生的扭转振动越剧烈。外激励的存在和改变也会使联轴器输入轴与输出轴之间的转角差和角速度差产生不稳定的变化，随着外激励的增大，联轴器的扭转振动愈加剧烈。研究结果为三叉式-球笼式双联万向联轴器的设计、制造和应用提供了理论依据和技术支持。