电液比拟的液压油缸管路系统动态特性分析

秦 磊，吴仁智

(同济大学 机械与能源工程学院， 上海 201804)

液压油缸是液压传动中比较常见的负载驱动元件，其管路系统由油缸本身和构成回路的管路组成。外部负载决定了油缸管路系统的压力大小，在动态过程中，负载冲击对油缸管路系统压力造成不同形式的振荡脉动，振荡脉动的压力又使负载具有不同的运动动态响应[1-2]，影响液压系统的控制性能，降低其响应速度、干扰其控制信号[3-5]。高频振荡脉动的压力还会造成管路或元器件的振动[6-9]，为降低泄露，管路系统密封性能要求就会更高[10-11]。从流固耦合作用考虑，降低压力振荡脉动的频率可以提高管路系统疲劳寿命[12-13]，为抑制共振，还须进行管路系统的模态分析，并避开固有频率，甚至须避开多个模态振型固有频率[14-17]。液压油缸管路系统的动态特性与整个液压系统的性能息息相关，影响因素众多。油液的可压缩性在动态过程中不可忽略，再结合管路容腔和油缸容腔的作用，压力会因其呈现出不同形式的动态特性[18-21]；油液黏性作用消耗了能量，动态过程中其对振荡脉动压力起到阻尼的作用；外负载具有惯性、弹性等机械特性，与液压油缸管路系统中的压力振荡脉动存在耦合作用[22]。在此多重因素的影响下，液压油缸管路系统的动态性能呈现出复杂的、难以预判的情形，需进行深入的机理研究。

电、液均遵循能量守恒定律，都具有闭合回路的通性，本文尝试将电路、液压回路建立关联用以研究液压油缸管路系统的动态特性，通过电、液比拟，将液压油缸管路系统的各相关参数与电路模型建立对应关系，再运用“基尔霍夫电压/电流定律”类比研究液压压力、流量等参数的动态特性，为液压油缸管路系统中压力振荡脉动的研究提供一种新的方法，此外，在液压系统的控制性能上，从液压管路层面提供更优的方法。

1 电路与液压管路的参数对应关系

电容、电阻和电感等元件是电路中的基本元器件，衡量动态特性的变化量为电压、电流。液压油缸管路系统的动态特性影响因素可分为3类：液容、液阻和液感，衡量动态特性的变化量为压力、流量。液容与液压油的体积模量、管道的弹性模量相关；液阻与液压油的黏性相关，会造成压力损失；液感与液压油的密度相关，会使一定质量的油液具备维持原有运动状态的能力。液容和液感、电容和电感仅发生能量的转换、没有损耗，能量转换是可逆的；液阻、电阻作用发生了能量损耗，这是不可逆的。电路与液压管路之间的参数对应关系如表1所示。

表1 电路、液压管路参数对应关系

电容、液容在动态过程中是电压、压差的微分函数，电感和液感在动态过程中分别是电流和流量的微分函数，参数间再进行转换又需进行积分，积分结果与参数的初始值有关，微分或积分函数的存在使得电路或管路具备一定的动态响应过程。

2 液压油缸管路系统的电路化模拟

2.1 液压油缸管路系统电路化建模

将液压油缸元件及其驱动的负载作为液压管路系统的一部分，建立图1所示的液压油缸管路系统，油缸杆及负载的总质量为m，负载弹性系数为k，负载阻尼系数为c，油缸大腔压力为p(t)，油缸大腔活塞有效截面积为A，油缸大腔进油体积流量为Q(t)，不计重力影响。

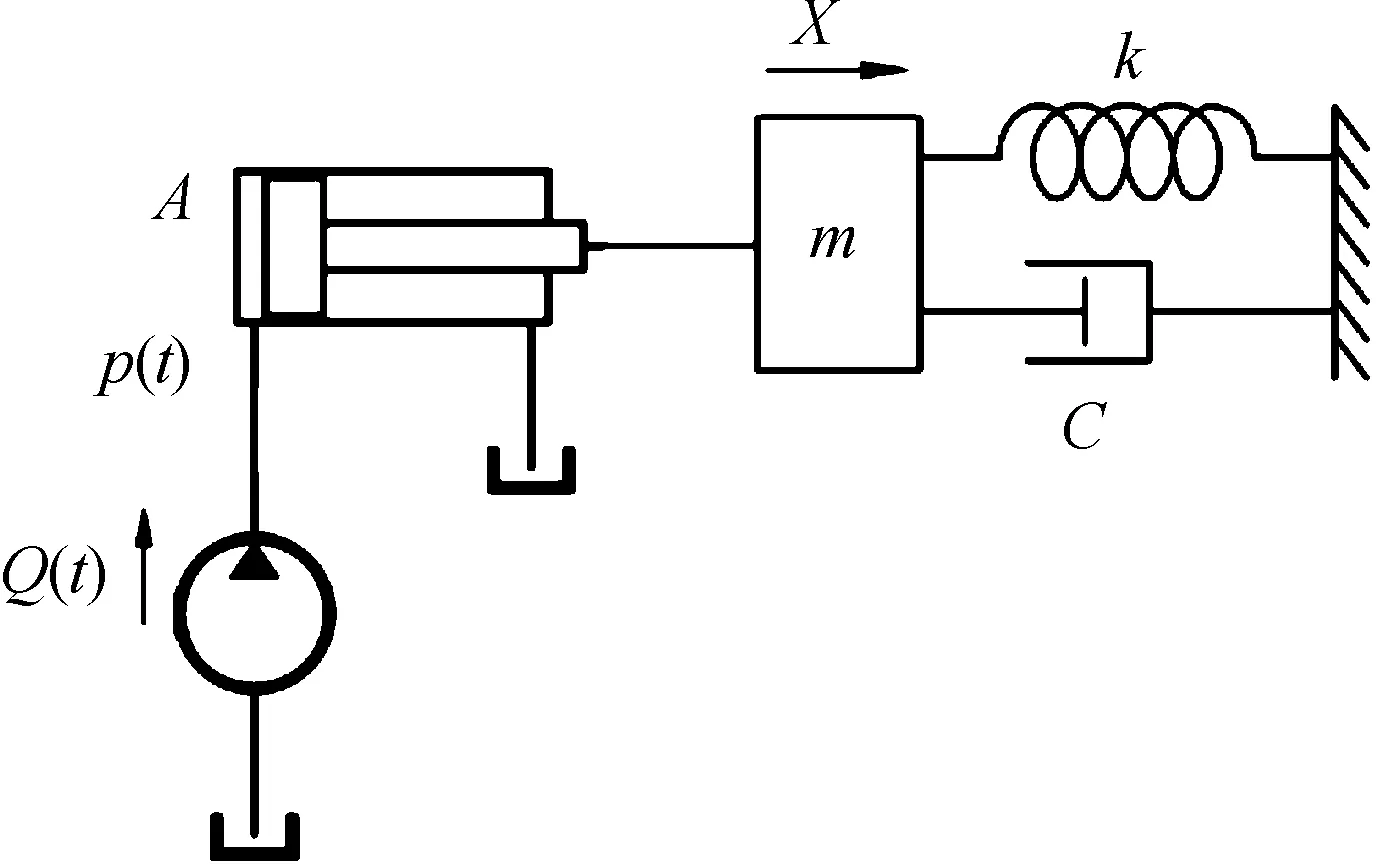
图1 液压油缸管路系统示意图

建立液压油缸的动力学方程为

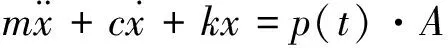
(1)

式中：x为油缸杆或负载的运动位移，正方向如图箭头所示。

(2)

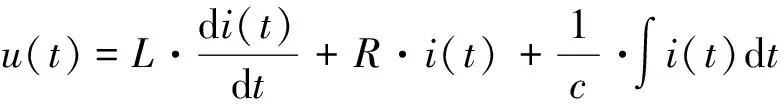
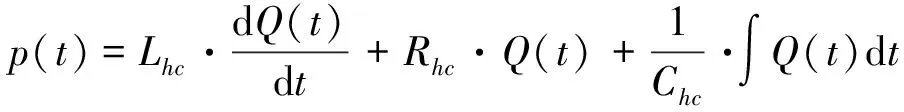
(3)

建立电路与式(3)的等效回路，得到图2。

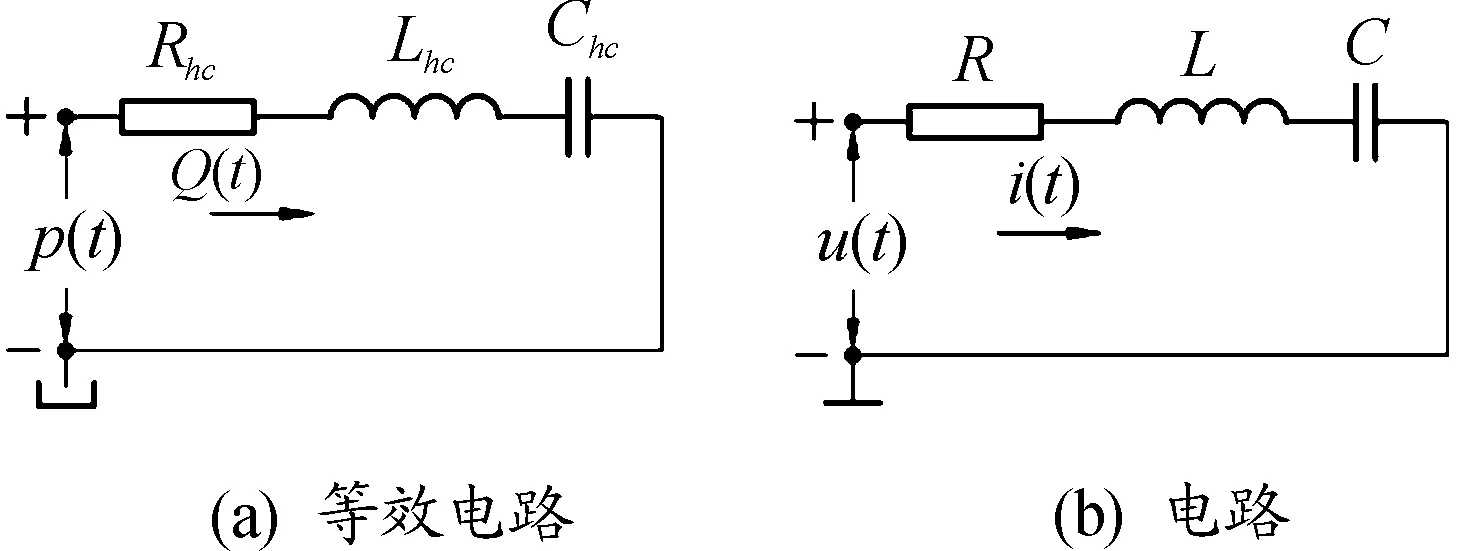
图2 液压油缸管路系统的等效回路与电路对应关系示意图

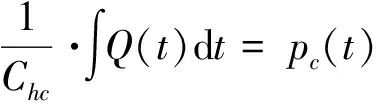
(4)

对式(4)进行拉普拉斯变换，得

RhcChc[s·Pc(s)-pc(0)]+Pc(s)

(5)

转换后，可得

(6)

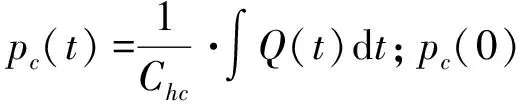
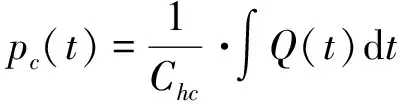
2.2 液压油缸管路系统的动态特性

为更直观表现液压油缸管路系统的动态性能，采用数值仿真的方法进行研究，设定的初始参数值如表2所示。

表2 液压油缸管路系统仿真初始参数

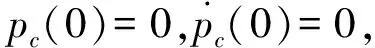
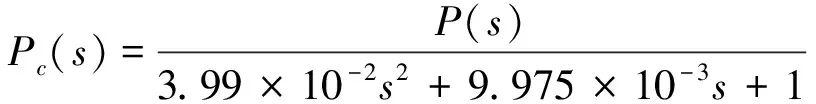
(7)

式中：各参数含义同式(6)，其他相关元件参数的动态响应方程为：

液感端压力响应

(8)

液阻端压力响应

(9)

流量响应

(10)

对应式(7)～(10)的数值仿真结果如图3所示。

从图3可看出：液压油缸管路系统中液容压力pc(t)、液感压力pL(t)、液阻压力pR(t)、流量Q(t)均呈周期衰减振荡，t→∞时稳态值均收敛，pc(t)|t→∞=13.5 MPa，pL(t)|t→∞=0 MPa，pR(t)|t→∞=0 MPa，Q(t)|t→∞=0 m3/s，[pc(t)+pL(t)]|t→∞=13.5 MPa。结合图3(e)，动态过程中，液容和液感单独作用时振荡幅值较大，压力振荡脉动中起主要作用，而pc(t)+pL(t)综合作用的振荡幅值却较小。因此，液压油缸管路系统中的压力振荡使得液感与液容之间发生较大的能量互换，剩余未参与互换的较少能量在液阻中被损耗掉。由式(2)或(3)、式(10)可知，由于函数间的耦合作用，流量也存在振荡。

图3 液压油缸管路系统各参数动态响应数值仿真曲线

2.3 压力振荡脉动的控制方法

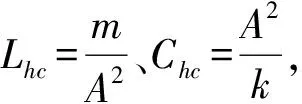
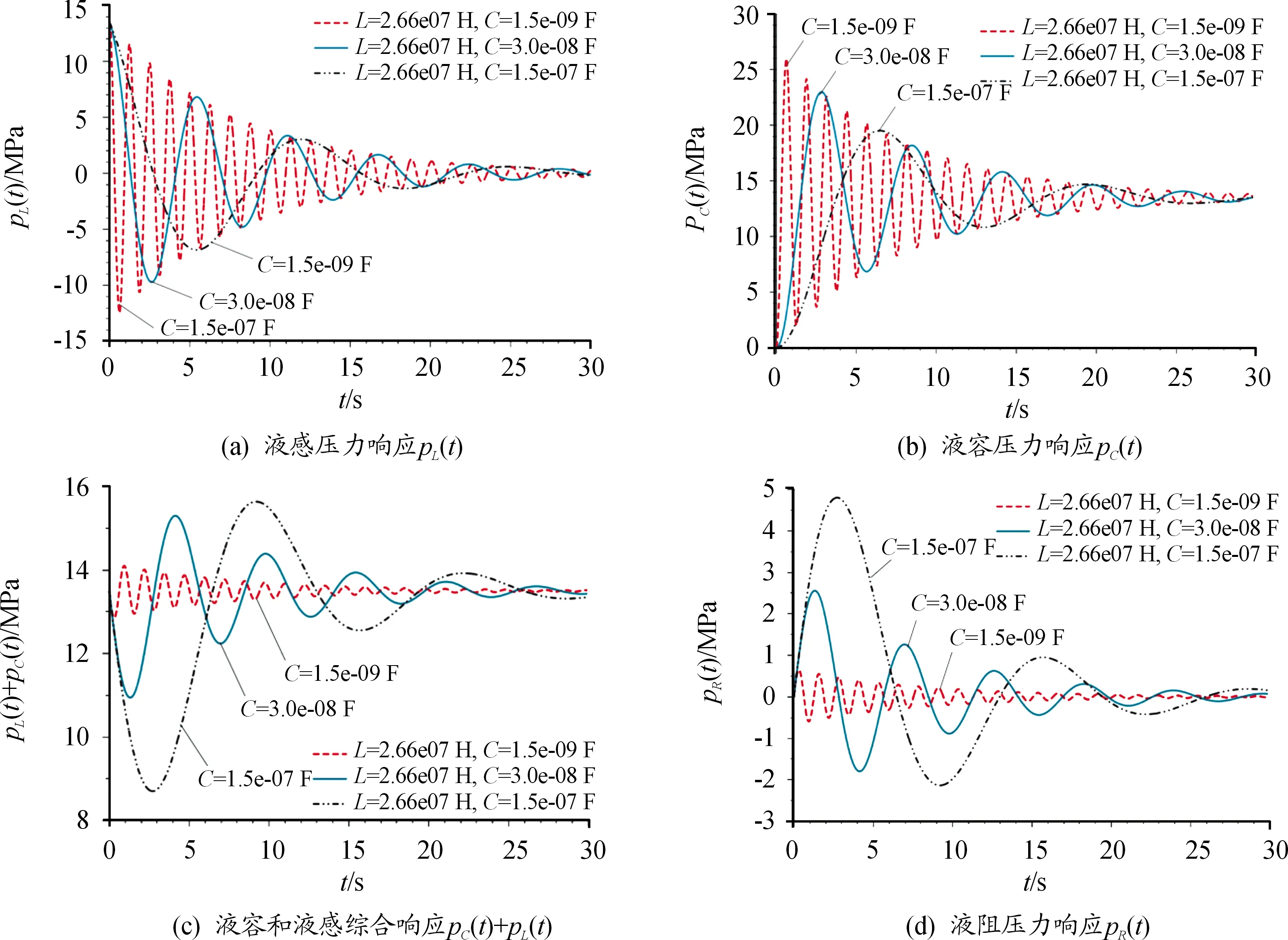
图4 油缸管路动态响应曲线：液感为定值、液容为变量

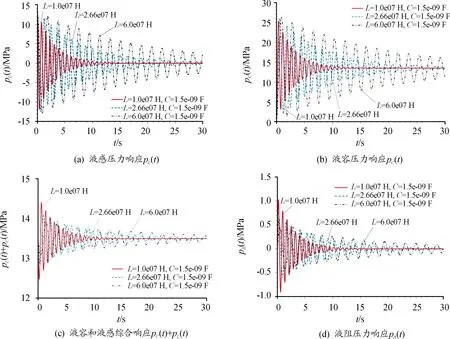
图5 油缸管路动态响应曲线：液容为定值、液感为变量

从图4可以看出：液感为定值，随着液容的增加，各参数的振荡脉动频率都减小，但幅值有差别，图4(a)、(b)液容和液感独立作用的幅值外包络线恒定，最大幅值不变，各参数下的超调量相近，而且，液容和液感的响应始终保持相位相差180°。图4(c)液容和液感综合作用的幅值有较大变化，液容越大、综合作用的最大幅值越大，图4(d)液阻响应与图4(c)综合响应基于稳态值为平衡中心时等值反相(相位差180°，基于稳态值为零点时最大幅值相同)。因此，液压油缸管路系统中，液容和液感的存在使得油液中的压力存在振荡脉动，其幅值受液容和液感的综合影响，综合影响的压力值等值反相作用于液阻上。

从图5可以看出：液容为定值，随着液感的增加，各参数的振荡脉动频率均减小，图5(a)、(b)幅值的外包络线均向外扩大，即最大幅值随液感增加而增加，而且，液容和液感的响应同样是始终保持相位相差180°。图5(c)中，在初始时刻，较大的液感可以降低超调量，但振荡的衰减却随液感的增加而越缓慢(调节时间变长)。图5(d)液阻响应与图5(c)综合响应基于稳态值为平衡中心时也具有等值反相的规律(相位差180°)。

再结合对比图4(c)和图5(c)，图4(c)中随着液容的减小、综合响应的振荡脉动幅值减小，图5(c)中随着液感的增加、综合响应的振荡脉动幅值却增大，据此，可推定，可能存在相匹配的液容和液感组合，使得综合响应的振荡幅值为零、压力的振荡脉动完全被抑制，此时，需要液感响应和液容响应具有相同的频率、相同的幅值、相差180°的相位角，为验证这一推定结论并对其求解，从方程的理论推导进行分析。

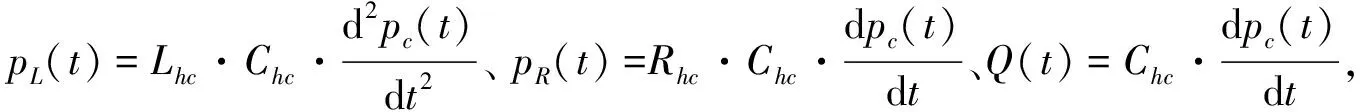
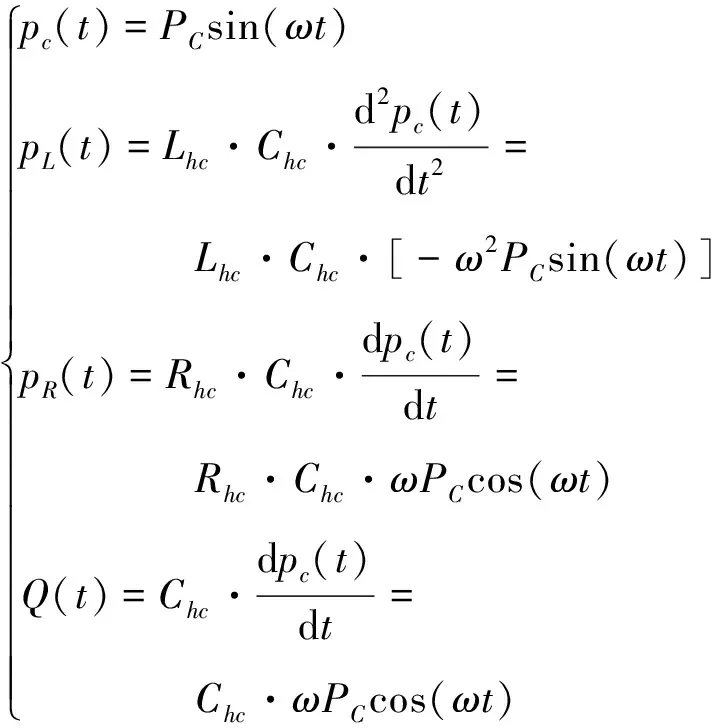
(11)

将式(11)统一成正弦项的函数，得到

(12)

由式(11)和(12)可见，不同方程间的变换仅存在微分、积分，且幂次数最高为1，对于正弦或余弦项，无论进行多少次的微分或积分，都不会改变圆频率ω的大小、有变化的仅为初始相位角(如式(12)中的0°、90°、180°等)，这样，在公式推理中就可不需考虑正弦/余弦量中的圆频率角度ωt而仅考虑初相位角度，在同一激励下，液容、液感、液阻和流量等参数的动态响应具有与激励相同的圆频率ω，存在区别的是幅值和相位，故在各参数的频率保持相等的情况下，公式理论推理过程中可先不考虑ω参数项，在最终的计算结果中再直接代入含ω的不变项即可。本文统一采用正弦量进行计算(同式(11)转换为式(12)，余弦量可变换为正弦量)，这种处理正弦量的方法，便可采用相量用以表达正弦量，采用相量的方式对式(12)中的各个正弦量进行表达，得到

(13)

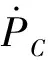
式(13)对应的相量图如图6所示，其中逆时针旋转方向的角度为正。

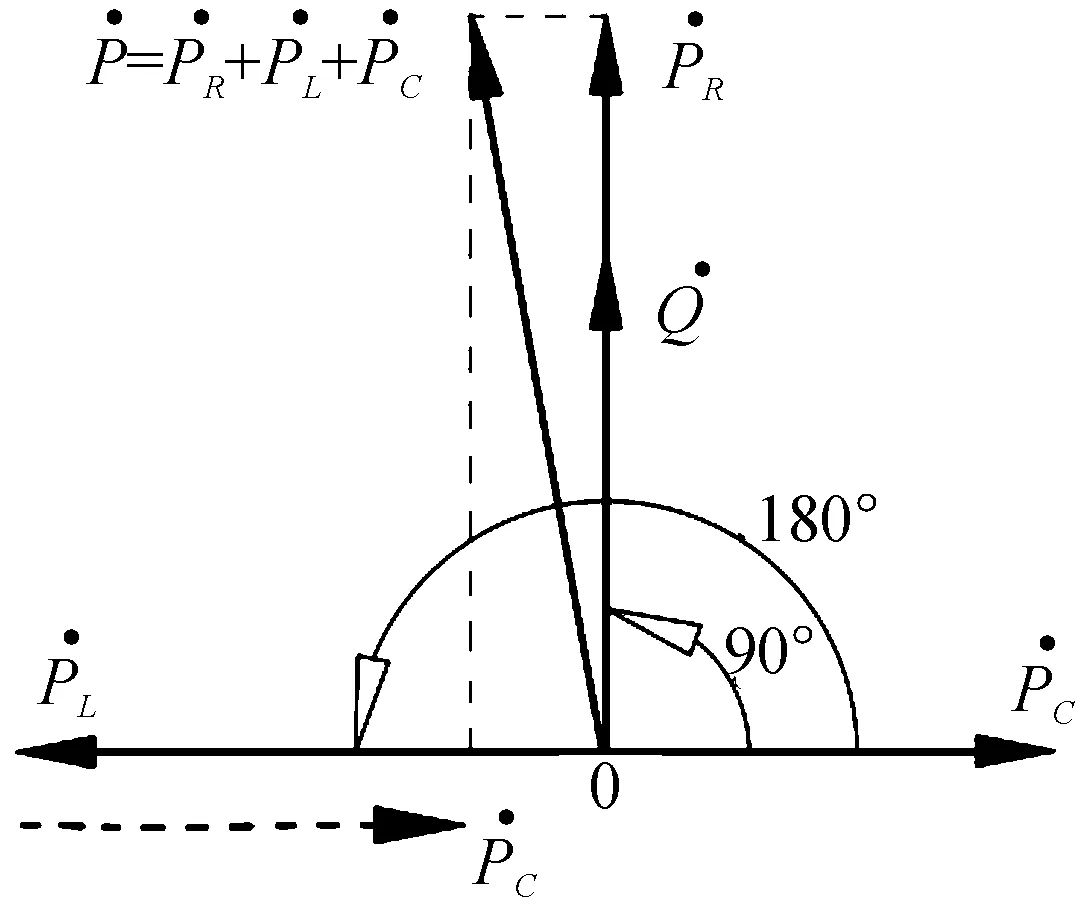
图6 液容、液感、液阻和流量的相量图

(14)

PC=LhcChcω2PC

(15)

PC明显非零，进一步变换，得到

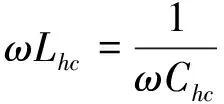
(16)

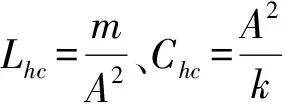
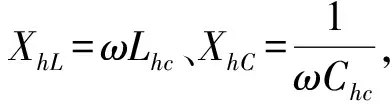
XhL=XhC

(17)

因此，要消除液感和液容的综合影响，所需的必要条件为满足方程(17)即可。

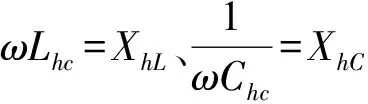
(18)

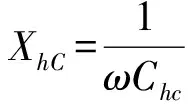
返回到式(17)可知，要使得液容和液感的综合影响得以相互抵消消除，需要满足液感抗XhL与液容抗XhC相等的条件。现在来推导使XhL=XhC实现的方法及具备的条件。

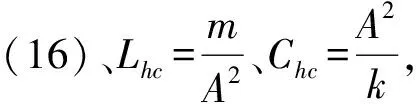
(19)

基于表3的数据，可得液感Lhc=2.66×107H；液容Chc=1.50×10-9F；液阻Rhc={2.66×107，1.33×108，2.66×108，5.32×108}；油缸大腔压力p(t)=13.5 MPa以阶跃形式加载；系统具有零初始条件，基于式(6)～(10)得到液压油缸管路系统的动态响应如图7所示。

表3 液压油缸管路系统仿真初始参数

图7 不同阻尼比液压油缸管路系统动态响应曲线

由图7(a)～(d)可知，负载阻尼比的变化改变了外负载共振固有频率的同时，也改变了油缸管路系统中液容、液感、流量、液阻等参数动态响应的频率，前述推论得到证实。在阻尼比0<ζ<1的欠阻尼情形中，油缸管路系统各参数具有衰减振荡的特性；ζ≥1为临界阻尼(ζ=1)和过阻尼(ζ>1)情形，液容的压力响应无振荡性、超调量为零，液感、液阻和流量等参数的动态响应仍呈现振荡性、且超调量与ζ近似反比。在整个动态过程中，负载作用产生的阶跃压力使管路系统流量初始时负向流动，液容从负向流量中吸收并储存压力能量，液感使管路中压力出现脉动振荡、并与液容能量互换。

结合图7(e)，液容和液感综合作用的动态响应中，初始时压力从平衡点(13.5 MPa)瞬时骤降、随后在波谷瞬时上升，最终稳定于平衡点(13.5 MPa)，阻尼比越大、波谷的位置越低，波谷并未越过零值，因此波谷降低了管路中的压力。在ζ≥1时，液容和液感的综合响应不再有周期振荡特性，最大压力值不超过平衡点压力(13.5 MPa)，这种情形即存在液容和液感相互抵消消除的综合作用，压力振荡脉动得到抑制。从控制性能上考虑，为消除压力振荡脉动，需使ζ≥1、超调量始终保持为零，但ζ越大，调节时间、上升时间就会增大，不利于控制的快速性、精确性，因此ζ≈1即可满足综合要求，这时外负载系统处于临界阻尼状态、没有周期振荡，也使液压油缸管路系统的动态响应没有振荡脉动，同时又使整个液压油缸系统具备调节时间和上升时间较适宜的控制性能。

需要说明的是，流量的流动是有方向的，液感产生的压力响应可为正、可为负，对应于油液压力能和动能的转换关系，在图7(a)中出现的较大的负压反映的是液感的压力回收，将动能转换为压力能，而正压表示压力能转换为油液动能，液感的正、负压不是实际管路中的压力测量值；考虑流量方向后，液阻的压力响应也可为正、可为负，如图7(d)所示，为正时说明流量与原参考设定的方向一致、为负时说明流量与原参考设定的方向相反，类似于电路中的参考电压、参考电流方向的设定。

3 结论

1) 液压油缸管路系统中的压力振荡脉动由液容、液感引起，液容和液感之间发生液压能量的相互转换，两者间的能量转换是可逆的。

2) 液容抗XhC=液感抗XhL时，液容和液感之间产生的压力振荡脉动可以相互抵消，此时液容和液感综合作用的压力脉动幅值最小。压力振荡脉动的频率与油缸驱动的外负载无阻尼固有频率相等，即发生共振时，可以获得XhC=XhL。

3) 为得到最优控制性能，使外负载阻尼比ζ≈1处于临界阻尼状态时，与之相匹配的液压油缸管路系统的压力动态响应频率接近零、不具有振荡脉动特性、油缸管路系统与外负载的共振被抑制，控制性能上的调节时间和上升时间综合性能较优、超调量接近零。