基于柔度曲率差变化率的悬索桥损伤识别分析
王雪忠,赵 青
(安徽建筑大学 土木工程学院,安徽 合肥 230601)
0 引言
一种良好的损伤识别指标应能精准判断结构是否发生损伤,以及损伤位置、损伤程度.早期Pandey等[1]提出基于柔度矩阵来识别结构是否发生损伤以及损伤位置,实验结果表明,只需前几阶模态参数就可以检测出结构的损伤位置.紧接着Pandey等[2]提出基于模态柔度矩阵差的损伤研究,随后大量的研究人员把该方法很好地运用在简支梁结构和板形结构的损伤识别中[3-4],都取得了很好的效果.在此研究的基础上不少研究人员提出了曲率模态差、模态柔度差、模态曲率改变率、柔度曲率差变化率等指标[5-11],上述损伤识别指标基本都可以精准识别出结构损伤以及损伤位置.但柔度曲率差变化率的损伤识别方法对悬索桥的研究鲜少报道.
本文采用一种基于柔度曲率差变化率的损伤指标方法[12],对悬索桥(吊杆和加劲梁)进行多种损伤工况情况下的数值模拟和损伤识别分析,验证这种损伤指标的可行性和有效性.
1 损伤识别指标理论分析
由Pandey等[1]提出的模态柔度矩阵表达式为
(1)
式中:n为模态阶数;φi、ωi分别是结构的第i阶模态振型向量(最大位移正则化[13])和相对应阶的固有频率.
悬索桥是低刚度和低阻尼的柔性结构,对振动非常敏感,表现出复杂的振动特性[14].一旦结构发生损伤,其振型和频率必然发生改变[15].
将式(1)中所得到的A进行一次行差分得到柔度矩阵
(2)
式中:Aj为柔度矩阵第j列元素;l(i-1)i、li(i+1)、l(i-1)(i+1)为下标2单元之间的距离.
经一次差分计算后,柔度矩阵将从n×n的方阵变为(n-1)×n的柔度矩阵.对柔度矩阵B再进行一次列差分得到曲率矩阵
(3)
式中:Bj为矩阵第j行元素.
经过二次差分计算,C为(n-1)×(n-1)柔度矩阵的曲率方阵.
将结构损伤前后的柔度曲率矩阵做差得到差矩阵
D=Cu-Cd,
(4)
式中:Cu表示无损柔度曲率;Cd为损伤柔度曲率.
王立宪等[16]提出基于柔度矩阵主对角斜率的结构损伤识别方法,为了提高损伤指标的敏感性,进一步放大无损伤与损伤之间的差异,在此基础上,对差矩阵D取对角线主元素用E表示,并再对E做一次差分即得到柔度曲率差变化率指标:
E=diag(D)=[d11…dii…d(n-1)×(n-1)],
(5)
FCDR=diff(E)=[ε1,…,εi,…,ε(n-2)].
(6)
通过Matlab绘制损伤指标FCDR于识别曲线图上,图中横坐标为结构节点号所对应位置,纵坐标为损伤诊断指标幅值,幅值出现的位置表示损伤发生位置,幅值绝对值的大小表示损伤严重程度.
2 悬索桥模型及有效性验证
2.1 建立模型
本文研究对象是某悬索桥,全桥长650 m,两边边跨为125 m,主跨为400 m.用有限元软件Midas Civil对其悬索桥进行空间建模分析,模型共有269个节点,270个单元.其中加劲梁单元有52个,吊杆单元有98个.如图1所示.

图1 悬索桥有限元模型
本文旨在验证指标损伤识别的可行性和有效性,对结构损伤模拟通过在有限元Midas Civil中降低材料的弹性模量来实现,在模拟损伤过程中出现的非线性状态特征和损伤程度的精确模拟不做深入探讨,损伤模拟中损伤单元质量和截面尺寸不变.加劲梁和吊杆编号如图2~3所示.各模拟工况如表1所示.

图2 加劲梁编号

图3 吊杆编号

表1 各个损伤工况
2.2 损伤识别指标分析与验证
使用有限元Midas Civil分别提取加劲梁和吊杆损伤前后的前5阶模态参数并做最大位移正则化[13]处理,将所提取的数据导入Matlab软件中,并编写程序进行计算与处理.最后绘制损伤指标FCDR曲线图分析,图中横坐标为结构节点号所对应位置,纵坐标为损伤诊断指标FCDR的幅值.(在此特意说明:由于是用节点号来进行数据处理,多点损伤是从54号至250号,所以吊杆63、91、112、140号单元所对应的节点号分别是(74,75)、(130,131)、(172,173)、(228,229),在此基础上减去54所得的结果才是对应单元的节点号).单点损伤和多点损伤分别如图4~5所示.
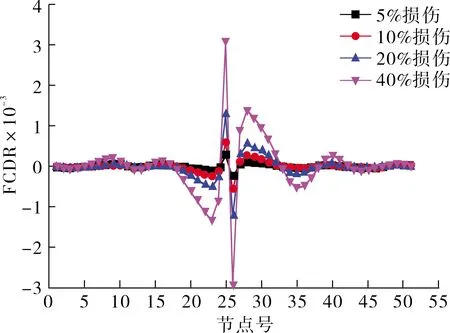
图4 梁26号单元不同程度损伤
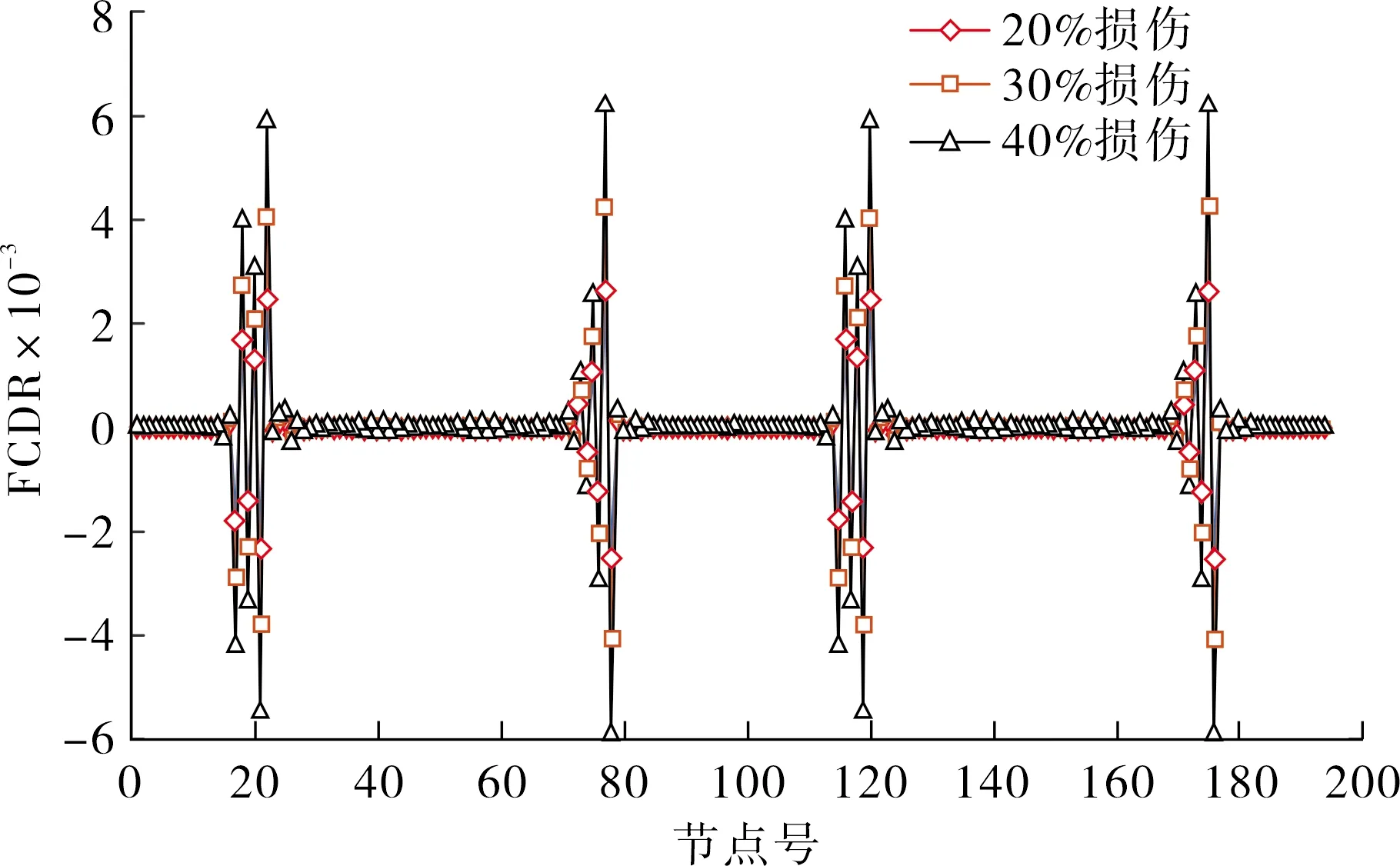
图5 吊杆63、91、112、140号单元不同程度损伤
图4~5中损伤指标FCDR最大值如表2~3所示.

表2 梁26号单元损伤指标FCDR最大值
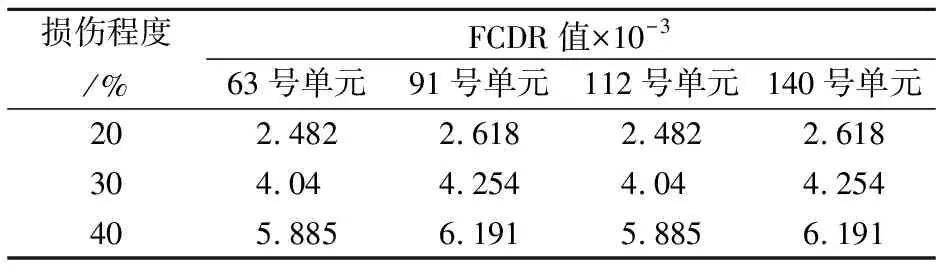
表3 吊杆单元损伤指标FCDR最大值
结合图4和表2中的FCDR曲线和最大值不难得出,5%、10%、20%、40%损伤曲线都在26号单元处出现了幅值和突变,且随着损伤程度的递增其幅值也在变大,突变更加明显.在5%的损伤程度情况下,损伤指标FCDR能够很好的识别出来,体现出这种损伤识别方法对损伤的敏感度很高.损伤程度与损伤指标FCDR最大值成正比.突变和幅值出现的位置和程度能够精确的反应出损伤发生位置和损伤程度,同时26号单元临近的单元也出现了小波动的幅值和小幅度的突变,说明某处单元的损伤对临近单元有所影响.
通过图5和表3中的FCDR曲线和最大值可以明显看出,20%、30%、40%损伤曲线分别在63、91、112、140号单元处出发生了突变,其幅值也出现在这4个单元处.随着损伤程度的增大其幅值也在变大,突变更加显著,损伤程度与损伤指标FCDR最大值成正比列.在表3中可以发现63号单元和112号单元、91号单元和140号单元在各个损伤程度下,其损伤指标FCDR最大值都是一样的,这是因为63号单元和112号单元、91号单元和140号单元分别连接着同一单元的加劲梁.突变和幅值出现的位置和程度能够精确的识别出损伤发生位置和损伤程度.换句话说,当FCDR曲线中某单元2节点号出现绝对值最大的幅值,说明此单元有损伤.同时这4个单元临近的单元也出现了小波动的幅值和小幅度的突变,说明某处单元的损伤对临近单元有所影响.
上述分析的是单一构件的各个损伤工况情况,为了进一步研究损伤指标FCDR对哪种构件的损伤更为敏感,现使用有限元Midas Civil模拟加劲梁和吊杆同时损伤.损伤工况如表4所示.

表4 加劲梁和吊杆同时损伤工况
通过Matlab编程计算与数据处理得到损伤指标FCDR曲线如图6所示.
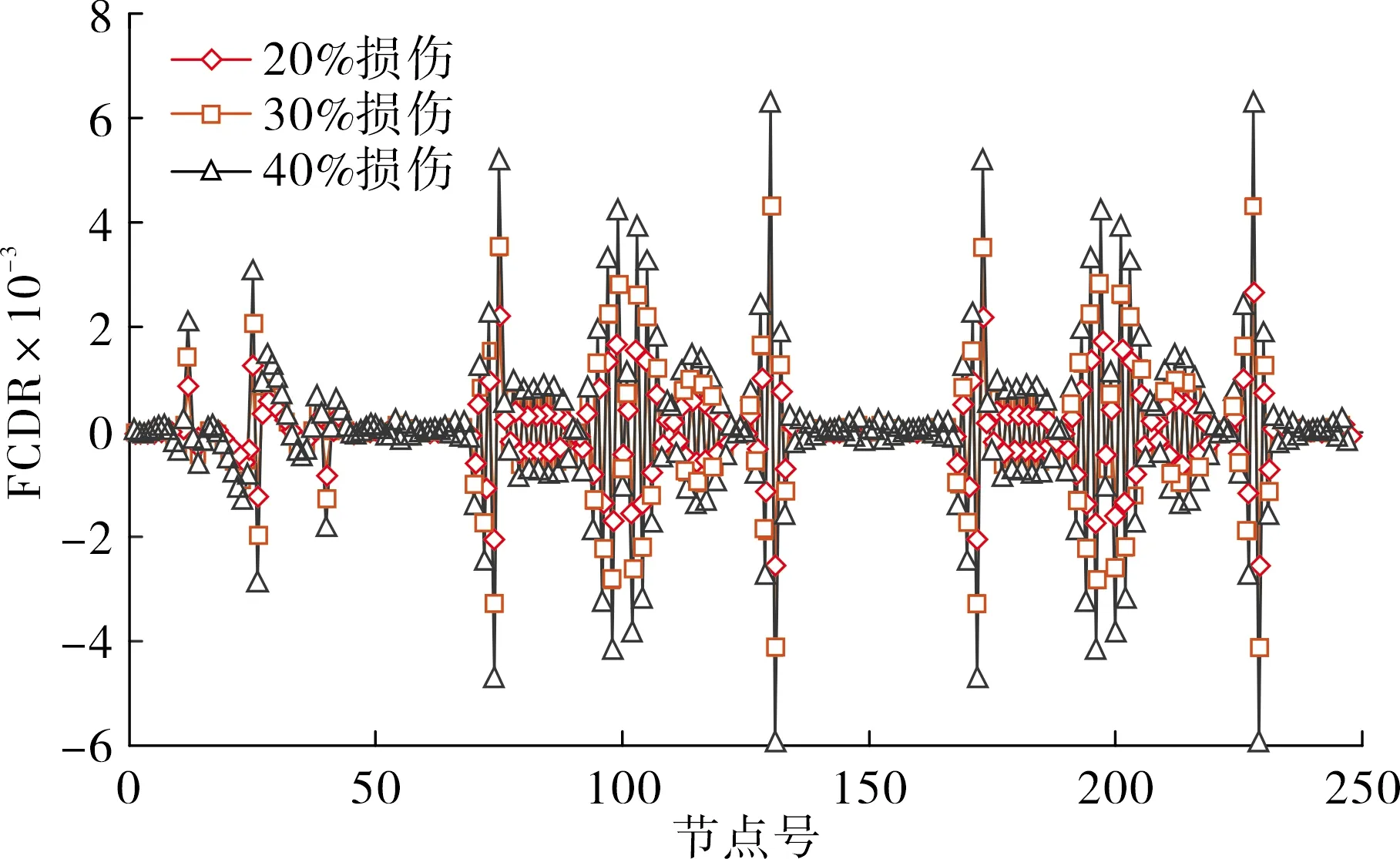
图6 26、63、91、112、140号单元不同程度损伤
通过图6可以看出:尽管是加劲梁和吊杆同时损伤,损伤指标FCDR也能够精准的全部识别出损伤位置和损伤程度,且随着损伤程度的增加,损伤识别效果更明显.在同一损伤程度下,吊杆的幅值大于加劲梁的幅值,说明损伤指标FCDR对吊杆构件的损伤更为敏感.结合图4~5可以看出:加劲梁和吊杆单一构件的损伤对临近单元的影响范围小于2构件同时损伤对临近单元的影响范围.损伤的吊杆对其所连接的加劲梁会产生一定的影响,同时损伤的加劲梁对其所连接的吊杆也会产生一定的影响,且损伤的加劲梁对其所连接的吊杆影响大于损伤的吊杆对其所连接的加劲梁影响.说明构件的损伤对其所连接的构件也会产生影响,在此又体现出损伤指标FCDR对吊杆构件的损伤更为敏感.
3 结论
1) 在损伤程度不同、损伤工况不同、单点损伤或多点损伤时,损伤指标FCDR都能精确的判断出损伤位置和损伤程度.说明此方法在损伤识别中效果很好,可结合实际工程应用.
2) 5%的损伤也能精确识别出来,说明损伤指标FCDR对损伤很敏感.随着损伤程度的增大其幅值也在变大,突变越明显,且损伤指标FCDR最大值与损伤程度成正比.
3) 损伤指标FCDR对吊杆的损伤比加劲梁的损伤更敏感.构件与构件之间的损伤是相互影响的,且多种构件同时损伤时FCDR曲线图中的幅值比单一构件损伤时FCDR曲线图中的幅值更明显.

