果园运输车减振降损性能

戚得众，郭 林，阮晓松，闫行行

(1.湖北工业大学机械工程学院，武汉 430068；2.湖北省农业机械工程研究设计院，武汉 430068)

截至2019年12月31日，全中国水果产业市场规模高达25 039.4亿元，占国民生产总值的2.54%。机械损伤是水果品质下降造成经济损失的主要原因，在果园运输到物流起点的过程中，果实几乎是没有任何保护措施的，所以果实的机械损伤大多发生在这一阶段。中国是世界上最大的苹果生产国，种植面积和产量均占世界50%以上，而苹果从果园到餐桌的损耗为25%～30%。故以苹果为例，设计一种具有良好减振性能的水果运输小车，从而对减少水果损伤，提高水果经济价值具有重要意义。

李光等[1]提出了一种苹果运输包装振动损伤的预测方法。李艳聪等[2]对苹果的损伤力学特性进行了研究。冯哲等[3]对苹果静压接触应力进行了研究，通过引入修正值显著提升了苹果静压接触应力的计算精度。颜建伟等[4]对单自由度模型苹果脆值进行了研究，测得临界脆值约为96.28。尚静等[5]提出一种紫外/可见光谱技术与模式识别算法相结合测量苹果损伤的测量方法。沈宇等[6]针对苹果损伤识别的有效波段进行研究，发现811 nm为最优波段，识别率高达90.63%。张茜等[7]对建立了果品振动损伤模型，并提出减缓损伤的对策。Zhu等[8]也对苹果损伤的识别进行了相应的研究。Scheffler等[9]将离散元素法应用于苹果碰撞，对苹果的连续碰撞损伤进行了研究。Komarnicki等[10]对苹果的抗擦伤性能进行研究，提出一种预测自由落体冲击状态下苹果抗擦伤性和擦伤阈值的方法。Fazel等[11]提出一种基于ANFIS(adaptive neuro-fuzzy inference system)的苹果损伤预测方法。

诸多学者对苹果的损伤特性及损伤检测进行了研究，提供了宝贵的经验。但鲜有学者对果园运输工况下苹果损伤进行研究。在此基础上以苹果损伤率为评价标准，对设计的二级减振果园运输小车减振降损性能进行研究，建立ADAMS与EDEM联合仿真模型，通过仿真分析苹果损伤情况，以确定果园运输小车的减振降损性能。

1 理论分析

苹果在运输过程中的碰撞主要分为两种，一种是苹果与苹果之间的碰撞，另一种是苹果与果箱之间的碰撞。无论是哪一种碰撞形式，当苹果受力达到一定值时可定义苹果为损伤。

把苹果看作单个颗粒对其碰撞受力进行分析，当颗粒发生三维接触时，颗粒所受到的力由法向力Fnij及切向力Ftij两部分构成，Fnij是弹簧和法向阻尼器作用在颗粒i上的弹性力与阻尼力的合力，切向力Ftij是弹簧和切向阻尼器作用在颗粒i上的弹性力与阻尼力的合力，颗粒间简化力模型如图1所示。

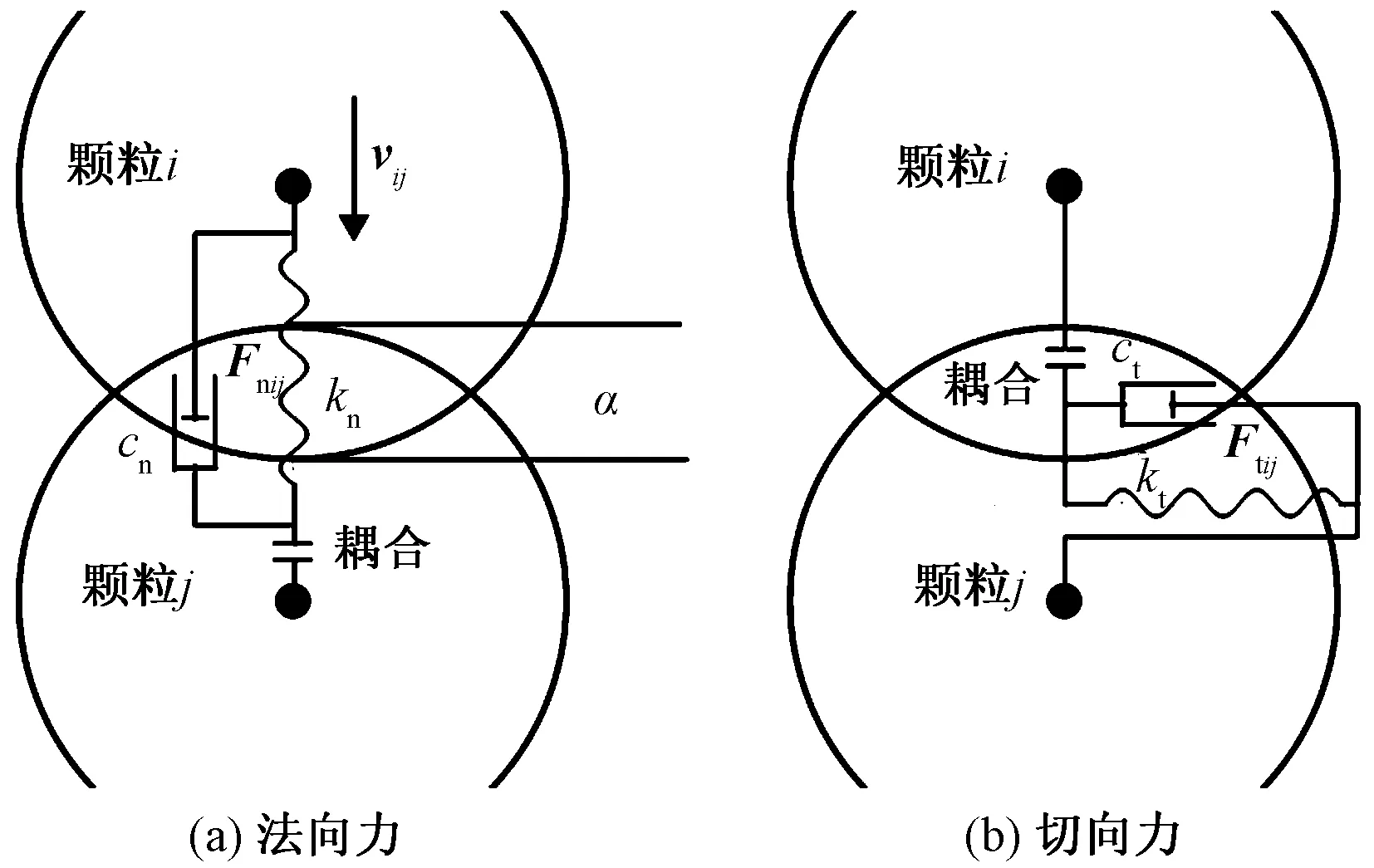
图1 颗粒间接触力简化模型

由Hertz接触理论可知

(1)

式(1)中：α是法向重叠量；vij是颗粒i相对于颗粒j的速度；n是从颗粒i球心到颗粒j球心的单位矢量法向分量；kn和cn是颗粒i的法向弹性系数和法向阻尼系数。

同理可知

Ftij=-ktδ-ctvct

(2)

式(2)中：kt和ct分别代表颗粒i切向弹性系数和切向阻尼系数；vct是接触点的滑移速度；δ是接触点的位移。

滑动速度矢量vct为

vct=vij-(vijn)n+Riωi×n+Rjωj×n

(3)

式(3)中：Ri代表颗粒i的半径；Rj代表颗粒j的半径；ωi代表颗粒i的角速度；ωj代表颗粒j的角速度，由式(2)可知vct与vij成正比。

颗粒i受到的合力为

Fij=Fnij+Ftij

(4)

当颗粒i与多个颗粒相接触碰撞时，作用在颗粒i上的总力为

(5)

法向弹性系数kn为

(6)

式(6)中:i和j分别代表发生碰撞的颗粒i和颗粒j；E代表颗粒的弹性模量；ν代表颗粒的泊松比；R代表颗粒半径。

切向弹性系数kt为

(7)

式(7)中:Gi和Gj分别代表颗粒i和颗粒j的剪切模量。

法向弹性系数kn的大小与颗粒本身的属性有关，且为一个固定值。切向弹性系数kt除了与颗粒本身的属性相关外还与法向重叠量α有关，在颗粒的接触过程中α是一个不断变化的随机变量。

颗粒在接触过程中的受力Fnij的大小与vij成正比，力Ftij的大小与vct成正比，且vct与vij成正比，所以在其他条件不变的情况下，颗粒i与多个颗粒相接触碰撞时，作用在颗粒i上的总力Fi与vij成正比，可以通过减小vij来减小Fi，以降低颗粒接触碰撞时造成的损伤。

苹果在运输过程中碰撞受力与vij成正比。果园运输车工作时在路面激励的作用下，果箱会产生振动，振动的剧烈程度决定vij的大小。须对运输车的减振结构进行优化，提高运输车的减振性能，降低运输过程中的苹果损伤率。

2 联合仿真模型建立

2.1 ADAMS模型建立

南京农业机械化研究所的徐竹凤等[12]对果园不平度进行了研究，最后通过测量得出了丘陵山地果园的路面等级在C级到D级之间。针对山地智能运输小车的使用场景，以北方的苹果园为例，选择C级路面。当小车以1 m/s的速度行驶在C级路面，MATLAB生成路面不平度如图2所示。

图2 果园路面不平度

对如图3所示三种不同悬架系统的果园运输车进行仿真分析。小车a 采用摆动平衡肘、旋转弹簧旋转阻尼单元悬架系统，小车b采用摆动平衡肘、平动弹簧平动阻尼单元悬架系统，小车a和小车b为目前应用最广的两种履带运输车，但其减振性能一般。为了提高履带运输车的减振性能，设计出小车c，小车c在小车a的基础上采用二级减振结构，果园运输车二级减振结构动力学模型如图4所示，相关参数如表1所示。

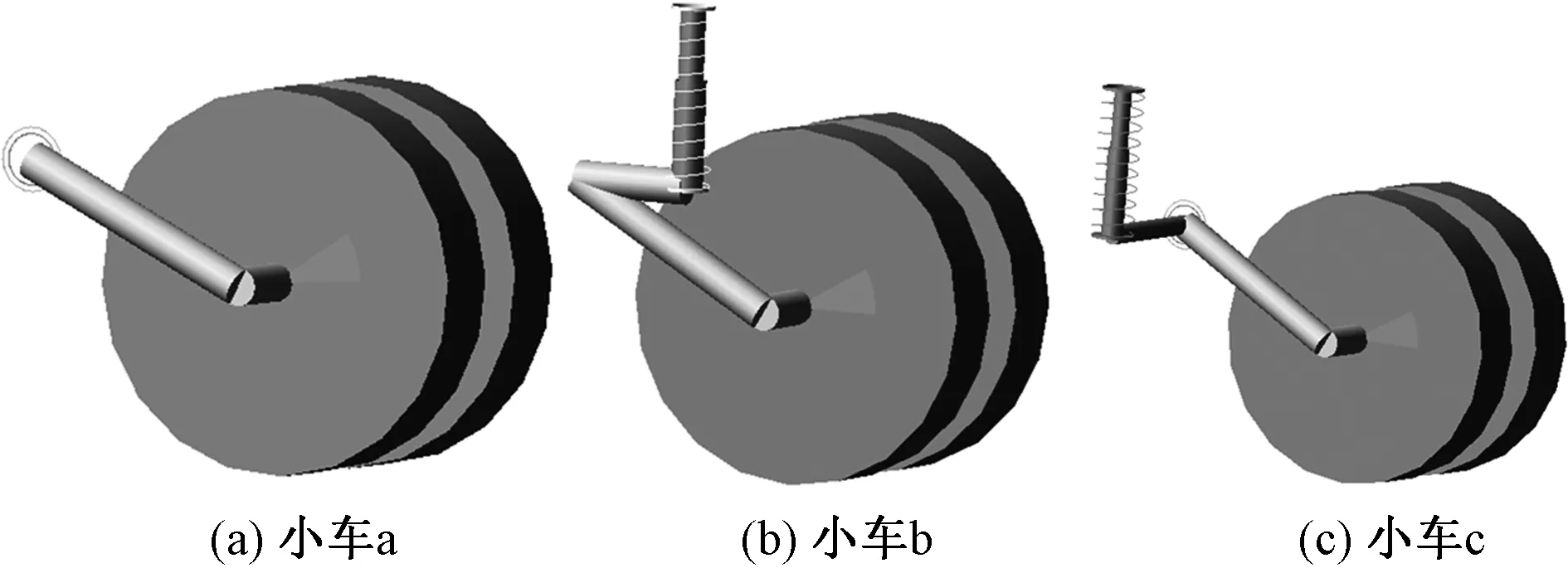
图3 果园运输车悬架系统

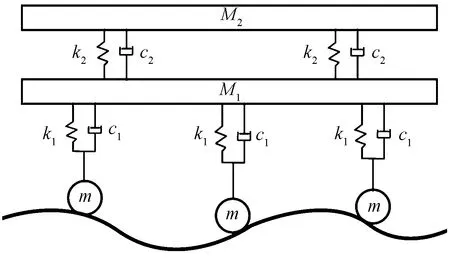
图4 果园运输车半车动力学模型

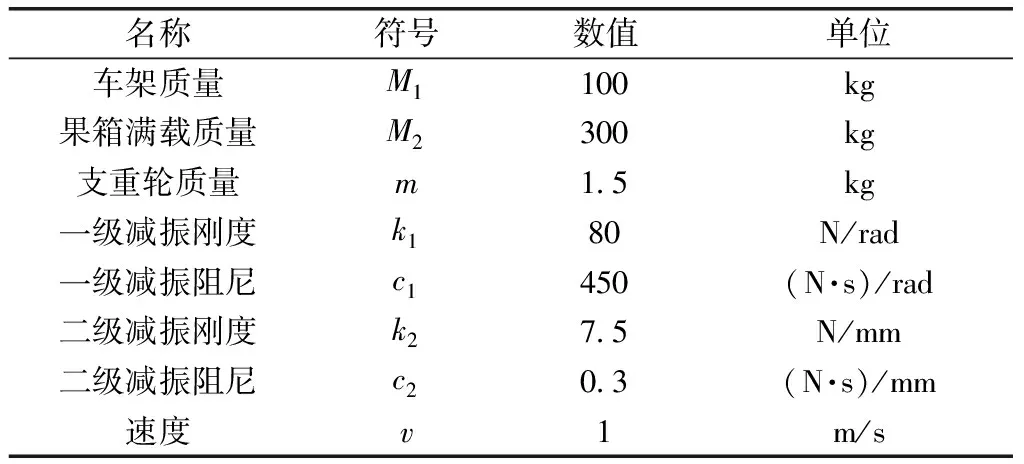
表1 果园运输车相关参数值

果园运输车采用三种减振结构，以1 m/s的速度在构建的c级路面上行驶20 s，通过ADAMS仿真得到果箱在时域上的加速度响应，将其导入EDEM作为果箱的运动特性。

2.2 EDEM模型建立

EDEM能够模拟颗粒与颗粒及颗粒与几何体碰撞的运动过程和能量传递过程，采用EDEM对果园运输车在丘陵山区果园工作时果箱内苹果受力进行分析。将苹果模型简化为颗粒模型，简化前后苹果三维模型如图5所示。果箱简化为方形几何体，其运动特性为ADAMS仿真结果，仿真时长为20 s，步长为0.1 s。

图5 苹果三维模型图

中外的诸多学者对苹果的材料属性进行了测量研究[13-17]，研究结果表明苹果的弹性模量在3～5 MPa之间，泊松比在0.35附近，苹果与苹果之间的动态摩擦系数为0.26±0.3，苹果与金属间的动态摩擦系数为0.27±0.8，颗粒仿真具体参数如表2所示。

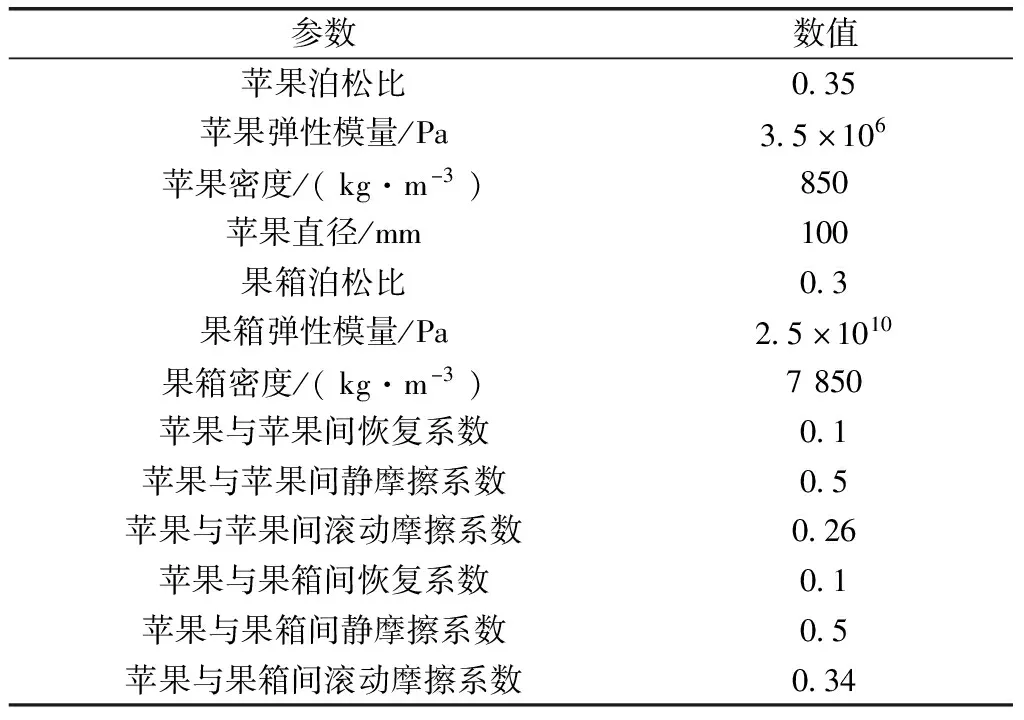
表2 仿真参数设置表

3 仿真与分析

3.1 碰撞过程分析

苹果是软质物体，具有一定的黏塑性，苹果与苹果发生碰撞时，首先发生的是弹性变形，这个阶段果肉不会有明显损伤，当压力超过生物屈服极限后，苹果的果肉组织会发生局部破坏，进入塑性变形阶段。当压力到达破坏极限时，苹果开始出现明显是宏观损伤。Fu等[18]对苹果碰撞损伤进行研究，发现当碰撞受力低于68 N时，96%的苹果可以达到售卖标准。根据GB/T 10651—2008中苹果二等果总损伤面积不得超过1 cm2(100 mm2)，单处损伤面积不得超过0.3 cm2(30 mm2)的规定，以60 N为碰撞损伤的阈值。

苹果在运输过程中的碰撞如图6所示。

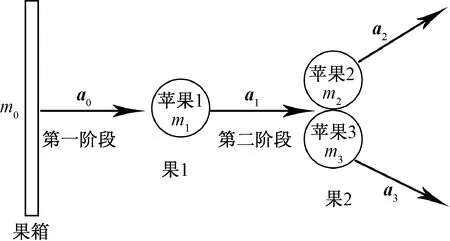
图6 苹果碰撞过程示意图

其中果1和果2分别代表直接和果箱碰撞的苹果以及间接与果箱碰撞的苹果，m0、m1、m2和m4分别是果箱、苹果1、苹果2和苹果3的质量，第一阶段为苹果与果箱间的碰撞，果箱以a0的加速度撞向苹果1，假设碰撞后果箱的状态为静止，则苹果1受到的力为F1，发生碰撞后苹果1的加速度为a1，则

F1=m0a0

(8)

a1=F1/m1

(9)

第二阶段是苹果与苹果间的碰撞，苹果1以a1的加速度撞向苹果2和苹果3，苹果2和苹果3分别受到F2和F3的力，获得a2、a3的加速度，苹果1 的加速度则变为a4，忽略碰撞时的能量损失，由能量守恒定理有

(10)

假设，苹果的质量相等，则

(11)

a2和a3始终小于a1，F2和F3始终小于F1。果1在和果箱碰撞后可能会和多个果2接触发生碰撞，同样果2也会和多个果1发生碰撞，这会造成果2受力大于果1，但从整体来看，苹果与苹果碰撞受到的力小于苹果和果箱碰撞受力。所以苹果在运输过程的损伤主要发生在苹果和果箱碰撞这一阶段。

3.2 苹果与果箱间的碰撞

苹果与果箱碰撞，是整个碰撞过程中的第一阶段，在这一阶段，苹果受损严重。以所有与果箱接触的苹果为对象，研究不同时间内苹果综合受力最大值，如图7所示。

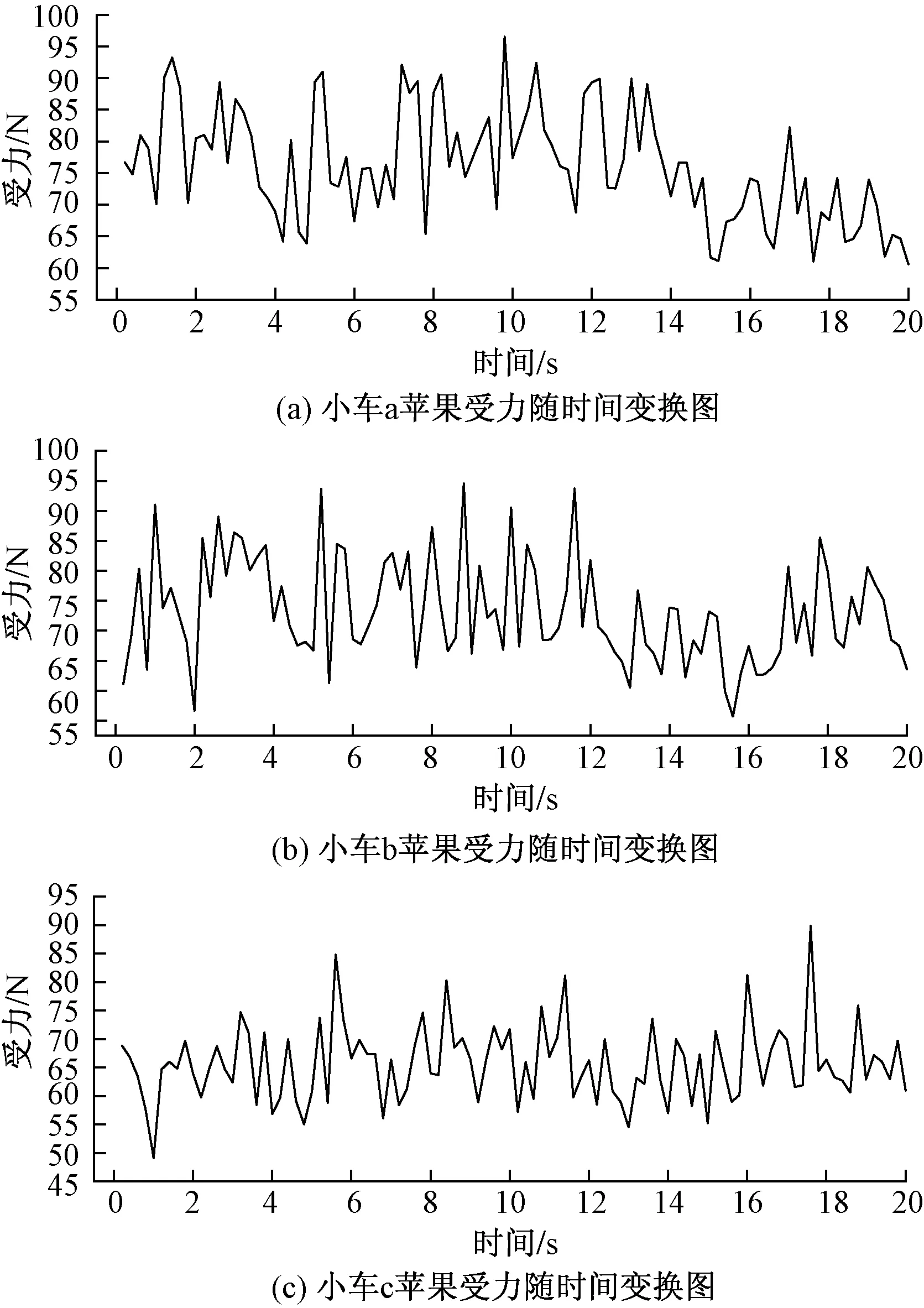
图7 苹果与果箱碰撞综合受力图

由图7可知，小车a、小车b和小车c中苹果与果箱碰撞综合受力峰值分别为97、94、90 N，小车a与小车b的苹果受力峰值大于小车c的受力峰值；小车a和小车b的苹果单位时间内综合受力最大值集中在60～90 N之间，小车c集中在55～75 N；小车c中苹果与果箱碰撞综合受力小于小车a和小车b。

在整个仿真过程中单个苹果可能会和果箱发生多次碰撞，每次碰撞受力也各不相同，选取其最大值进行分析，苹果与果箱碰撞受力状态分布如图8所示。

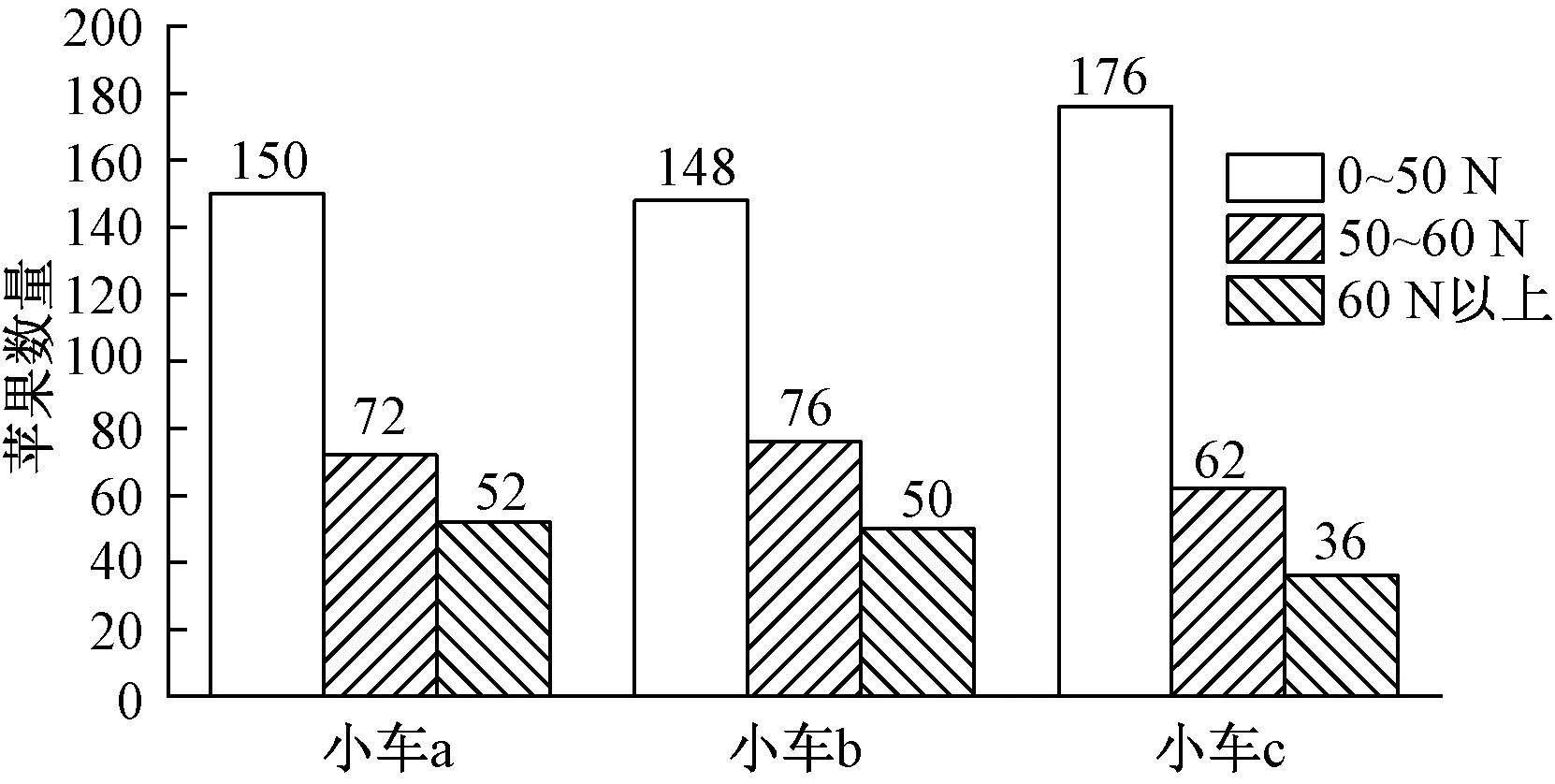
图8 苹果与果箱碰撞受力状态分布图

由图8可知，在整个仿真过程中，小车a和小车b运输的苹果在三个受力范围内的数量十分接近。小车c运输的苹果在受力0～50 N这个范围内的苹果数要大于小车a和小车b；在50～60 N这个范围的苹果数量略低与另外两组运输小车；在60 N以上这个范围的苹果数量为三组运输小车最小值，且与其他两组存在明显区别。

以60 N为苹果受损的阈值，将受力为50～60 N的苹果定义为潜在受损苹果，不同运输车中苹果与果箱碰撞损伤率和潜在损伤率如表3所示。

表3 不同运输小车苹果与果箱碰撞损伤率

小车a中苹果与小车b中苹果的损伤率分别为18.38%和18.97%，小车c中苹果的损伤率为13.14%；小车c相较于小车a与小车b损伤率下降了5个百分点左右；与此同时小车c的苹果潜在损伤率较另外两组降低了近4%。

3.3 苹果和苹果间的碰撞

苹果与苹果碰撞，是整个碰撞过程中的第二阶段，在这一阶段，苹果受损较为严重，单个苹果综合受力最大值如图9所示。

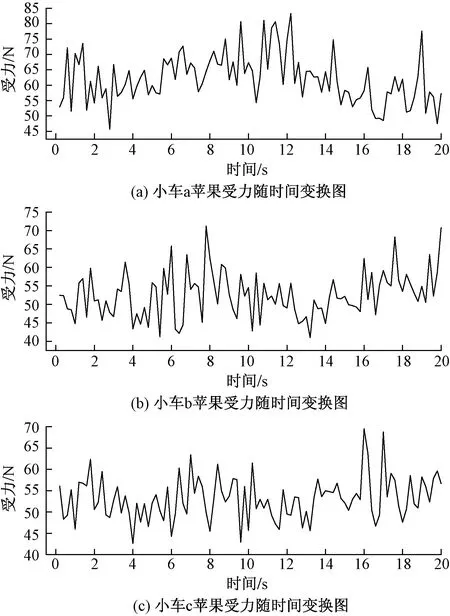
图9 苹果与苹果碰撞综合受力图

由图9可知，小车a、小车b和小车c在仿真运输过程中苹果与苹果碰撞受力峰值分别为83、72、69 N；小车a和小车b中苹果不同时间内综合受力最大值分布范围较为接近，都在45～85 N之间，小车a苹果受力主要分布在40～70 N之间；小车c中苹果受力峰值及分布范围均小于小车a和小车b。

小车c中苹果与苹果碰撞不同方向受力最大值分布如图10所示。

对比图10与图9(c)可知，小车c苹果在某一时间单向(x向或z向)的受力小于60 N，但综合受力大于60 N。在实际运输过程中苹果会受到多个方向的力，单个方向的力可能无法造成苹果的损伤，但综合受力可能超过苹果损伤阈值，造成苹果损伤。在结构设计时考虑多方向的减振以及在仿真时添加多方向的激励，有利于提高仿真的准确性。

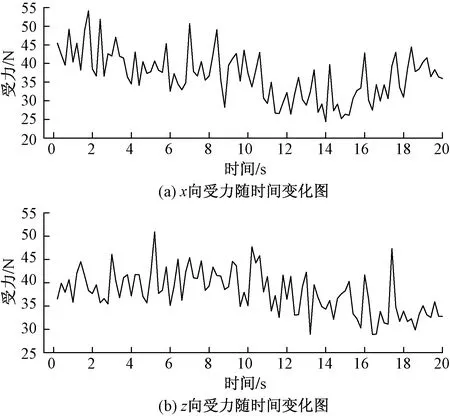
图10 小车c苹果不同方向受力图

采用不同减振结构，单个苹果在整个仿真过程中受力最大值分布如图11所示。

由图11可知，在整个仿真过程中，小车a与小车b受力超过60 N的苹果占总数的6%左右，小车c受力超过60 N的苹果占总数的3%，较小车a与b有显著的改良。受力为50～60 N的苹果可以被定义为潜在受损苹果，小车c的潜在受损苹果数同样小于小车a与小车b。

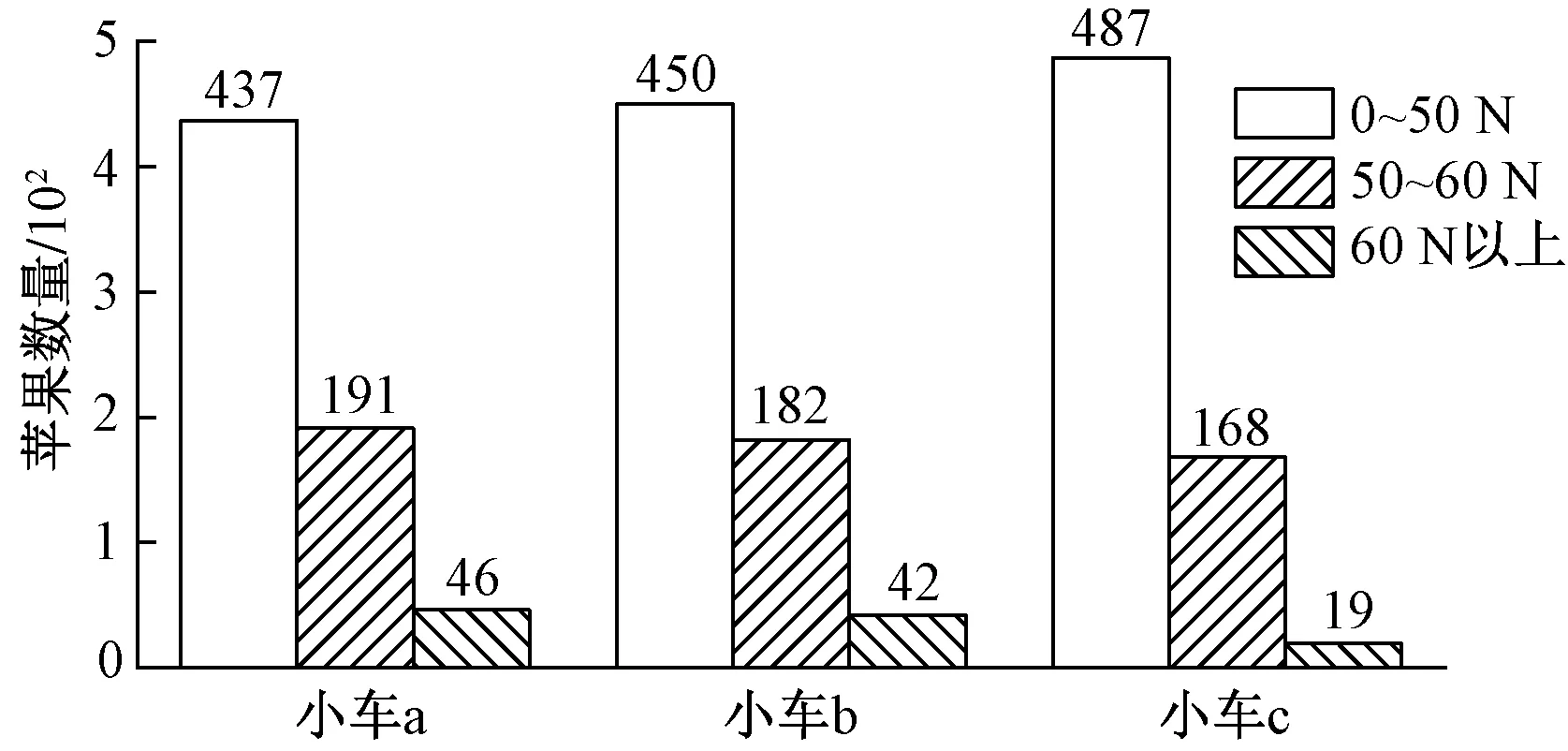
图11 不同结构单个苹果综合受力最大值分布

采用60 N作为苹果受损的阈值，不同减振结构下苹果损伤率如表4所示。

表4 苹果与苹果碰撞损伤率及潜在损伤率

小车a中苹果与小车b中苹果的损伤率分别为6.23%和6.82%，小车c中苹果的损伤率为2.82%，小车c相较于小车a与小车b苹果损伤率下降了3.5个百分点左右。小车c中苹果潜在损伤率同样低于其余两组，小车c的减振性能优于下次a与小车b，所以使用小车c运输苹果，可避免不必要的损失。苹果综合损伤率如表5所示。

表5 苹果综合损伤率

不同结构的综合损伤率不等于苹果与苹果间的碰撞损伤率与苹果与果箱间的碰撞损伤率之和。苹果与果箱碰撞损伤和苹果与苹果碰撞损伤存在交集，假设苹果a在与果箱碰撞时受力超过60 N，苹果a被定义为损伤，苹果a在与苹果的碰撞中受力也超过了60 N，那么苹果a被再次定义为损伤，如果把综合损伤率定义为第一阶段碰撞损伤率和第二阶段碰撞损伤率之和，这样会重复统计类似苹果a的苹果。

以苹果为例，小车c中果实的损伤率为6.23%相较于小车a的11.12%和小车b的10.83%，降低近5%；小车c果实潜在损伤率同样低于其余两组的潜在损伤率。小车c的减振性能优于小车a与小车b，使用小车c运输果实能够有效避免运输过程中果实与果实及果实与果箱碰撞而造成的果实损伤，降低果实损伤导致的经济损失。

4 结论

首先对苹果在丘陵果园内运输损伤原因进行分析；采用Hertz接触理论对运输过程中苹果受力进行理论分析；建立ADAMS动力学和EDEM离散元联合仿真模型，对采用三种不同悬架的果园运输车运输过程进行仿真。将整个碰撞过程分成两个阶段，第一阶段果箱和苹果碰撞，第二阶段苹果和苹果碰撞。对不同阶段的仿真结果进行分析，得到如下结论。

(1)第一阶段的苹果损伤率大于第二阶段的苹果损伤率，小车c在两个阶段苹果损伤率均低于其他两组运输车，分别降低近5%和3%。

(2)小车a、小车b、小车c中苹果综合损伤率分别为11.12%、10.83%、6.23%。小车c的果实损伤率较现有运输车(小车a和小车b)降低5%左右，优化效果明显。

这为水果运输机械设计和性能评价提供一定的参考，后续将对果园运输工况下水果的累积损伤做进一步研究。