基于LS-SVM的TBM掘进参数预测模型

张哲铭，李晓瑜，姬 建,2

(1.河海大学土木与交通学院，江苏 南京 210098； 2.河海大学岩土工程科学研究所，江苏 南京 210098)

随着我国掘进机技术的迅速发展，全断面隧道掘进机(tunnel boring machine，TBM)已经被广泛运用到铁路隧道、水利隧道以及采矿工程中[1]。但是地质情况多变性、岩-机相互作用机理复杂性对TBM掘进性能的干扰问题一直难以解决。目前主要依靠现场工程师和TBM司机的经验对掘进参数进行调节，但一旦遇到复杂地质条件，难以及时调整掘进方案，容易导致TBM卡机及严重的地质灾害。因此实现TBM安全高效掘进的首要任务是在掘进过程中根据不同地质条件等因素合理选择掘进参数[2]。如今工程建造的智能化以及大数据平台的建立使得TBM的安全高效掘进和智能控制显得越来越重要，TBM掘进参数的预测成为当前研究的一个热点。欧洲地下工程施工战略研究机构已经把“无人值守TBM掘进”作为2030年的远景目标[3]。

国内外众多学者主要采用传统方法、智能算法对TBM掘进参数进行预测，目前预测模型主要有单因素预测模型、综合预测模型(CSM模型和NTH模型)、岩体分类预测模型(QTBM模型)、概率模型、模糊神经网络模型、罗宾斯模型等[4]。Yagiz[5]通过引入脆性指数、节理间距、节理角度等岩体参数对CSM模型进行修正，实现了TBM推进速度的精准预测。挪威科技大学基于大量现场掘进试验数据提出了NTNU模型[6]，并预测了TBM的净推进速度。尽管传统方法的预测模型可解释性强，但其影响因素过多、建模过程复杂，具有很强的专业性，因此影响了其推广性。温森等[7]采用Monte Carlo-BP神经网络，以完整岩石的单轴抗压强度、巴西试验劈裂抗压强度等5个岩石性质参数作为输入参数预测TBM推进速度。Mahdevari等[8]在考虑了岩石性质与设备性能前提下，提出了一种基于支持向量机回归的TBM掘进参数预测模型，并将其成功应用于纽约市政供水隧道项目。基于智能算法的预测模型具有强大的表示能力，可以很好地预测参数总体趋势，但其容易受数据样本容量大小和数据质量的影响，从而降低预测模型的泛化能力。上述研究考虑了大量的微观力学因素和围岩特性因素，但在掘进参数优化预测分析、数据处理挖掘方面依然有所欠缺，实际施工过程中的作用并不明显。因此需要从TBM掘进参数的数据挖掘理论和方法等方面进行突破，提高掘进机的掘进性能，以期为掘进机的无人驾驶技术提供一定的理论支撑。

笔者基于吉林引松供水隧道工程，借助中铁装备TBM混合云管理平台，针对TBM施工现场掘进规律研究不足和传统分析方法在TBM掘进参数预测方面的局限性，将改进支持向量机——最小二乘支持向量机(least squares-support vector machine，LS-SVM)[9]应用于TBM掘进参数预测中，建立基于LS-SVM的TBM掘进参数预测模型(以下简称LS-SVM模型)。

1 LS-SVM原理

支持向量机理论(SVM)是20世纪90年代Suykens等[10]基于统计学习理论提出的一种新型的通用机器学习方法，具有良好的非线性映射和学习推广能力，正成为继神经网络之后的研究热点。 LS-SVM是SVM用于分类和回归分析的另一种替代形式，它将二次优化问题转化为线性方程组，因此比SVM具有更强的计算优势[11]。为得到最优解，LS-SVM将一定数量的样本随机分为训练集和测试集，训练集中的每个实例都包含一个目标值(输出变量)和若干属性(输入变量)。LS-SVM的目标是基于真实试验或数值模拟得到的训练数据，拟合得到一个代理模型来映射一组输入和输出之间的关系。

对于给定的训练集{(xi,yi)|i=1,2,…,N},xi∈Rn为输入变量，yi为输出变量，其中Rn为n维向量空间。为了描述LS-SVM的预测功能，优化问题公式为

(1)

s.t.yi(xi)=wTφ(xi)+b+ei

(2)

式中：J(w,e)——误差总和；w——可调整权重向量；ei——拟合误差向量e的元素；γ——正规化常数；b——偏差常量；φ(xi)——非线性映射函数。

为了求解上述优化问题，需要构造拉格朗日函数：

(3)

式中：αi——支持向量α的元素。

拉格朗日函数分别对w、b、ei、αi求一阶偏导数，并令其一阶偏导数等于0，即：

(4)

将式(4)转化为矩阵形式：

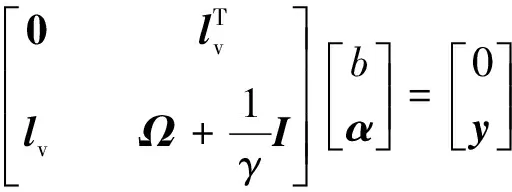
(5)

其中lv=(1,1,…,1)Ωij=φ(xi)Tφ(xj) (j=1,2,…,N)

映射函数φ(·)根据Mercer条件[12]可以通过核函数K(xi,xj)的方式体现：

K(xi,xj)=φ(xi)Tφ(xj)

(6)

求出α和b后，最终LS-SVM模型可以表示为

(7)

核函数中包含2个未知常数，即核常数σ和正规化常数γ，LS-SVM模型的求解直接依赖于它们。为了找到LS-SVM模型的最优解，通过网格搜索方法[13]反复调试模型确定这2个常数。此外，为了避免过度训练，通常采用基于训练数据集和验证数据集的交叉验证方法。由于LS-SVM模型参数较少，不存在陷入局部极小值的问题，因此计算量远小于神经网络方法。

2 实 例 验 证

2.1 工程概况

吉林省中部城市引松供水隧道工程，TBM四标始发里程71+476，结束里程51+705，共计长度19 771 m，其中钻爆段长度2 283 m，TBM掘进段长度17 488 m。TBM掘进时间共31个月，合928 d，扣除钻爆段、检修及不良地质停机时间，TBM有效掘进时间为728 d。施工主要穿越石灰岩和花岗岩两类地层。TBM主要技术参数：开挖直径8 030 mm，刀具数量56把，驱动功率3 500 kW，刀盘转速为0～3.97～7.6 r/min，最大推进速度120 mm/min，额定扭矩8 410 kN·m，脱困扭矩12 615 kN·m，最大推进力23 260 kN@35 MPa。

2.2 TBM掘进数据与主要参数

TBM在掘进过程中，每一个掘进循环都是一个动态过程，其走势大致相同，图1为某一个掘进循环。在空推段到接触岩壁瞬间，主控室振动感受强烈，TBM司机会瞬间降低推进速度，推进速度出现下降沿，此下降沿的终点为上升段的起始点；上升段，掘进机滚刀开始侵入岩体，各项掘进指标都急剧上升，并随着时间推移进入稳定段，稳定段各项掘进指标均趋于平稳；当一个循环结束，逐步停机。图1中上升段类似掘进试验，包含了丰富的岩-机信息，是岩体条件和刀盘掘进性能的综合反映；稳定段是TBM以安全、快速、高质量的稳定状态掘进的主要阶段，此时岩体条件是决定TBM掘进参数的关键因素。因此，可通过上升段掘进参数变化规律预测TBM稳定段掘进参数，优化并调整当前参数以达到TBM安全高效掘进的目的。

图1 TBM某一掘进循环的数据分段Fig.1 Data segmentation of a TBM tunneling cycle

掘进过程中，中铁装备TBM混合云管理平台将设备运行数据按秒采集，以天为储存单元，共获取有效数据40.8亿组，完整记录了设备在不同地层、不同操作工况下的实际表现。另外，地质情况、特殊地层、工序时间、刀具消耗、材料消耗等数据均由人工现场记录、整理所得。

总推力和推进速度是TBM最重要的运行参数，预测TBM运行参数以及在此运行参数下的掘进性能对于TBM选型设计、工程工期和成本预估具有重要意义；刀盘转速和刀盘扭矩是重要的控制参数，合适的控制参数对于安全高效运行，延长设备寿命，避免事故等具有重要意义。本文通过Python数据切割和Matlab数据处理将中铁装备TBM混合云管理平台3年来记录的数据降维并处理为17 863个样本，在这些样本中选取了上升段开始后1～30 s和稳定段的刀盘转速、刀盘扭矩、总推力、推进速度、贯入度。由于贯入度为推进速度与刀盘转速之比，故只选取刀盘转速、刀盘扭矩、总推力、推进速度4个参数分别进行建模，由上升段的参数预测稳定段的参数。

2.3 模型构建及预测步骤

根据第1节的原理，构建LS-SVM模型。具体步骤如下：(a)训练数据采用已有数据的80%，共14 290组；测试数据采用20%，共3 574组；(b)每个样本读取为30×4的矩阵形式，横向分别为刀盘转速、刀盘扭矩、总推力、推进速度，纵向为上升段开始前1～30 s；(c)将每个样本的120个元素作为输入，将稳定段的刀盘转速、刀盘扭矩、总推力、推进速度分别作为输出建立4个预测模型，进行稳定段参数的预测，得到4个参数的预测值；(d)运用已建立的4个预测模型进行测试数据的预测。

2.4 预测结果分析

2.4.1 预测值与真实值比较

按照第2.3节步骤建立LS-SVM模型，分别得到刀盘转速、刀盘扭矩、总推力、推进速度4个模型训练集和测试集的预测数据。本文采用决定系数(R2，也称拟合优度)评价模型预测效果，R2越接近于1，模型预测效果越优。为了更好地评价LS-SVM模型的预测性能，同时也采用极限学习机(extreme learning machine, ELM)[14]方法学习同样规模的样本并构建模型进行预测。

由于数据量过于庞大，为了更直观地展示模型的预测性能，结果以图2形式展示。由图2和表1可以看出LS-SVM模型对于刀盘转速和总推力预测的效果比较优异，不论是训练集还是测试集，R2基本都达到0.8及以上；刀盘扭矩和推进速度的预测效果相对较弱。这是因为刀盘转速和总推力为TBM掘进性能参数，在掘进过程中较为稳定，而刀盘扭矩和推进速度受外界岩体信息等因素影响较大[15]。同时LS-SVM模型得到的预测结果R2比ELM模型高出10%～20%，说明LS-SVM在参数预测性能方面有一定的优势。

图2 LS-SVM模型预测效果(14 290组训练样本)Fig.2 Prediction results of LS-SVM model (14 290 training data)

表1 决定系数比较

2.4.2 模型样本及精度分析

作为一种数据驱动模型，LS-SVM模型的预测精度很大程度上取决于训练样本的数量及质量，太少的训练数据会导致丢失的“支持”元素太多，而过多的训练数据会导致计算量增加从而降低最小二乘向量机的性能[16]，因此选取一个规模适中的训练数据量很有必要。另一方面，对于每个属性变量，需做到训练样本在其域内尽可能均匀分布，以表现其整体特征，而不仅仅是局部特征。本节从上述14 290组样本中均匀提取2 000组样本重新进行建模和预测，结果如图3所示。

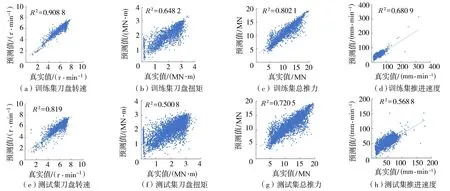
图3 LS-SVM模型预测效果(2 000组训练样本)Fig.3 Prediction results of LS-SVM model (2 000 training data)

从图2和图3可以看出2 000组训练样本的LS-SVM模型预测效果比14 290组样本的表现更为优异，刀盘转速、刀盘扭矩、总推力的R2都提升了3%～10%，推进速度的R2提升了59.1%。这说明训练样本规模对参数预测性能有较大影响，合适的训练样本数量才能使LS-SVM模型的预测性能达到最优。

2.4.3 核函数的选取

线性不可分的问题可以通过把样本值映射到更高维的特征空间或者无穷维解决。在特征空间中，求解线性可分情况下的分类问题时，需要计算样本内积，但是因为样本维数很高，容易造成“维数灾难”，所以引入了核函数[17]把高维向量内积问题转变成低维向量内积问题。3种常用的核函数分别为RBF核函数(式(8))、多项式核函数(式(9))、线性核函数(式(10))。采用上述3种核函数进行模型的训练与预测，预测结果的R2见表2。

表2 不同核函数的决定系数比较

K(xi,xj)=exp{-|xi-xj|2/σ2}

(8)

(9)

(10)

如表2所示，多项式核函数在训练集的表现最为优异，R2达到0.95以上，但在测试集中表现效果最差；相较于线性核函数，RBF核函数不管在训练集还是测试集，效果都较为优异。这是由于RBF核函数可以定义一个比线性核函数或多项式核函数更大的函数空间，故RBF核函数适合运用在TBM参数预测中。

2.4.4 交叉验证的影响

交叉验证的影响在LS-SVM优化中不可忽视。一般来说，交叉验证越多预测结果越好，但计算量会增加。10折交叉验证是最常见的，但交叉验证折数在TBM参数预测这样大规模数据训练预测中的影响尚未有文献明确描述。本文以刀盘转速为例，分别采用3折、5折、10折交叉验证训练不同规模大小的数据，结果如图4所示。

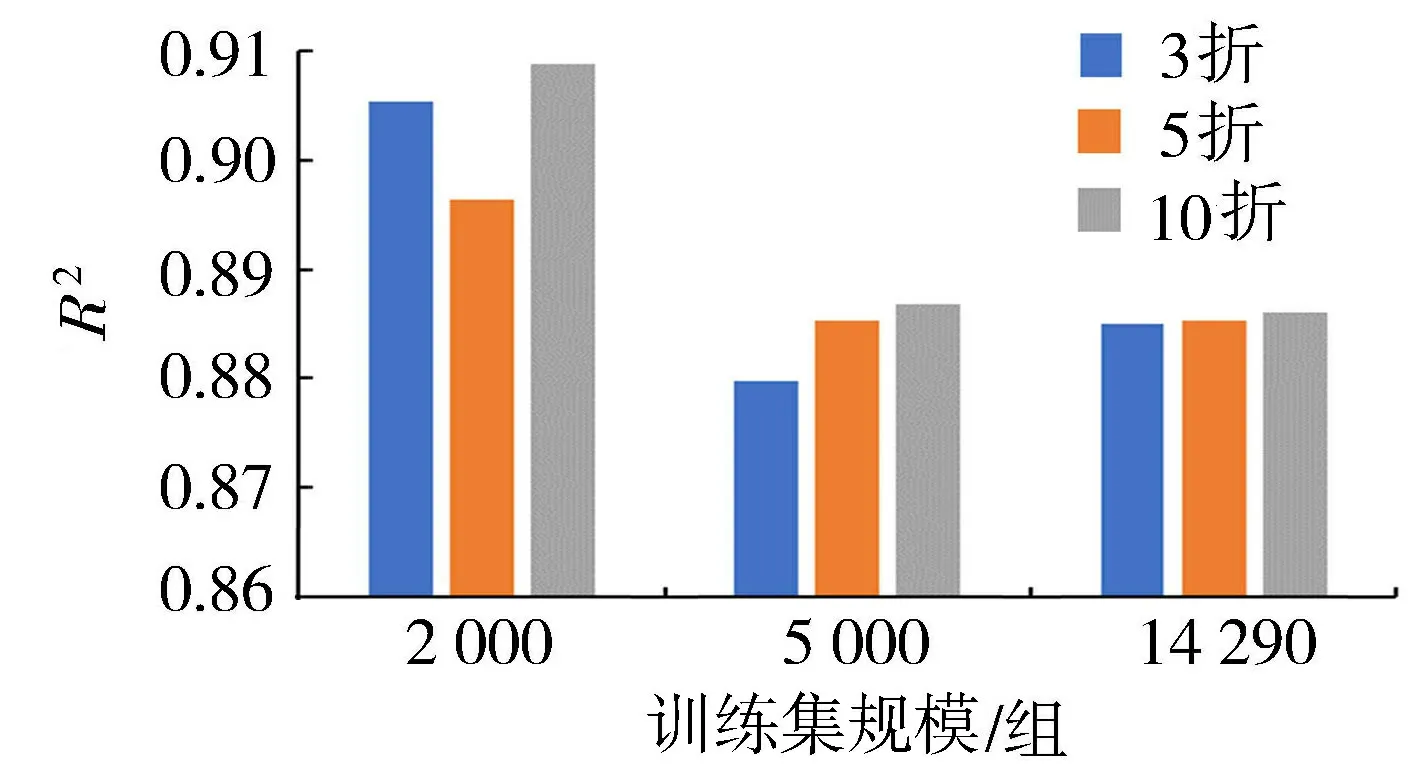
图4 不同交叉验证折数下刀盘 转速预测结果的决定系数Fig.4 Comparison of model evaluation parameter R2 of cutter torque speed for different cross-validation folds

图4表明，对于同一训练集规模，10折交叉验证得到预测结果R2高于3折和5折交叉验证；同时随着训练集规模的增大，刀盘转速预测结果的R2呈下降趋势，可以看出训练集为2 000组样本的预测效果最为理想，其预测结果的R2最大。所以选取代表整体数据特征的样本建立合适训练集规模的模型、选择合适的核函数比盲目增加交叉验证折数更为关键。

2.4.5 输入参数选取

根据上升段各参数数据预测稳定段的司机操作参数，属于对司机驾驶习惯的行为建模。考虑到刀盘转速和推进速度属于掘进控制参数，刀盘扭矩和总推力属于设备性能参数，如果模型预测的刀盘转速和推进速度与司机实际的操作参数不一致，必会影响模型对刀盘扭矩和总推力的预测。所以当模型预测结果与司机操作参数有较高的一致性性时，应继续完善模型对设备性能参数预测的准确性。

本节在第2.3节模型基础上将稳定段的刀盘转速和推进速度的均值也作为模型的输入参数，按照第2.3节步骤重新建立模型并进行预测，结果如图5所示。

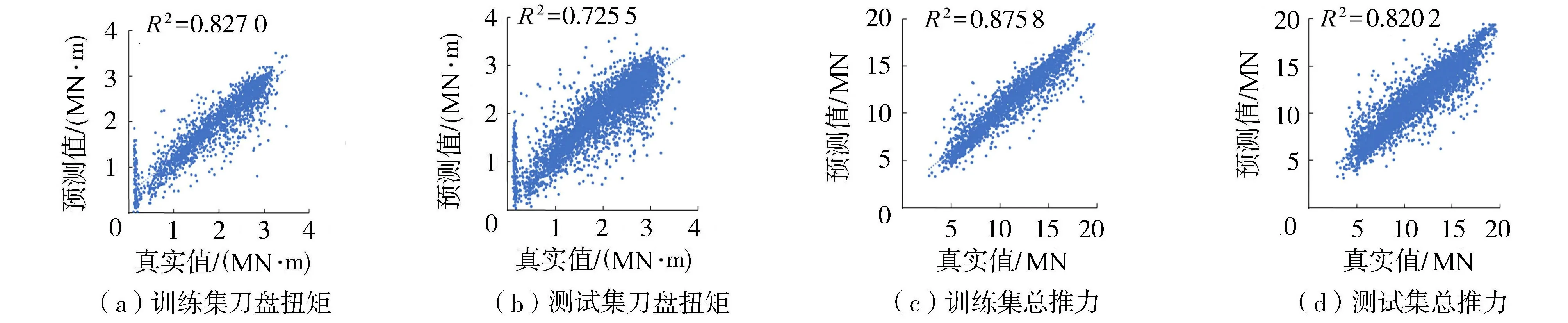
图5 增加稳定段刀盘转速和推进速度的LS-SVM模型预测效果(2 000组训练样本)Fig.5 Model prediction results of LS-SVM model after adding cutber rotation speed and propulsion speed of stable section (2 000 training data)

由图5可以看出将稳定段刀盘转速和推进速度添加进输入参数的LS-SVM模型预测效果相较于原模型在刀盘扭矩和总推力预测的表现有了明显的提升。经计算，刀盘扭矩训练集和测试集的R2为0.827 0和0.725 5，分别提高了27.6%和44.9%,总推力训练集和测试集的R2为0.875 8和0.820 2，分别提高了2.3%和21.6%。这说明训练参数的选取对模型预测性能有较大的影响，合适的训练参数才能使LS-SVM模型的性能达到最优[18]。LS-SVM模型的效果主要依赖于大数据本身提供的隐含信息，相较于第2.3节模型，该模型考虑了更多稳定段的信息，增加了模型的输入参数，进而改善了模型的预测能力。

3 结 论

a.TBM掘进性能预测不仅可以从围岩条件等外部因素的角度进行考虑，也可以从TBM掘进过程中参数的数据挖掘理论和方法进行突破，借助LS-SVM出色的学习能力和推广性能，从有限的TBM性能参数深度挖掘掘进过程中的规律，提高掘进机的掘进性能，为以后掘进机的无人驾驶技术提供一定的理论支撑。

b.依托于吉林引松工程中的TBM数据，筛选出刀盘转速、刀盘扭矩、总推力、推进速度4个参数并建立基于LS-SVM的预测模型，能够从上升段前30 s的数据预测稳定段的均值且预测效果理想，尤其是刀盘转速和总推力预测结果的R2达到0.908 8和0.802 1，与ELM神经网络方法相比具有更高的精度和更强的鲁棒性，因此所得的预测结果具有更高的参考价值与工程意义。

c.在建立LS-SVM模型时，选择的训练样本要尽可能在其域内均匀分布，针对不同问题应选用合适规模大小的训练数据、核函数以及交叉验证折数，这样才能得到最优的模型预测性能。

d.在TBM性能参数(刀盘扭矩、总推力)预测模型输入参数中增加设备性能参数(刀盘转速、推进速度)，刀盘扭矩预测结果的R2提高了44.9%，总推力预测结果的R2提高了21.6%。LS-SVM模型的预测效果主要依赖于输入参数本身提供的隐含信息。