基于ADAMS 的管道外壁行走装置的设计与仿真
孙晓东
淮南联合大学 机电系,安徽 淮南 232038
针对现代工业现场应用,设计出了一种针对圆形直管道的管道外壁行走装置。该平台可以在管道外壁上自行走,协同搭载的各种检测、喷涂等装置,完成直管管道的检测维护等各种工程应用。总体结构如图1 所示。

图1 管道外壁行走装置三维实体模型
1 多体系统动力学概述
计算动力学是一门综合了刚性体与柔性体的运动学与动力学、有限单元法、计算方法以及优化和控制理论的综合性学科[1],多体系统动力学是计算动力学的一个重要分支。计算多体动力学的核心问题是建模和求解,对其系统研究开始于20 世纪60 年代,稍晚于计算固体力学,早期的研究对象是多刚体系统。
多体系统动力学的建模方法主要基于以下几类基本原理和方法:Newton-Euler 向量力学方法、d’Alembert 原理(或 Jourdain 原理、Lagrange 方法)出发导出的分析力学方法、基于Gauss 原理等极小值性质的机制原理以及传递矩阵方法等。
随着实际工程应用的需要,计算多体系统动力学在50 多年的时间里取得了令人瞩目的成果,简化了工程问题的处理和测试。目前各科研机构研发了多种多体动力学CAE 软件,来满足实际工程应用 的 需 要 ,Msc.ADAMS、SIMPACK、DADS 和RecurDyn 是比较知名的。
2 管道外壁行走装置几何模型的建立
ADAMS 是 由 美 国 MDI 公 司 (Mechanical Dynamics Inc.)开发的虚拟样机分析软件,现已被美国MSC 收购更名为MSC/ADAMS,是当今应用最广泛的虚拟样机分析软件之一。
应用机械系统动力学分析软件ADAMS(Automatic Dynamic Analysis of Mechanical Systems)[2][3]对管道爬行装置进行运动学仿真。把管道爬行装置模型进行适当简化导入到ADAMS 中,布置方式为管道轴线沿z 轴方向,给不同的零部件设置材料属性,整个装置在ADAMS 中的模型如图2 所示。

图2 行走装置导入ADAMS 的几何模型
在ADAMS 中将对相应的零部件进行约束,具体为:将支架与管道之间、支架与大地之间建立固定约束,驱动轮和支撑轮分别与管道建立接触约束,将各轮与其支架之间建立转动副,各滚轮支架与固定到圆盘上的支撑座之间建立移动副,并且在其间建立弹簧力元。
将所有的零部件当做刚体考虑,各相邻刚体之间通过铰建立起前面所述的相对运动关系,进而组成整个系统的运动学约束方程组,再给以驱动约束方程即可对该多刚体系统进行运动学求解。
3 管道外壁行走装置运动学仿真
管道外壁行走装置在ADAMS 中进行运动学求解之后的位移、速度和加速度特性如图4 和图5 所示,图4 为启动该装置时的运动学特性曲线。
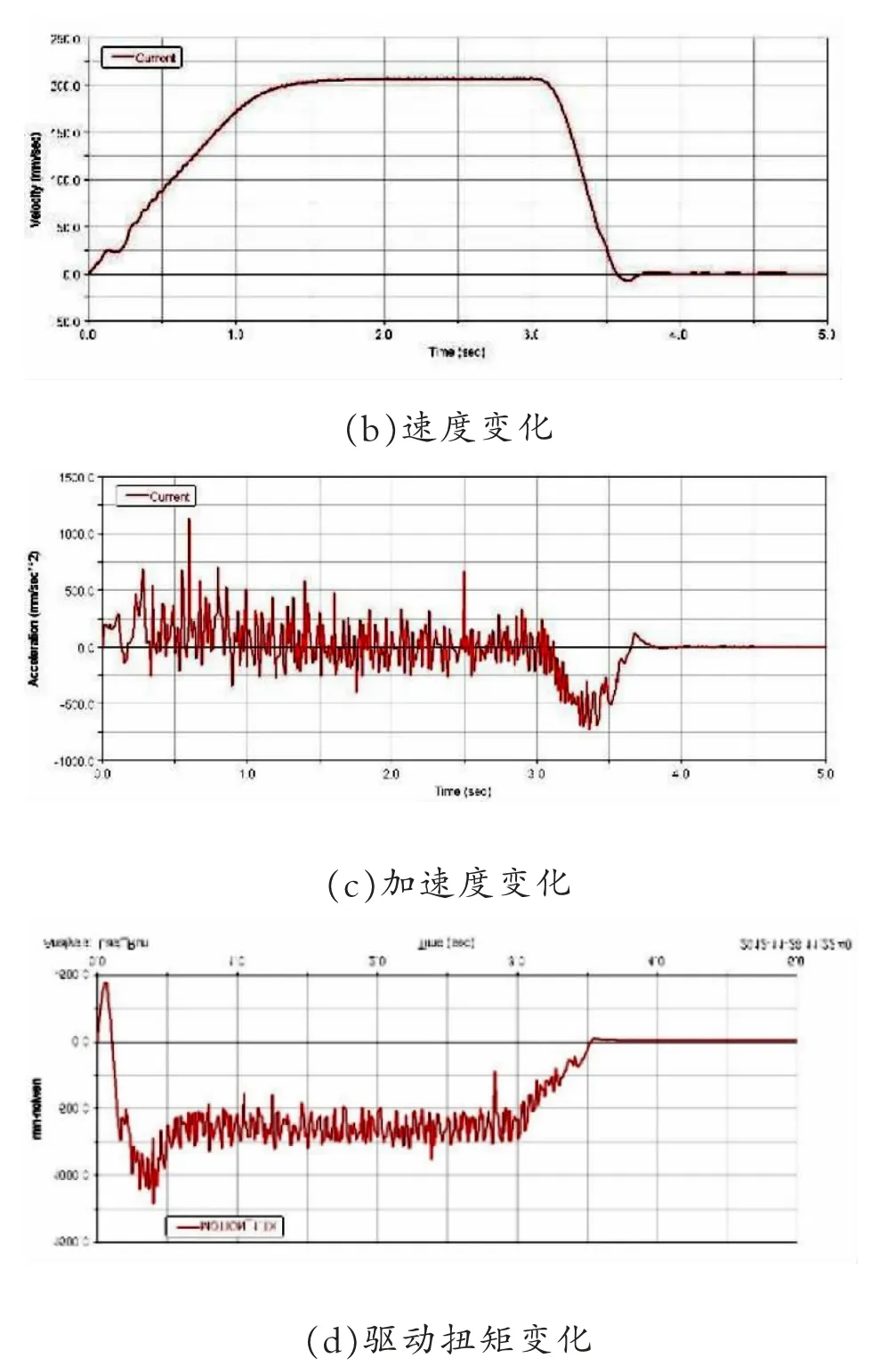
图4 行走装置停止时运动特性

由图3 可知在管道外壁行走装置的启动时,在开始一段时间内,位移、速度和加速度曲线都有一个过渡区域。

图3 行走装置启动时运动特性
由图(a)可知在这一过渡区域内,该装置在管道上基本保持不动。由图可见在0~0.5s 这一段时间内,位移曲线基本保持水平,随后的一段时间随着速度趋于稳定位移开始缓缓变化,从1s 时刻开始位移曲线呈线性规律变化。
由图(b)可知在启动装置的初始时刻,速度曲线有一缓慢变化过程,在0.2s 时刻速度波动比较大,从1.2s 开始,速度曲线开始趋于平稳,该装置开始稳定运动。
由图(c)可知,加速度曲线在整个过程中始终以0 为中心呈无规律震荡,在0~0.7s 这一段时间内,加速度曲线震荡幅度比较大,最大加速度达到1.15m/s2,如果结构设计不合理会造成工作装置的损坏;从1.5s 之后,加速度曲线震荡幅值呈逐渐减小趋势,随着工作时间的增加,加速度值会逐渐减小为零。
由图(d)可知,施加到驱动轮上的扭矩开始有波动,但是稳定运转后保持在一定范围内周期性波动,波动平均值约为0.7N·m。
管道外壁行走装置停止时的运动学特性曲线如图5 所示。
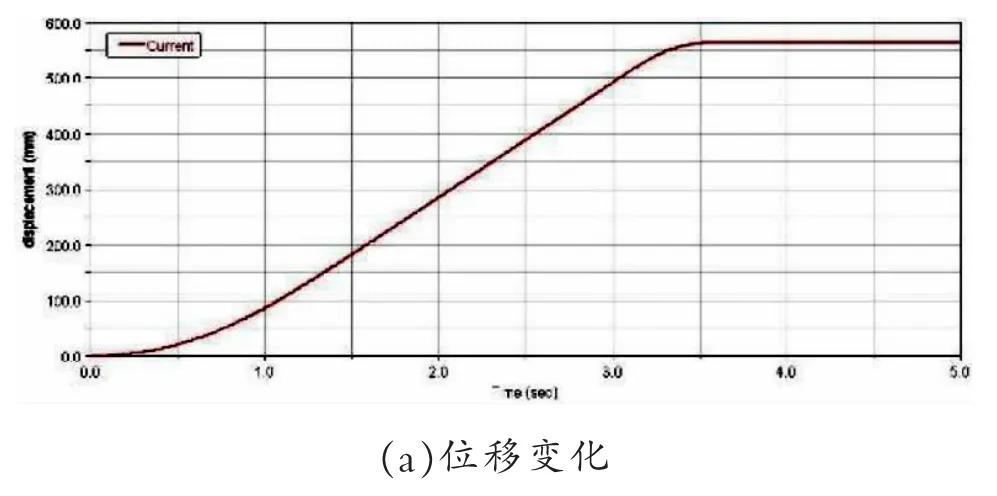
图4 所示为在3s 时刻让该装置停止运动,可知在发出停止指令后,该装置的运动特性变化规律与开始运动时相反。由(a)可知,在发出停止指令后该装置的位移曲线的斜率基本不变,随着速度逐渐减小位移曲线趋于一个稳定值,即装置停止;由(b)可见,速度曲线在逐渐减小过程中有波动,并且在速度达到零的时刻波动较大;由(c)可知,在发出停止指令后,加速度曲线呈无规律的震荡,总体趋势为加速度大小随时间的增加而逐渐减小,最后保持为零。
管道外壁行走装置在运动过程中的速度和加速度波动是由于结构件弹簧引起,因此在实际应用中要选用刚度比较大的弹簧,以提高装置的固有频率[6],同时驱动轮和支撑轮不能太硬,应该偏软让其在行走过程中吸收装置的运动波动,让装置在行走过程中保持良好的稳定性和安全性。
4 结语
通过基于ADAMS 的运动学仿真,对管道外壁行走装置的运动情况有了较为直观的反映,为下一步管道外壁行走装置整体结构设计的优化提供了相关依据。

