量子假设检验互信息

张淑仪 席政军

(陕西师范大学计算机科学学院 西安 710062)

在经典信息论中，Shannon互信息是刻画两个随机变量相互之间独立程度的度量，在信道编码中有很重要的应用且给出了信道容量[1].在量子信息论中，通过von Neumann熵形式给出了互信息的基本定义(与Shannon互信息对应，本文称作von Neumann互信息，通常也称作量子互信息[2]).在量子信息处理中，von Neumann互信息可以描述两体量子态上的全部关联[3]，也用于量子信道容量的刻画[4-5]，并在量子资源理论中有非常好的应用[6].von Neumann互信息可以由量子相对熵给出4种等价的定义.在量子信道容量的研究中，结合信道的n次重复使用(独立同分布)基于量子互信息来描述信道容量.而实际中较大量子系统上的操作难以实现且独立同分布的量子态难以制备等限制，一般考虑带有误差的有限情形或者one-shot情形(也就是n=1的情形).在one-shot量子信息论中，涉及到带参数的熵，量子假设检验相对熵就是非常重要的一类带参数的熵.量子假设检验相对熵来自于量子假设检验，量子假设检验类似于2个量子态的区分问题.量子假设检验是量子信息处理中的基本问题[7-8]，已得到很好的发展和应用[9-18].

文献[19]在前人工作的基础上集中讨论了量子假设检验相对熵，较为系统地研究了其性质，给出了在one-shot经典-量子信道容量中的应用.文献[20]给出了与文献[19]等价的另一个量子假设检验相对熵，得到了与其他广义熵之间的关系.文献[21]基于量子假设检验相对熵[19]定义了量子假设检验条件熵，刻画了具有量子边信息的数据压缩，得到了最小压缩长度的上下界.该文献也给出了量子假设检验相对熵和其他相对熵之间的一些关系.在量子假设检验相对熵的研究相对成熟的情形下，一个自然的问题是：用量子假设检验相对熵给出量子版本互信息的定义是否等价？如果不等价，是否存在序关系？本文将采用文献[19]中关于量子假设检验相对熵的定义，较为系统地研究其性质，并讨论与其他相对熵之间的关系.在Shannon互信息中，由于贝叶斯概率，容易得到条件熵和互信息的链式法则，但是目前还不清楚量子假设检验相对熵版本的互信息是否存在链式法则。本文将重点研究基于量子假设检验相对熵的互信息定义及其相应的性质.

1 相关基础知识

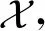
本文均使用以2为底的对数.若2个随机变量(X,Y)服从联合分布pxy，则Shannon联合熵定义为

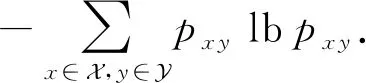
可以定义一个随机变量在给定另一随机变量下的条件熵，即

结合贝叶斯概率公式pxy=pxpy|x，得到联合熵和条件熵的链式法则，即

H(X,Y)=H(X)+H(Y|X).

(1)

对于同一字符集上的2个概率密度函数为px和qx，它们的相对熵定义为

(2)

I(X;Y)=D(pxy‖pxpy).

(3)

Shannon互信息刻画一个随机变量包含另一个随机变量的信息量，也描述已知另一随机变量所含有的信息量下原随机变量不确定度的减少量.结合Shannon熵的定义，Shannon互信息表示为

I(X;Y)=D(pxy‖pxpy)=
H(X)+H(Y)-H(X,Y)=
H(X)-H(X|Y)=
H(Y)-H(Y|X).

(4)

这里，I(X;Y)=H(X)-H(X|Y)和I(X;Y)=H(Y)-H(Y|X)这2个等式是双随机变量互信息的链式法则.

因为量子力学中并没有与在不同时间变量的2个变量的联合概率分布类似的概念[2-3]，从而对于两体量子态ρAB，并没有类似于pxy=pxpy|x的量子态表示形式，即ρAB≠ρA⊗ρB|A，其中ρA=trB(ρA)是约化密度算子，类似于边际概率分布.算子ρB|A并不是条件量子态，甚至不是量子态.因此，没有类似于Shannon条件熵的量子条件熵的直接定义.结合链式法则(1)，对于任意的两体量子态ρAB，基于子系统B的von Neumann条件熵定义为

S(A|B)=S(ρAB)-S(ρB).

(5)

显然，量子信息论中的von Neumann条件熵只是在形式上类似于经典信息论中的Shannon条件熵，在本质上它们之间有很大的区别，比如：当两体量子态为纠缠态时，S(A|B)<0.这说明von Neumann条件熵可以为负.von Neumann互信息定义为

I(A:B)=S(ρA)+S(ρB)-S(ρAB).

(6)

von Neumann条件熵和互信息在形式上都与Shannon条件熵和互信息保持一致.特别地，von Neumann互信息也有等式组(4)表示，具体讨论在第3节.

2 量子假设检验相对熵

量子假设检验问题涉及2个假设：

1)零假设(null hypothesis)H0:ρ⊗n，

2)备则假设(alternative hypothesis)H1:σ⊗n，

其中ρ⊗n=ρ⊗…⊗ρ和σ⊗n=σ⊗…⊗σ表示量子态的n次独立同分布(independent and identically distributed,i.i.d.)的拷贝态.需要解决的问题是基于量子测量结果确定哪一个假设是真的.量子测量由一个POVM(positive operator valued measure,POVM)来描述.本文仅考虑二值的POVM，相应的测量算子元为Mn和In-Mn，分别对应假设H0和H1的接受，从而产生2类误差概率：

αn(Mn)=tr((In-Mn)ρ⊗n),
βn(Mn)=tr(Mnσ⊗n),

其中,α(M)是当假设H0为真时接受假设H1的概率，β(M)是当假设H1为真时接受H0的概率.类似于经典假设检验问题，通常希望同时最小化这2类概率，但是它们之间存在均衡关系.一般情况下，约束其中一个误差概率而对另一个进行最小化.若第1类误差概率被限制在很小的参数ε∈(0,1)内，讨论第2类误差概率的最小化，量子Stein’s引理给出了渐近情形下关于误差概率的最佳可达误差指数[8-9]，即

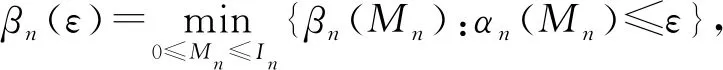
在非渐近情形下，对第1类误差概率限制下第2类误差概率的变化趋势是由量子假设检验相对熵来描述的.本文后面的讨论仅考虑单次拷贝的情形，且采用文献[19]中量子假设检验相对熵的定义.

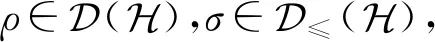
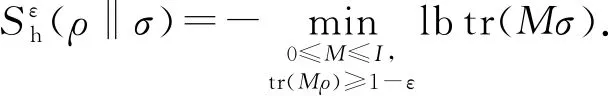
(7)

(8)

类似于von Neumann熵，该量化可以看做是量子假设检验熵.

量子假设检验相对熵满足数据处理不等式，也就是量子操作不会引起量子假设检验相对熵增加[19,22]，即对于任意的量子操作Λ都有

进一步地，如果考虑n次独立同分布的情形，当n充分大时，量子假设检验相对熵等于量子相对熵[18]，也就是渐近均分性(asymptotic equipartition property,AEP)，即

(9)

结合文献[20]的方法，基于定义1，使用von Neumann相对熵容易给出量子假设检验相对熵的一个上界，即

(10)

其中Hb(ε)=-εlb(ε)-(1-ε)lb(1-ε)为二元Shannon熵.

量子假设检验相对熵依赖于参数ε，量子态的ε-邻域发生变化，有可能导致量子假设检验相对熵发生变化.通过简单的计算可得性质1～4.

性质1.

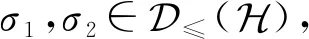
(11)

b.设ε1,ε2∈[0,1]，且ε1<ε2，有

(12)

该结果的详细证明见文献[22]不等式(11)表明：随着备择假设的增强，第2类误差概率变大.而不等式(12)表明：误差参数的越小限制，第2类误差概率反而变大.性质1给出了备择假设的变化引起的第2类误差概率的变化，结合文献[20]的结果，容易给出零假设的微小变化和参数变化共同引起第2类误差概率的变化情形.

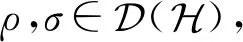
(13)

及

(14)

其中，δ∈(0,1-ε).

从定义1可知，量子假设检验相对熵本质上就是一个期望值，通过零假设的一些特定限制，可以直接估算量子假设检验相对熵的界.文献[23]首先给出了这方面的讨论.

性质3.设ρ为任意满秩态，σ为任意量子态，且0≤ε<λmin(ρ)，有

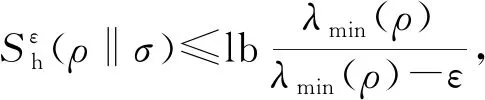
(15)

其中，λmin(ρ)是量子态ρ的最小特征值.

性质3仅是针对零假设为满秩态的情形，性质4给出一般量子态的情形.

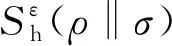
(16)

其中，λi(ρ)为ρ的特征值.

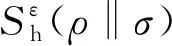
结合不等式tr(Mρ)≥1-ε，有

从而可得

则可以得到

从而命题得证.

证毕.

3 量子假设检验条件熵和互信息

在经典信息论中，对于联合概率分布，依赖于贝叶斯概率，得到条件熵等于联合熵与其中一个边际分布熵的差，也就是条件熵链式法则(1).在量子信息论中，并不存在条件量子态，从而不能直接推广经典条件熵的定义.如果考虑条件量子态，只能基于某一个子系统上的测量获得另一个子系统上的量子态.但是两体量子态的局部进行测量后整体量子态会发生改变，测量前后的状态可能并不相同.依赖于测量得到的条件量子熵一般并不等于von Neumann条件熵(5).研究发现它们的差正好能刻画复合量子系统上子系统之间的非经典关联[3].本节重点讨论von Neumann条件熵的形式，不涉及测量.

量子条件熵可以通过量子相对熵来表示[5,21].对于两体量子态ρAB和次归一化态IA⊗σB，它们的von Neumann相对熵为

S(ρAB‖IA⊗σB)=
-S(ρAB)-tr[ρABlb(IA⊗σB)]=
-S(ρAB)+S(ρB)+S(ρB‖σB).

(17)

由于本文采用次归一化态，从而von Neumann条件熵的相对熵表示与文献[1]的表述略有不一致.以该表示为标准形式，可以方便讨论量子假设检验相对熵性质的条件熵[19-22].

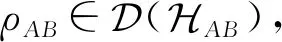
(18)

从定义2易得最优化的过程并没有一个精确解，即

根据Schatten ∞-范数的半正定程序[20,22]，量子假设检验条件熵也可以表示为

(19)

其中，MB=trAMAB.显然，并不能从等式(19)直接得到量子假设检验条件熵的精确解，这与von Neumann条件熵并不一致.但是对于等式(19)继续使用半正定程序易得到量子假设检验条件熵的许多性质以及和其他量化的关系，比如：数据处理不等式.该不等式的成立直接导致增加条件减小熵的结果.特别地，量子假设检验条件熵并没有类似于Shannon条件熵的链式法则(1).

在量子信息论中，对量子系统上的状态进行测量后会发生变化，测量前后的状态无法保持一致.因此无测量的von Neumann互信息是Shannon互信息形式上的直接推广.von Neumann互信息只是在形式上保持了Shannon互信息等价形式的一种，但在本质还是有所不同的.结合量子相对熵可以给出von Neumann互信息的4种等价形式，有

(20)

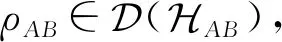
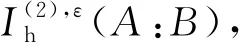
进而有

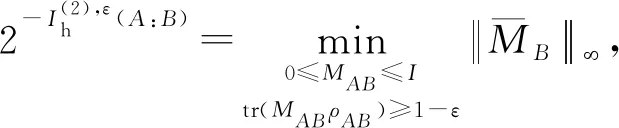
(21)

原问题

s.t.0≤MAB≤IAB

tr(MABρAB)≥1-ε

对偶问题

max(1-ε)η-tr(NAB)
s.t.ηρAB≤NAB+ρA⊗σB
NAB≥0,η≥0
σB≥0,tr(σB)≤1

.

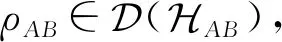
(22)

从而命题得证.

证毕.

由于量子假设检验互信息与误差参数有关，结合量子假设检验相对熵性质1直接可得量子假设检验互信息关于参数的序关系.对于0≤ε<ε′≤1，有

在三体量子系统中，对于von Neumann互信息中，丢弃一个子系统，互信息会减少.下面的结果证明量子假设检验相对熵的互信息也具有类似的性质.

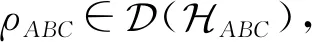
(23)

性质6的证明与性质5类似.特别地，当εA和εB均为恒等映射时，可得

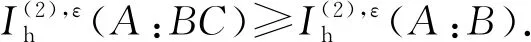
(24)

该关系说明丢弃子系统减少量子假设检验互信息.

经典-量子态在具有量子边信息的信源编码中有非常重要的应用，也对应于经典-信道编码.同时，在考虑基于测量的量子条件熵时，经典-量子态仅拥有经典关联.结合量子假设检验条件熵，下面讨论三体经典-量子态的情形.

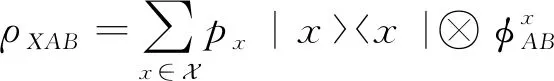
其中，dX是经典系统X的维数.

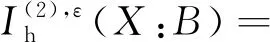
进而可得

类似地可以给出经典-量子态的量子假设检验条件熵的上下界，即

其中，c=|supp{px}|表示概率分布px的支集维数.

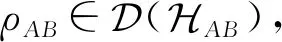
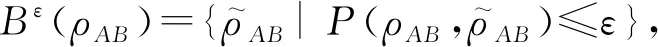
下面的结果给出量子假设检验互信息与量子最大互信息之间的关系.

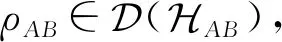
结合文献[20-21]中结果，使用本文量子假设检验相对熵的定义，通过基本的代数运算可以完成证明.与之类似的结果，结合不等式(10)，下面的结果给出量子假设检验互信息和von Neumann互信息的关系，即

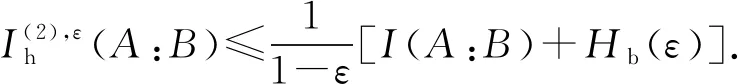
(25)

根据量子条件熵和量子互信息可以由量子相对熵表示，可知量子条件熵与量子互信息有量子互信息的链式关系，即

I(A:B)=S(ρA)+S(ρB)-S(ρAB)=
S(ρB)-S(B|A)=S(ρA)-S(A|B).

(26)

一般情况下，基于其他熵度量定义的互信息并不一定有等式(26)成立[20-21,24-25].下面讨论量子假设检验互信息的链式关系.首先基于量子假设检验相对熵定义单系统上量子假设检验最大熵.

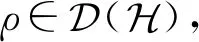
(27)

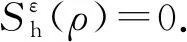
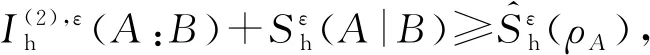
(28)

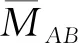
最后通过简单的代数运算，进而完成命题的证明.

证毕.

在该命题的证明过程中，得到了带限制的量子假设检验熵，该熵的测量算子依赖于条件熵的最佳测量，显然易得

另外，该命题仅给出了一个下界，但上界的证明目前还是一个开放的问题.虽然能给出互信息和条件熵的上下界，但是难以给出一个紧凑的链式关系.

4 总 结

在量子信息论中，基于von Neumann熵，可以得到类似于经典信息论中Shannon熵的好多有用量化和关系，在量子信息处理中有非常重要的应用.存在一些其他的熵在量子信息中的推广，但并不像von Neumann熵具有良好的性质或者关系，可关键是这些熵在one-shot量子信息论中有非常好的应用，比如假设检验相对熵.我们详细介绍了量子假设检验相对熵及其相关性质，并得到了新的上界.然后基于量子假设检验相对熵讨论了条件熵，得到量子假设检验相对熵形式的条件熵并没有类似Shannon熵或von Neumann熵的链式关系，这是由于假设检验相对熵或者新定义的最大熵都依赖于最优化.由于纠缠的存在同时并不存在量子版本的贝叶斯公式.对于量子假设检验相对熵，我们给出了4种不完全等价的互信息定义.结合在信息处理中常用的条件熵，主要讨论了其中一类互信息，得到了一些有意思的性质，并给出了和其他互信息之间的关系.给出了经典-量子态的量子假设检验互信息的上下界，得到了量子假设检验互信息类似于Shannon熵或von Neumann熵的互信息链式关系.