基于LSTM模型的国民经济GDP增长预测建模研究
朱青 周石鹏

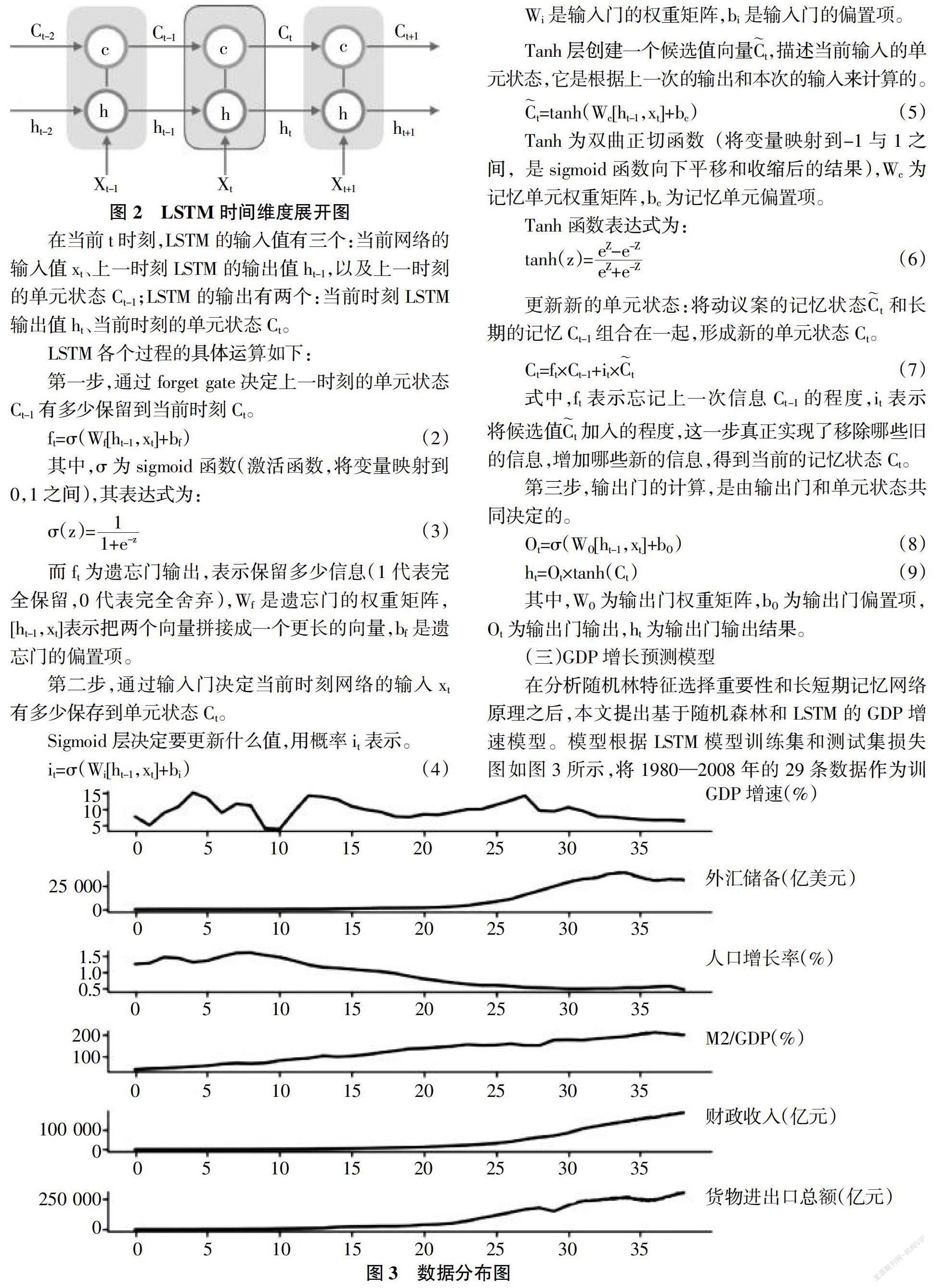
摘 要:传统时间序列方法在预测模型中要求时序数据稳定,但对复杂的非线性系统拟合能力较差,但GDP增长的预测精度不够准确。为了提高GDP增长的预测精度,首先利用机器学习算法Random Forest对影响GDP增长的变量进行重要性排序,选取重要变量,之后运用深度学习中的LSTM神经网络对GDP增长进行预测分析,并将预测结果与传统时序型ARIMA及GARCH模型进行比较。实验结果表明,基于递归神经网络的LSTM模型能较准确地反映我国GDP增长的变化规律。因此,LSTM模型在宏观经济预测中具有较高的应用价值。
关键词:GDP增长预测;LSTM;特征选择;随机森林
中图分类号:F12 文献标志码:A 文章编号:1673-291X(2021)19-0005-05
引言
近几年,全球经济和贸易增长逐渐放缓。国际环境复杂多变,贸易壁垒不断增加,世界经济面临增长乏力的局面。中国经济正在由高速增长阶段转向高质量发展。受全球经济放缓和中美贸易摩擦不确定的影响,经济运行总体平稳,GDP增速放缓。GDP增速反映经济发展趋势,与人民的生活水平息息相关。中国国家统计局数据显示,中国经济经过多年的高速增长后,2015年GDP增速为6.9%,2016—2018年的增速分别为6.7%,6.8%和6.6%。2019年6.1%的GDP增速是近年来最大的一次经济增速下降。能够精准预测GDP增速,对宏观经济目标的可行性和有效性的分析具有重要影响。
随着经济学的发展,出现了大量的经济预测方法,这些模型主要分为两类:一类是基于时序的外推法,比如移动算数平均法,指数滑动平均法;第二类是基于变量因果关系的因果法,比如回归分析法、计量经济学方法。但总的来看,经济预测工作进展并不顺利,主要体现在预测精度不尽如人意,随着机器学习和深度学习的发展,模型对复杂系统的拟合越来越好。
本文主要的尝试是:提出一种基于随机森林和LSTM的预测模型,构建多层神经网络更好地拟合宏观经济中的非线性关系和时序关系。
一、相关研究综述
目前,国内外对宏观经济预测的研究主要分为以下几类:首先是基于传统的时间序列预测模型。李瑞阁、黄佳艳(2018)利用ARIMA乘积模型对国民经济GDP进行预测研究,表明所选模型能较准确地反映我国季度GDP的变化规律[1];李娜等(2013)利用选定的最优ARIMA模型对我国GDP的增长模型进行预测,并阐明了模型的优良性和稳定性,但由于传统时间序列方法对复杂的非线性关系拟合性较差且无法添加与预测指标相关的变量,预测精度难以提高[2]。之后,学者们转向对非线性系统拟合较好的机器学习算法进行宏观经济预测。Wang&Shang(2014)、Wang等(2016)将改进SVM模型应用于证券与股票指数预测中,证明了改进支持向量机模型预测的有效性[3~4]。然而在经济领域数据之间普遍存在时序关系,机器学习算法不能较好地反映样本间的时序关系。随着机器学习领域中深度学习的研究和发展,其中的递归神经网络(RNN)适用于处理序列数据。但是由于RNN存在长期依赖问题,Hochreiter和Schmidhuber(1997)提出RNN的改进模型LSTM神经网络[5],并被Alex Graves等(2013)进行改良和推广,使LSTM得到更广泛的应用[6]。Fu等(2017)针对交通流的随机性和非线性特征,使用LSTM和门控循环单位(GRU)神经网络方法来预测短期交通流量,实验证明基于递归神经网络的LSTM和GRU模型表现优于ARIMA模型[7]。
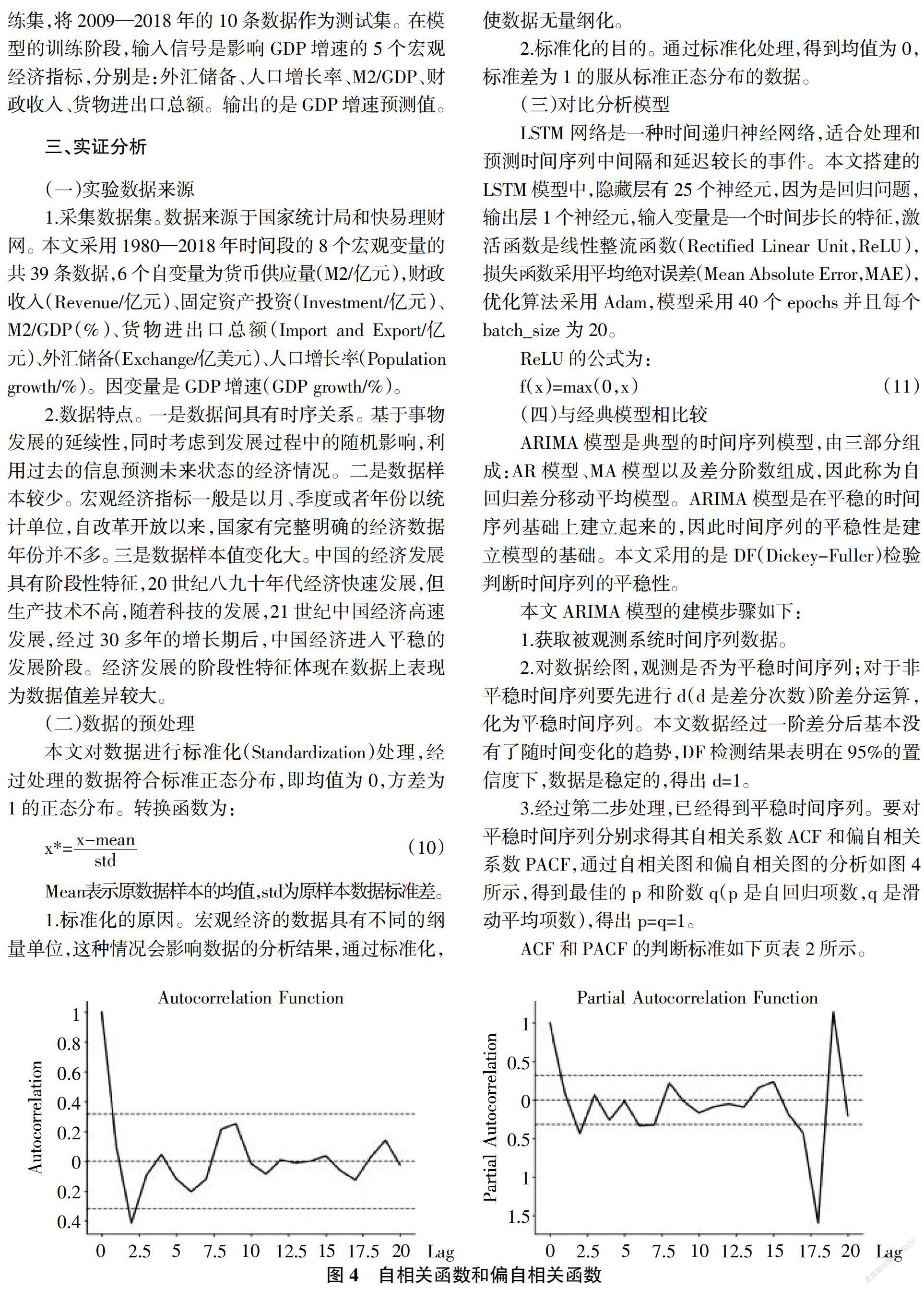
根据以上分析,本文主要是利用LSTM模型对中国宏观经济变量GDP增速进行预测分析。考虑影响经济的众多可能因素,在此分析过程中利用机器学习Random Forest算法提取影响经济发展的重要特征指标,通过LSTM算法对这些指标数据进行学习训练,对宏观经济进行预测分析。最后与时间序列预测模型(AR,MA,ARIMA)结果进行对比,可以看出LSTM算法在预测时序问题中具有精确高效性。
二、随机森林和LSTM预测模型
(一)随机森林评估特征的重要性
随机森林特征重要性评估能够辅助我们对特征进行筛选,从而使模型的鲁棒性更好。
特征重要性选择的目的:寻找与响应变量高度相关的重要变量,便于变量选择,使少数变量足以很好地预测响应变量[8]。
随机森林进行特征重要性评估的思想为:通过袋外(out-of-bag,OOB)数据误差增长百分率指标衡量特征重要性。
假设随机森林有N棵树,第K棵树的误差增长百分率如式(1):
其中,errOOBK1代表袋外数据误差,errOOBK2是对袋外数据对应变量加入噪声干扰或者改变样本在特征变量x处的值,再次计算得到的袋外数据误差。对于N棵决策树,如果加入随机干扰后,errOOBK2的值大幅上升,即误差增长百分率大幅上升,说明特征的重要程度比较高[9]。
随机森林根据特征重要性进行特征选择的步骤如下:
第一步,估计和排序。一是对随机森林的特征变量按照变量重要性(Variable Importance,VI)降序排序。二是确定删除比例,从当前的特征变量中删除相应比例不重要的指标,从而得到一个新的特征集。三是用新的特征集建立新的随机森林,并计算特征集中每个特征的VI并排序。四是重复以上步骤,直到剩下m个特征。
第二步,根据第一步得到的每个特征集和建立的随机森林,计算对应的袋外誤差率(OOBerr),将袋外误差率最低的特征集作为最后选定的特征集。本文收集的原始数据集中共包含8个变量,1个因变量和7个自变量。根据随机森林特征重要性排序,7个自变量的特征重要性排序如表1所示。从表1可以看出,第6、第7两个变量即货币供应量和固定资产投资,特征重要性比较低,故本文选取前5个变量作为模型的自变量,即人口增长率,M2/GDP,外汇储备,货物进出口总额,财政收入[10]。

