我国股票市场与债券市场的交互相关性分析
沈思敏
(南京财经大学 应用数学学院,江苏 南京210023)
0 引言
股票和债券是金融市场的两个重要资产类别,在投资组合中发挥着重要的作用.随着我国金融市场的蓬勃发展,单一市场内存在的系统性风险不断增加,仅扩充单一市场内的投资组合很难分散风险.因此,跨市场配置组合投资受到市场投资者的关注.研究股债市场之间的相关性,将有助于投资者完善投资组合策略,规避市场风险;有助于监管者制定相关政策,确保市场平稳健康发展.
基于分形市场理论可知,金融市场是一个具有分形和混沌结构的非线性动态复杂系统[1-5].这使得将一些常规的统计分析方法应用于市场分析时,可能产生较大偏差.因此,分形分析方法应运而生,其中,重标极差分析(Rescaled Range Analysis,简称R/S)方法与消除趋势波动分析(Detrended Fluctuation Analysis,简称DFA)方法属于单分形分析法,它们仅能对时间序列的整体特征进行描述,缺乏对序列局部特征的更细致的刻画.Kantelhardt[6]对DFA方法进行推广得到多重分形消除趋势波动分析(Multifractal Detrended Fluctuation Analysis,简称MF-DFA)方法,用于研究非平稳时间序列的波动特征和分形性质.目前,已有学者运用该方法发现加密货币、原油、股票和碳排放权等金融市场的价格波动具有多重分形特征[7-10].进一步地,MF-DFA方法被拓展为研究两个时间序列之间相关关系的多重分形消除趋势交互相关性分析(Multifractal Detrended Cross-Correlation Analysis,简称MF-DCCA)方法[11].现在,MF-DCCA方法已被广泛应用于研究不同市场间交互相关关系的多重分形特征.例如,李淑萍等[12]使用MF-DCCA方法研究中国股票市场、外汇市场、货币市场的交互相关关系,发现3个市场之间存在较强的交互相关性,且在小波动下表现出持续性特征,在大波动下表现出反持续性特征.张茂军等[13]运用MF-DCCA方法研究美国股债市场的交互相关关系,发现在小波动情形下,交互相关性表现为弱持续性,而在大波动情形下,交互相关性是反持续性的,并且突发事件会对相关关系产生影响.Ghazani等[14]采用MF-DCCA方法研究3种主要加密货币与一些知名原油市场之间的交互相关性,发现每对时间序列之间均具有显著的交互相关性.
近些年来,随着中国股票市场与债券市场的迅猛发展,两个市场之间的关系变得愈加紧密与复杂.为了更深入地了解两个市场之间相互关系的复杂特征,揭示跨市场投资组合的风险大小,本文以沪深300指数、上证国债指数与上证企债指数为研究对象,运用MF-DCCA等多重分形分析方法,实证研究我国股债市场间的交互相关性,寻找风险最小、收益最大的投资组合,为市场投资者与市场监管者提供科学有效的决策参考.
1 多重分形分析方法描述
MF-DCCA方法的算法步骤如下:给定两个长度均为N的时间序列
第3步:采用最小二乘法拟合这2Ns个子序列的局部趋势,分别得到X(i)和Y(i)在第v个子序列中的拟合多项式并利用其消除局部趋势,得到协方差:

第5步:如果两个序列之间存在幂律交互相关关系,则有下列关系式:

其中标度指数hxy(q)称为广义交互相关指数,它可用于描述两个时间序列之间交互关系的特征.
如果hxy(q)与q相关,表明两个序列之间的交互相关性是多重分形的,否则是单分形的.当hxy(q)>0.5时,两个序列之间的交互相关性是持续的,隐含着当一个序列增加(下降)时,另一个序列也随之增加(下降);当hxy(q)<0.5时,两个序列之间的交互相关性是反持续的,隐含着当一个序列增加(下降)时,另一个序列反而下降(增加);当hxy(q)=0.5时,表明两个序列之间没有交互相关性或至多短程交互相关.此外,对应于q的正负,hxy(q)分别描述小波动和大波动下的标度行为.
Shadkhoo等[15]给出两个交互相关序列的Renyi指数τxy(q)与hxy(q)之间的关系:τxy(q)=qhxy(q)-1.
如果τxy(q)对q是非线性的,则两个序列的交互相关性是多重分形的,否则是单分形的.通过Legendre变换,可以得到奇异指数α和多重分形谱fxy(α)的关系如下:
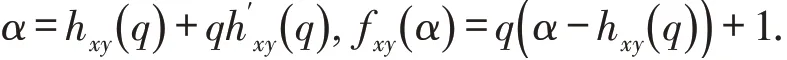
在MF-DCCA方法中,Δh=max(hxy(q))-min(hxy(q))能够描述两个序列之间交互关系的多重分形性强度.Δh越大,多重分形性越强,投资组合中隐含的金融风险就越大.另一方面,多重分形谱宽度Δα=αmax-αmin可以反映市场波动的大小,Δα越大,多重分形性越强,市场也就越动荡.
2 数据描述与统计检验
沪深300指数是沪深证券交易所联合发布的反映A股市场整体走势的指数,其样本覆盖沪深市场六成左右的市值,能充分反映我国股市的运行特征.上证国债指数和上证企债指数是我国债券市场的两个重要指标,能综合反映我国债市的整体水平.因此,本文选取沪深300指数、上证国债指数和上证企债指数的每日收盘价作为研究对象,样本区间为2009年8月3日至2020年3月2日,共2 571个数据(数据来源于http://money.163.com/).
图1 分别展示在样本区间内沪深300指数、上证国债指数和上证企债指数每日收盘价的波动形态.由图1可见,我国股市在2015年股灾发生时出现较大的波动.上证国债指数和上证企债指数每日收盘价走势基本一致,在样本区间内呈现一路上升的趋势,并且债市的两个指标在2015年前后并未出现较大的波动,这说明相较于股市,债市更稳定.

图1 沪深300指数、上证国债指数和上证企债指数每日收盘价走势
为了消除时间序列可能存在的异方差,需要对数据进行处理.利用公式ln(Pt+1/Pt)(Pt表示第t日的收盘指数),将3个时间序列转化为日对数收益率序列.图2给出这3个对数收益率图.从图2可见,3个收益率序列持续波动,并且十分剧烈,均表现出明显的波动聚集特征,并且股市的波动幅度显著地大于债市的波动幅度.

图2 沪深300指数、上证国债指数和上证企债指数的对数收益率
表1 给出3个收益率序列的描述性统计量.从表1可以看出,3个收益率序列的偏度不为0,表现为沪深300指数与上证国债指数收益率序列为左偏,上证企债指数收益率序列为右偏,三者的峰度均大于3,并且J-B统计量在1%的显著性水平下拒绝原假设,因此,这3个收益率序列均不服从正态分布,呈现出“尖峰胖尾”的特征.

表1 沪深300指数、上证国债指数和上证企债指数收益率序列的描述性统计量
下面运用Podobnik等[16]提出的交互相关性检验方法,检验3个收益率序列之间的交互相关性.给定两个时间序列x(i),y(i),i=1,2,…,N,定义交互相关函数和交互相关检验统计量为:
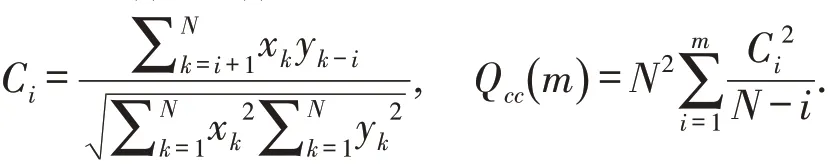
图3 给出3对指数,分别是沪深300-上证国债、沪深300-上证企债和上证国债-上证企债的交互相关检验统计量Qcc(m)的双对数图.为了方便对照,图3也给出卡方分布在5%的显著性水平下的临界值.从图3可知,3对收益率序列的交互相关检验统计量Qcc()m都比自由度为m的卡方分布的临界值大,表明3对收益率序列之间存在交互相关关系.

图3 Qcc(m)~m双对数图
3 交互相关性的多重分形分析
3.1 交互相关性的多重分形特征分析
下面运用MF-DCCA方法和多重分形谱分析法定量研究3个收益率序列之间交互相关性的多重分形特征与强度.
图4 绘制3对收益率序列的波动函数Fxy()q,s对时间标度s的双对数图.从图4可见,对于不同的q值,所有曲线在大标度下都基本呈线性关系,表明3个收益率序列之间均存在幂律交互相关关系.
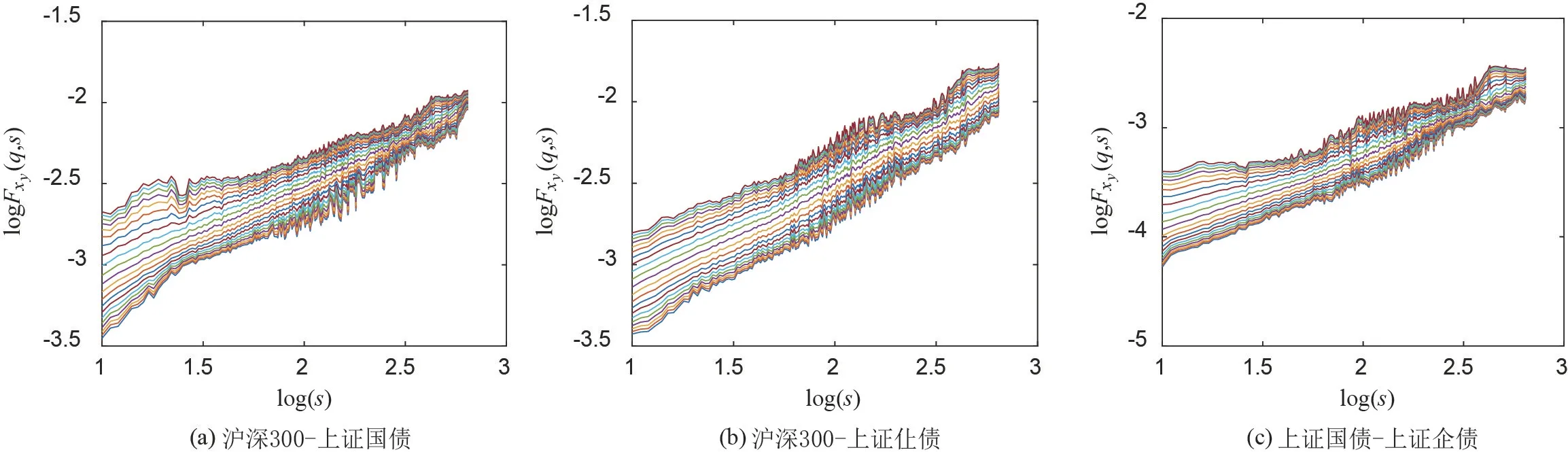
图4 3对收益率序列波动函数的双对数图
表2 给出3对收益率序列的交互相关指数hxy(q)对应q从-10到10的取值情况.从表2可见,所有hxy(q)的值均随q的增加而非线性减小,表明3个收益率序列之间的交互相关性是多重分形的.当q>5时,沪深300-上证国债的交互相关指数hxy(q)小于0.5,表明在大波动下,沪深300指数与上证国债指数之间的交互相关性是反持续性的.对所有q从-10到10,沪深300-上证企债和上证国债-上证企债的交互相关指数hxy(q)均大于0.5,表明这两对指数的交互相关性是持续性的.
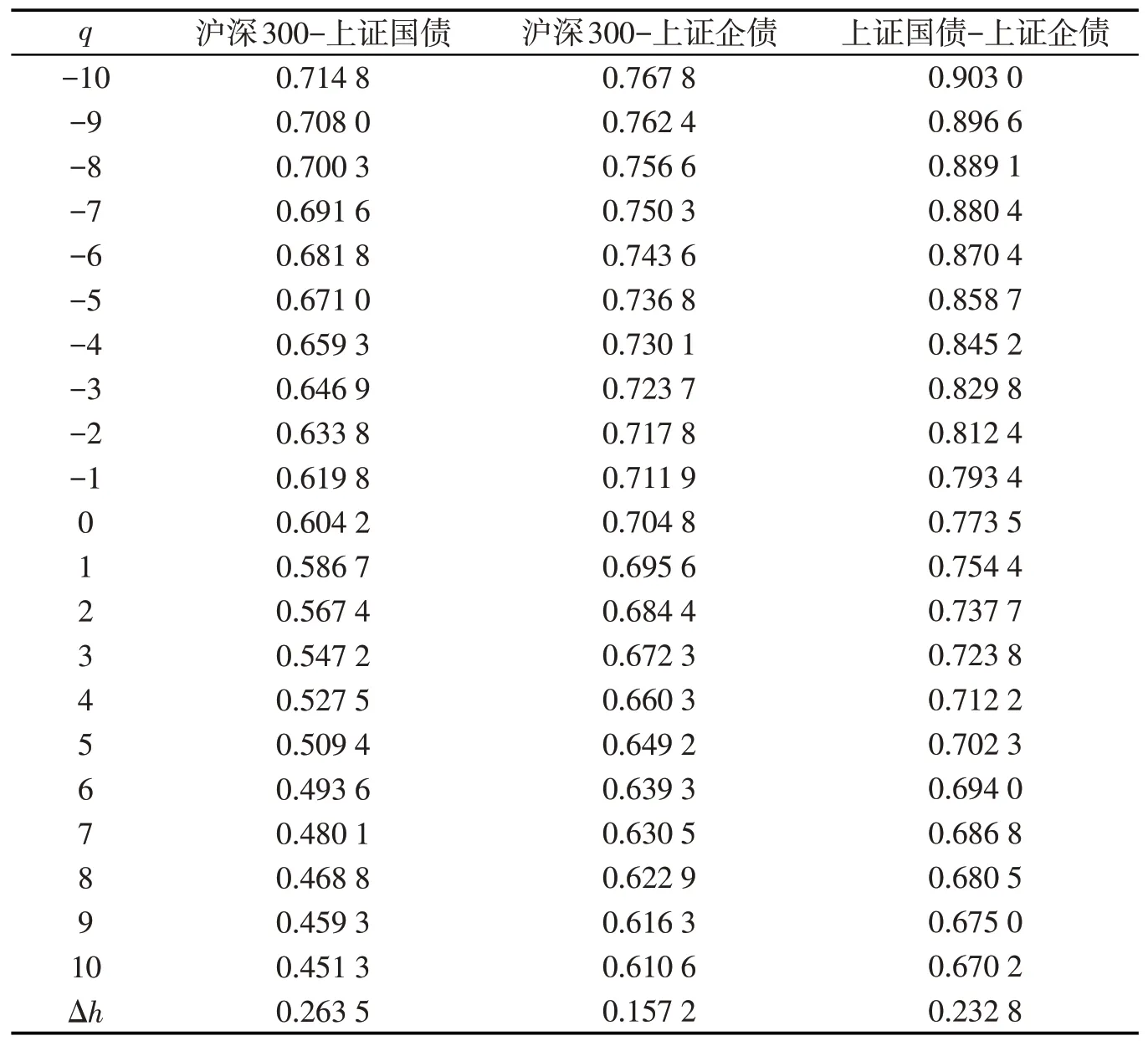
表2 3对收益率序列的交互相关指数hxy()q
观察3对收益率序列的多重分形强度Δh,沪深300-上证国债的多重分形强度Δh最大,表明沪深300指数与上证国债指数的收益率组合隐含的金融风险最大,上证国债-上证企债的次之,而沪深300-上证企债的多重分形强度Δh最小,表明股票与企债的投资组合最能规避风险.
图5 绘制3对收益率序列的交互相关指数hxy(q)对q的变化图.从图5可见,这些交互相关指数hxy(q)随q的增加而非线性减小,说明3个收益率序列之间的交互相关关系是多重分形的.这与从表2得到的结论相吻合.
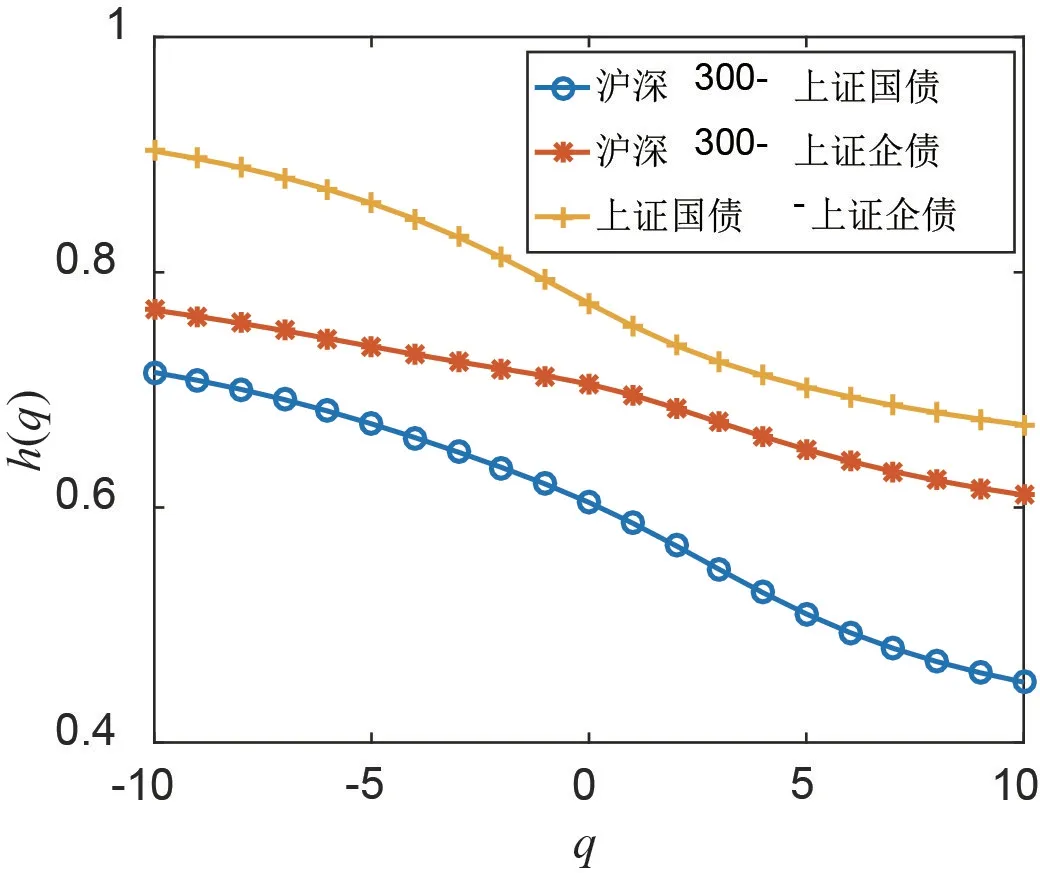
图5 3对收益率序列的hxy(q)~q图
图6 展示3对收益率序列的Renyi指数τxy(q)对q的变化图.从图6可见,这些Renyi指数τxy(q)随q的增加而非线性增加,进一步验证3个收益率序列之间的交互相关关系是多重分形的.此外,沪深300指数与上证国债指数的Renyi指数τxy(q)~q曲线的弯曲程度最大,进一步说明股票与国债的投资组合风险最大.
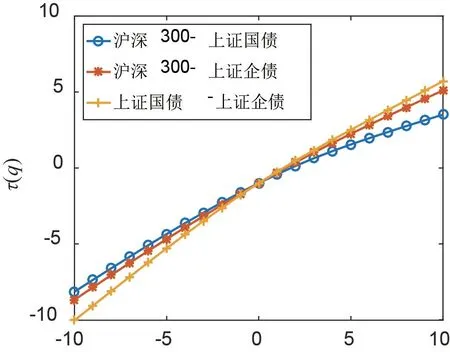
图6 3对收益率序列的τxy(q)~q图
图7 展示3对收益率序列的多重分形谱图.从图7可见,3对收益率序列的多重分形谱图呈现单钟峰形,也表明3个收益率序列之间的交互相关关系是多重分形的.表3给出这3对收益率序列的多重分形谱宽度Δα的值.从Δα的值来看,沪深300-上证国债的多重分形谱宽度最大,上证国债-上证企债的次之,沪深300-上证企债的多重分形谱宽度最小,这也说明股票与国债的投资组合风险最大,而股票与企债的投资组合风险最小,与前面得到的结论一致.
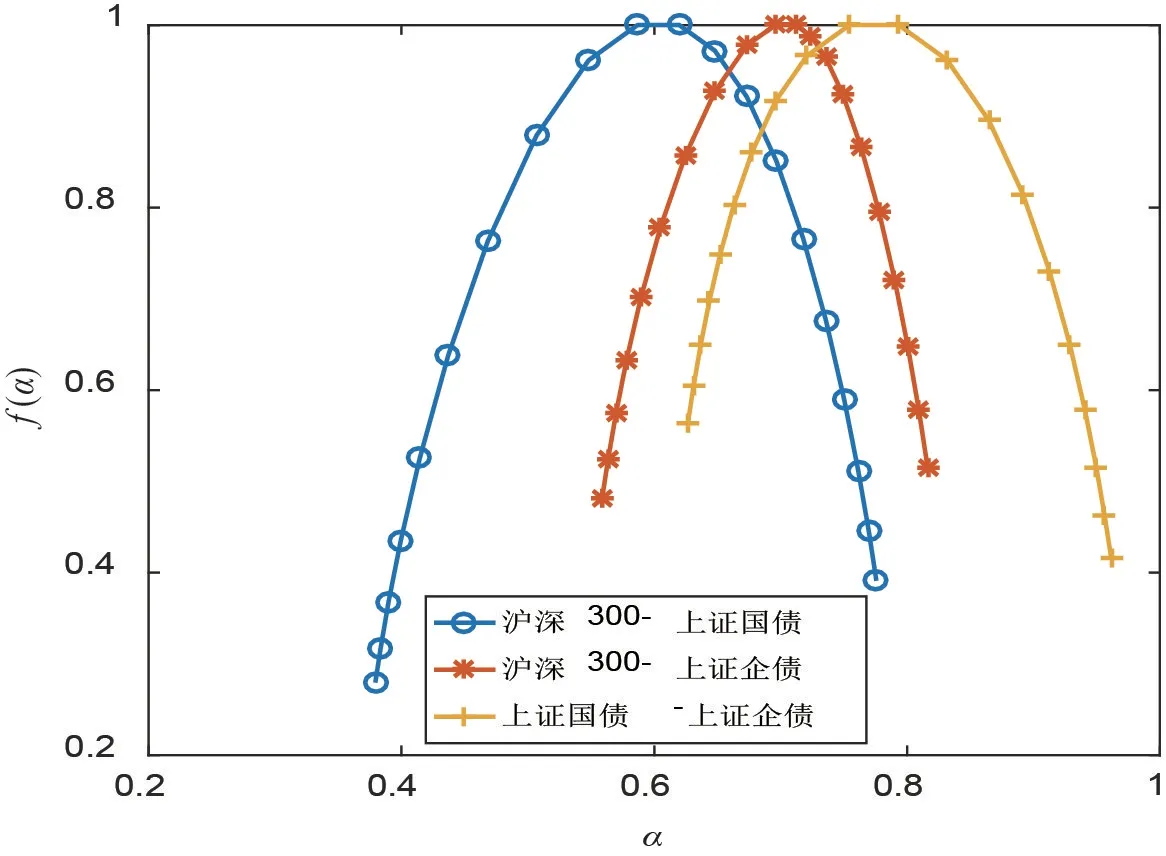
图7 3对收益率序列的多重分形谱图
3.2 多重分形性的成因分析
前面的分析已经证实3个收益率序列之间的交互相关关系具有多重分形特征.接下来,探究形成多重分形性的原因.现有的研究成果表明,形成多重分形性的原因主要有两个,即时间序列的长程相关性和胖尾分布[17].通过对比原始序列、打乱序列和替代序列的Δh和Δα的大小,可以检验长程相关性与胖尾分布对多重分形性形成的影响.
图8 和图9分别绘制3对收益率序列的原始序列、打乱序列和替代序列的广义交互相关指数hxy(q)~q图以及多重分形谱fxy(α)~α图.表4给出3对收益率序列的原始序列、打乱序列和替代序列的Δh和Δα的值.从图8、图9和表4可见,沪深300-上证国债的打乱序列的Δh和Δα比较接近于原始序列的Δh和Δα,而替代序列的Δh和Δα均明显小于原始序列的Δh和Δα,表明胖尾分布是沪深300指数与上证国债指数之间交互相关性具有多重分形性的主要原因.沪深300-上证企债和上证国债-上证企债这两对收益率序列的打乱序列和替代序列的Δh和Δα均与原始序列的Δh和Δα有较大差别,且替代序列的差别尤为显著,表明长程相关性和胖尾分布均是影响多重分形性的主要原因,而胖尾分布的贡献更大.

图8 3对收益率序列的原始序列、打乱序列和替代序列的hxy(q)~q图

图9 3对收益率序列的原始序列、打乱序列和替代序列的多重分形谱图

表4 3对收益率序列的原始序列、打乱序列和替代序列的Δh和Δα
4 结论与建议
本文研究沪深300指数、上证国债指数与上证企债指数的收益率序列之间的交互相关性.得到以下结论:首先,基于描述性统计量和交互相关统计量检验,发现3个收益率序列的分布呈现出“尖峰胖尾”的特征,并且3个收益率序列之间存在显著的交互相关性.其次,运用MF-DCCA方法和多重分形谱分析方法定量地研究3个收益率序列之间交互相关关系的复杂性特征,结果表明,3个收益率序列之间的交互相关关系具有多重分形性特征,并且沪深300指数与上证国债指数的组合收益率序列的多重分形性强度最大,沪深300指数与上证企债指数的组合收益率序列的多重分形性强度最小,表明股票与国债的投资组合风险最大,而股票与企债的投资组合风险最小.最后,对比3对收益率序列的原始序列、打乱序列与替代序列的Δh和Δα,发现胖尾分布是形成多重分形性的主导性因素.
基于以上结论,本文为我国市场监管部门与投资者提出以下几点建议:1)考虑到我国股票市场和债券市场之间的交互相关性具有多重分形特征,且胖尾分布是形成多重分形性的主导性因素,表明投资者通常以非线性方式对信息作出反应,即仅对累积到一定程度的信息进行处理,这容易导致投资者产生“羊群效应”等非理性行为,因此,投资者在进行组合配置时不仅要收集单个市场的价格波动信息,还要将我国股票、国债和企债市场纳入一个整体框架中,综合考虑3个市场中价格波动和风险传导效应对投资组合未来收益的影响,合理构建跨市场配置投资组合,分散单一市场内的风险.2)尽管股票与企债的投资组合风险最小,但投资者对企债市场兴趣寥寥,这是由于我国企债市场发展明显落后于国债等其他债券市场,且市场流通性差,发行品种单一等在很大程度上限制投资者的选择.因此,相关监管部门应当完善企债市场,加强市场流通性,吸引投资者的目光.3)市场监管者应进一步完善信息披露机制,降低信息的不对称性.同时,宏观把握金融子市场之间的相关关系,防范系统性金融风险,促进我国金融市场健康、稳定地运行.

