利率下行、长寿风险与商业养老年金风险评估

胥佩彤 南开大学金融学院

对长寿风险和利率风险的量化是商业养老年金定价、风险管理与偿付能力评估的基础。为评估养老年金的利率下行风险与长寿风险，本文采用微分重要性测度与情景对比法对终身养老年金负债现金流的精算现值进行敏感性分析，测度养老年金成本中长寿风险和利率风险的相对重要性，并量化风险规模。研究表明，在利率下行背景下，长寿风险对养老年金成本的负面效应有所加强；而在高利率水平下，长寿风险的相对重要性显著下降。此外，情景分析结果表明，利率因素和死亡率因素的交叉效应对养老年金负债水平影响显著。

一、引言

随着经济发展水平的提高和医疗技术的进步，我国人口整体预期寿命显著提升。但对于养老年金业务而言，投保人群整体性的死亡率改善将带来较大的系统性长寿风险，这意味着未来领取生存金人数的增多和领取期限的延长，给付总额将会不断提高，养老年金账户负债端将承受较大压力。未预期的长寿风险将导致保险公司定价时低估费率，极有可能引发偿付能力不足的风险。

与此同时，全球都在经历低利率甚至负利率时期，而我国则可能将在经济“新常态”下保持较长时间的低利率环境。养老年金产品一般期限较长，因而对利率的敏感性更高，当评估利率下降时，未来给付现金流的贴现值变大，养老年金产品的责任准备金将会显著上升。此外，在长期利率下行阶段，保险公司再投资风险升高，若此时年金预定利率高于实际投资回报率，养老年金业务就会出现较为严重的利差损问题。

当利率下行与长寿风险共存时，就会给养老年金产品的负债端带来双重考验。但是，究竟是利率风险还是长寿风险对养老年金负债端的负面影响更大，两种风险是否存在交互效应，又该如何量化利率风险和长寿风险？国内外学者对此进行了广泛讨论，结论也并不一致。Mahayni和Steuten（2011）研究了递延年金的系统性死亡率和利率风险，表明随机死亡率对年金的影响比随机利率小，且其风险主要源于与随机利率的相互作用。Haberman等（2011）将熵的概念引入年金成本的分析中，研究表明利率越低，熵值越大，长寿风险对年金给付现值的影响越大，在死亡率极高与极低的情景下，死亡率对年金成本的影响变小。Liu（2013）定义了年金率以表征年金的系统性风险，研究了随机利率和随机死亡率对年金率的相对影响，表明年金率对长期利率最敏感，但当利率处于低位时长寿风险将会变大。Karabey等（2014）使用Hoeffding分解和泰勒展开两种方法确定了利率风险和死亡率风险对年金价值的边际风险贡献。Rabitti等（2020）使用局部敏感性与全局敏感性分析法比较了利率和死亡率对年金的影响，表明人口因素是低利率背景下最重要的风险来源，而在考虑了两种风险的不确定性时，利率风险成为全局风险的主要驱动因素。国内文献方面，祝伟和陈秉正（2008）分析了使用新生命表对个人年金产品价格的影响，为从年金产品价格被低估的角度来衡量长寿风险提供了参考，研究表明，利率越低，长寿风险的负面效应越强。段白鸽（2019）研究发现，利率风险和长寿风险存在对冲，低利率情况下长寿风险更显著。

为了将利率下行风险与长寿风险对年金成本的负面影响进行量化和对比，本文基于Haberman等（2011）和Rabitti等（2020）的理论框架，采取微分重要性测度和情景对比法两种敏感性分析方法，测度死亡率和利率在影响养老年金负债端的相对重要性，并量化利率风险和死亡率风险分别对养老年金成本影响的方向和规模，以及两种风险共存的情况下对养老年金成本产生的交叉效应。

二、敏感性分析理论模型

（一）基于生命表的微分重要性测度

假设被保险人购买了连续终身年金，生存金的起付年龄为x岁，该年金在被保险人年满x岁后每年支付一个单位的生存金，直至被保险人死亡。假设仅考虑该养老年金的未来生存金给付现金流，不考虑退保、费用等因素，在被保险人年满x岁时该连续年金的负债现金流的精算现值āx为：

其中，δ表示连续复利情景下的利率，生存概率，代表x岁的被保险人活过t年的概率，μx代表被保险人x岁时死亡力。从式（1）中可以看出在相同年龄情况下，年金成本āx主要受利率δ和死亡力μx的影响。

假设死亡力μx变动φ个单位，被保险人在x岁的死亡力变为μx*=μx（1+φ），此时生存概率为：

假设δ变动λ个单位，即利率变为δ*=δ（1+λ）。此时，连续终身年金负债端现金流的精算现值为：

定义函数f(φ,λ)=μx*/āx以此衡量利率和死亡率改变后养老年金现值的相对变化水平。函数f(φ,λ)在点(0,0)处的一阶泰勒展开式为：

其中，

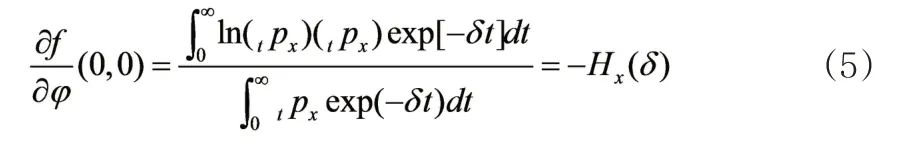
式（5）中Hx(δ)是Haberman等（2011）研究中年金成本的熵。熵值为正，用来衡量年金成本对死亡率的敏感程度。熵值越大，代表死亡率每改变一个单位将导致年金成本的变化幅度越大。Hx(δ)与利率δ呈反比关系，意味着随着利率的增加，熵值减小，年金成本对死亡率的敏感性变低，即高利率下，死亡率对年金成本的影响较小。

同样地，f(φ,λ)对λ求偏导，结果为：

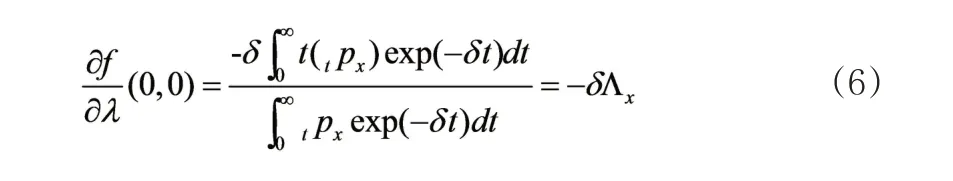
其中，Λx为Salinelli（1990）研究中年金产品的久期。

Rabitti等（2020）将f(φ,λ)分别对φ和λ求偏导的结果，构建微分重要性测度指标。如式（7）所示，死亡率风险因子φ和利率风险因子λ的微分重要性测度指标分别为Dφ和Dλ，该指标是将偏导数的梯度信息归一化后的比例：

分别代入式（5）和式（6），得到年金成本的微分重要性测度表达式为：

式（8）将熵值和久期有机结合起来，通过Dφ和Dλ的值就可以得出死亡率变化幅度φ和利率变化幅度λ的相对重要性水平，并据此对利率风险和长寿风险的重要性进行排序。

其中，ω为生命表中的最大年龄。式（6）中久期Λx的离散形式近似方法与此类似。

（二）基于Gompertz模型的情景对比法

假设死亡率服从Gompertz模型，即μx=exp(b+cx)。根据Haberman等（2011）的研究，引入死亡率随时间变化的动态特征，假设瞬时死亡率以exp(-αt)指数形式衰减下降，即。此时，生存概率为：

将式（10）代入终身连续年金负债现金流的表达式（1），得到：

为使生存概率不大于1，假设α＜c。

为研究式（11）中的各参数变化对养老年金成本的影响，使用情景对比法进行直观分析。以基础情景z0为基准，设定乐观情景z+和悲观情景z-的参数，使用控制变量法将基础情景下的参数逐个变更为其他情景中的参数，并与基础情景下的输出变量结果做对比，得到单因素变化对输出结果的影响。即输入变量变为和，将输出结果、与基础情景的结果g(z0)做差，就可以得到各因素对输出结果的影响幅度：

从基础情景转变为其他情景后，输出结果的总变化值记为Δg，将其拆解为：

其中，递推公式如下所示：

上式中，Δgi=1,2,...,n称为变量zi的主效应，其余高阶项称为交叉效应。

将式（13）中包含i的项目加总，得到变量zi对输出结果变化值Δg的总贡献ΔTgi：

变量zi的总交叉效应ΔIgi，可以通过zi的总效应ΔTgi与主效应Δgi作差得到：

三、实证分析

（一）微分重要性测度实证分析

1.数据来源与参数设定

基于《中国人寿保险业经验生命表（2000—2003）》中的养老金业务表（CL3-4）以及《中国人身保险业经验生命表（2010—2013）》的养老类业务表（CL5-6），计算不同年龄不同利率水平下养老年金的熵值。根据我国现阶段的法定退休年龄，将养老年金起付年龄x选取为45、50、55、60和65岁。根据当前行业寿险定价利率与评估利率，将年化利率选取为0.5%、1%、2.5%、3.5%和6%。

2.实证结果与解释

下面以男性养老年金的微分重要性测度结果为主进行分析。如表1所示，在固定利率水平下，随着年龄的增长，死亡率重要性测度值Dφ呈现递增趋势，意味着给付年龄越大，养老年金成本对死亡率的敏感性越高。由于Dφ和Dλ相加为1，因此利率因素和死亡率因素的相对重要性呈现此消彼长的动态关系，在Dφ增高时，Dλ逐渐降低，在起付年龄较高的情况下，养老年金对死亡率的敏感性相较于利率因素更高。因此，实证结果表明，在固定利率水平下，随着养老年金起付年龄的升高，长寿风险导致养老金成本上升的幅度会变大。

表1 基于CL3（2000—2003）的微分重要性测度

从横向结果对比来看，当起付年龄相同时，死亡率重要性呈现此消彼长的动态关系，在Dφ增高时，Dλ逐渐降低，在起付年随着利率的升高而降低，意味着在高利率水平下，利率改变引起的养老年金成本的变化远远大于死亡率带来的结果。反之，利率下降，死亡率重要性呈现此消彼长的动态关系，在Dφ增高时，Dλ逐渐降低，在起付年逐渐升高，养老年金成本对死亡率的敏感性逐渐变大。这表明，长寿风险对养老年金负债的负面效应在利率下行阶段得到加强，在低利率情况下，长寿风险导致养老金成本的增加幅度将变大。该结论与祝伟和陈秉正（2008）、Liu（2013）等的一致。

如表2所示，基于2010—2013版生命表的重要性测度结果验证了前述结论。此外，对比表1与表2后，可以看出2010—2013版生命表的死亡率重要性测度结果呈现此消彼长的动态关系，在Dφ增高时，Dλ逐渐降低，在起付年普遍高于2000—2003版生命表，表明在保持利率不变的情况下，与边际效用递减类似，死亡率改善会使年金成本对死亡率的敏感性下降。以60岁男性为例，在1%的利率水平下，尽管表2的重要性呈现此消彼长的动态关系，在Dφ增高时，Dλ逐渐降低，在起付年相较于表1有所下降，但Dφ仍然大于Dλ，表明在低利率和死亡率改善并存的情况下，总体上仍呈现长寿风险重要性的增加。

表2 基于CL5（2010—2013）的微分重要性测度

前述规律与女性生命表计算的结果一致，故在此不作展示。由于女性整体的死亡率低于男性，导致计算出来的死亡率重要性测度Dφ值整体低于男性，Dλ值整体高于男性，表明女性养老年金对长寿风险的敏感性相较于男性偏低。

（二）情景对比法实证分析

1.数据来源

本部分采用2020年《中国人口和就业统计年鉴》中全国分性别、年龄死亡人口的数据进行情景对比法下的敏感性分析。该数据为2018年11月1日至2019年10月31日全国人口抽样调查统计结果，包含了男性和女性0—89岁各个年龄以及90岁及以上的年平均人口数和死亡人口数。

2.Gompertz模型拟合结果

使用Gompertz模型对45—89岁人群的死亡力进行拟合。分别将男性和女性的年平均人口数作为暴露数Ex，各年龄的死亡人口数记为dx，计算出各年龄下的死亡力μx=dx/Ex。将μx对数化，并关于年龄作线性回归，拟合结果如图1和图2所示。

图1与图2的横轴为年龄，纵轴为对数死亡力，散点为观测数据，直线为Gompertz模型的拟合结果。从图中可以看出，Gompertz模型对60—89岁人群的死亡率拟合效果较好，因此下文计算终身年金成本时，死亡率使用该拟合结果。此外，为简化分析，本文使用Gompertz模型外推90岁及以上的超高龄人群的死亡率，这与真实情况可能会存在一定偏差。

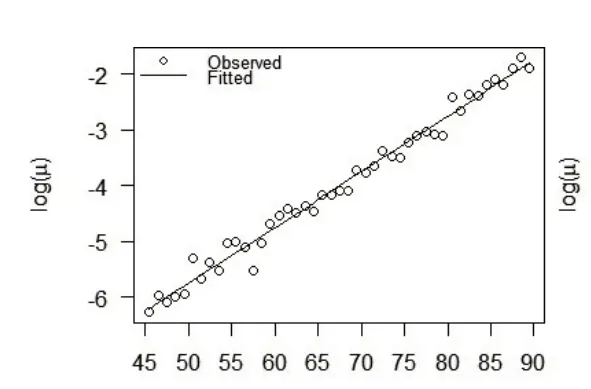
图1 男性Gompertz模型拟合效果

图2 女性Gompertz模型拟合效果

3.参数设置与情景选择

为设定乐观情景和悲观情景的参数，首先设置b、c、α、δ的变动范围。以Gompertz模型的拟合结果作为基础情景下的b、c值，Gompertz模型的参数估计结果如表3所示。设b的变动范围为上下变动10%，即上限为0.9b，下限为1.1b；c的变动上下限为±0.005；死亡率改善因子α的变动范围为（-0.07,0.07）；利率δ的变动范围为（0,0.1）。各参数的变动范围汇总结果如表3所示。

表3 Gompertz模型拟合结果与参数变动范围

依据Rabitti等（2020）的研究成果，选定男性被保险人的基础情景为：

乐观情景下，

悲观情景下，

女性被保险人基础情景的参数设置为：

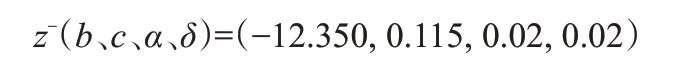
乐观情景下，

悲观情景下，

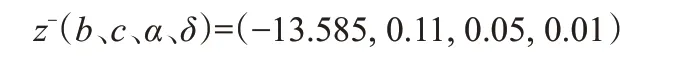
4.情景对比结果

假设终身养老年金的起付年龄为60岁，根据式（11），计算不同参数下的年金负债现值āx（b、c、α、δ），通过与基础情景成本的对比结果来判定乐观情景和悲观情景。乐观情景下的死亡率和利率高于基础情景，养老年金成本变低，而悲观情景下的死亡率和利率均低于基础情景，成本变高。以男性为例，男性基础情景下的养老年金负债的精算现值为18.217，乐观情景参数下得到的养老年金成本为7.213，悲观情景下为41.985。根据式（12）至（16），将乐观情景和悲观情景下各参数对养老年金成本的主效应、总效应和交叉效应进行拆分，结果如图3和图4所示。

图3 男性情景对比法变化情况

图4 女性情景对比法变化情况

图中横轴代表养老年金成本的变化值，纵轴代表两种情景下b、c、α、δ四个变量对应的主效应Δgi、总效应ΔTgi和交叉效应ΔIgi，正负号分别代表乐观情景和悲观情景，柱状图的方向和长度显示了b、c、α、δ引致的养老年金成本的变化值。

如图3所示，乐观情景下参数b、δ的主效应Δgi+最高，当b的绝对值下降10%时，男性养老年金成本下降6.15，当利率δ上升为0.05时，养老年金成本下降5.28；从总效应来看，b是最重要的因素，参数b带来的总效应约为-3，其次是利率δ；从交叉效应ΔTgi+来看，b、c、α、δ四个因素在积极情景下的交叉效应均为正值，即死亡率因素和利率因素对养老年金成本共同作用的结果是提高了年金成本，利率δ的交叉效应最高，其次为b和死亡率改善因子α。悲观情景下，b的主效应最高，其次为α和δ；总效应和交叉效应与乐观情景下的重要性排序情况相同。图4中女性的情景对比结果与男性基本相同，对年金成本影响较大的是和α。从情景对比法的实证结果来看，利率因素和死亡率因素对年金成本的交叉效应对养老年金成本的负面影响显著。

四、结论与不足

本文使用微分重要性测度法和情景对比法对影响养老年金成本的死亡率风险和利率风险进行了敏感性分析。在微分重要性测度模型下，运用Haberman等（2011）和Rabitti等（2020）的理论框架，将年金久期与熵值结合，并基于2000—2003年和2010—2013年我国人身保险业两套经验生命表进行计算，得到不同年龄及不同利率水平下的死亡率和利率风险因素的重要性测度指标。实证分析表明，在低利率的背景下，长寿风险会导致养老年金成本的上升幅度更为显著；随着生存金起付年龄的增长，长寿风险逐渐增强；随着死亡率的改善，年金成本对长寿风险的敏感性逐渐降低。

在基于情景对比法的敏感性分析中，本文采用Gompertz模型对老年人口的死亡率进行了拟合，并将拟合结果作为基础情景下的参数，接着把死亡率参数和利率参数对养老年金成本的主效应、总效应和交叉效应进行了拆解计算，最后通过图形展示了不同情景下养老年金成本相对于基础情景的变化情况。结果表明，利率因素和死亡率改善因素均会对年金成本有较大影响，同时，死亡率和利率的交叉效应对年金成本的负面影响显著。

综上所述，保险公司对养老年金系统进行风险评估时，需要综合考虑利率变化和死亡率改善的情况，将长寿风险和利率下行的负面效应有机整合，重视利率因素和死亡率因素的交叉效应。本文的不足之处有：使用的两种敏感性分析方法为局部敏感性分析法，输入变量有限；利率采用的是固定利率期限结构，未考虑利率和死亡率等风险因素的不确定性；情景对比分析法下使用Gompertz模型对超高龄人口的死亡率外推这一做法并不精确等。