系统可靠性分析方法与比较研究
张伟,贾瑶
(中国电子科技集团公司第三十六研究所,嘉兴 314033)
前言
系统工程中关于系统的定义为,是由相互联系、相互作用的许多要素组成的具有特定功能的复合体。系统整体与构成系统的部分是相对而言的,整体中的某些部分可以看成是该系统的子系统,而整个系统又可以成为一个更大规模系统中的一个组成部分或者子系统[1]。
所谓“系统可靠性”主要区别于一般的元器件、零部件和组件模块的可靠性,它的研究对象是整个系统。系统可靠性分析方法又有区别于眼下比较流行的失效物理(Physics of Failure,PoF)法,失效物理研究方法是基于产品失效的实际物理过程,通过探究产品失效模式与失效根因,从而构建相应的失效物理模型,达到对于产品失效的定量化描述和评价的目的。显然,失效物理研究方法不适用于系统可靠性评价问题,系统可靠性评价的核心目的在于达成针对对象产品的量化评价要求,即在数值上合理确定并最终给出对象产品的可靠性量化指标或称可靠性特征量。
不同的系统,不同的应用场合具有不同的可靠性分析手段,但研究系统可靠性的方法不外乎以下几种,分别是可靠性框图(RBD)法、故障树分析(FTA)法、Markov分析法、Monte-Carlo仿真、GO法和Petri网等方法。本文以这六种系统可靠性分析方法为基础,从方法的研究背景、原理、适用范围出发,阐述所谓“系统可靠性”分析方法的基本内涵与特征,在此基础上,针对不同分析方法的特点,结合工程实践与应用需求,对各种分析方法做了比较研究,研究结论供广大工程人员在做系统可靠性分析选择时参考。
1 系统可靠性分析方法
1.1 可靠性框图
可靠性框图法为各种系统可靠性分析方法中最简单的方法,但也是使用最为广泛的方法。可靠性框图是用方框表示系统各组成部分的故障或它们的组合如何导致产品故障的逻辑关系图,它描述了系统各组成部分之间的可靠性关系,并能够给出一个确切的数学表达式。典型的系统可靠性框图有:串联系统、并联系统、表决系统、旁联系统和网络系统。可靠性框图的研究基础是概率论,适用场合为不可修系统。下面简单描述以上几种典型的系统可靠性框图及其数学表达形式[2]。
1)串联系统
组成系统的所有单元中任一单元的故障都会导致整个系统的故障称为串联系统。
其逻辑框图(RBD)如图1所示。

图1 串联模型
其数学模型为:

式中:
Rs(t)—系统可靠度;
Ri(t)—第i个单元的可靠度。
2)并联系统
组成系统的所有单元都发生故障时,系统才发生故障称为并联系统,并联系统是最简单的冗余系统(热储备)。
其RBD如图2所示。
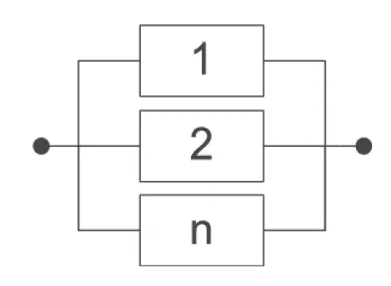
图2 并联模型
其数学模型为:

式中:
Rs(t)—系统可靠度;
Ri(t)—第i个单元的可靠度。
3)表决系统
组成系统的n个单元中,正常的单元数不小于r(1≤r≤n)系统就不会故障,这样的系统称为r/n(G)表决模型。
其RBD如图3所示。
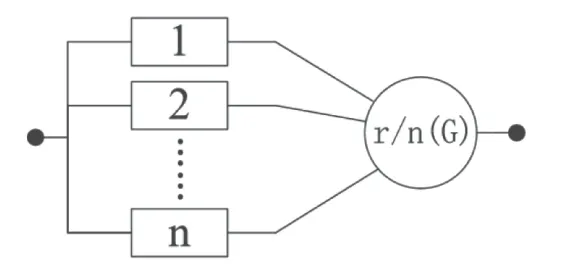
图3 表决模型
其数学模型为:
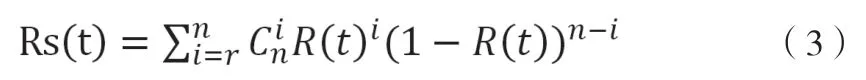
式中:
Rs(t)—系统可靠度;
R (t)—单元可靠度。
4)旁联系统
组成系统的各单元只有一个单元工作,当工作单元故障时,通过转换装置接到另一个单元继续工作,直到所有单元都故障时系统才故障,称为旁联系统,又称非工作贮备(冷备)系统。
其RBD如图4所示。

图4 旁联模型
其数学模型为:
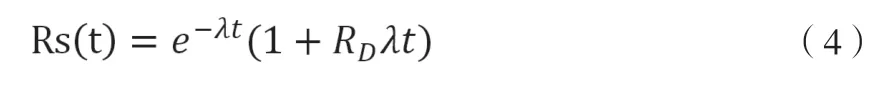
式中:
Rs(t)—系统可靠度;
RD—转换装置可靠度;
λ—第i个单元的故障率。
5)网络系统
网络系统为上述几种系统的组合,系统某些功能冗余形式或替代工作方式的实现,是一种既非串联也非并联的桥形式,称为桥联系统或网络系统。其数学模型的建立较为复杂且有个性,不能建立通用的表达式,具体情况需要具体去分析。
1.2 故障树分析
故障树分析(Fault tree analysis,FTA)是以一个不希望发生的产品故障事件或灾难性危险事件作为顶事件,通过由上向下的严格层次的故障因果逻辑分析,找到导致顶事件发生的所有原因和原因组合的逻辑因果关系图。FTA不仅能够对系统进行定性风险分析,在有基础数据时还可以进行定量分析计算,估计系统顶事件发生概率以及底事件的重要度。
FTA的核心在于寻找故障树的最小割集,所谓的最小割集是指导致顶事件发生故障的底事件组合,且缺少这个组合中的任一底事件都将不能导致系统故障。
FTA一般有3个步骤[2]:
第一步:建立故障树。确定分析目的、明确系统定义和故障判据,利用专用的事件和逻辑门符号,将系统中故障事件之间的逻辑关系表达出来,形成故障树。
第二步:规范故障树。将建立的故障树规范化,形成仅含有底事件、结果事件和与、或、非三种逻辑门的故障树,并将故障事件用字母代替予以简化。
第三步:分析与建议。根据建立的故障树,求得故障树的割集和最小割集,进行定性分析和定量计算。根据分析结果确定系统薄弱环节并提出相应的改进措施。
1.3 Markov分析
Markov分析将系统看做由多种状态构成,属于状态图State Diagrams的一种,具有两种状态,即工作状态和故障状态。系统从一种状态到另一种状态的转移概率仅与系统的当前状态相关,而与系统先前的状态无关,称之为Markov过程。
对于一个由N个相同单元组成的并联系统,可以确定N+1种状态,其中状态N表示所有N个单元均可正常工作,状态N-1表示有一个单元故障处于维修状态,而其它N-1个单元可正常工作,……,状态1则表示只有一个单元处于工作状态,而其它N-1个单元中的一个或多个处于维修状态,状态0表明系统中所有的单元均故障,即整个系统处于故障状态。应用Markov分析的一般过程为[3]:
第一步:确定系统所有存在的状态。
第二步:在仅考虑传输率的情况下确定系统在t时刻处于每种状态的概率,并给出用于描述系统整体状态的不同方程。
第三步:求解系统不同的方程,并定义系统的可靠度为:

式中:
R0(t)—系统在t时刻故障的概率;
λ和μ—系统中单元的故障率和维修率,一般均为常数,如果不是常数时将会变成半Markov过程或非Markov过程,其应用求解将会更为复杂。
对于给定的系统,通常有3种方法用于求解并可得到3种不同的方程,即系统状态分析方法、状态传输矩阵以及Markov图方法。这些方法在大量的教程和文献中已有系统详细的论述,本文不再赘述。
1.4 Monte-Carlo仿真
在大多数情况下,由于方程求解的难度很难得到一个精确的解析解时,Monte-Carlo是一种很好的解决方法。
Monte-Carlo方法是一种以概率和数理统计理论为基础, 通过随机变量的统计试验,随机模拟来求解数学物理、工程技术问题的近似解的数学方法。根据求解问题的不同,这里的随机变量主要有两类,即一类是影响系统性能的参数,另一类是系统各组成部分(部件或组件)的可靠性参数(如失效率、可靠度等)。
第一类随机变量主要用于那些性能难以用解析形式来表达,或者只能需要通过大量的试验结果对其性能进行评估的问题,并且组成该系统的部件或组件的性能可以随机变量的形式来表示的复杂系统。
对于这类问题的求解,首先需要确定那些所有可能影响系统性能的参数,并确定相应的随机变量及其分布。然后通过随机产生的性能参数来确定系统的性能,并与性能参数要求进行比对,按事先确定的失效判据来确定系统的故障与否,即若性能参数超标则计系统故障发生一次,最后可以确定系统的可靠度为:

由于Monte-Carlo方法以大数定理为基本原则之一,故仿真的次数越多,其预计或评估的结果越真实,利用Monte-Carlo方法分析系统可靠性的基本流程如图5所示[4]。
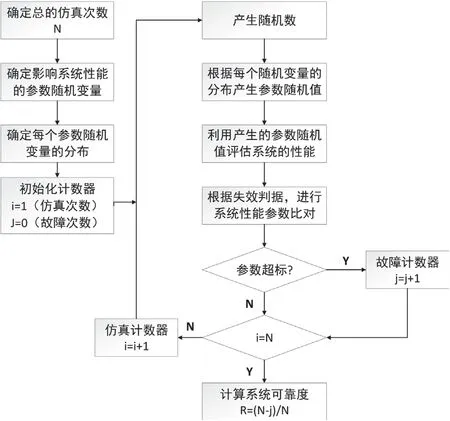
图5 Monte-Carlo仿真的基本流程图
对于复杂的电子产品而言,就可以考虑利用Monte-Carlo方法,在产品电路基础上对其功能进行仿真,来评估或预计电子产品的系统可靠性。
第二类随机变量主要用于那些已知系统各组成部分的可靠性特征量,并且可以给出该系统的可靠性框图或故障树的情况。但由于系统的可靠性模型过于复杂,难于推导出一个可以求解的通用公式时,Monte-Carlo方法可根据单元完成任务的概率,直接通过可靠性框图或故障树的近似计算来预计系统的可靠度。
1.5 GO法
GO法的基本思想是在20世纪60年代中期由美国Kaman科学公司最先提出,经过应用中不断完善,20世纪80年代以后在核领域得到了应用,是一种用图形演绎法来分析系统可靠性的方法。
GO法以成功为导向,运用操作符与信号流将系统的原理图或工程图直接翻译成GO图,并且用GO法程序计算所分析系统的各种状态的发生概率,用于评估系统的可靠度或可用度。
运用GO法进行系统可靠性分析的一般过程为[5]:
第一步:定义系统与边界。定义系统,确定系统的范围,明确系统中所有的可修单元和单元组成的系统结构,并给出系统的原理图或工程图。确定系统的输入边界与输出边界,确定系统、子系统和元件之间的接口关系。
第二步:建立GO图。根据系统工作原理图或工程图,用操作符表示系统的功能或部件,GO法中共定义了17种操作符。用信号流连接各个操作符,表示系统中各部件逻辑上的关系,最后生成GO图,用于系统的定性分析与定量评价。
第三步:进行GO运算。输入的系统单元可靠性参数(通常为故障率和平均修复时间MTTR), 根据GO法的运算规则,从输入操作符的输出信号开始,逐步运算至系统的输出信号,最终得到各个单元和系统的可靠性特征量。
1.6 Petri网
Petri网最早是由联邦德国的Carl Adam Petri于1962年在他的博士论文中提出,通过建立网状结构来模拟通信系统。Petri网是研究系统的一种工具,用来揭示出被模拟的系统在结构和动态行为方面的重要信息。Petri网既能图形化建模也可以进行数学计算,理论基础是系统各种状态及其动态变化之间的相互联系。Petri网是一种特殊的有向网,可用于描述复杂系统的静态和动态变化,直观的反映了系统状态变化和事件发展的过程[6]。
Petri网由三种类型的对象组成:库所(圆圈)、变迁(矩形)和有向弧(箭头)。连接库所与变迁之间的有向弧表示输入输出函数,用黑点或数字来表示标识以显示库所中资源的数量。库所中标识的数目决定变迁的使能和激发,变迁的激发又将改变库所中标识的数目,变迁的激发使得标识在库所之间流动[7]。因此,Petri网常用于描述系统动态的变化过程,能够直观的反映系统的动态特性。
在系统可靠性分析中Petri网尤其适合描述故障传播的过程,推断故障发生的原因,因此常用于故障诊断的场合,此外Petri网在可修系统的可靠性建模与分析、冗余系统的可靠性分析等方面也有广泛的应用。
2 系统可靠性指标
系统可靠性量化评价必然要输出可靠性指标,对于不可修系统,通常选用的系统可靠性指标为系统可靠度R、系统失效率λ、系统平均故障前时间MTTF(Mean Time To Failure,MTTF)。对于可修系统,通常选用的系统可靠性指标为系统可用度Ai、单元工作失效率λ与修复率μ、平均故障间隔时间MTBF(Mean Time Between Failure,MTBF)和平均故障修复时间MTTR(Mean Time To Repair,MTTR)。其中系统固有可用度Ai与其余可靠性指标参数的关系为[8]:
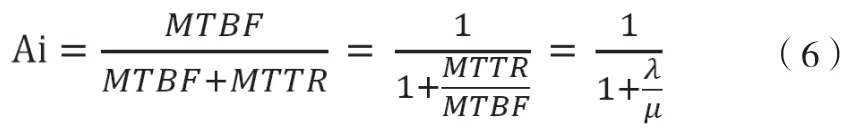
对于可修系统,不但要求使用期间具有很高的可靠性,同时还要求在使用以前能够保持很高的可用能力,因此,在满足系统高可靠性的前提下,还因适当降低系统的维修时间,以保持系统足够的可用度。
3 比较研究
本文重点介绍了六种系统可靠性分析方法,包括可靠性框图法、故障树分析、Markov分析、Monte-Carlo仿真、GO法和Petri网。基于这六种系统可靠性分析方法的特点,分别从其适用范围、输入条件、输出结果以及优缺点等几个维度进行比较,比较结果如表1所示,研究结论供广大工程人员在做系统可靠性分析时选择。

表1 系统可靠性分析方法比较
4 结语
系统可靠性分析需要建立相应的系统可靠性模型,而系统可靠性模型一般分为两类,即解析模型和仿真模型,而解析模型又可细分为网络模型和Markov模型。
其中网络模型由简单的可靠性框图或故障树组成。系统可靠性分析的输出结果(指量化结果)一般为通常所说的可靠性指标,系统可靠性指标一般用系统可用度进行评价,系统可用度综合反映了系统的可靠性与系统的维修性水平。
本文介绍了六种常见的应用于系统可靠性分析的方法,对六种方法从原理、适用范围及工作流程分别进行了简要的阐述分析,并对各种不同的系统可靠性方法分别从不同的维度进行比较研究,给出其适用的范围、输入与输出和优缺点分析,以便于在工程实际应用时进行选择参考。

